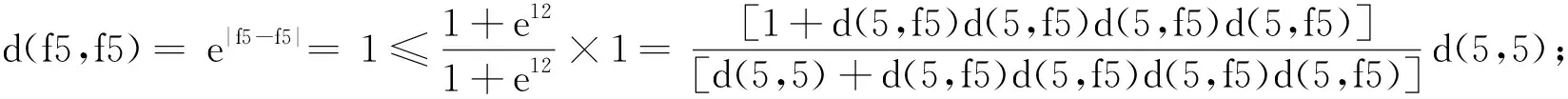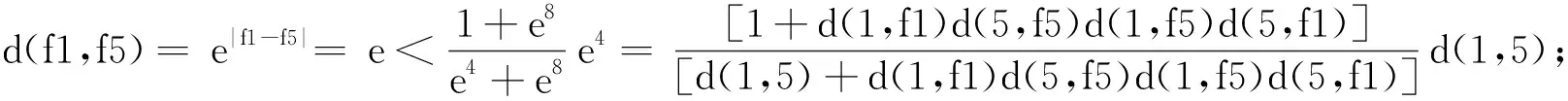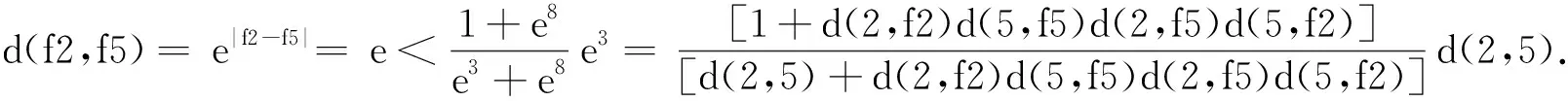乘积度量空间上的F-拟压缩条件和唯一不动点

朴勇杰

(延边大学 理学院 数学系, 吉林 延吉 133002)

设(X,d)是度量空间,f:X→X是自映射，则存在k∈[0,1)且使得对任意的x,y∈X始终有d(fx,fy)≤kmax{d(x,y),d(x,fx),d(y,fy),d(x,fy),d(y,fx)}成立.

在本文中，首先引进了一个五元函数类F， 并在完备的乘积度量空间上定义了F-拟压缩的概念；然后采用文献[20]中的证明思路证明了满足F-拟压缩条件的映射必有唯一不动点,并导出若干个推论，同时还通过实例验证了所得结果的正确性.

定义1[10]设X是非空集合，称映射d:X×X→[1,+∞)是X上的乘积度量是指d满足:

(ii)对任意的x,y∈X,d(x,y)=d(y,x)；

(iii)对任意的x,y,z∈X,d(x,z)≤d(x,y)d(y,z).

如果X和d满足上述条件，则称(X,d)为乘积度量空间.

定义2[10]设(X,d)是乘积度量空间, {xn}是X中的序列且x∈X.若对任何ε>1, 存在自然数N， 使得当n>N时有xn∈Bε(x)≜{y∈X|d(x,y)<ε}, 则称序列{xn}乘积收敛于x, 并记为xn→x(n→∞).

引理1[13]如果(X,d)是乘积度量空间, {xn}是X中的序列且x∈X，则有

定义3[13]设(X,d)是乘积度量空间， {xn}是X中的序列.若对任何ε>1， 存在自然数N， 使得当m,n>N时d(xm,xn)<ε始终成立，则称序列{xn}为乘积柯西序列.

引理2[13]如果(X,d)是乘积度量空间， {xn}是X中的序列，则{xn}是乘积柯西序列当且仅当d(xm,xn)→1 (m,n→∞).

定义4[13]如果乘积度量空间(X,d)中的每个乘积柯西序列都是乘积收敛的,则称(X,d)是完备的.

引理3[13]如果(X,d)是乘积度量空间, {xn}和{yn}是X中的2个序列且x,y∈X， 则有

xn→x(n→∞)且yn→y(n→∞) ⟹d(xn,yn)→d(x,y) (n→∞).

定义5函数类F为Φ∈F当且仅当Φ:[1,+∞)5→[1,+∞)满足:

Φ(i)Φ是连续且单调递增的;

Φ(ii) 当x≤Φ(x,x,x,x2,1)或x≤Φ(x,1,1,x,x)时，x=1.

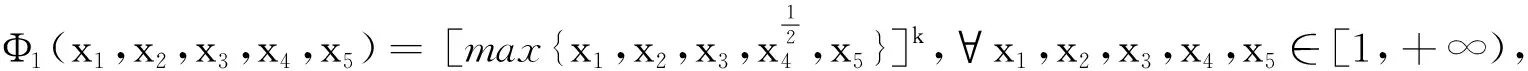
定义6设(X,d)是完备的乘积度量空间,f:X→X为自映射,则称f是F-拟压缩映射是指存在Φ∈F使得对任意的x,y∈X总有下式成立：

d(fx,fy)≤Φ(d(x,y),d(x,fx),d(y,fy),d(x,fy),d(y,fx)).

(1)

定理1设(X,d)是完备的乘积度量空间.如果f:X→X是F-拟压缩的,则f有唯一不动点,并且对任意的x∈X, 迭代序列{fnx}收敛于该唯一不动点.

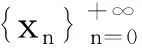
d(xn,xn +1)=d(fxn -1,fxn)≤

Φ(d(xn -1,xn),d(xn -1,fxn -1),d(xn,fxn),d(xn -1,fxn),d(xn,fxn -1))=

Φ(d(xn -1,xn),d(xn -1,xn),d(xn,xn +1),d(xn -1,xn +1),d(xn,xn))≤

Φ(d(xn -1,xn),d(xn -1,xn),d(xn,xn +1),d(xn -1,xn)d(xn,xn +1),1)).

(2)

如果存在某自然数N使得d(xN -1,xN)1.另一方面,根据式(2)的第1行和第4行以及条件Φ(i)和上述假设可得：

d(xN,xN +1)≤Φ(d(xN -1,xN),d(xN -1,xN),d(xN,xN +1),d(xN -1,xN)d(xN,xN +1),1))≤

Φ(d(xN,xN +1),d(xN,xN +1),d(xN,xN +1),[d(xN,xN +1)]2,1)).

再根据条件Φ(ii)可得d(xN,xN +1)=1, 这与d(xN,xN +1)>1相矛盾，因此必有

d(xn,xn +1)≤d(xn -1,xn),∀n=1,2,….

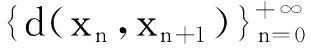
(3)

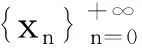
d(xm(k),xn(k))>ε,d(xm(k) -1,xn(k))≤ε.

(4)

由式(4)和定义1可得:

ε

对上式两边取k→ +∞并再利用式(3)可得:

(5)

于是根据定义1可得:

(6)

(7)

在式(6)和式(7)两边取k→ +∞并再根据式(3)和式(5)可得:

(8)

类似地,根据式(3)和式(8),对式

的两边取k→ +∞可得:

(9)

根据式(1)可知，对任意的自然数k有下式成立:

d(xm(k) +1,xn(k) +1)=d(fxm(k),fxn(k))≤

Φ(d(xm(k),xn(k)),d(xm(k),fxm(k)),d(xn(k),fxn(k)),d(xm(k),fxn(k)),d(xn(k),fxm(k)))=

Φ(d(xm(k),xn(k)),d(xm(k),xm(k) +1),d(xn(k),xn(k) +1),d(xm(k),xn(k) +1),d(xn(k),xm(k) +1)).

根据式(1)可知，对任意的自然数n有下式成立：

d(xn +1,fx*)=d(fxn,fx*)≤

Φ(d(xn,x*),d(xn,fxn),d(x*,fx*),d(xn,fx*),d(x*,fxn))≤

Φ(d(xn,x*),d(xn,xn +1),d(x*,fx*),d(xn,fx*),d(x*,xn +1)).

对上式取n→ +∞, 并再根据条件Φ(i)、引理2、引理3及定义1可得：d(x*,fx*)≤Φ(1,1,d(x*,fx*),d(x*,fx*),1)≤Φ(d(x*,fx*),d(x*,fx*),d(x*,fx*),[d(x*,fx*)]2,1).由此再根据条件Φ(ii)可得d(x*,fx*)=1, 因此x*是f的一个不动点.

如果y*∈X也是f的不动点,则由式(1)可得：

d(x*,y*)=d(fx*,fy*)≤

Φ(d(x*,y*),d(x*,fx*),d(y*,fy*),d(x*,fy*),d(y*,fx*))≤

Φ(d(x*,y*),1,1,d(x*,y*),d(y*,x*)).

根据定理1和例1可得到如下分式压缩型不动点定理2.

定理2设(X,d)是完备的乘积度量空间,f:X→X是自映射.如果对任意的x,y∈X始终有

(10)

成立，则f有唯一不动点.

例3在R=(-∞,+∞)上定义函数d(x,y)=e|x -y|,∀x,y∈R, 则(R,d)是乘积度量空间[16].令X={1,2,5}, 则易知(X,d)是完备的乘积度量空间.定义f:X→X为f1=f2=1,f5=2，则:

当x=y=1时，有：

当x=y=2时，有：

当x=y=5时，有：

当x=1,y=2时，有：

当x=1,y=5时，有：

当x=2,y=5时,有：

由上述计算可知，对任意的x,y∈X, 式(10)都成立.由此根据定理2可知，f有唯一不动点1.

定理3设(X,d)是完备的乘积度量空间，定义f:X→X为自映射.如果存在k∈[0,1)且使得对任意的x,y∈X始终有

d(fx,fy)≤[max{d(x,y),d(x,fx),d(y,fy),d(x,fy),d(y,fx)}]k

(11)

成立，则f有唯一不动点.

证明定义d*(x,y)= lnd(x,y),∀x,y∈X, 则易证(X,d*)是完备的实度量空间.由式(11)可得,对任意的x,y∈X有：

d*(fx,fy)= lnd(fx,fy)≤k·ln[max{d(x,y),d(x,fx),d(y,fy),d(x,fy),d(y,fx)}]=

k·max{lnd(x,y),lnd(x,fx),lnd(y,fy),lnd(x,fy),lnd(y,fx)}=

k·max{d*(x,y),d*(x,fx),d*(y,fy),d*(x,fy),d*(y,fx)}.

(12)

注记1文献[13]中指出:如果完备的乘积度量空间(X,d)上的自映射满足如下乘积压缩条件：d(fx,fy)≤[d(x,y)]k，∀x,y∈X, 其中k∈[0,1)， 则f存在唯一不动点.该结果就是乘积度量空间上的Banach型不动点定理,等价于实度量空间(X,d)的Banach不动点定理(实度量空间上的Banach不动点定理中的压缩条件是d(fx,fy)≤kd(x,y),∀x,y∈X,k∈[0,1)).本文定理2中的压缩形式是实度量空间上的压缩形式,而文献[13]中的是方幂形式,并且其系数

是变系数，因此本文中的定理1和定理2很好地推广和改进了Banach不动定理及其相关定理.

定理4设(X,d)是乘积度量空间,f:X→X为自映射，且fX是完备的.如果存在Φ∈F且使得对任意的x,y∈X始终有

d(f2x,f2y)≤Φ(d(fx,fy),d(fx,f2x),d(fy,f2y),d(fx,f2y),d(fy,f2x))

(13)

成立，则f在X中存在1个不动点.

证明由fX⊆X可推出f(fX)⊆fX, 因此f*:=f|fX:fX→fX是自映射.于是由给定的条件可知，对任意的x*,y*∈fX, 存在x,y∈X使得x*=fx,y*=fy.由此再根据式(13)可得：

d(f*x*,f*y*)=d(f2x,f2y)≤

Φ(d(fx,fy),d(fx,f2x),d(fy,f2y),d(fx,f2y),d(fy,f2x))=

Φ(d(x*,y*),d(x*,f*x*),d(y*,f*y*),d(x*,f*y*),d(y*,f*x*)).

(14)

式(14)表明，f*在完备的乘积度量空间(fX,d)上满足定理1的所有条件.由此可知f*在fX上有唯一不动点，且f在X上至少存在一个不动点.