基于多目标优化的机组一次调频自抗扰控制

殳建军, 崔晓波, 于国强, 高爱民, 史毅越， 杨小龙， 张天海

(1.江苏方天电力技术有限公司，南京 211102； 2.南京工程学院 能源与动力工程学院， 南京 211167)

由于具有暂态性、随机性的风能、太阳能等新能源大规模并入电网，对电网频率的稳定性产生了不利影响[1]。为了抑制大电网的频率波动，具有较强灵活性燃气轮机的一次调频能力对于大电网频率的稳定具有重要的意义[2]。燃气轮机一次调频控制中大部分采用比例-积分(proportion-integral, PI)控制策略，这是由于PI控制器具有结构简单、性能可靠、易于实现、参数整定容易等优点[3]。然而由于PI控制器依赖“基于误差反馈消除误差”的反馈机制，使得其性能提升受到限制[4]。主要表现为：①闭环系统的动态品质对于PI控制器的增益比较敏感；②其反馈机制容易造成初始控制力过大，闭环系统产生“快速性”和“超调”之间的矛盾；③积分反馈的扰动抑制能力不足。

为了在保证闭环系统鲁棒性的前提下，提升控制品质和提高系统的抗干扰性能，韩京清[4]在通过对“模型论”和“控制论”的长期思考中提出了一种自抗扰控制(active disturbance rejection control, ADRC)的新型控制策略。ADRC具有不依赖精确数学模型、鲁棒性强、处理非线性能力强等优点，能够将任意系统转换成积分串联型对象，积分串联型对象之外的部分称之为总扰动，总扰动通过扩张状态观测器(extended state observer, ESO)进行实时估计和补偿。由于ADRC具有上述优点，在电力系统[5]、航天器系统[6]、机器人系统[7]、电动汽车系统[8]等领域得到成功应用。ADRC在能源系统也得到了广泛的应用[9]，文献[10]对ADRC在燃煤机组、燃气轮机、核电机组以及新型能源等电站中的广泛应用进行了总结和梳理。其中，ADRC在燃煤机组的协调控制系统、过热汽温系统、高加水位系统、炉膛负压系统以及二次风系统等进行了实际应用，取得了较原有控制策略更好的控制效果。

燃气轮机一次调频控制策略除了传统的PI控制策略[11]，还有结合神经网络等人工智能的控制策略[12]。但由于计算量大，实施难度较大，不具备工程应用价值[13]。研究具有抗干扰能力强、鲁棒性好和易于工程实现的燃气轮机一次调频控制策略是十分必要的。

ADRC能够很好地满足燃气轮机一次调频控制策略要求高控制精度、低模型依赖度等要求。为了提高燃气轮机一次调频中的控制效果，提出一种适用于燃气轮机一次调频的基于输出量直接反馈的ADRC结构。首先介绍重型燃气轮机一次调频模型，然后针对基于输出量直接反馈的ADRC，推导出所提ADRC的参数稳定域的计算方法，为ADRC参数优化提供优化范围；接着基于NSGA-Ⅲ多目标遗传算法，对ADRC参数进行优化，并通过水平图法得到具有满意鲁棒性和控制效果的ADRC参数；最后通过仿真验证所提方法在燃料量和转速控制方面的优势以及应对不确定性系统的能力。

1 重型燃气轮机一次调频模型

文献[14]介绍了一个以GE 公司生产的结和MARK V 控制系统的MS6001B重型燃气轮机模型，其Simulink/MATLAB结构如图1所示。经过分析可知其转速和燃料控制系统采用PI控制策略。该模型为简单循环单轴燃气轮机，以液体燃料为燃料，额定转速和额定功率分别为5 100 r/min和35.9 MW。此外燃气轮机的排烟温度为550 ℃，额定工况下大气温度为15 ℃，转速不等率取4%[11]。G1(s)和G2(s)为PI控制策略，该部分可以改用其他控制策略，如本文中提出的基于输出量直接反馈的ADRC或者其他控制策略。

从图1和表1可知，燃料控制系统的输出通过时滞和惯性环节后，结合f2(n,Gf)和积分环节可以得到转速，得到的转速作为转速控制系统的输出值，即转速控制系统和燃料控制系统组成一个类似串级控制系统，在设计控制器和参数优化时需要考虑该部分结构。

s、n、Gf和TR分别为微分算子、转速、燃料流量和排烟温度；G1(s)和G2(s)为反馈控制器；r、y、u分别表示闭环系统的设定值信号、系统的输出值和控制量；z1和z2为ESO的输出；b0和kp为控制器参数；Gp(s)为被控对象

表1 相关模型参数的物理含义和数值

2 基于输出量直接反馈的ADRC

标准一阶ADRC的结构如图2所示。任意实际系统Gp(s)可以将其转换成为一般的一阶对象，即

图2 标准一阶ADRC结构

(1)

(2)

(3)

f可以通过ESO进行估计，其表达式为

(4)

式(4)中：β1和β2为ESO的参数。当β1和β2整定合理时，z1、z2能够分别很好地跟踪y和f。

此时标准一阶ADRC的控制率为

(5)

由于z1、z2分别跟踪y和f，即z1≈y和z2≈f，结合式(3)和式(5)，可得

(6)

通过拉普拉斯变换可知此时闭环系统的响应为

(7)

即得到经过ADRC控制输出响应的预期动态方程，可知经过ADRC的控制能够将实际对象的输出动态接近预期动态响应。

由于燃气轮机机组的测量数据比较精准，测量噪声较小，考虑到ESO的输出z1用来估计可以直接测量得到y，本文中ADRC中控制率采用y替换z1，即

(8)

其结构如图3所示。由于ESO的估计滞后作用会使得z1在动态过程中会滞后于y，直接使用y能够解决该问题。

图3 基于输出量直接反馈的ADRC结构

此时，所提ADRC需要整定的参数有kp、β1、β2和b0。β1和β2与观测器带宽ωo之间存在如下关系[15]

(9)

为增加参数整定的自由度和灵活性，式(9)修改为

(10)

式(10)中：ξ为调整系数，一般取值在0.1～10。

由于本文中采用基于多目标遗传算法对所提ADRC的参数进行优化，需要在ADRC的稳定域内生成初始化种群， 接下来对所提ADRC的稳定域进行推导和分析。

基于文献[16]中方法，可以得到如图4所示的等价结构，其中Gc(s)和Gf(s)分别为等价结构的反馈控制器和前馈控制器，其表达式分别为

图4 本文ADRC的等价结构

(11)

(12)

被控对象Gp(s)的频域响应可以表示为

Gp(jω)=rp(ω)eiϑp(ω)=ap(ω)+jbp(ω)

(13)

式(13)中：ap(ω)和bp(ω)分别是被控对象的实部和虚部；rp(ω)和ϑp(ω)分别是被控对象的幅值和相角。类似地，可以得到反馈控制器的频域响应为

Gc(jω)=rc(ω)eiϑc(ω)=ac(ω)+jbc(ω)

(14)

式(14)中：ac(ω)和bc(ω)分别是Gp(s)反馈控制器的实部和虚部；rc(ω)和ϑc(ω)分别是被控对象的幅值和相角。此时，闭环系统的特征方程为

Ecl(s)=1+Gc(s)Gp(s)=0

(15)

接下来采用D-分割法求解一阶ADRC的稳定域。D-分割法原理中控制器的稳定域边界由ω∈(0,-∞)∪(0,+∞)时的非奇异边界∂Dω以及ω=0、ω=±∞时的奇异边界∂D0和∂D∞组成[17]。

(1)ω=0时的奇异值边界∂D0为

∂D0:Ecl(j0)=kpβ2=0

(16)

(2)ω=±∞时的奇异值边界∂D∞为

∂D∞:G(±j∞)=b0bp(ω)|ω=±∞=0

(17)

由于b0是被控对象的高频增益的估计值，有b0≠0。故此部分没有ADRC参数，可以忽略。

(3)ω∈(0,-∞)∪(0,+∞)时的非奇异值边界∂Dω为

∂Dω:1+[ac(ω)+jbc(ω)][ap(ω)+jbp(ω)]=0

(18)

令式(18)的实部和虚部分别为0，可以得到ADRC的非奇异值边界∂Dω为

(19)

结合式(10)，将式(11)代入式(19)，可得

(20)

综合式(1)～式(3)，ADRC是稳定域，其决定条件为

(21)

通过求解式(21)得到ADRC稳定域边界，其组成的面积为ADRC的稳定域。以式(22)作为被控对象为例，有

(22)

当ξ和b0分别固定时，通过求解式(21)，可以得到图5所示的结果。从图5(a)可知当ξ=1时，随着b0的增加时ADRC的稳定域也逐渐增加。相反地，从图5(b)可知当b0=1时，随着ξ的减小时ADRC的稳定域也逐渐增加。因此在优化ADRC参数时，可以合理选择ξ和b0的范围，对于优化ADRC的目标参数十分有必要。本文中推荐ξ∈[0.1～10]和b0∈[0.5～10]b。

图5 分别固定ξ、b0时所得ADRC的稳定域

3 基于NSGA-Ⅲ多目标遗传算法的ADRC参数整定

多目标遗传算法NSGA-III算法是基于参考点的非支配排序方法，通过采用中参考点的方法实现非支配的种群成员且能够保证种群与所提供的参考点距离很近[18]。其整定流程如图6所示，首先通过式(21)计算ADRC的稳定域，在稳定域内随机生成初始种群，然后通过定义的多目标函数，对种群中个体进行进化，最后达到满足终止条件(目标函数均满足一定条件或者种群进化代数达到某一值)。根据图6所示流程，可以得到具体的基于NSGA-Ⅲ多目标遗传算法的ADRC参数整定流程如下。

图6 基于NSGA-Ⅲ多目标遗传算法的ADRC参数整定流程

(1)基于已知的被控对象的模型信息，根据式(21)计算ADRC的稳定域，用于生成NSGA-Ⅲ的初始种群。

(2)采用NSGA-Ⅲ规则对种群内个体进行优化，通过非支配分层和从最后一个非支配层级中挑选个体进入子代，迭代一定代数后得到Pareto最优解集。

(3)采用水平图法得到ADRC的参数。

为了说明基于NSGA-Ⅲ多目标遗传算法的ADRC参数整定流程，针对式(22)的被控对象，定义多目标函数为

(23)

式(23)中：误差绝对值积分(integrated absolute error, IAE)为控制性能指标，下标“sp”和“id”分别表示跟踪性能指标和抗干扰性能。通过对式(22)中被控对象的IAEsp(J1)和IAEid(J2)，可以得到Pareto最优解集如图7所示，从图7可知，跟踪性能与抗干扰性能是相互矛盾的，即在保证较强的抗干扰性能时，闭环系统的跟踪性能会有下降，反之亦然。

图7 基于NSGA-Ⅲ多目标遗传算法得到的Pareto最优解集

图8 基于的Pareto解集

图9 基于的参数集

基于得到的参数，可以得闭环系统的阶跃响应以及在50 s时添加输入扰动的结果，如图10所示。其中“最优抗干扰”和“最优跟踪”两种对比方法是分别将IAEid和IAEsp作为唯一优化目标得到的ADRC参数，“最优抗干扰”的参数为kp=4.109、b0=0.950 3、ωo=2.584和ξ=0.328 7；“最优跟踪”的参数为kp=4.929、b0=0.765、ωo=0.641 6和ξ=3.520 1。从图10可知，本文所提方法能够很好地均衡跟踪与抗干扰性能，对比“最优抗干扰”和“最优跟踪”法能够分别实现抗干扰与跟踪性能的优化。此外“最优抗干扰”法的控制量会有较大的变化，会对执行器产生较大的磨损，不利用执行器的长期安全运行。

图10 闭环系统输出和控制量

图11中指标值越小表征闭环系统的性能越好，越集中表征控制器的鲁棒性越强。从图11中可知，本文所提方法得到的上述指标能够比较好地集中在一定范围内，这意味着本文所提方法的鲁棒性较强。综合上述分析可以，本文所提的基于NSGA-Ⅲ多目标遗传算法的ADRC参数整定在保证鲁棒性的前提下能够较好地平衡跟踪与抗干扰性能，展现了很强的工业应用潜力。

图11 系统存在不确定性时的Monte Carlo结果

4 仿真验证

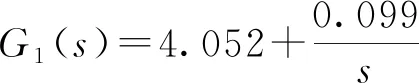
在稳定工况下负荷稳定在标称工况，在100 s时机组接受到一次调频上升信号，转速要求在100 s时上升0.002 5并稳定，在600 s时再次上升0.002 5并稳定，1 100 s时转速要求下降0.005 0并稳定，可以得到图12和图13所示结果。需要说明的是各个变量采用单位制形式，即在标称工况下时值为1，并在此基础上进行变化。变化过程中燃料和转速的变化情况如图12所示，可知本文提出的基于NSGA-Ⅲ多目标遗传算法的ADRC能够有效在减少燃料量超调的同时具有更快的跟踪速度，转速尽管具有更大的超调但是能够快速达到稳态值，具有更强的一次调频能力。图13为燃料量和转速对应的控制量，可知本文ADRC为了实现更快的跟踪效果具有较强的控制量动作。

图12 一次调频中Gf和n的输出

图13 一次调频中燃料量阀门开度和单位速度

由于燃气轮机中动态参数随着机组老化以及建模简化等原因会造成模型存在一定的不确定性，为了比较控制器的鲁棒性，Monte Carlo实验法也在这里进行应用。首先将表1中燃气轮机的动态参数分别在初始值附件的±20%附近摄动，然后保持控制器参数不变，然后进行图12所示的仿真200次，记录每次仿真中的J1和J2，可以得到图14所示的结果。从图14中可知，本文所提方法得到的指标能够比较好地集中在一定范围内，这意味着本文所提方法具有较基于NSGA-Ⅲ多目标遗传算法的PI方法具有更强的鲁棒性。综上所述，本文提出的基于NSGA-Ⅲ多目标遗传算法的ADRC设计方法具有很强的实用性，能够有效燃气轮机的一次调频能力，展示了很强的工业应用潜力。

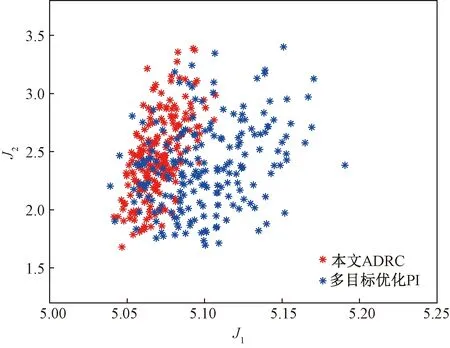
图14 燃气轮机存在不确定性时的Monte Carlo结果

5 总结与展望

本研究致力于提高燃气轮机的一次调频能力，提出了基于多目标遗传算法的自抗扰控制策略，主要工作如下。

(1)首先提出了一种基于输出量直接反馈的自抗扰控制结构，并推导出其参数稳定域的计算公式。

(2)在介绍NSGA-Ⅲ多目标遗传算法的基础上，提出了基于多个控制性能指标的多目标参数优化流程，并将该方法应用于燃气轮机机组的一次调频控制策略设计中。

(3)仿真结果表明，提出的基于多目标遗传算法的自抗扰控制策略在保证鲁棒性的前提下能够提高燃气轮机机组一次调频的性能，显示了很好的应用前景。