W型永磁电机转矩脉动分析与抑制方法

童拉念， 高霆， 高艳红， 许明俊， 颜世龙， 孙瑞丰， 尹红彬

(1.山东唐骏欧铃汽车制造有限公司， 淄博 255000； 2.山东理工大学交通与车辆工程学院， 淄博 255000；3.山东农业大学林学院， 泰安 271000)

永磁同步电机因具有高功率密度、高效率等优点被广泛应用于各类工程领域。转矩脉动将会使永磁同步电机产生振动与噪声，从而严重影响电机的平稳运行。但因永磁同步电机的固有结构，不可避免地会产生转矩脉动[1-2]，分析转矩脉动产生机理并研究其抑制方法对于永磁同步电机的设计与优化具有重要意义。

转矩脉动主要由齿槽转矩、永磁转矩脉动与磁阻转矩脉动组成，为了抑制转矩脉动，中外学者多从电机控制以及电机本体设计两个方面进行研究。崔兆蕾等[3]提出一种注入补偿电压的方法抑制谐波电压，王琴剑等[4]提出一种基于模糊控制的新型控制方法以削弱转矩脉动，从电机控制的角度减小转矩脉动效果显著，但控制方法过于复杂，不易于广泛应用。因此大部分学者从电机本体的角度对永磁电机转矩脉动进行研究，宋守许等[5]提出一种开设偏心槽的转子再设计方法以减小转矩脉动，崔康宁等[6]提出一种大小不对称磁极的方法抑制电机振动与噪声，刘爱民等[7]提出添加辅助线圈的方法抑制转矩脉动，以上方法虽然削弱了转矩脉动，但受制于技术成熟度、电机其他电磁性能下降等因素，无法大范围推广。目前中外对转子斜极与分段斜极的方法[8-11]研究较为全面与深入，但该方法对加工工艺要求较高，且斜极所产生的切向力对轴承的损害较大。为避免上述方法带来的各种问题，现从电机本体设计出发，采用一种具有更好聚磁效果的W型永磁同步电机，以抵消电机转子再设计时所产生的电磁性能下降的问题，并从中找到平衡点。

W型永磁同步电机具有较强的聚磁效果与防漏磁能力，但该类型电机转矩脉动相对较大，深入分析其转矩脉动影响因素，并采取有效措施削弱转矩脉动，将会得到一款转矩密度更大、性能更加卓越的永磁同步电机。目前中外对转矩脉动的研究计算多使用傅里叶展开[12]、子域法[13-14]等计算方法，但傅里叶展开所得到的转矩表达式精度较低，且不易分析结构较为复杂的磁场分布；而子域法虽然精度高，但计算难度较大，不利于快速定位到具体参数。因此，以一台7.5 kW的W型永磁同步电机为例，利用精度较高、计算方便的等效磁路法与绕组函数理论得出电机转矩表达式，并基于此对W型永磁体的位置参数进行进一步优化，同时对该类型电机转矩脉动的抑制方法进行研究。

1 电机结构简述

选用的样机为一台功率为7.5 kW的三相永磁同步电机，极槽配比为6极36槽，定子铁心与转子铁心均由硅钢片压叠而成，电枢绕组采用单层整数槽集中绕组串联而成。转子每个磁极由4块永磁体组成，永磁体呈W型分布，永磁材料为钕铁硼(NdFe35),转子结构如图1所示。

图1 W型永磁同步电机转子结构

由图1可以看出，W型永磁同步电机磁极位置关系较为复杂，应着重分析永磁体位置对转矩脉动的影响规律，电机初始参数如表1所示。

表1 电机初始参数

2 转矩脉动分析

2.1 定子磁动势

假设不考虑定子磁轭饱和，且其他情况为理想条件，定子导体可由沿气隙表面外侧的电流片建模[15-16]，则对A相绕组磁动势傅里叶分解展开可得

(1)

式(1)中：Na(θ)为A相绕组通电后在气隙中产生的磁动势分布函数；θ为沿气隙分布的机械角度；h为谐波次数；nh为定子绕组h次谐波幅值。若电枢绕组的三相电流为

Ia,b,c=Imcos[ωrt-(k-1)π/3-γd]

(2)

此时电机定子部分产生的磁动势Fs可以表示[17-18]为

i=1,9,11,…

(3)

式(3)中：Im为三相电流幅值；ωrt为转子瞬时位置；k取1、2、3分别对应三相绕组；γd为三相电流相对于d轴的电流角；Ksh为h阶定子磁动势系数，取值范围为

(4)

2.2 转子磁动势

在W型永磁同步电机中，转子磁极两侧的大永磁体与中部的小永磁体所产生的磁路并联，对其进行初步有限元仿真可以得到其磁通分布情况，如图2所示。

由图2可知，侧部永磁体与中部永磁体分别产生两条主磁通路径，每个永磁体两端均有不同程度的漏磁，其中侧部永磁体靠近定子一端漏磁最为严重。由于两磁路并联，因此分别对两条磁通路径解析建模。

图2 电机磁路仿真图

侧部永磁体所产生的等效磁路如图3所示。

Fr1为侧部永磁体产生的等效磁动势，Fs1为侧部永磁体在定子产生的等效反电势，Rm1为侧部永磁体等效磁阻，Rrm1为侧部永磁体外端磁桥的漏磁磁阻，Rδ1、Rδ2为侧部永磁体两端磁障等效磁阻，Rs1为定子轭磁阻，Rr1为转子轭磁阻，Rg1为气隙磁阻，Φr1为侧部永磁体所产生的磁通量，Φrm1为磁桥漏磁磁通，Φδ1、Φδ2为磁障漏磁磁通，Φg1为经过气隙的主磁通

因为该方法假设磁轭中磁密未饱和，所以定子轭磁阻Rs1与转子轭磁阻Rr1远小于气隙磁阻Rg1，可以忽略不计。且由于侧部永磁体对称放置，等效磁路图可简化为如图4所示。

图4 侧部永磁体等效磁路简化图

由克希霍夫定律可得磁路关系，即

(5)

式(5)中参数结合图1，由几何关系、磁路计算相关公式可得

(6)

式(6)中：μ0为真空磁导率；μr为永磁体磁导率；xm为侧部永磁体长度；L为转子轴向长度；hm为侧部永磁体充磁方向厚度；gair为气隙长度；Ag1为侧部永磁体产生磁通量在转子内的横截面积；Hc为永磁体矫顽力；Br1为永磁体剩磁；am为侧部永磁体距转子极面距离；α0、β2分别为中部永磁体、侧部永磁体所占机械角度；rg为气隙半径；Ke为磁通系数；f为电源频率；N1为定子绕组每槽匝数。

式(5)中Rδ1、Rδ2数值相对较大，则通过的漏磁通量Φδ1、Φδ2较小，求解时忽略不计。结合式(5)、式(6)可得侧部永磁体产生的气隙磁通为

(7)

其产生的气隙磁密为

(8)

同理对中部永磁体进行磁路分析，其简化等效磁路图如图5所示。

Fr2为中部永磁体产生的等效磁动势，Fs2为中部永磁体在定子产生的等效反电势，Rm2为中部永磁体等效磁阻，Rδ3、Rδ4为中部永磁体两端磁障等效磁阻，Rg2为气隙磁阻，Φr2为中部永磁体所产生的磁通量，Φδ3、Φδ4为磁障漏磁磁通，Φg2为经过气隙的主磁通

由图5可知，中部永磁体两端的漏磁通较少，可见中部永磁体具有良好的减少漏磁、聚磁的效果，可得其磁路关系为

(9)

(10)

式中：xn为中部永磁体长度；hn为中部永磁体充磁方向厚度；Ag2为中部永磁体产生磁通量在转子内的横截面积；Br2为永磁体剩磁；b为中部永磁体间隔距离。同样忽略永磁体两端较小的漏磁通，结合式(9)、式(10)可得中部永磁体产生的气隙磁通为

(11)

其产生的气隙磁密为

(12)

永磁体在气隙内层产生的h阶磁动势可表示为

(13)

则

(14)

转子磁动势可表示为

h=1,9,11,…

(15)

2.3 电机转矩脉动

在气隙表面，根据以上公式，由洛伦兹力定律可推导出电机瞬时转矩[19]表达式为

(16)

从函数的周期性考虑，有

所以，电机瞬时转矩可简化为

(17)

对Fs、Fr傅里叶展开可得

h=10m±1，m=1，2，3，…

(18)

最后可以得到电机平均转矩T0与转矩脉动Th表达式

(19)

(20)

由以上推导可以得出，W型永磁同步电机的转矩脉动与W型永磁体的放置位置及角度有较大关系，合理的放置永磁体有利于降低转矩脉动。

3 永磁体位置关系解析与优化

3.1 永磁体位置几何关系解析

组成W型的四段永磁体的位置参数与其所占机械角度α0、β2息息相关，定义中部永磁体夹角为βn、侧部永磁体夹角为βm，如图6所示。

图6 W型永磁体位置参数

由图6可得到永磁体位置参数与所占机械角度的几何关系为

(21)

(22)

式(22)中：R为转子外径。可知，在永磁体体积不变的前提下，影响发电机的重要参数α0与β2可由永磁体夹角以及永磁体距转子极面距离表示。因此本文着重研究W型永磁同步电机中侧部永磁体夹角βm、中部永磁体夹角βn、中部永磁体距转子表面距离an、侧部永磁体距转子表面距离am对转矩脉动的影响规律，同时为验证前文分析的正确性，建立有限元模型进行仿真验证。

3.2 确定永磁体位置

四个永磁体位置关系参数并非相互独立，而是相互影响的，为使变量尽量减少，首先确定中部永磁体位置。假设侧部永磁体位置保持不变，改变中部永磁体距转子极面距离an，使其在5～12 mm变化，可得电机转矩变化情况如图7所示。

由图7可知，an的变化对输出转矩影响较小，为计算方便，取an=11 mm，此时电机输出的平均转矩较大且转矩波动较小。确定an后，保持am=2 mm不变，研究W型永磁体之间夹角对转矩的影响规律。

图7 an改变时平均转矩与转矩脉动的变化情况

使侧部永磁体夹角βm不变，改变中部永磁体夹角βn，使其在30°～100°改变，变化步长为10°，可得此时输出转矩变化情况如图8、图9所示。

图8 βn改变时输出转矩的变化情况

图9 βn改变时平均转矩与转矩脉动的变化情况

由图8、图9可知，中部永磁体夹角βn的改变对电机对于转矩脉动影响较大，当βn由30°～50°变化时，转矩脉动由29%降低至19%；当βn大于50°时，转矩脉动持续升高至接近40%。因此选取合适的βn值尤为重要。

另单独考虑βm改变对电机输出转矩的影响，保持βn不变，使βm在45°～135°变化，变化步长为10°，可得电机转矩变化情况如图10、图11所示。

图10 βm改变时输出转矩的变化情况

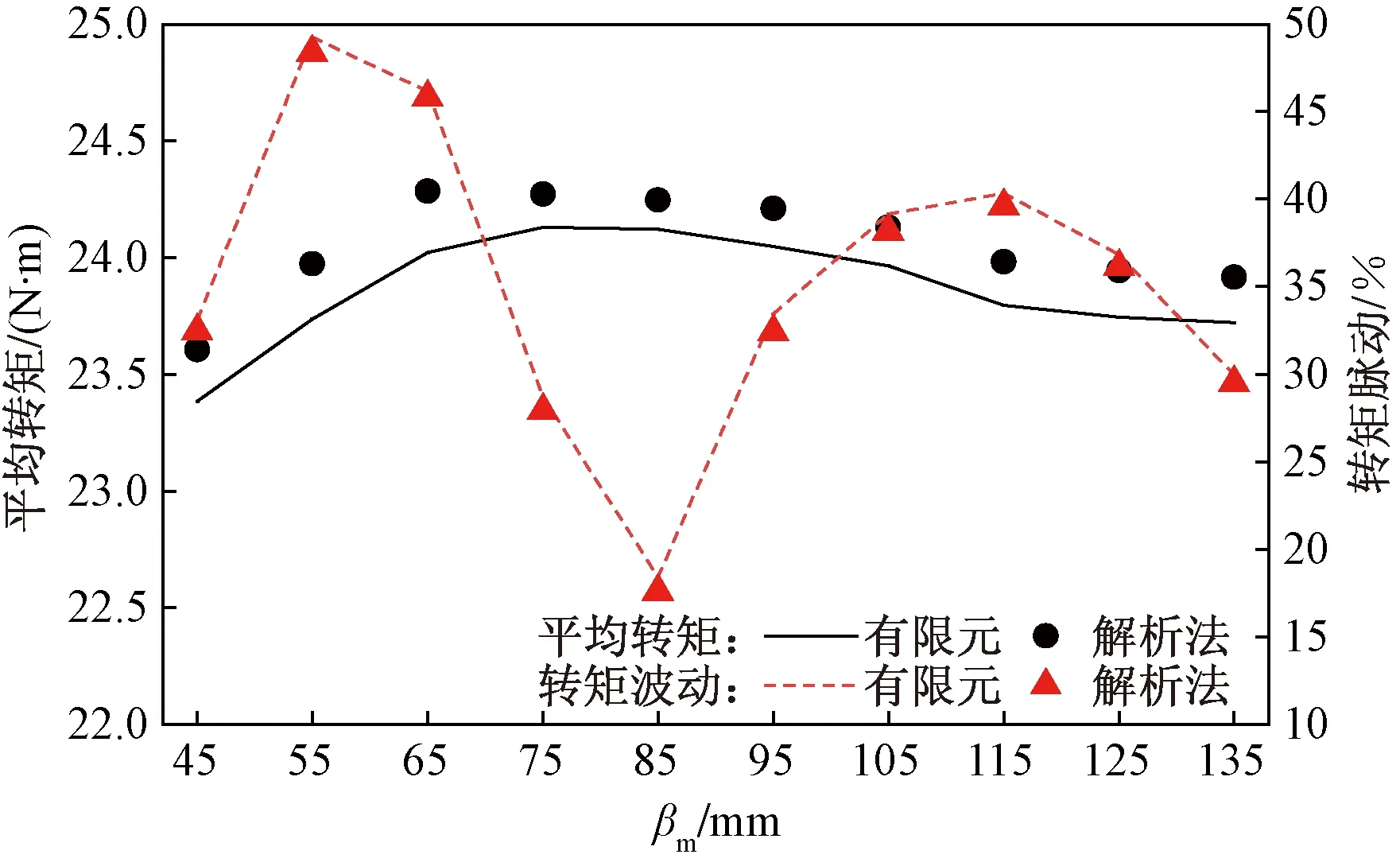
图11 βm改变时平均转矩与转矩脉动的变化情况

由图10、图11可知，与中部永磁体夹角类似，侧部永磁体夹角βm对转矩脉动的影响同样较大，且在45°～135°存在最优βm使得电机平均转矩基本不变的同时，转矩脉动较小。因此应对两夹角进行联合研究，取βn于30°～100°变化，βm于45°～135°变化，变化步长均为10°，可得此时电机转矩变化情况如图12、图13所示。

图12 βn、βm同时变化时平均转矩的变化情况

图13 βn、βm同时变化时转矩脉动的变化情况

由图12、图13可知，永磁体夹角在一定范围内变化时，对电机的平均转矩影响较小，但转矩脉动将产生较大变化。当取βm=85°、βn=80°时，电机输出性能较好，平均转矩为24.12 N·m，转矩脉动为18.4%，此时电机的输出转矩与齿槽转矩如图14所示。

图14 最佳永磁体位置时输出转矩与齿槽转矩

由图14可知，调整永磁体位置后，电机的转矩脉动依旧较大，其中齿槽转矩峰值约为400 mN·m，电机仍需进一步优化以抑制转矩脉动。

4 转矩脉动抑制方法

目前电机本体研究中，抑制转矩脉动的主要方法为转子磁极偏移、转子斜极与分段斜极等。但对于W型永磁同步电机，磁极偏移所产生的变量过多，不易确定最佳偏移方式；由于每极有四段永磁体，采用转子斜极与分段斜极等方式时转子加工过于复杂。转矩脉动主要由齿槽转矩与纹波转矩组成，气隙磁密的谐波含量对两者有重要影响[20]，因此削弱气隙磁密谐波含量能够减小电机的转矩脉动，而转子极面偏心则是提高气隙磁密正弦性的有效手段[21]。转子极面偏心方式如图15所示。

图15 转子极面偏心

当电机其余参数皆不变时，其中转子每极对应气隙磁密的分布函数B(λ,ε)可表示为

(21)

式(21)中：Br为永磁体剩磁；lm(λ)为转子外径与内径之差；δ0(λ,ε)为转子未偏心时有效气隙长度；λ为与磁极中心线相差角度；ε为定子与转子之间相对位置角。

结合图15可得转子极面偏心时每极对应气隙磁密表达式

(22)

式(22)中：s为偏心距。由式(22)可知，转子偏心时偏心距对气隙磁密影响较大，应选取合适的偏心距以最大限度地削弱气隙磁密谐波含量。

利用有限元软件分析转子偏心对电机性能的影响规律，使偏心距s=10 mm，可得气隙磁密变化情况如图16、图17所示。

由图16、图17可知，转子极面偏心后，气隙磁密波形正弦性有所提高，基波幅值虽然略微下降，但5、7次谐波幅值大幅下降，其余阶次谐波幅值也均有下降。谐波含量的减少意味着电机的转矩脉动与齿槽转矩将得到抑制，变化情况如图18所示。

图16 偏心前后气隙磁密变化情况

图17 偏心前后气隙磁密谐波峰值变化情况

由图18可知，偏心后电机的转矩脉动明显下降，齿槽转矩峰值由412 mN·m降为78 mN·m，齿槽转矩的大幅下降有利于电机转矩脉动的抑制。显然转子极面偏心能够有效减小转矩脉动，因此对偏心距数值进一步优选，使偏心距s于10～15 mm改变，变化步长为0.5 mm，可以得到电机输出转矩的变化情况如图19、图20所示。

图18 偏心前后输出转矩与齿槽转矩变化情况

图19 偏心距改变时输出转矩变化情况

图20 偏心距改变时平均转矩与转矩脉动变化情况

由图19、图20可知，随着偏心距s的增大，电机的平均转矩基本呈线性增长；当s在10～14 mm变化时，电机转矩脉动随着偏心距的增大而减小，但当s>14 mm时，转矩脉动呈增长趋势。因此对于该电机而言，偏心距取14 mm为宜，此时电机的平均转矩为25.5 N·m，转矩脉动仅为6.4%，电机输出性能有了较大提升。

选取合适的偏心距后，电机的平均转矩略微提高，由未偏心时的24.12 N·m提升到25.5 N·m；但转矩脉动大幅下降，由18.4%降低为6.4%。显然转子极面偏心能够有效抑制转矩脉动，且能够保证电机平均输出转矩满足设计要求。

5 总结

对W型永磁同步电机的转矩脉动进行了深入研究，通过等效磁路法得到电机的有效磁通，进而得到转矩脉动解析式，并基于解析式对永磁体位置参数进行优化。为解决选择合适永磁体位置参数后电机转矩脉动依旧过大的问题，采用了转子极面偏心的方法，转子极面偏心能够有效降低电机气隙磁密的谐波含量，从而降低转矩脉动。

研究表明，就该电机而言，W型永磁体的最优布置方案为：中部永磁体夹角取80°，侧部永磁体夹角取85°，且四段永磁体底部齐平。该方案下电机的转矩脉动为18.4%，对转子极面偏心且选取合适的偏心距后，电机的转矩脉动降为6.4%，降低了12%。转矩脉动的降低有利于减小电机的振动与噪声，电机的整体性能得到显著提升。