磁阻型电磁发射的建模分析与仿真研究

张景卓，姚陆锋，杨绍华

(海军工程大学 物理教研室，湖北 武汉 430033)

电磁发射技术是一种利用电磁力做功把电磁能转化成机械能并把弹体发射出去的技术.电磁发射在科学研究、工业、航天及军事等领域有着不可估量的应用潜力，已成为一个研究热点.电磁发射一般可分为轨道型、线圈型和重接型.根据加速机理的不同，线圈型电磁发射又分为感应型和磁阻型两种类型[1，2].

磁阻型电磁发射本质上是利用线圈磁场与磁化后的铁磁性弹体之间的作用力来加速弹体的，具有结构简单、可控性好、可靠性高等优点，在军事上有着重要应用前景[3].美国Texas大学Austin分校机电研究中心开展了磁阻型电磁发射的理论和控制策略研究[4]；波兰的Tomczuk等[5]主要对磁阻型电磁发射的磁场进行了分析；马来西亚的Rezal等[6]进行了单级磁阻型电磁发射的仿真与实验研究；国防科大的刘元恒等[7]进行了磁阻型电磁发射的机理和试验研究.G.William Slade 分别运用电磁系统的拉格朗日函数法[8]和有限元法[9]对磁阻型电磁发射进行了建模研究；Zhao Keyi等[10]利用有限元法结合虚功原理对磁阻型电磁发射进行建模研究.但是这些分析与建模研究都需要电动力学、分析力学等专业理论知识，不便于将研究热点引入大学物理课堂.本文在大学物理理论知识的基础上，利用磁矩模型对磁阻型电磁发射进行建模分析和仿真研究，使建模与分析大为简化，易于理解，其结果可为单级及多级磁阻型电磁发射的分析及参数优化提供参考.

1 发射机理

单级磁阻型电磁发射原理如图1所示，发射线圈为多层密绕直螺线管，弹体为柱状铁磁性材料.当开关拨向a点时，电源向储能电容器充电；当开关拨向b点时，储能电容器向发射线圈迅速放电，从而激发瞬变磁场，对铁磁性弹体进行磁化.磁化后的弹体由于受到发射线圈磁场的作用而被加速，从而被发射出去，这一作用相当于磁场对磁矩的作用.

2 建模分析

2.1 发射模型

磁阻型电磁发射系统实际上是一个复杂的机电复合系统，为了分析发射过程的物理本质，本文对系统作合理简化，将磁化的铁磁质弹体等效为具有磁矩的磁介质.基本假设如下：1) 多层密绕直螺线管通电后所产生的磁场具有轴对称性，除端部外，简化为只有均匀分布的轴向磁场，并假设端部的磁场轴向小区域内均匀;2) 由于弹体在极短的时间内就完成了发射，为简化弹体的磁化过程，将弹体整个磁化过程的磁化率假设为一常数，它实际上是弹体在变化磁场中的等效磁化率，可以通过实验来确定.从而假设铁磁质弹体在均匀磁场作用下小区域瞬间均匀磁化；3) 磁化的铁磁质弹体等效为具有磁矩的磁介质，小区域磁矩为常数；4) 为了简化发射线圈与弹体的相互作用力的分析，磁化的弹体不影响原磁场；5) 由于本文涉及的发射线圈的电流及其变化率均较小，可以忽略涡流效应.

2.2 电路模型

由于单级磁阻型电磁发射系统的发射线圈具有一定的电阻，因此发射电路实际为串联RLC电路.在本文的实验条件下，分有无弹体2种情况，测得发射线圈两端的电压UL随时间t变化的曲线如图2所示，通过对比可知发射时磁化的弹体对发射电路的影响较小，因此可以将发射电路等效为串联RLC暂态电路，如图3所示，其中C为储能电容器的电容，L为发射线圈的电感，R为发射线圈的电阻，E为储能电容器的充电电源.

图2 单级磁阻型电磁发射的发射线圈电压UL随时间t变化曲线(L=1.9 mH，R=1.07 Ω，C=6600 uf，U=36 V，弹体Φ=8 mm，l=40 mm，m=14.9 g)

图3 单级磁阻型电磁发射等效电路

串联RLC暂态电路放电时，当发射电压E、电感L和电阻R一定时，电感L中的电流i(t)随时间t的变化有过阻尼、临界阻尼和阻尼振荡3种规律[11]，如所示图4.电路处于临界阻尼状态时，电流变化最快，弹体经过发射线圈后半部时阻碍就小，电流最大值为

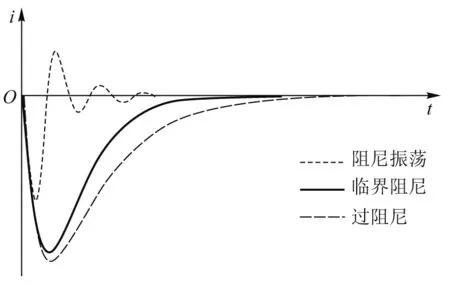
图4 发射电路放电过程中i随时间t的变化曲线

(1)

为了给发射线圈通入瞬时大电流，发射电路必须处在临界阻尼的状态，要求

(2)

由式(1)可知，提高发射电压E、减小发射线圈电阻R可以提高发射电流.而发射线圈电感L与电阻R是相互联系的，由发射线圈的结构所决定，发射线圈一旦确定，电感L与电阻R就确定了.由式(2)计算出电容值C，再求解串联RLC暂态电路方程，便可得到发射线圈中任意时刻的电流i(t).

当发射线圈中通入电流i(t)时产生的磁场为

(3)

式(3)中z为发射线圈中某场点的位置，r0、ri和L分别为发射线圈的内径、外径和长度，nz和nr分别为发射线圈的轴向和径向匝密度.

2.3 弹体动力学分析

为了分析弹体在发射线圈磁场中的受力，建立如图5所示的坐标系，其中OZ轴以发射线圈中点为原点，发射线圈轴线为坐标轴，O′ξ轴建立在弹体上，以弹体的中点为原点，弹体的轴线与OZ轴重合.发射线圈及弹体的尺寸如图5所示.

图5 弹体在通电螺线管线圈磁场中的受力分析图

由于具有磁矩m的磁介质在磁场强度为B的磁场中受力[12]为

F=∇(m·B)

(4)

设某时刻弹体中心点O′的坐标为z，根据上式及所建的模型可导出弹体在磁场中所受的轴向磁场力Fz为

(5)

式中μ0为真空磁导率，χm为弹体材料的磁化率，r和l分别为弹体的长度，Bz和∂Bz/∂Z分别为发射线圈轴向磁场强度、轴向磁场强度的梯度.铁磁质弹体在发射线圈的轴向磁场力Fz的作用下加速并被发射出去.由式(5)可知：弹体所受轴向磁场力的大小与发射线圈轴向磁场强度分布、轴向磁场梯度分布、弹体的几何尺寸、弹体中心的初始位置以及弹体材料的磁化等因素有关.根据式(3)可知发射线圈轴向磁场强度分布和轴向磁场梯度分布，除了与所通的电流及场点的位置有关外，还与发射线圈本身的结构有关.因此为了提高弹体的发射效果，必须优化发射线圈的结构.通过分析可知，发射线圈后半部分的磁场梯度为负值，弹体通过发射线圈中点后即受到一阻碍作用，磁场强度和磁场梯度乘积越小阻碍作用就越小.

设发射电路开始发射时的时刻为t=0，只要知道了弹体在t时刻的位置z，由式(5)便可得出弹体在t时刻所受磁场力的大小.而弹体受到的发射线圈磁场力又会影响弹体运动状态(z(t)、v(t))，因此弹体在发射线圈磁场中的受力与运动状态是相互联系的.设弹体的质量为m，发射时弹体中心处于z0处，初速度为v0=0，忽略弹体加速时空气阻力、发射管内壁的摩擦阻力，则根据牛顿力学可得弹体的轴向加速度az、轴向运动速度vz及轴向位移z为

(6)

(7)

(8)

由式(5)、(7)和(8)可知弹体的发射速度与弹体中心的初始位置z0也有关系.

3 仿真分析

根据式(5)—式(8)结合串联RLC暂态电路方程，利用MATLAB编程来模拟单级磁阻型电磁发射过程，如图6、图7、图8和图9.其中发射线圈内径Φ15 mm、外径Ф28 mm，轴向、径向匝密度为768匝/m，电感为1.9 mL，电阻为1.07 Ω；根据式(2)，与发射线圈匹配的储能电容C=6639 uF，由2200 uF/450 V的电解电容利用串并联组成；弹体为Φ8 mm、长分别为20 mm、30 mm、40 mm和50 mm的柱状软铁，质量分别为7.3 g、11.1 g、15 g和18.8 g；发射管为内径φ=9 mm、外径φ=15 mm的有机玻璃管.

1. 储能电容器；2. 开关；3. 铁磁性弹体；4. 发射线圈；5. 电源；6. 发射管图1 单级磁阻型电磁发射原理

图6中的弹体为长为40 mm、质量为15 g，弹体前部刚刚处于发射线圈入口处，储能电容器与发射线圈匹配.由图6可知，弹体发射时的典型发射过程为：在发射线圈前半部分先经历一个加速过程，在发射线圈后半部分再经过一个减速过程，到达管口时速度稳定.这与文献[8]用拉格朗日函数法建模分析、文献[10]用有限元法结合虚功原理建模分析及文献[13]、[14]利用Ansoft软件进行有限元的模拟等结果非常类似，说明本文的建模方法具有一定的合理性.由图6可知，减速过程随发射电压变化而变化，发射电压越大，减速过程越明显，发射电压越小，减速过程越不明显，甚至没有减速过程.弹体的发射速度与发射电压的关系为非线性关系.适当提高发射电压可以提高发射速率，但是发射电压较高时，减速过程就越明显，速度的提高就越困难.文献[15]实验结果证实了适当提高发射电压可以提高发射速率.

图6 弹体在不同发射电压时的速度v和时间t关系曲线

图7中的弹体为长为40 mm、质量为15 g，发射电压U=100 V，储能电容器与发射线圈匹配c表示弹体前部与发射线圈入口的距离，c> 0表示弹体前部与发射线圈入口有一定的间距，c< 0表示弹体前部插入发射线圈内部一定的深度.由图7可知弹体发射存在一个最佳的初始位置，略为改变初始位置有可能使弹体的发射速度发生明显的改变.文献[16]实验结果证实了弹体发射存在一个最佳的初始位置.

图7 在不同初始位置时的弹体速度v和时间t关系曲线

图8中的弹体为长为40 mm、质量为15 g，发射电压U=100 V，弹体前部刚刚处于发射线圈入口处.由图8可知，发射电路处于临界状态或较小的过阻尼时，弹体的发射速度较大.发射电路处于欠阻尼或较大的过阻尼状态都不利于弹体的发射.另外，发射电路处于欠阻尼状态时，电路存在振荡现象，对储能电容器产生反向充电，不利于保护由电解电容组成的储能电容器组.文献[15]实验结果证实了储能电容器参数对弹体发射速率有影响.

图8 不同发射电路状态时的弹体速度v和时间t关系曲线

图9中弹体前部刚刚处于发射线圈入口处，发射电压U=100 V，储能电容器与发射线圈匹配，l为弹体的长度.由图9可知，在发射线圈、发射电压、储能电容器及弹体初始位置一定的条件下，存在一个最优的弹体长度，这与发射线圈的磁场及磁场梯度分布有关.

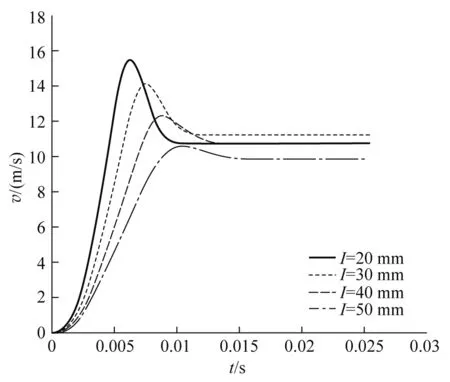
图9 不同发射电路状态时的弹体速度v和时间t关系曲线

4 结论

本文建立的单级磁阻型电磁发射模型，是在一定条件下的简化.虽然本模型具有一定的局限性，但能说明影响弹体发射速度的主要因素，可以为磁阻型电磁发射的参数优化提供参考.