二次量子化中单体和两体算符的一种启发式推导
吴 宁
(北京理工大学 物理学院 量子技术研究中心,北京 100081)
二次量子化是处理相互作用量子多体系统的重要理论工具,也是研究生和高年级本科生需要学习和掌握的重要内容.本刊仅有为数不多的几篇论文对此进行过相关讨论[1-3].根据笔者的教学经验,初学者往往较难全面理解如何从一次量子化中的多粒子哈密顿量及波函数出发,导出二次量子化中由产生和湮没算符表示的单体和两体算符这一关键步骤.
众所周知,自由经典电磁场由无穷多个相互独立的简谐振子描述,这使得玻色系统二次量子化表述的建立相对自然:只需将量子简谐振子(单模玻色子)的理论直接扩展至多模情形.在狄拉克的经典著作《量子力学原理》[4]一书中有对以上过程的详细阐述(见§60).这或许也是为何大部分量子力学教科书通常在引入Fock空间的概念后立即同时引入粒子的产生和湮没算符及其正则对易或反对易关系[5-8].诚然,这样做的动机源于量子谐振子代数解法中能量量子产生和湮没算符的引入.但对于多费米子系统,这多少显得有些突兀.笔者认为,量子谐振子的代数解法并不是建立二次量子化表述的必要知识.相反,对量子谐振子的提前了解甚至会导致一些不必要的混淆.例如,当考虑多个处于谐振子势中的全同费米子时,学生容易对以下事实产生混淆:单谐振子的能量量子产生和湮没算符满足单模玻色子的正则对易关系;而二次量子化中真实费米子的产生和湮没算符却满足正则反对易关系.
如Sakurai等人所著的《现代量子力学》[5]一书中所指出的,引入产生和湮没算符的正则对易或反对易关系是“非常专设的”(“very ad hoc”),且“不可能避开发展相对性量子场论而以最小化的人为假设为前提来建立一个完全自洽的处理”.
本文拟基于熟知的物理概念,通过严格的数学推理,以一种自洽且具有启发性的方式逐步引入粒子产生和湮没算符及其满足的正则对易/反对易关系. 该方法仅依赖于:多粒子波函数的对称化假设;Fock空间中“真空填充”的概念;以及全对称或全反对称多粒子波函数与Fock态的等价性.
基于以上3条事实,可自然地引入粒子的产生算符以及它们之间的对易/反对易关系. 为了进一步得到粒子产生和湮没算符之间的关系,注意到一次量子化中单体算符对全对称/反对称态的作用亦等价于二次量子化中相应单体算符对Fock态的作用.基于此,可同时自洽地得到产生和湮没算符之间的关系及二次量子化中单体算符的具体形式.
因多费米子波函数归一化操作的简单性,本文着重讨论全同费米子系统.但类似的方法亦可应用于全同玻色子系统.
1 全反对称态与Fock态的等价性
1.1 一次量子化表述概要
考虑一由N个全同费米子组成的相互作用多体系统.在一次量子化表述中,我们被迫要对全同粒子进行标号而将第i个粒子的单粒子态写为|φα〉i,其中希腊字母α表示单粒子态的指标.假设共有M个单粒子态.根据所考虑物理系统的不同,M可为一有限(如一个自旋-1/2粒子的两个自旋态)或无限大(如简谐振子的所有本征态)的整数.设这M个单粒子态{|φα〉i|α=1,2,…,M}组成粒子i的完备基,即
(1)
则N个费米子系统完备基为以下一系列张量积态:
|φP1〉1|φP2〉2…|φPN〉N
(2)
其中Pi∈{1,2,…,M}为粒子i所占据的单粒子态的指标.由于N个费米子是全同的,总可以选取粒子指标排序以满足1≤P1≤P2≤…≤PN≤M.以下我们称由式(2)给出的满足以上态指标排序的特殊乘积态为一参考态.
多粒子系统的一次量子化哈密顿量一般可写为
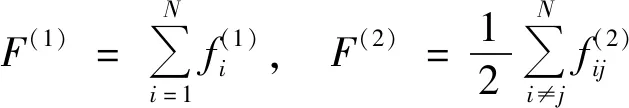
(3)
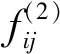
(4)
1.2 全反对称态
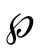
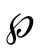
(5)
其中对π的求和遍历粒子指标{1,2,…,N}的所有N!个置换.若π为偶(奇)置换,则有σ(π)=1 (-1).对称性假设蕴含了泡利不相容原理,即式(5)中所有的态指标{Pi}必互不相同.由此可将参考态中态指标的排序加强为1≤P1<… (6) (7) (8) (9) 为此,必须对产生算符施加如下反对易关系: (10) (11) (12) (13) 初看起来式(13)的推导并不明显,这里对M=3,N=2的简单例子加以验证.由式(6)有 这与式(13)相符. |φQi〉i…|φPN〉N]= (14) 其中在最后一行中利用了对应关系(11).由式(12),我们期望上式右边等于 为此引入费米子湮没算符的如下性质: (15) 利用关系式(10)和式(15),容易证明等式 (16) 证明: 将式(16)代入式(14),得 比较上式与式(12)便得 (17) 至此,我们利用新引入的关系式(15)完成了对单体算符二次量子化形式的推导. 将上式中圆括号内的单粒子态展开并注意到矩阵元 仅与态指标有关,可得 利用式(10)和式(15),容易证明如下等式: 于是有 做指标代换Qi→α,Ql→β并将对i和l的求和扩展至所有单粒子态,得 再利用等式 〈φα|〈φβ|f(2)|φγ〉|φδ〉=〈φβ|〈φα|f(2)|φδ〉|φγ〉 将对γ和δ的求和对称化,并注意到γ=δ项的贡献为零,最终得到
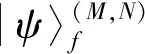
1.3 Fock态:真空填充


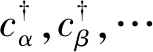
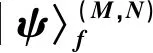
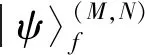
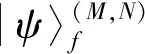
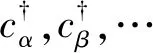
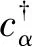
2 单体算符的推导:cα和之间的关系
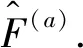
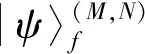
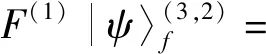

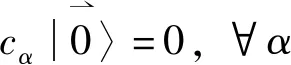
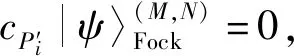
3 两体算符的推导:一个直接的扩展
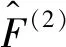

4 结论
——记上海交大领衔的科研团队成功捕获马约拉纳费米子的重大成果

