多源数据矩阵增量约简算法

徐岩柏，景运革

运城学院 数学与信息技术学院，山西 运城 044000

现实生活中，传感器技术发展促进了各行各业产生了大量多源数据（分布数据），如何发现多源数据中隐含的知识是人工智能方向研究的一个热点问题。近10多年来，一些研究者已经提出了许多处理多源数据的形式概念分析方法并运用它们去解决一些实际问题[1-3]。但是在现实生活中，多源数据大多都包含不确定性的信息，因此利用上述方法不能对多源数据进行精确化处理及数据分析和挖掘。

粗糙集理论为解决上述问题提供了一种新的技术方案，在没有任何先验知识的条件下，能够解决不一致和不精确多源数据知识挖掘和发现的问题。目前已经有很多研究者利用粗糙集理论和数据融合技术去处理多源数据知识挖掘的问题[4-8]。但这些算法对于静态多源数据是有效的。可是，如果用上述方法去计算动态多源数据约简的问题，因为不能有效利用原有的计算结果，导致求解动态分布数据约简就会花费很多时间，使得计算效率很低。为了克服上述静态算法的缺陷，一些研究者把增量学习技术应用到粒计算和粗糙集理论中。

增量学习技术可以充分利用原有的计算结果，避免重复计算，提高计算效率。目前很多学者把增量技术应用到求解信息系统约简的问题中。这些增量方法主要用来去计算信息系统对象、属性和属性值发生变化后的约简问题。首先，一些学者针对对象添加到信息系统后如何迅速计算其约简问题，提出了对象发生变化后的增量约简算法[9-11]。其次，另一些学者针对属性添加到信息系统后如何快速更新其约简问题，给出了信息系统增量计算机制，提出了属性发生变化后的增量约简方法[12-15]。此外，还有一些学者针对信息系统属性值发生改变后如何迅速获得其约简问题，提出了属性值发生变化后的增量约简算法[16-18]。综上分析，虽然研究者提出了很多增量约简算法，但是这些方法主要用来解决单个信息系统数据动态变化后的约简问题，而利用增量技术解决动态多源数据约简的方法却报道鲜少。因为多源数据来源于不同地方，如何探讨多源数据之间及多源数据与增加数据之间的内在联系及数据如何有效融合是计算动态多源数据约简中的一个难点问题。因此，当分布数据增加了一些属性后，本文提出了基于分布数据的矩阵增量约简算法，可以快速实现动态多源数据的融合，计算动态多源数据的约简。

1 基于知识粒度分布信息系统约简算法

本章简单介绍分布信息系统相关概念和定义及分布数据约简的方法[19-20]。

1.1 分布信息系统的基础知识

定义3给出一个分布信息系统DS=(U,A,V,F)=中任意两个独立的子信息系统S i和S j的关系矩阵为，则DS的知识粒度定义如下：

1.2 分布信息系统非增量约简算法

2 分布决策信息系统增量约简算法

2.1 分布决策信息系统增量机制

2.2 分布系统属性增加的矩阵增量约简算法

2.3 时间复杂度分析

3 仿真实验方案

3.1 实验软硬件环境和实验数据集

为了验证本文所提出的矩阵增量约简算法在获得动态多源数据约简时具有很强的计算性能，本文分别用矩阵增量和非增量约简算法做了一些对比仿真实验，并从机器学习网站下载实验所用到的UCI数据集，数据集具体描述如表1所述，由于下载的UCI数据是单源数据，为了模拟多源数据实验环境，把下载的实验数据分成不同部分，这些不同部分数据在实验中表示多源数据，本文为了实验的简单性，把实验数据分成3部分的多源数据。另外，实验所用到的软件及硬件配置描述如表2所述。

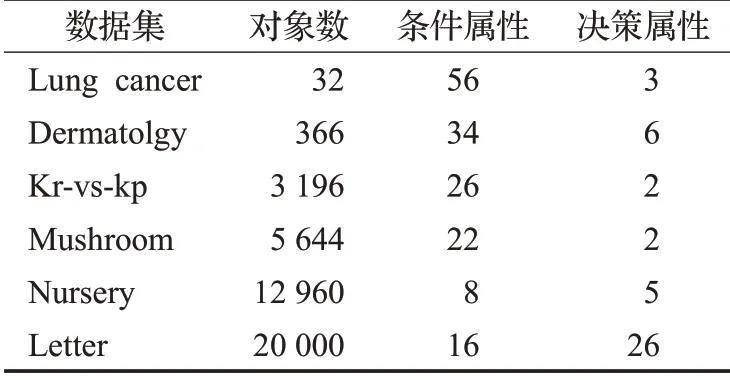
表1 UCI数据集描述Table 1 Description of UCI date sets

表2 软件和硬件配置描述Table 2 Description of computer software and hardware configuration

3.2 属性约简结果比较

在对比实验过程中，首先把表1中所有数据按照条件属性分成大小相等的两个数据集，把其中一个数据集按照对象的40%、30%、30%分成3个数据集，作为实验中的多源数据，把另一个数据集按照属性的20%、40%、60、80%、100%分成5个数据集，作为增量的属性集，依次把这些属性添加到分布信息系统所有的子信息系统中，然后分别用矩阵增量和非增量约简算法对它们进行测试，两种方法计算约简的运行时间如图1中每个子图所示，图1中所有子图的X轴表示增量属性集的大小，Y轴表示运行时间，矩阵非增量和增量约简算法的运行时间分布用圆形蓝色和方形红色的线表示。

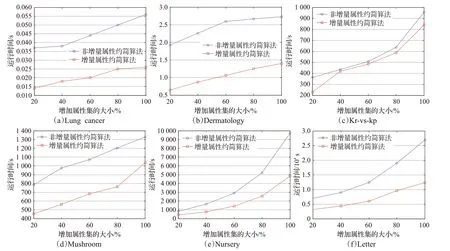
图1 增量及非增量约简算法的计算时间结果比较Fig.1 Comparison between incremental reduction method and non-incremental reduction method on computation time

从图1结果可知，矩阵增量计算动态多源数约简的运行时间远远小于非增量约简算法的运行时间，特别是对于较大数据集而言，增量约简算法的计算性能优势更加明显，说明了增量约简算法能够提高计算动态多源数据约简的效率。

3.3 属性约简分类精确度分析比较

为了验证矩阵增量算法在计算动态多源数据约简是有效的，本节先把表1中6个UCI数据集依照属性集分成均匀两个数据集，把其中一个数据集按照对象的40%、30%、30%分成3个数据集，作为实验中的多源数据，把另一个数据集作为属性增量数据集，并把其添加到分布信息系统所有子信息系统中，然后分别利用矩阵增量和矩阵非增量约简算法去计算变化后多源数据的约简。并通过贝叶斯分类及10折交叉验证算法去计算矩阵增量和矩阵非增量约简算法所获得属性约简的分类精确度，在实验过程中，把多源数据集随机分成10份，其中9份用以训练，另外1份用以测试。为了使实验结果更具有代表性，所以测试过程重复10次，每次用不同数据进行测试。计算的分类精确度结果如表3所示。

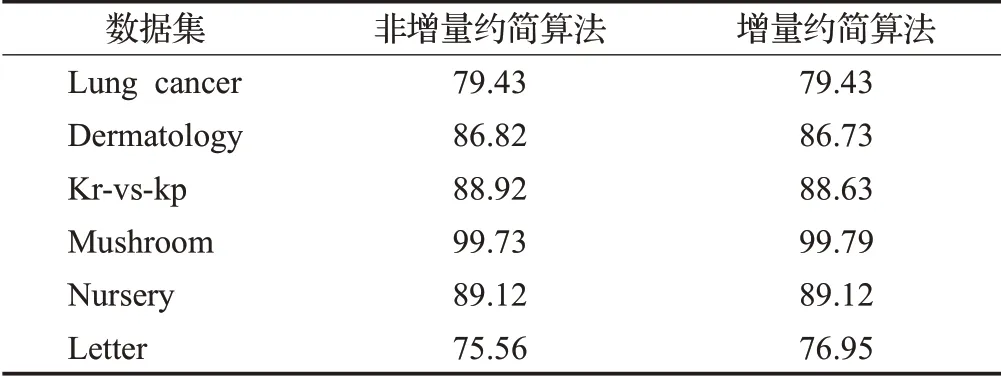
表3 比较增量及非增量属性约简分类精确度Table 3 Comparison of incremental reduction method and non-incremental reduction method on classification accuracy%

从表3结果可以看出，矩阵增量和矩阵非增量约简算法计算所得约简的分类精确度是非常相近的，说明分布信息系统增量约简算法不仅可以快速找到动态分布信息系统的约简，而且在处理动态分布信息系统属性约简的问题具有较强的计算性能。

4 结束语

总结了分布信息系统的矩阵增量约简算法的主要特点、涉及到的相关内容及未来研究方向如下：

（1）给出了分布信息系统等价关系矩阵融合的方法及动态多源数据等价关系矩阵增量融合技术。

（2）当一些属性增加到分布信息系统后，讨论了多源数据增加属性后的分布信息系统的增量机制和定理。

（3）在分布信息系统增量机制和定理的基础上，提出了多源数据矩阵增量约简算法。

（4）分别利用矩阵增量和非增量约简方法对UCI数据集进行对比测试，实验结果验证了矩阵增量约简算法在运行时间上远远优于非增量约简算法，且两种方法所得到的分类精确度是非常相近的。

（5）由于多源数据对象集和属性集也会同时发生变化，如何设计多源数据对象集和属性集同时变化后的矩阵增量属性约简算法是未来研究方向。