基于信任关系的TODIM群体多属性决策方法

刘议聪，楚俊峰，2，王燕燕

1.福州大学 经济与管理学院，福州 350108

2.福州大学 决策科学研究所，福州 350108

3.福建农林大学 公共管理学院，福州 350002

多属性决策问题就是根据专家对各个方案的不同属性做出的评价结果，决策者对方案进行排序和择优，在社会中各领域都有着广泛的应用[1-4]。多属性决策具有多种类型[5-16]，依托决策信息类型的多属性决策主要包括模糊决策[5]、直觉模糊多属性决策[6-9]、语言多属性决策[11，13-14，16]、犹豫信息和犹豫语言多属性决策[15-16]、区间值信息多属性决策[11]等。传统的多属性决策模型建立在期望效用理论基础上，但实际生活中，由于自身处理信息能力的限制、信息的不完全等因素导致决策者进行决策时不可能保持完全理性，此时做出的决策可能会对最终结果产生影响，并造成损失[17]。

基于前景理论的TODIM决策方法作为多属性决策方法之一，得到了许多学者的关注，并相继取得了一些成果。樊治平等[18]针对考虑决策者心理行为的区间数多属性决策问题，提出一种基于TODIM的决策分析方法。姜艳萍等[19]考虑到决策者具有参照依赖和损失规避行为，提出了一种基于不完全信息的TODIM决策方法。张永政等[20]考虑到决策者的不同偏好和心理行为，提出了基于概率语义术语集的TODIM多属性决策方法。上述针对TODIM决策问题的研究，大多都将专家视为相互之间没有关系的独立个体，忽略了专家之间的社会网络关系，但是在现实的社会网络中，专家并不是完全独立的个体。因此，许多学者针对社会网络中的个体进行了研究。

Wu等[21]提出了在不完全语言信息背景下的社交网络信任共识模型，利用专家之间的信任关系来对不完全信息进行估计。Wu等[22]将社交网络和基于协同过滤的信任关系结合，提出了一种群体决策（GDM）中不完全信息的综合估计方法。Wu等[23]在基于四元组信息的社会网络中引入一个信任传播算子来获得一个完整的社交网络，从而在节点之间产生信任关系。Liu等[24]提出了一个新的基于关系强度的信任传播算子来构建一个完整的社会网络。Wu等[25]和Liu等[26]研究了一种基于信任的推荐机制，通过获得的信任关系生成推荐建议。Perez等[27]利用从专家社会网络收集的语言可信度信息来集结社会群体的偏好，从而获得最适合方案的选择。Recio等[28]针对群体的决策支持系统，提出了代表群组内的社会联系的多代理架构。现有的有关信任的研究都是利用信任关系来帮助专家对需要被评价方案的相关信息进行协同过滤，根据协同过滤之后的信息进行综合，最后对方案进行评价与决策。

通过上述分析，针对现有研究存在的不足之处，本文提出了基于信任关系的TODIM群体多属性决策方法。根据专家的信任网络，以信任度最高的专家的评价矩阵以及自身的信任程度来对自己的评价矩阵进行修改，再运用TODIM决策方法获得方案的排序结果，有助于提高群体决策矩阵的最终排序结果的可信度。该方法不仅能充分结合社会网络群体中的信任关系，还可以保证原始评价数据，以尽可能少的成本保证决策效率。

1 基本知识

1.1 信任关系相关知识

信任网络就是社会网络中的专家构建信任关系，并将这些信任关系构成网络，这样的网络称作信任网络[29]。

定义1（信任得分）信任得分(t,d)是集合[ ]0,1×[ ]0,1中的元素，其中，t是信任程度，d是非信任程度。信任关系矩阵可以用TD=[(t uv,d uv)]r×r来表示，(t uu,d uu)=(1,0),u，v=1,2,…,r，φ表示元素(t uv,d uv)空缺，则：

定义2[25]（Einstein积算子、Einstein和算子）Einstein积算子E⊗以及Einstein和算子E⊕被用来说明信任传播的一般方法。

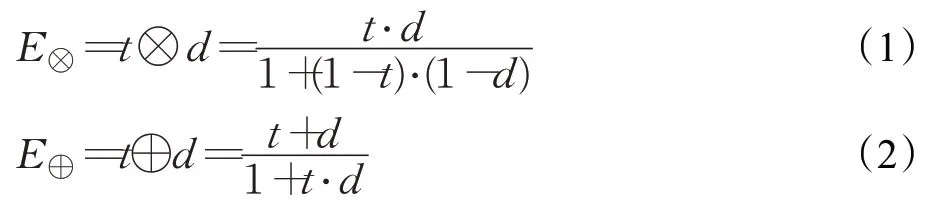
定义3[25]（对偶信任传播算子）针对信任网络中的(t1,d1)和(t2,d2)，那么对偶信任传播算子Z可以定义为：

Z((t1,d1),(t2,d2))=(E⊗(t1,t2),E⊕(d1,d2))=

当信任网络中的专家数量不少于两个时：

Z((t1,d1),(t2,d2),…,(t r,d r))=(E⊗(t1,t2,…,t r),

信任关系的属性：

（1）传递性：指专家A对专家B直接信任，专家B对专家C直接信任，则专家A对专家C间接信任，如图1所示，传递公式如式（5）：

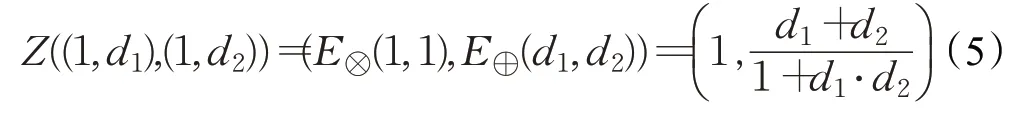
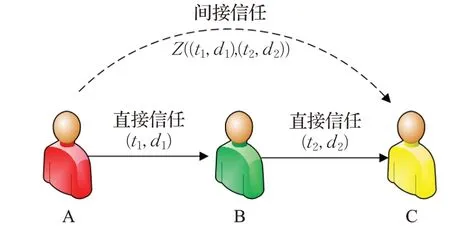
图1 信任关系之间的传递性Fig.1 Transitivity between trust relationships

（2）不对称性：由于信任网络是加权有向图，所以会出现专家A信任专家B，但专家B不信任专家A，如图2所示。

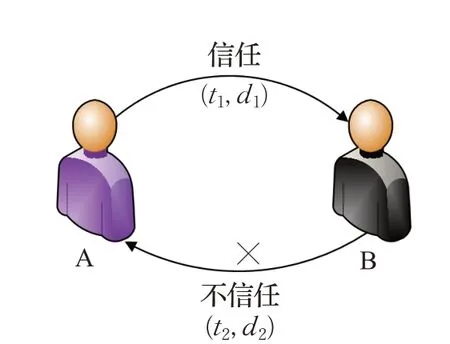
图2 信任关系的不对称性Fig.2 Asymmetry in trust relationships

1.2 TODIM群体多属性决策方法

2 基于信任关系的TODIM群体多属性决策模型

在社会网络中，专家可以构建自己与社会网络中其他人的信任关系[22，24-26]。专家选择最信任的人，并依据信任者的决策矩阵来对自己的决策矩阵进行修改，可以提升最终方案总优势度的一致性，方便决策者对备选方案进行排序和择优。

在社会网络中，TS值可以作为专家重要度的可靠来源，即：专家的TS值越高，该专家的意见就越重要。因此在信任网络中，TS值最高的专家就是领导者。比较大小可得，，即专家el的TS值最高，e l为该信任网络的领导者。

步骤1根据式（1）~（4），社会网络中的专家建立信任关系，得到各专家的(t,d)、TD矩阵以及评价矩阵

步骤2根据式（6）、（13），得出各专家的TS值以及信任网络中的领导者el。针对不了解的元素，专家根据领导者的决策矩阵对自己的矩阵进行修改，并进行规范化，规范化矩阵为

步骤3根据式（9），计算属性c j相对于属性c r的相对权重。

步骤4由式（10）计算领导者e l针对属性c j方案Ai相对于方案A k的优势度。对于专家e u(e u∈E，u≠v)针对属性c j方案Ai相对于方案A k的优势度，其计算公式为：

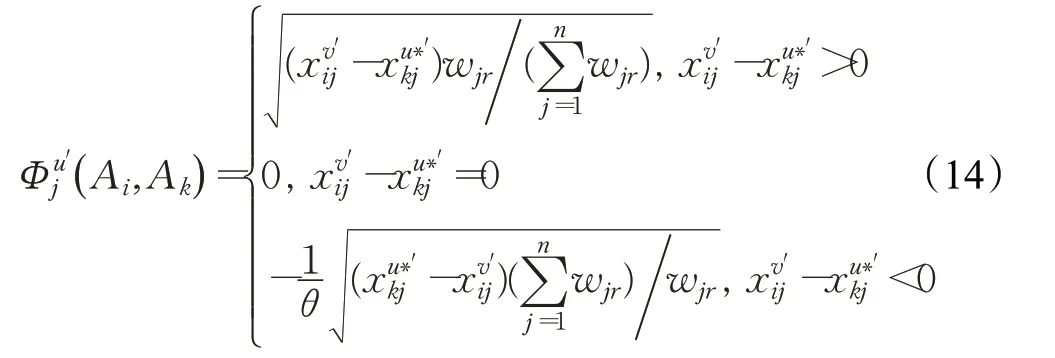
步骤5由式（11）可得出领导者el以及专家e u关于方案A i相对于方案A k的综合优势度。但对于专家e u等而言，在计算综合优势度时不仅要考虑信任关系，还希望保留自己的原始评价因素。这种希望的程度被专家自信所影响，故本文引入自信程度α，α∈[ ]0,1，判断α及取值对最终结果的影响，其计算公式为：

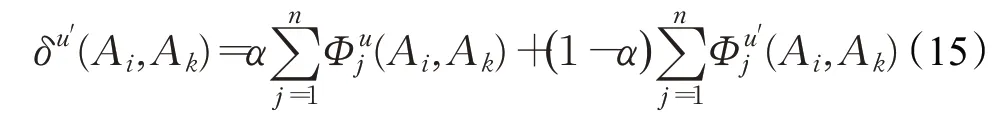
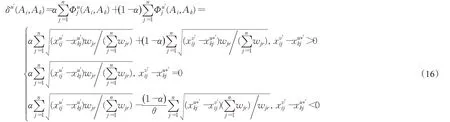
当时：

xu′ij-x u′kj＜0

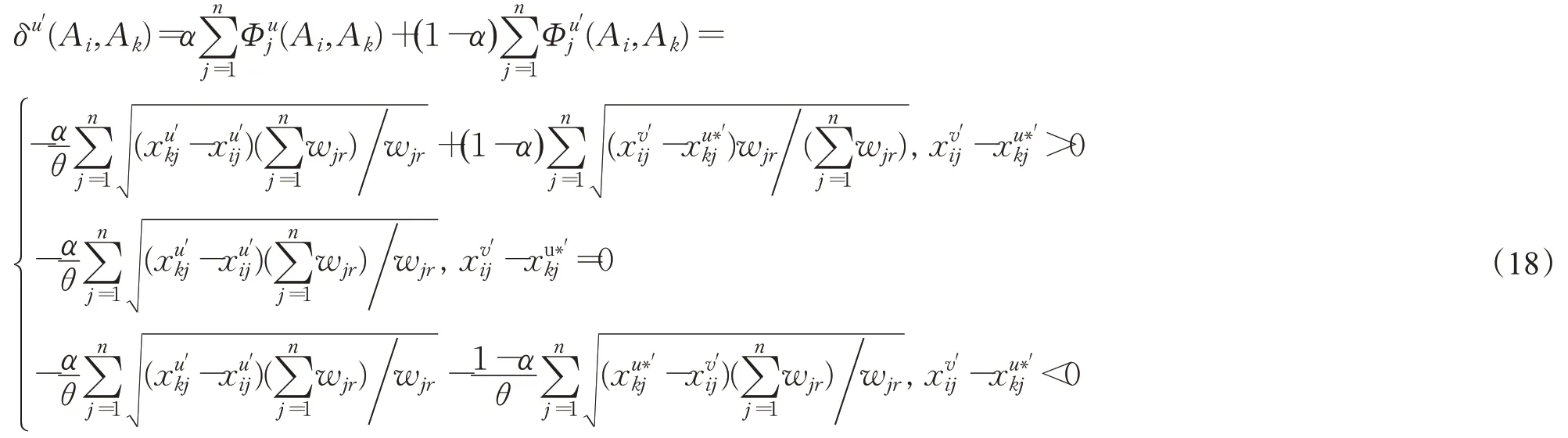
当α=0时，此时领导者el的综合优势度矩阵完全取代了e u的综合优势度矩阵；当α=1时，e u的综合优势度矩阵保持不变。通过对α值进行灵敏度分析来判断专家如何在信任关系和自身独立性之间保持平衡。

步骤6专家e u针对方案Ai相对于其他所有方案的总体优势度，其计算公式为：

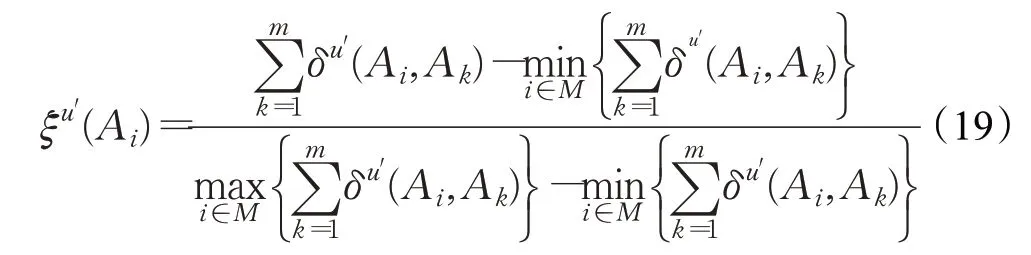
并根据总体优势度结果对方案进行排序。

步骤7由式（7）计算出各专家在社会网络中所占权重，根据式（8）、（10）~（12），计算出群体决策矩阵，进行规范化后计算出相应的方案总体优势度，并进行方案排序，ξu′(A i)越大，方案A i越优。

步骤8结束。

3 算例分析与讨论

3.1 算例

农产品由于品种繁多、数量庞大且对销售渠道功能要求高，因此在选择农产品供应商时需要进行群体决策。本文考虑一个农产品供应商选择问题。某公司需要从六个供应商A1~A6中选择其中两个农产品供应商进行供货，为了能使本公司利益最大化，该公司邀请五位专家e1~e5分别对A1~A6提供的六个方案从服务水平c1、品牌价值c2、成本c3、质量c4、供应能力c5、市场前景c6等六项属性进行评价，本文假设属性的权重向量为w=(0.1,0.15,0.2,0.25,0.2,0.1)T。各专家针对备选方案的判断信息以矩阵的形式给出。专家e1~e5之间的信任网络如图3所示。

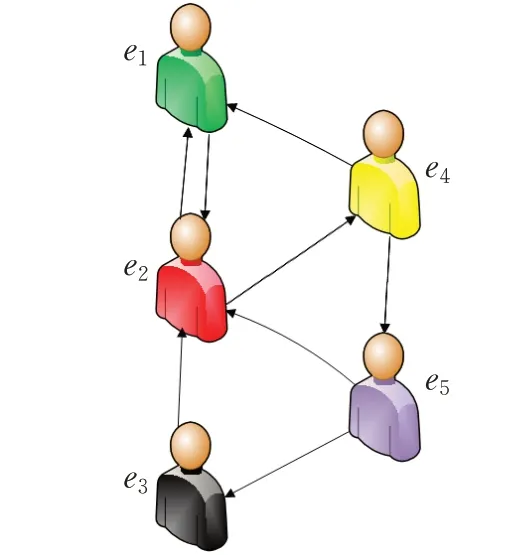
图3 专家e1,e2,e3,e4,e5之间的信任网络Fig.3 Trust network between e1,e2,e3,e4,e5

步骤1根据式（1）~（4），社会网络中的专家建立信任关系，得到各专家的(t,d)、TD矩阵以及评价矩阵

步骤2根据式（6）、（13），得出各专家的TS值以及信任网络中的领导者el。针对不了解的元素，专家根据领导者的决策矩阵对自己的矩阵进行修改，并进行规范化，规范化矩阵为

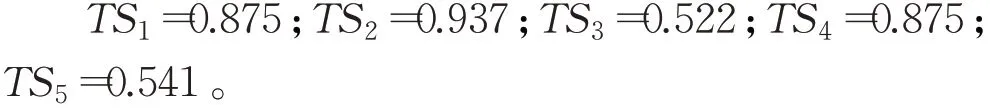
步骤3本文假设属性c1~c6的权重为w=(0.1,0.15,0.2,0.25,0.2,0.1)T，根据式（9），则此时的wr=0.25，各属性的相对权重为( 0.4,0.6,0.8,1,0.8,0.4)T。

步骤4由式（10）计算领导者e2针对属性c j方案Ai相对于方案A k的优势度。对于，由式（14）计算其余专家e u（e u∈E，u≠v）针对属性c j方案Ai相对于方案A k的优势度。在已有的关于TODIM的研究中，θ=1和θ=2.5这两个取值最多被采用。在本研究中，选取衰减因子θ的值为1。以专家e3针对属性c1为例进行计算，结果如表1所示。其余属性同理。

表1 专家e3针对属性c1时方案Ai对A k的优势度Table 1 Superiority of scheme Ai over Ak when expert e3 targets attribute c1

步骤5结合表1等，根据式（15）~式（18），计算方案A i相对于方案A k的综合优势度。此处取α=0.1。结果如表2所示。

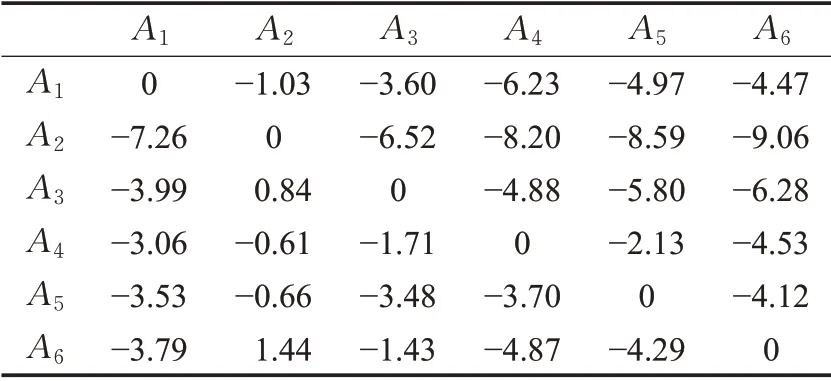
表2 专家e3针对方案Ai对Ak的综合优势度Table 2 e3’s comprehensive superiority of scheme A i over A k

步骤6计算方案总体优势度并排序。根据表2的数据，以及式（19），获得专家e3对方案的总体优势度。结果如表3所示。

表3 专家e3对方案的总体优势度Table 3 Overall superiority of expert e3 to scheme

步骤7由式（7）可得专家e1~e5在信任网络中所占权重分别为w1=0.23；w2=0.42；w3=0.1；w4=0.13；w5=0.12。根据式（8）、（10）~（12），计算出群体决策矩阵xˉ′，相应的方案总体优势度如表4所示。

表4 基于信任关系的群矩阵对应的总体优势度Table 4 Overall superiority corresponding to group decision matrix based on trust relationship

根据式（8）计算基于信任的群体决策矩阵：

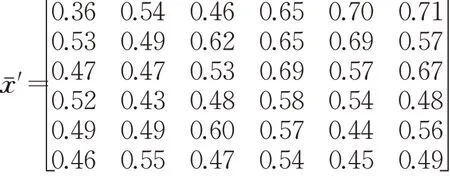
方案排序结果为A2≻A3≻A1≻A5≻A4≻A6，此时决策者应选择的供应商为A2、A3。

步骤8结束。

3.2 分析讨论

为了说明本文所提出的基于信任关系的TODIM群体多属性决策方法的合理性和有效性，下面使用TODIM群体多属性决策方法对以上算例进行求解，进行对比分析，并对自信程度α进行灵敏度分析。

3.2.1 对比分析

采用未考虑信任关系情境下的TODIM群体多属性决策方法处理算例3.1中的问题，计算结果如下：

此时的群体决策矩阵为：

如表5所示，相应的方案总体优势度如方案排序为A2≻A1≻A3≻A5≻A4≻A6。

表5 基于TODIM的群矩阵对应的总体优势度Table 5 Overall superiority corresponding to group decision matrix based on TODIM

通过对比分析，采用未考虑信任关系情境下的TODIM群体多属性决策方法，此时决策者应该选择的供应商为A2、A1。而采用本文提出的方法，通过计算，A3的总体优势度变化不显著，而A1的总体优势度变化显著，且此时决策者选择的供应商为A2、A3。

3.2.2 灵敏度分析

为了解专家的自信程度α对专家方案排序结果产生的影响，将对α值进行灵敏度分析，显示了对不同α值对专家排序结果的具体细节。如图4~图6所示。

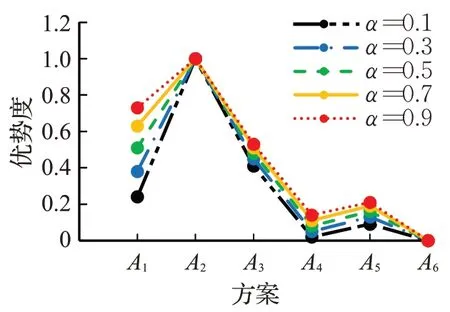
图4 α值对e3排序结果的影响Fig.4 Effect ofαvalue on sorting result of e3

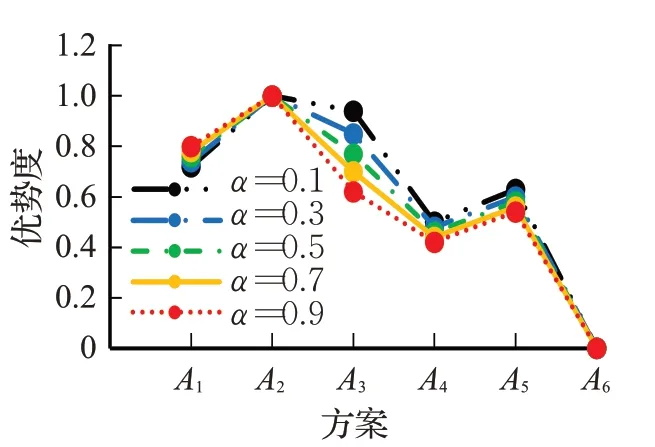
图6 α值对e5排序结果的影响Fig.6 Effect ofαvalue on sorting result of e5

由上述图表可知，当α=0.1时，专家e3、e4、e5对各方案的排序结果均为A2≻A3≻A1≻A5≻A4≻A6，群体方案排序保持不变。当α=0.5、0.7、0.9时，e3的排序结果改变；当α=0.3、0.5、0.7、0.9时，e4的排序结果变化；当α=0.7、0.9时，e5的排序结果变化。

对于专家e3、e4，当α=0.1时，专家选择的供应商为A2、A3；当α=0.3、0.5、0.7、0.9时，专家选择的供应商为A2、A1。对于专家e5，当α=0.1、0.3、0.5时，专家选择的供应商为A2、A3；当α=0.7、0.9时，专家选择的供应商为A2、A1。因此，在群体决策中选择合适的α值可以更好地帮助决策者得出适合于本组织的方案。

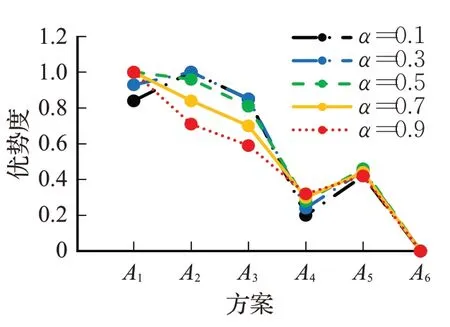
图5 α值对e4排序结果的影响Fig.5 Effect ofαvalue on sorting result of e4

由算例分析及其排序结果可知，决策者应该选择的供应商为A2、A3。采用未考虑信任关系情境下的TODIM群体多属性决策方法（3.2.1小节），专家e1~e5得出的排序结果不一致，且群体决策矩阵相对应的最终排序结果与TS值最高的专家e2也不一致。而本文提出的基于信任关系的TODIM群体多属性决策方法（3.1节），当专家e3、e4、e5根据信任关系修改了自己的评价矩阵，最终排序结果均为A2≻A3≻A1≻A5≻A4≻A6，提高了最终决策结果的可信度，帮助决策者选出最符合本公司利益的方案。

由于最终决策结果具有不一致性，在算例3.2.1小节中，直接使用TODIM群体决策方法时，为了降低这种不一致性，每个专家都需要对自己的评价矩阵进行迭代调整，耗时过长，提高了调整成本。而在算例中，在建立信任网络之后，部分专家可以直接根据信任专家的评价矩阵对某些元素进行调整，这样不仅保持了自己的原始判断信息，还降低了时间成本以及人力成本，以尽可能少的成本保证最终决策结果的一致性，提升了决策效率。

当专家利用信任关系对方案进行评价时，或多或少地会存在主观意识，这种主观意识形成了自信程度，即α。因此需要确定当α值在某一个范围内变化时，评价的结果将会产生怎样的变化。从3.2.2小节中可以看出，当α=0.1时，e3,e4,e5的排序结果均与e1,e2一致，且与最终群体方案排序一致。当α取0.3、0.5、0.7、0.9等值时，排序结果发生了变化，最终群体方案排序也不一致，这就为决策者选择最适合本组织的方案造成影响。

当基于大规模群体时，由于该群体的复杂性，本文提出的基于信任关系的TODIM群体决策方法并不能帮助决策者完全解决问题，未来还有待改进。但是在适当规模的群体中，该方法可以充分利用信任关系来帮助决策者选择最适合本组织的方案。

4 结论与展望

本文针对多属性决策问题，考虑到社会网络中的信任关系，提出了一种基于信任关系的TODIM群体决策方法。该方法从专家所处的社会网络出发，为专家建立信任关系，找到信任网络中TS值最高的专家，针对自己无法做出合理判断的方案或属性，可以根据该专家的评价矩阵来修改自己的评价矩阵。但是在这种信任关系中，专家的自信程度也会对评价值产生影响，合理的α值可以使专家的排序结果与最终排序结果保持一致。这种方法提高了最终决策结果的一致性以及可信度，弥补了由于专家的有限理性以及对方案不充分的了解带来的弊端，提高了专家的决策效率，而且保持了自己的原始判断信息，以尽可能少的成本保证最终决策结果的一致性，有效地帮助决策者对备选方案进行排序和择优。该方法为考虑社会网络中专家之间关系的TODIM多属性决策问题提供了一种新的解决途径。在未来的研究中，可以考虑在大规模群体中运用基于信任关系的TODIM群体决策方法。