基于子空间聚类的协同过滤推荐算法

王英博，韩国淼，王铭泽

1.辽宁工程技术大学 创新实践学院，辽宁 阜新 123000

2.辽宁工程技术大学 软件学院，辽宁 葫芦岛 125105

3.南宁学院 会计学院，南宁 530200

随着社会信息化进程的加快以及大数据时代的到来，互联网产生的数据量也在逐渐增多，为了帮助用户在海量数据中找到自身需要的数据，大量研究者和学者对相关方案进行了探索，由此推动了推荐技术的发展，广泛成功地应用于电子商务、视频网站以及社交网络等各个领域[1]。并且它也逐渐成为了各个网络平台必不可少的核心部分，力求为用户提供最优的决策支撑与信息服务，个性化推荐不需要用户提供详细的需求，而是仅仅根据用户的兴趣爱好以及历史需求来向用户推荐感兴趣的信息和商品。

推荐算法主要有基于协同过滤的推荐、基于内容的推荐以及基于关联规则的推荐。其中，基于协同过滤的推荐算法是推荐系统中应用最为广泛和成功的推荐算法，根据用户项目评分矩阵，寻找与目标用户有相似偏好的其他用户，即为目标用户的最近邻居，根据最近邻居进行项目评分预测，进而形成推荐列表。传统的协同过滤推荐算法是在整个用户空间中搜索目标用户的最近邻居，这明显非常耗时，以及也存在寻找的邻居不合理的情况，进而导致推荐质量和效果差等问题[2]。

针对上述情况，很多研究学者提出了改进的协同过滤推荐算法。陈建瑞等[3]提出了基于双层网络的动态聚类协同过滤推荐算法，其基于用户和物品的属性信息建立用户层和物品层网络，并结合层次聚类算法来改进推荐算法，进而提高推荐质量。张文龙等[4]利用用户历史的交互学习中学习用户偏好，提出了基于双重最相关注意力网络的协同过滤推荐算法。唐泽坤等[5]考虑用户模型的数据密度、距离以及用户活跃度，并结合改进的Canopy聚类来改进推荐算法。顾明星等[6]将KMeans++算法与协同过滤算法相结合，并改进用户间的相似性计算方法，以此来提高推荐算法的效率和质量。高仰等[7]提出了融合知识图谱和短期偏好的推荐算法，其将知识图谱的三元组关系引入到推荐算法中，改善了推荐算法的性能。李维乾等[8]提出了一种多属性条件受限的波尔兹曼机协同过滤模型，也使推荐效果得到了一定的提升。王永贵等[9]提出一种优化聚类的协同过滤算法，其利用花朵授粉算法来优化K均值聚类算法，以此来增强聚类效果，改善推荐质量。Tsai等[10]提出了一种聚类集成的协同过滤算法，其将K-Means和SOM算法集成在一起来改善推荐算法的性能。综上所述，由于传统的基于用户的协同过滤算法主要存在冷启动和数据稀疏性两个主要缺点，所以，所有的改进算法基本都是针对这两方面进行优化。很多学者都针对数据稀疏性的缺点提出了自己的改进方法，通过对上述文献的阅读，针对其改进的方法主要有以下几种：（1）通过KMeans等聚类算法对其进行聚类，以寻求降低数据的稀疏性。（2）融合用户偏好以及信任关系来缓解数据稀疏性。（3）利用填充算法缓解数据稀疏性。（4）通过自动编码器构建神经网络协同过滤模型。当面对数据高维问题时，目前的改进方法大多数是通过SVD、PCA等算法对数据降维，以此来处理该问题。在利用K-Means等聚类算法来优化推荐算法时，通常都要考虑聚类簇数，不同的类簇数获得的推荐效果不同。其次，在利用降维算法解决数据的高维问题时，算法的时间复杂度也会随之增加。

本文针对数据的稀疏性和高维性对推荐算法性能影响的问题，提出了一种基于子空间聚类的协同过滤推荐算法，该算法通过构建用户在Interested、Uninterested以及NN-interested三种类别下的项目子空间来寻找用户的最近邻居，然后利用项目子空间为目标用户绘制邻居用户树。聚类过程和子空间的构造过程是在用户离线阶段完成，当用户进入时，就会直接在线为其提供推荐列表，这个是其优势之一，此外，提出了一种新的用户相似度计算方法。实验验证表明，本文提出的算法在一定程度上能够提升推荐算法的性能。

1 传统协同过滤推荐算法

传统协同过滤算法的基本步骤是：首先利用已有的用户历史行为数据信息，构建用户-项目评分矩阵，然后通过相似度计算公式计算用户之间的相似度，选取相似度较高的用户作为目标用户的近邻集，最终在进行评分预测后按照TOP-N原则对用户进行推荐[11]。

1.1 构建用户项目评分矩阵

构建用户项目评分矩阵R m×n，在此矩阵行中有m个用户，用U表示，U={u1,u2,…,u m}，矩阵列中有n个项目，用I表示，I={i1,i2,…,i n}，R ij表示用户i对项目j的实际评分，若用户i对用户j未评分，则Rij为0，用户项目评分矩阵公式如下所示：

1.2 用户评分相似性计算

用户评分的相似性计算以用户项目评分矩阵为基础，将评分矩阵中的每一行的评分向量来表示用户的实际兴趣。所以，计算用户评分的相似性实质上就是计算用户评分向量之间的距离[12]。传统的协同过滤算法中通常使用的计算相似性的方法有3种，分别为Pearson相关系数、Jaccard系数以及余弦相似性系数，但是最常用的是皮尔逊相似度计算方法。计算公式如下：

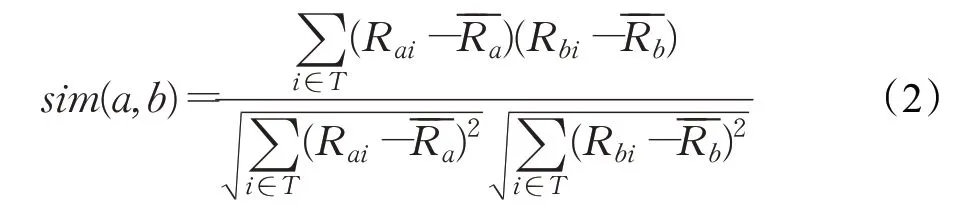
在获得用户a与所有用户的相似度后，将相似度最高的前h个用户作为其近邻集，最后应用评分预测公式得出最终的预测评分。预测评分公式为：

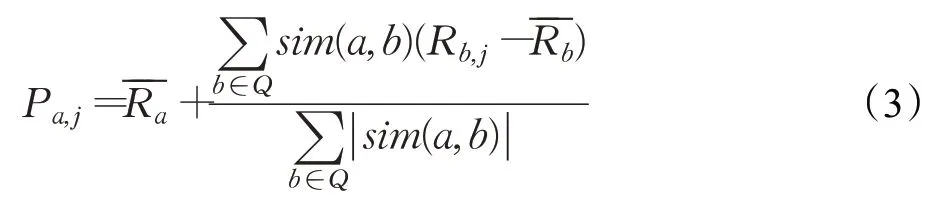
其中，P a,j表示用户a对项目j的预测评分，Q表示项目a的近邻集。

2 基于子空间聚类的协同过滤推荐算法

基于用户的协同过滤推荐算法在面对稀疏的数据集时，推荐质量会明显降低，并且随着大数据时代的到来，高维数据也越来越多，其也成为推荐算法所面临的挑战之一。在协同过滤推荐算法中，由于数据稀疏性，具有相似偏好的用户被认为是相似用户或邻居用户，反之，没有相似偏好的用户则不会被当作邻居用户。但是以后其也会有因为其他中间用户而使其成为邻居用户的可能[13]。其次，在传统或一些其他改进的协同过滤推荐算法中，邻居的数量或聚类数是变量，是需要通过调整来进行手动确定的。为此，本文提出了基于子空间聚类的协同过滤推荐算法。该算法利用新的数据表示方法，通过将主评分矩阵转化成三个二进制矩阵，通过处理三个二进制矩阵，进而得到项目列表，最终根据项目列表获得项目子空间，利用不同的项目子空间为目标用户生成三棵邻居用户树，进而寻找邻居用户。算法的流程如图1所示。

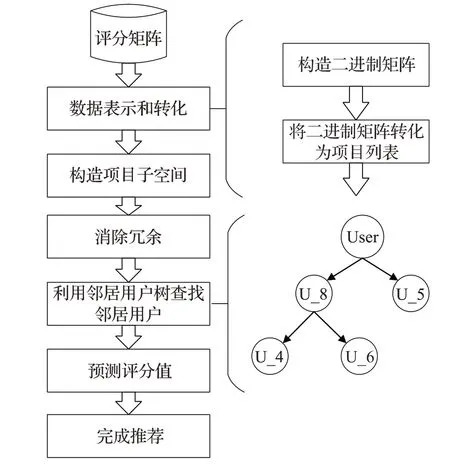
图1 推荐算法流程图Fig.1 Flow chart of recommendation algorithm

提出的算法的第一步就是提出了新的数据表示方法，以此来减少数据维数，并且，这种数据表示方法能够在很大程度上提升评分预测的计算过程的效率。下面将分别介绍流程中的每个过程。

2.1 数据的表示和转化

数据的表示和转化主要包括二进制矩阵的构造和将二进制矩阵转化为项目列表两个过程，根据用户-项目评分矩阵，将其划分为Interested、Uninterested以及NN-interested项目三个二进制矩阵，根据用户对项目的评分范围以及被推荐类别的电影等级，本文选择将评分为4和5的项目作为用户的感兴趣项目，并设置其值为1，其余设置为0，将其构造成第一个感兴趣项目的二进制矩阵[14]。同理，将用户评分值为3的项目作为用户的NN-interested项目，设置其值为1，其余设置为0。评分值为1和2的作为Uninterested项目，最终将用户-项目评分矩阵转换成三个二进制矩阵。具体二进制矩阵转化过程如图2所示。

如图2所示，用户-项目评分矩阵被转化成三个二进制矩阵，其中*代表为未作出评价的项目。提出上述数据表示方法的原因如下：（1）用户-项目评分矩阵包含了用户与项目之间的所有信息，并且其中也包含一些无用的信息，由于本文目的是通过寻找项目的子空间来进而找到目标用户的邻居用户，例如当项目数为n时，将会有2n个项目子空间，当面对项目数较多的数据集时，其空间复杂度会很高，所以要寻找到只包含有用信息的数据表示，以此来降低空间复杂度。（2）通过二进制矩阵可以获得相对应的项目列表，这种数据表示方法可以减少数据维数，并且由于三个二进制矩阵共同构成了用户项目评分矩阵，它们之间存在着互为包含的数据关系，所以当用户评分数据增加时，只需根据用户的评分处理相应的二进制矩阵即可，运算方便。

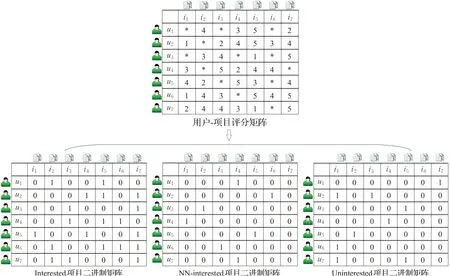
图2 二进制矩阵转化过程Fig.2 Transformation process of binary matrix

下面是将项目的二进制矩阵转化为项目列表的过程，由于三个二进制矩阵转化为项目列表的过程相同，所以，将仅以Interested项目为例，描述其转换过程和结果。Interested的项目列表如图3所示。

图3 Interested项目列表Fig.3 List of interested projects

2.2 构造项目子空间

这个过程是将获得的项目列表转换成项目子空间，并消除冗余项目，得到最终的项目子空间，用来寻找相似用户。仍然以感兴趣项目列表为例，寻找其项目子空间的方法如下：每个用户的感兴趣的项目子空间通过比较该用户与其他用户感兴趣的项目来创建，例如，对于用户ui，需要与用户(u i+1,ui+2,…,u m)分别进行比较，并且为了保存用户的局部子集，需要一个局部表，在迭代结束后，每个用户的数据都将被放入一个全局表中。对于Interested项目列表，如果寻找从用户u1开始，需要比较u1与用户u2，寻找两个用户的交集，得其交集为i3，然后，将i3加入到局部表中，然后比较用户u1和u3，交集i2加入到本地表中，用户u1和u4的交集(i2,i3)也被存入到局部表中[15]。当用户u1和u5交集(i2,i3)，相同的交集已经出现在表中，则更新计数值。当用户u1遍历比较完毕后，此时局部表中存在i2、i3和(i2,i3)3个条目，此时将局部表中的条目放入到全局表中，局部表中的内容被清除，全局表只接收全局表中不存在的条目。所以，当所有用户遍历完成时，全局表中不会出现重复的条目。Interested项目列表对应的初始项目子空间如图4所示。

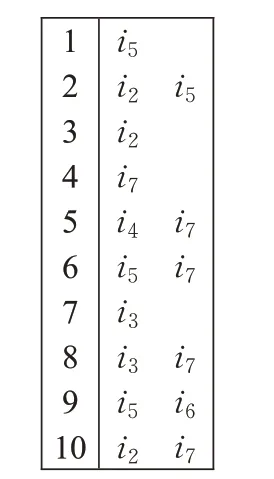
图4 Interested项目子空间Fig.4 Interested project subspace

创建项目子空间的算法过程如下：

算法1寻找Interested项目子空间算法伪代码如下：

输入：R：二进制矩阵，m：行数

上述的算法是提出的创建子空间的算法过程，目的是通过创建的项目子空间来寻找相似用户，常用的寻找子空间的方法的时间复杂度为O(2n)，这种方法在面对实际问题时是行不通的。然而，在提出的子空间构造的方法中，每个用户u i对应的项目列表需要与其他用户(ui+1,u i+2,…,um)对应的项目列表进行m(m-1)/2次运算，并且该算法需要寻找项目的交集，其时间复杂度为O(k)，其中k代表项目列表的最大长度。综上，该过程总的时间复杂度为O(km2)，其远小于O(2n)，并且，在面对高度稀疏的数据时，k值通常很小。

2.3 消除冗余并创建邻居用户树

在所创建的项目子空间表中，存在一些在其他子空间中重复的子空间，称之为冗余子空间，消除冗余子空间可以提升推荐效率。消除冗余子空间的过程如下：（1）首先将各个子空间按照包含项目条目的数量按由多到少进行排序。（2）将被包含或重叠的冗余子空间从列表中删除。具体的处理过程如图5所示。

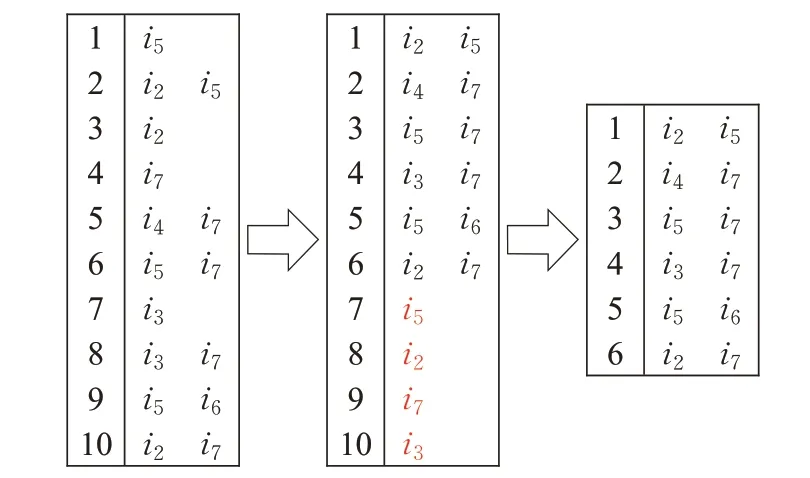
图5 消除冗余过程Fig.5 Redundancy elimination process

将子空间消除冗余后，就获得了最终的感兴趣项目的子空间，然后通过项目子空间寻找对每个子空间的用户集合，以此来构建邻居的用户树。过程图如图6所示。例如，当目标用户对项目i1、i2和i5感兴趣，则子空间(i2,i5)具有与目标用户感兴趣的项目重叠最多的项目，根据子空间用户列表可知，与目标用户最相似的用户有用户u1和u6。因此，这些用户位于目标用户邻居树的第一层，其中用户u2和u4与用户u6相似性最强，所以其位于树的第二层，以此类推，直到寻找到所有用户的相似用户，则邻居用户树构建完成。

图6 邻居用户树的构建Fig.6 Construction of neighbor user tree

2.4 邻居用户相似性计算方法

根据所提出的方法寻找到目标用户的邻居用户树，通过邻居用户树就可以知道与目标用户最相似的用户有哪些。但是，树本身就是分层的，层数的高低表示与目标用户的相似性大小，越邻近树根的位置与目标用户的相似性越强，其余次之[15]。传统协同过滤推荐算法的相似性通常采用经典的Pearson相关系数计算方法，这种计算方法对于距离目标用户最近的用户同样适用，但是与目标用户间接的邻居用户就不适用这种相似性计算方法，由于间接邻居与目标用户之间相似的项目条目的多少是不确定的，间接用户与其邻居用户之间相似性计算可以通过Pearson相关系数，所以，针对这种情况本文提出了一种改进的相似性计算方法。

本文将用户之间相似性的计算分成两部分，分别为直接邻居用户的相似性和间接邻居用户的相似性，两种类型的邻居用户之间的相似性计算公式不同。具体的相似性计算公式如下：

（1）由于受欢迎程度较大的项目是每一个用户所喜爱的，如果将其认作为是体现用户相似性的项目，明显是不正确的。其次，在原始的Pearson相似性计算公式中，只考虑用户消费的一种商品，而没有考虑用户消费同一种商品处在不同时期，例如，用户消费了物品i和j，如果消费的时间间隔越近，那么这次“同现”的权重应该越大，间隔越远权重越小，所以，要考虑惩罚时间间隔的影响。

基于上述两点，本文中结合Pearson相关系数提出了带有惩罚受欢迎程度较大项目和同一项目的时间衰减惩罚两种惩罚因子的相似性计算方法，将其作为目标用户与直接邻居用户的相似性计算公式，这样可以降低受欢迎项目以及项目的时间间隔对推荐质量的影响。计算公式为：

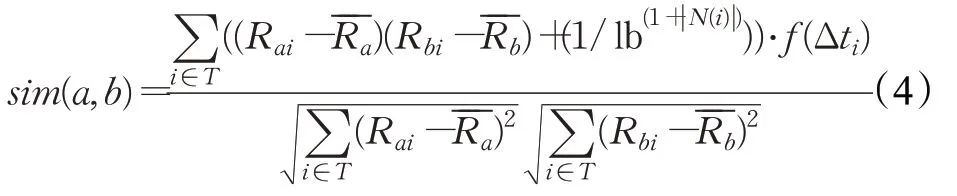
其中，sim(a,b)表示用户a和b的相似度，T表示用户a与b评分项目的交集，表示用户a和用户b的平均评分。t ai和t bi分别表示用户a和b消费物品i时的时间[17]，α为常数，用于调整时间间隔的效果。

（2）考虑到目标用户与间接邻居用户之间关系的间接性，本文提出了一种新的目标用户与间接邻居用户的相似性计算方法。计算公式为：

其中，sim(a,i)代表目标用户与间接邻居用户之间的相似度。其中用户ua和ui将通过中间邻居用户ub来进行比较。C表示由直接邻居用户u a和ub与ua和ui构成的X和Y的组合。

上述公式中的X和Y的计算公式为：

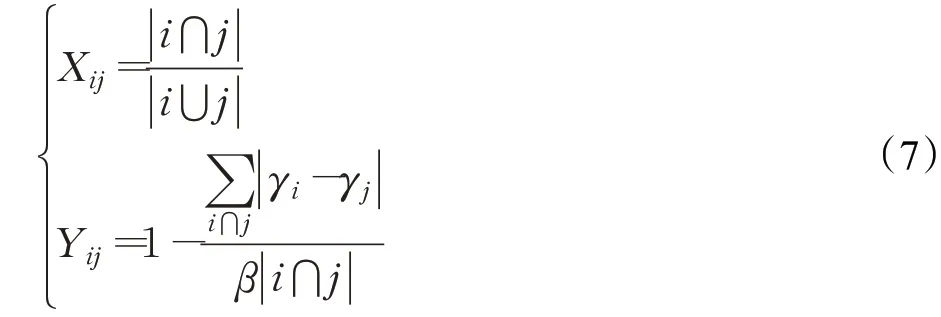
其中，Xij是传统的Jaccard系数相似性计算方法代表直接邻居用户ui和u j共同访问项目的集合表示直接邻居用户ui和u j访问项目的总和。代表用户u i和u j共同访问项目所占比率的绝对值差和[16]，β是为了增加共同访问项目的效果，是一个常数。

鉴于用户对项目的评分范围为1到5，所以本文通过用户评分将电影分为1至5五个等级，其中等级1代表烂片，等级5代表杰作。推荐的原则是推荐等级较高的电影给用户，所以本文根据Tsai所提出的54/321推荐方法，将等级4和5的电影作为推荐类别。其余等级作为非推荐类别。

3 实验分析

为了验证提出的模型的推荐性能，采用了Python作为实验的编程语言，在Windows10 64位操作系统，软件版本为Anaconda4.8.3，Python3.8.5，PyCharm2020。

3.1 实验数据

本文使用了经典的MovieLens 100K、MovieLens 1M电影评分数据集，MovieLens ML-100K数据集包含了943位用户对1 682部电影10万条评分记录，MovieLens ML-1M数据集较大，其包含6 040和用户对3 952部电影的评分记录。两个数据集包含评分值均分布在[1，5]内，均为正数，并且两个数据集的稀疏度为分别为93.7%和95.8%，能够很好地对本文提出的算法进行验证。

本文将两个电影评分数据集都分为5个交叉验证子集，其中80%的数据集作为训练集，20%数据集作为测试集，在每5个测试过程中，会有4个训练集和一个测试集，并且每次的训练子集不会重叠[18]。所以，实验结果将会取5个不同测试结果的平均值作为最终的实验结果。

3.2 实验评估指标

实验分别采用了推荐的Recall、Precision以及Accuracy作为衡量推荐性能的评价指标[19]，具体的计算公式为：

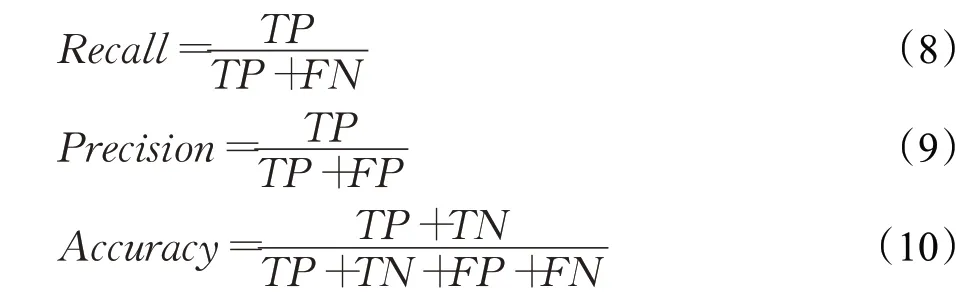
其中，TP为将正类预测为正类数，TN为将负类预测为负类数，FP为将负类预测为正类数，FN为将正类预测为负类数。

3.3 实验结果分析

为了验证所提出的推荐模型的推荐效率和质量，本文将使用不同聚类数的K-Means、不同邻居数的Pearson相关系数以及基于非负矩阵分解模型（NNMF）的推荐算法与本文所提出模型进行比较。

三种与所提出进行对比的算法，由于其三种算法在进行推荐时，都需要设置相应的参数。参数的不同将导致推荐结果的不同。首先，对于基于K-Means聚类的协同过滤推荐算法，由于该算法模型在不同聚类数下的推荐结果不同，所以，本文选取了聚类数K分别为3、5和7时，算法所展示出的推荐效果。其次，对于仅通过皮尔逊相关系数在全局内寻找相似性用户的协同过滤推荐算法，选取了其邻居用户数N分别为20、30和40时的推荐结果来进行观察对比。对于NNMF推荐模型，其不同维度得到的推荐结果也不同[20]，文中分别选取了d=3、5、7时的推荐结果作为对比。四种算法模型的具体实验结果数据如表1所示。

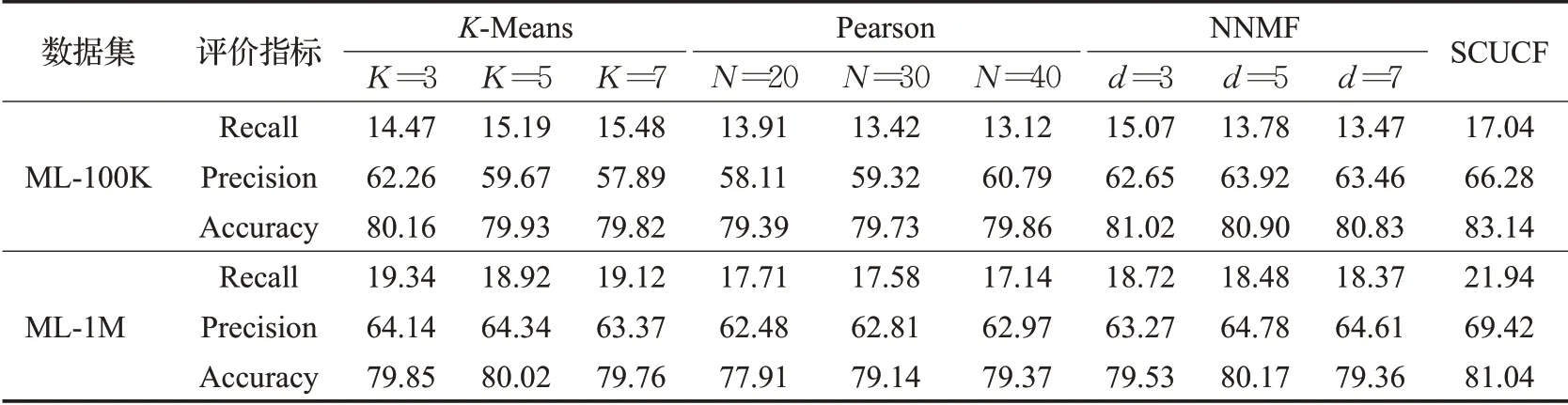
表1 四种算法的具体实验结果数据Table 1 Specific experimental results of four algorithms%

根据上述四种推荐算法模型在两种数据集上的实验结果，得到了四种算法模型的对比结果图，评估指标Recall、Precision以及Accuracy的实验结果对比结果分别如图7~9所示。

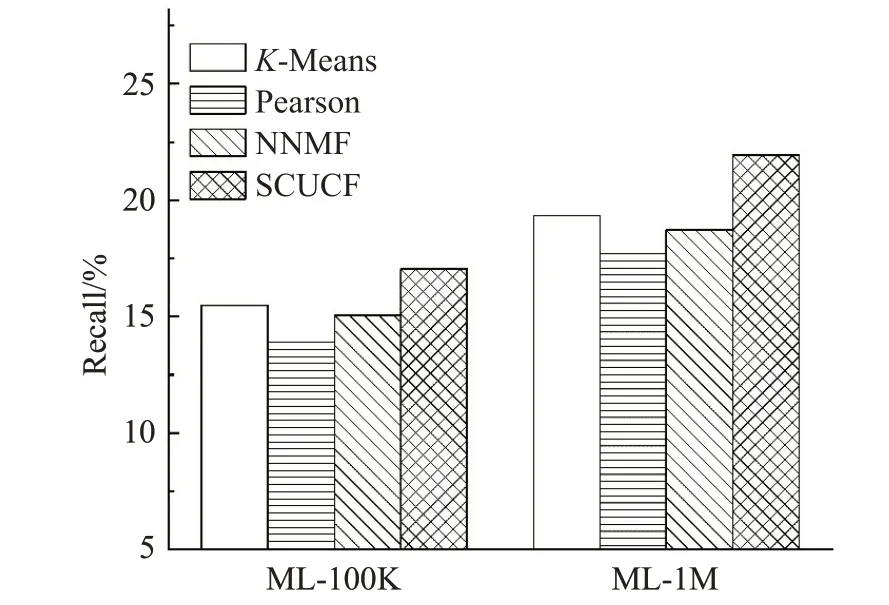
图7 四种推荐算法的召回率对比Fig.7 Recall comparison of four recommendation algorithms

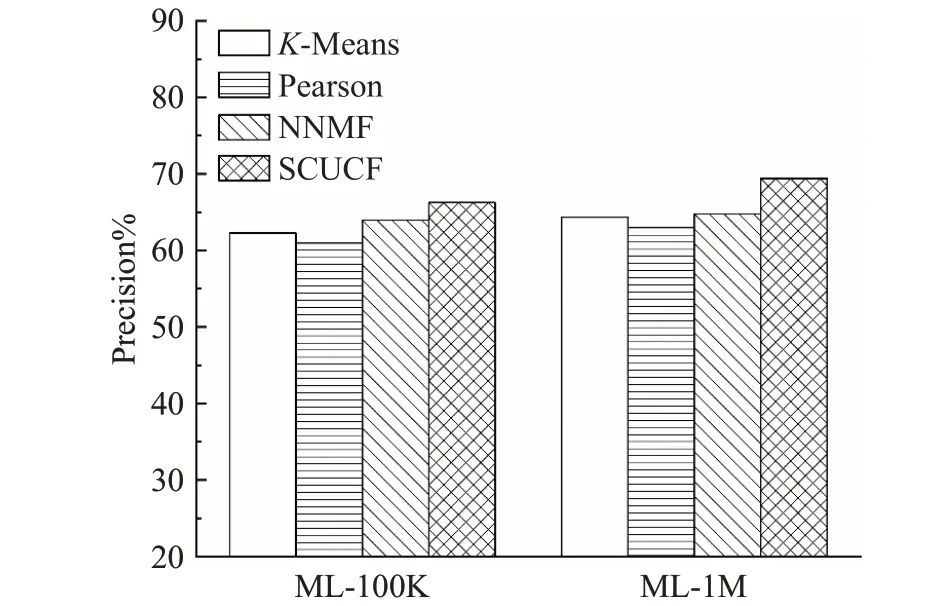
图8 四种推荐算法的精确性对比Fig.8 Precision comparison of four recommendation algorithms

图9 四种推荐算法的准确性对比Fig.9 Accuracy comparison of four recommendation algorithms

根据实验结果可以看出，提出的基于子空间聚类的推荐模型在两种数据集上的推荐性能都是优于其他几种推荐模型，在三种评价指标上，都获得了相对较好的结果，尤其是在推荐的准确性和精确性上，表现得更加明显，相比于召回率，其余两种指标更加重要，由于任何推荐算法的目的就是能够为用户提供更加准确的推荐，来更好满足用户的需求[21]。

为了验证受欢迎项目和项目时间间隔对推荐质量产生的影响，本文将引入了两个影响因素的相似性改进方法与标准方法进行了对比，并通过实验进行了验证，具体的实验结果如表2所示。

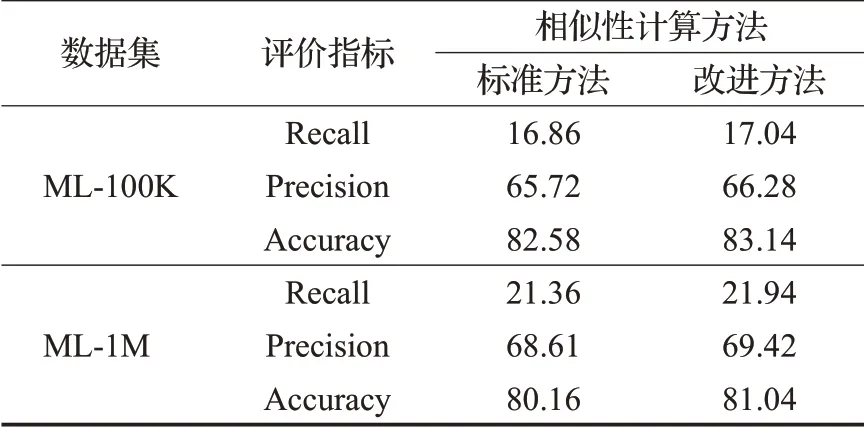
表2 两种计算方法的实验结果比较Table 2 Comparison of experimental results of two calculation methods %

根据上述的实验结果可知，改进的相似性计算方法较标准的计算方法相比[22]，其使推荐质量得到了提升。表明了项目的受欢迎程度和项目时间间隔对推荐质量产生了一定程度的影响。虽然在引入两种影响因素后仅使推荐质量得到了较小程度的提升，并因此也会伴随着实现成本的增加，但是考虑到推荐算法模型的主要目标就是为用户提供更加准确的推荐来更好地满足用户的需要。并且随着用户评分数据的增加，两种影响因素对推荐质量影响会愈发明显。所以，综上所述，本文提出的相似性计算的改进方法存在相应的合理性和必要性。

本文提出的推荐算法模型较其他几种算法模型的优势主要体现在以下几个方面：

（1）该算法较传统的协同过滤推荐算法模型相比，提高了在数据中寻找相似用户的效率，由于传统推荐算法在寻找相似用户时，直接利用相应的相似性计算方法在全局内进行计算，以寻找到目标用户的相似性用户，在时间复杂度上本文算法表现出一定的优势。

（2）与其他改进两类改进算法相比，本文所提出子空间聚类较K-Means聚类以及非负矩阵分解模型相比。该算法模型不需要确定最佳聚类数、邻居用户数等任何可调参数，不仅提高了算法的稳定性，而且也使推荐质量得到了进一步的提升。

（3）传统以及其他改进的推荐算法模型在寻找目标用户的邻居用户时，通常是完全依赖用户-项目评分信息来完成，例如，通过聚类算法寻找目标用户的邻居用户，聚类算法易受异常或噪声数据的影响而导致聚类结果出现偏差，间接导致邻居用户寻找的不准确，最终也会使推荐质量下降。然而，本文提出的寻找目标用户最佳邻居的过程是通过构建项目列表来寻找项目的子空间，通过项目子空间来绘制目标用户的邻居用户树。当存在缺失或噪声数据时，由于在寻找项目子空间的过程中，是通过寻找用户之间项目交集并消除冗余项目条目的方法来确定的，而寻找邻居用户的过程是通过寻找与用户感兴趣项目重叠最多的项目条目所对应的用户来完成的，所以即使出现一些异常数据，也不会对最终推荐结果产生很大的影响。例如，根据图6所示，当目标用户对项目i4、i5和i7感兴趣，子空间(i4,i5)和(i5,i7)具有与目标用户感兴趣项目重叠最多的项目，则用户u2、u5和u6均为目标用户的相似用户，但当用户u2和u5对项目i4的评分信息缺失时，这时目标用户的最佳邻居为用户u2和u6，但由于用户u2和u5仍然存在与目标用户感兴趣重叠的项目i7，其仍然是目标用户的第二层邻居用户，这种情况对最终的推荐结果不会产生明显的影响。并且该推荐算法模型能够在不需要确定最佳聚类数、邻居用户数等任何可调参数情况下完成推荐。所以，综上所述，该推荐算法模型与其他几种算法模型相比，具有更强的鲁棒性和稳定性。

4 结束语

鉴于传统的协同过滤推荐算法易受数据稀疏性而导致推荐质量差、效率低等问题，并且在面对高维数据时，也不能表现出很好的推荐性能。本文提出了基于子空间聚类算法的协同过滤推荐算法模型，该算法利用子空间聚类来构建目标用户的邻居用户树，以此来更快、更准确地找到目标用户的相似邻居用户，进一步缩小相似用户的搜索范围，提高推荐效率。本文针对该算法模型并结合皮尔逊相关系数提出了新的相似性度量方式。通过实验验证表明，该推荐算法模型与其他几种推荐算法模型相比，推荐性能得到了进一步的提升，并且也规避了其他算法所面临的一些问题。该推荐算法模型在一定程度上提升了推荐性能，并且也改善了一些其他寻找邻居用户算法的缺点，但冷启动问题的解决并没有在该算法中得到很好的体现，所以，下一步的研究重点是使推荐算法的数据稀疏性和冷启动问题都能够在该推荐算法模型中得到很好的改善。