基于最佳子策略记忆的强化探索策略

周瑞朋，秦 进

（贵州大学计算机科学与技术学院，贵阳 550025）

0 概述

强化学习中存在探索与利用困境，一个强化学习智能体必须尝试一些之前没有尝试过的操作，发现其中某些能有效产生奖励的动作，同时智能体也必须充分利用能有效产生奖励的经验［1］。强化学习问题中的ε-greedy 策略由于简单而被广泛使用，但在这种探索策略下智能体过度依赖于随机算子，探索完全随机，没有针对性。目前已有大量关于强化学习中有效探索的研究，如2002 年KEARNS 等［2］提出的多项式时间内的近最优强化学习，2010 年JAKSCH 等［3］提出的强化学习的近最优后悔边界。多数探索方法都依赖于随机干扰智能体的策略，如1999 年SUTTON 等［4］提出的ε-greedy，WILLIAMS［5］提出熵正则化以诱导新动作，但这些方法都限制于较小的状态动作空间或者线性函数近似，不适用于神经网络 这样的复 杂函数近 似［6］。2016 年BELLEMARE 等［7］提出基于 计数的探 索，2017 年OSTROVSKI 等［8］提出状态空间的密度建模，这些方法被尝试用来解决高维度和连续动作上的马尔科夫决策问题，但不足是它们都依赖于较为复杂的额外结构，且探索不具备针对性。2017 年PATHAK 等［9］提出的自监督好奇心模块，通过建立一个环境预测模型，对于模型预测不佳的，给予智能体一定的奖励（好奇心），这种方法在某些控制问题上有一定的效果，但是在部分控制问题上会导致智能体陷入过度探索。另一种方法是通过向算法中加入额外的关联噪声来增加自然探索，如2017 年MATTHIAS 等［10］提出使用参数空间噪声探索，2018 年FORTUNATO等［11］提出噪声网络探索。这些算法通过加入噪声干扰神经网络计算动作的Q值，从而影响智能体在当前状态下采取的动作，这些动作可能是之前没有尝试过的动作。2020 年ZHANG 等［12］提出与任务无关的探索策略，通过探索MDP，不依赖于奖励函数去收集轨迹。这些算法一定程度上提高了算法效率，但是过度依赖随机算子，干扰神经网络计算动作的Q值，其探索动作没有针对性，在探索期间，如果智能体访问到某些对于获取奖励没有帮助的状态，在这些策略下，它可能会继续深度探索这些状态及其后继状态，产生过度探索的问题。

在有限马尔科夫决策过程中，存在一个唯一的、确定的最优策略π*，其状态动作值函数Q*对于所有状态动作对都是最优的［13］，这个最优值函数满足贝尔曼最优性方程集。受此启发，笔者认为最优策略由若干局部最优策略组成。在强化学习中，一个学习任务被建模成马尔科夫决策［14］过程，那么其局部最优策略空间不可能无限大，则设计一个基于奖励排序的M 表，通过训练不断迭代最后得到一个最优策略的最优子策略空间。

本文设计基于奖励排序的M 表并改进ε-greedy算法。智能体在一定的概率下对当前样本与M 表中子策略进行匹配，若找到一个相似子策略，则选择该策略所采用的动作，通过这种方式，使智能体得到的动作具有针对性，同时提高获得的平均奖励。

1 基础理论

1.1 深度强化学习

强化学习是用于解决序贯决策的机器学习分支领域，其关键之一是智能体要学习好的行为，这意味着需要增量式地调整行为或获得新的技巧。另一个关键是强化学习通过不断试错获取经验进而学习［15］。强化学习问题通常被建模成马尔科夫决策过程，在每个时间步t，智能体所处状态为st，策略π(at|st)表示智能体在状态st下执行动作at的概率，在此概率下执行动作at，获得一个标量奖励rt，并转换到st+1，将这个过程用五元组(st，at，st-1，rt-1，done)表示，其中done 是个布尔值，用来指示一个episode 是否结束。在回合型问题中，其回报是带折扣的累积奖励，折扣因子γ∈(0，1]，是对未来预估奖励的惩罚项：

智能体的目标就是最大化每个状态的长期回报期望。通常使用值函数来预测未来回报的期望以衡量一个状态或者状态动作对的好坏。状态值函数定义为：

动作值函数定义为：

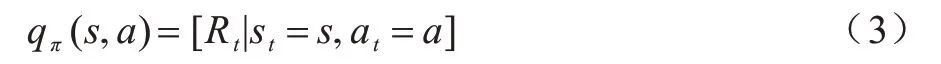
一个最优状态值被定义为：

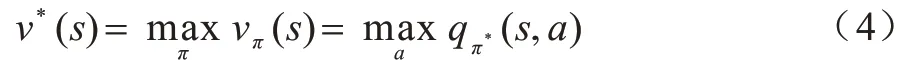
深度强化学习就是使用深度神经网络来近似强化学习中的状态值函数（或动作值函数）。深度强化学习被广泛应用于视频游戏［16］、机器人［17］、自然语言处理［18］、计算机视觉［19］等领域。2013 年，DeepMind团队将深度神经网络引入强化学习用来近似值函数。深度强化学习设置了经验缓冲，将智能体与环境进行交互产生的经验存入该缓冲，通常又称这些经验为样本。

1.2 ε-greedy 探索策略

ε-greedy 策略是强化学习中最常用的探索策略。在该策略下，智能体有ε的概率会选择一个随机动作，1-ε的概率选择当前动作Q值最大的动作，定义为：

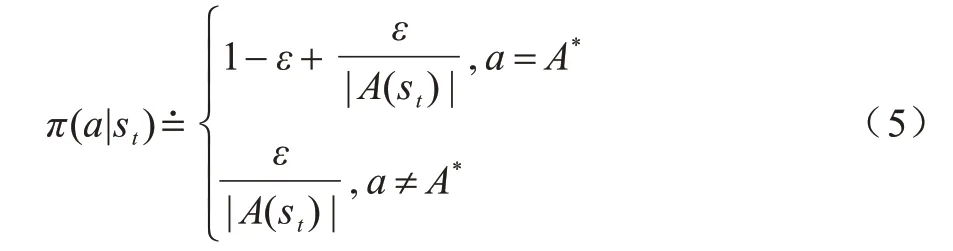
其中：A*表示最优动作；|A(st)|是当前状态st下所有可选动作的集合。

2 基于最佳子策略记忆的强化探索

定义一个强化学习问题的状态集为：

π*表示全局最优策略，由有限马尔科夫决策过程的性质可知其由若干优先的局部最优子策略组成。本文使用(st，at)表示子策略，用来近似π*，是一个向量。定义为：

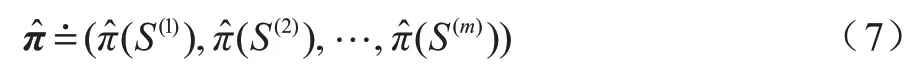
基于最佳子策略记忆的强化探索，就是将智能体目前学到的最佳子策略存入一个存储表中（记为M 表），当智能体访问M 表时，将当前状态与M 表中子策略状态进行相似度计算。若构成相似，则返回子策略中的动作。

2.1 基于奖励排序的M 表

解决过度探索，一个可行的方法是增加探索的针对性。在智能体与环境交互过程中，会产生大量的样本并将样本保存到经验缓冲中。本文将较好的经验作为子策略独立存放，在探索时，以一定的概率计算智能体当前状态与这些子策略的相似度，类似基于实例的学习，本文选择最相似的子策略中的动作并执行。通过相似计算增加智能体产生新的奖励值较高的样本的概率，这样的探索能够促进智能体获得奖励值大的样本，使探索具有针对性。如果将所有的子策略保存下来，那么空间开销和计算代价将会很大。本文使用结构性相似度算法计算子策略的相似度，将相似的子策略中奖励值最高的子策略存入M 表中，视为智能体目前学到的最佳子策略。M 表独立于经验缓冲和智能体对经验的采样过程。M 表使用二元组(st，at)来存储一个最佳子策略，并为每个子策略附加一个奖励信息rt，表示该子策略可获得的奖励，并使表中所有子策略基于奖励降序排序。M 表上的操作如图1 所示。

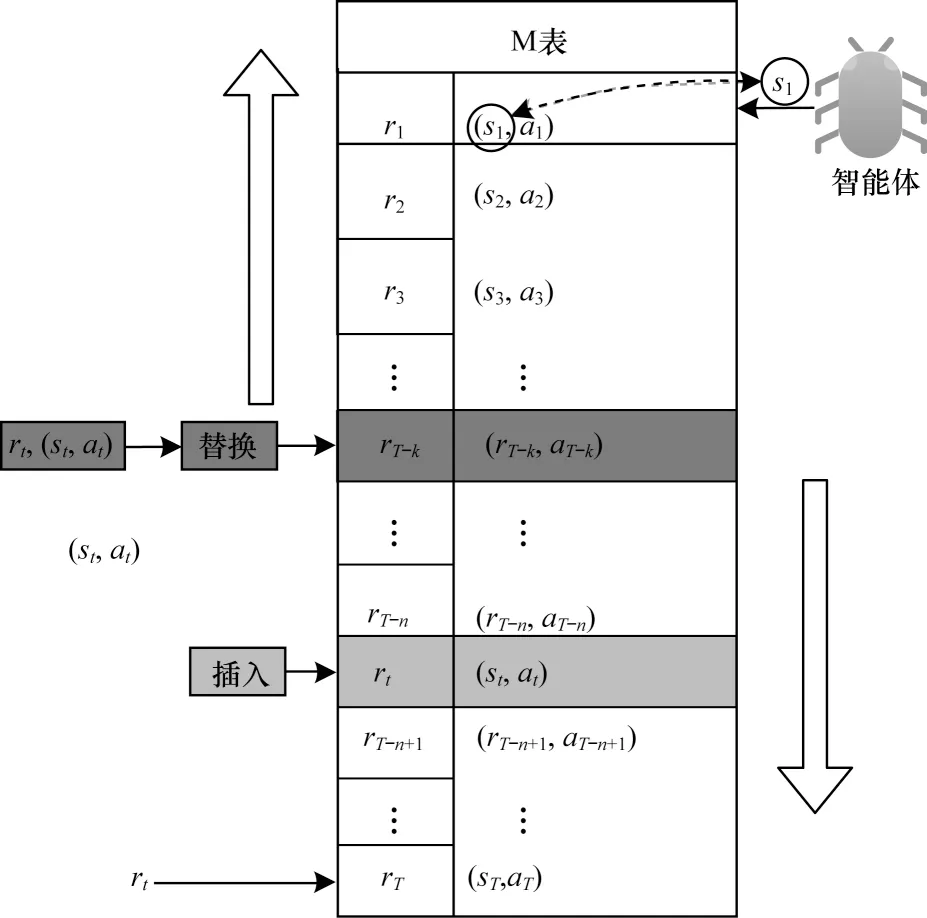
图1 M 表上的操作Fig.1 Operation on table M

如图1 的左边部分所示，智能体与环境交互产生一个新样本之后，如果样本的奖励值大于零且M 表为空，则将该样本中的子策略存入M 表。若M 表不为空，则依次判断该奖励与倒序的M 表中子策略的奖励值。若该奖励大于某个子策略(sT-k，aT-k)的奖励且小于该子策略的前继子策略(sT-k-1，aT-k-1) 的奖励，则进一步计算该样本与(sT-k，aT-k)中状态的相似度，若小于阈值θ，则认为不相似并扫描(sT-k+1，aT-k+1)前面的子策略中是否有与其相似的子策略，如果有，则跳过该策略，如果没有相似度且大于阈值θ，则认为相似，并使用样本中的子策略替换掉M 表中对应的子策略(sT-k，aT-k)，可结合图1 中3 个绿色文本框和上下子策略查看（彩色效果见《计算机工程》官网HTML 版）。若样本中的子策略(st，at)奖励值大于(sT-n+1，aT-n+1)的奖励且小于(sT-n，aT-n)的奖励，M 表中没有与其重复的子策略（若有重复，则跳过），且该子策略与(sT-n+1，aT-n+1)不相似，则将其插入(sT-n，aT-n)与(sT-n+1，aT-n+1)之间，可结合图1 中红色文本框以及上下子策略查看（彩色效果见《计算机工程》官网HTML 版）。

如果该样本的奖励大于零但不大于M 表最后一个子策略的奖励，则检查M 表前面是否有与其相似的子策略，若有，则跳过该样本，反之，则将该样本中的子策略添加到M 表的末尾。

基于最佳子策略记忆的强化探索设计智能体在探索时，将有一定的概率会通过M 表进行探索。在这种情况下，智能体会对M 表做相似查询，通过将当前状态与M 表中子策略的状态正序依次计算相似度。若与其中某个子策略的相似度大于θ，则将该子策略中的动作反馈给智能体。如图1 右半部分所示，若st与s1相似，则将该动作反馈给智能体，若不相似则继续往下找，若整个M 表都没找到，智能体将选择神经网络计算该状态下最大Q值的动作。

2.2 MEG 探索

在通常情况下，强化学习算法采用ε-greedy 探索。本文在ε-greedy 算法的基础上加以改进得到M-Epsilon-Greedy（MEG）探索。

令am为从M 中选出的最佳动作，aQ为利用神经网络选出的动作，am和aQ不同。A 为智能体所有可选动作。智能体从M 表中选出的一个动作为，sim 函数用来求智能体当前状态与M 中子策略状态的相似度，从M 表头到表尾，如果小于θ，则取对应子策略中的动作。由于前期神经网络不稳定，为了使智能体在前期保留探索能力的同时增强探索的针对性，本文将智能体利用神经网络的概率分出一部分使用M 表探索，这样智能体就既保留了探索能力，又能够有效结合目前已学最佳策略进行探索。

由此，定义MEG 探索表示为：

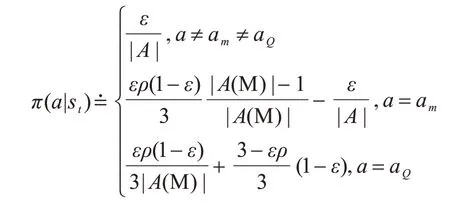
在状态st下，智能体以ε的概率选择一个随机动作a，以的概率选择对M 表进行相似查询，ρ为在M 表中找到相似子策略的概率，如果找到相似子策略，则选择子策略中的动作am，反之，则选择神经网络计算出最大Q值的动作。在的概率下选择利用神经网络计算的Q值最大的动作aQ，其中|A(M)|为M 表中所有动作的集合，|A|为智能体在该环境下的所有动作集合，探索概率设置将在下文3.1 节中详细介绍。

MEG 探索示意图如图2 所示。

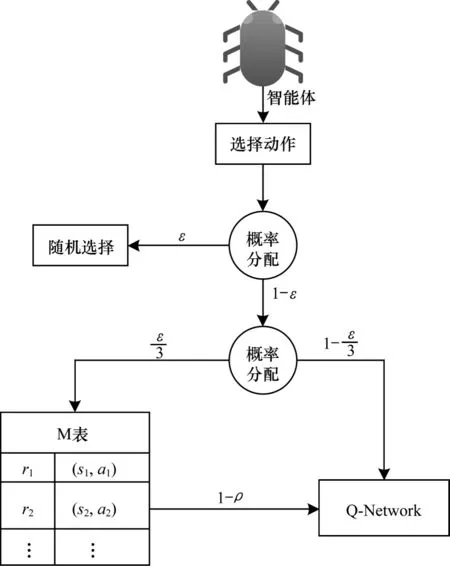
图2 MEG 探索示意图Fig.2 Schematic diagram of MEG exploration

2.3 训练

基于最佳子策略记忆的强化探索方法具有广泛适用性，为了验证其性能，本文使用FQF 算法［20］（分布强化学习的全参数分位数函数）作为实例。

将基于奖励的有序M 表和MEG 探索策略与FQF 相结合，得到M-FQF。定义经验缓冲的容量为N，每一次训练所用的数据量为一个batch_size。一个强化学习问题从开始到结束为一个episode。

为近似分位点函数网络，为分数提议网络设置H个可调分位数（τ0=0，τH=1）。分数提议网络输出对应的分位数并将这些分位数传入分位点函数网络。分位点函数网络将每个状态动作对映射到对应分位数的概率，使用1-Wasseretein 计算近似分位点函数与真实分位点函数分布之间的距离，为了最小化1-Wasserstein 误差，从固定的可调分位数τ去寻找对应的最优分位数值。分别使用RMSprop 算法和Adam 算法优化分数提议网络和分位点函数网络。将分布贝尔曼更新和分位数回归相结合训练分位点函数网络，最小化Huber 分位数回归损失（同分布强化学习的隐分位数网络IQN［21］和分位数回归的分布强化学习QR-DQN［22］，将阈值设为k）。达到训练的最低步数后，对样本采样，训练网络。最后更新分数提议网络和分位点函数网络。

3 实验与分析

3.1 实验设计

为验证改进策略的有效性，选择Playing Atari 2600游戏中的经典控制问题BankHeist、RoadRunner、Freeway、BeamRider作为实验对象，将本文改进算法与DQN系列算法以及非DQN系列的A2C算法［23］进行比较。

软件环境：Arcade Leaning Environment，CUDA10.0，Pytorch 1.5，Python3.8。硬件环境：GPU型号：Tesla P40 以及NVIDIA GeForce RTX 2080 Ti。为公平比较，对BankHeist、RoadRunner、Freeway、BeamRider 使用同状态对抗DQN的鲁棒深度强化学习［24］（SA-DQN）的参数，训练了500万个step。图中横坐标单位为250 000 step。对于Playing Atari 2600 视频游戏设置250 000 step 视频游戏帧用于探索。本文使用IQN、FQF、QR-DQN、IQNRAINBOW［25］这4 种算法作为baseline。经验回放的大小设置为1 000 000，一个训练batch_size 设置为32。折扣因子γ初始化为0.99。由于训练之初神经网络不稳定，如果利用神经网络这种不稳定性去探索显得没有针对性，因此从中分出的概率，使智能体根据M 表来探索。这一方面不影响智能体以ε的概率探索动作空间，另一方面也加强了智能体探索的针对性。使用M表探索的概率随着智能体探索概率ε线性衰减而逐渐衰减到0.01。初始化α=1e-5，θ=0.989。探索策略中的探索概率初始化为1，随着训练逐渐减少到0.01。目标网络的更新步长C为10 000。对环境Arcade Learning Environment 所反馈的奖励做归一化处理后将样本存入经验缓冲。在与A2C 算法的比较中，选择Berzerk、BeamRider这2种控制问题作为实验对象。利用openAI的开源baselines 项目中的A2C 算法作为baseline，时间步与M-FQF 同为500 万，其他参数为默认参数，epsilon为1e-5，alpha 与gamma 皆为0.99，学习率7e-4，智能体的评估间隔设置为250 000 step。

根据FQF 的实验描述，设计以下实验过程：智能体每到达一个状态s就会将状态输入基础DQN 经典网络。该网络将状态s的特征传递给分数提议网络，将输出的所有动作输入到分位点函数网络。智能体根据MEG 探索策略选择动作，以ε的概率会执行一个随机动作的概率智能体从M 表中进行相似查询选择与当前状态相似的子策略中的动作。以的概率选择分数提议网络预测的最大状态动作值执行动作a，环境反馈奖励和下一个状态后，将产生的样本存入经验回放，再进行采样、训练。

3.2 实验结果与分析

深度强化学习中算法效果主要由奖励值决定。网络在设定的迭代次数结束后，平均奖励越大说明该算法的性能越好。M-FQF 在实验环境Arcade Learning Environment 中4 种控制问题上的实验结果如图3～图7 所示（彩色效果见《计算机工程》官网HTML 版）。

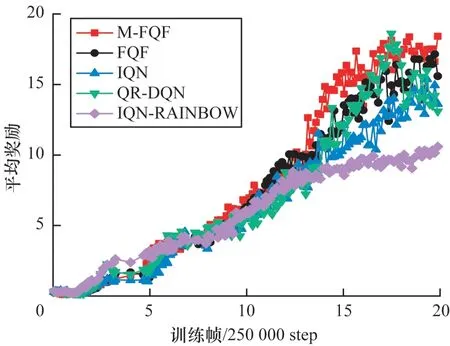
图3 5 种算法在BankHeist 上的平均奖励Fig.3 Average reward of five algorithms on BankHeist

通过实验对比发现，结合了基于奖励有序的M表探索策略 的FQF 算法（M-FQF）相较于FQF、IQN、QR-DQN、IQN-RAINBOW 算法，在多数控制问题上取得了更高的平均奖励且具有更好的稳定性。

图3 中约1.25×2 500 000 step 处5 种算法 突然性能变化较大，这可能是刚好更新了目标网络，这时候更能体现算法本身的稳健性。IQN-RAINBOW 在经过这个点后就趋于平稳，获得的平均奖励是5 种算法中最低的。M-FQF 和FQF 趋势有点相似，但是从图中可以看出M-FQF 明显要优于FQF 以及其他3 种算法。图4 中游戏开局5 种算法的起点都不在原点，这是因为Freeway 游戏开局距离游戏得分处有一小段距离。约在2.5×250 000 step 到4×250 000 step 之间应该是智能体学习的一个关键阶段。因为在这里5 种算法出现了不同程度的波峰或者波谷，只有QR-DQN 形成了一个波谷。相比其他4 种算法，QR-DQN 似乎受影响更大。可以看出这个问题上最优的算法是IQN-RAINBOW，其次是M-FQF。此外，5 种算法在Freeway 上都有较好的收敛性。

图4 5 种算法在Freeway 上的平均奖励Fig.4 Average reward of five algorithms on Freeway

在RoadRunner 问题上，从图5 看出M-FQF 和IQN-RAINBOW 都有较好的收敛性。IQN-RAINBOW收敛更快，在初期其平均奖励更高，但是其收敛的平均奖励明显低于M-FQF。M-FQF在该问题上表现最好。从图6 可以看出，M-FQF 在该问题上收敛较为缓慢，但是最后获得了较高的平均奖励，说明其学习到了一个较好的策略。而IQN-RAINBOW 依然收敛最快，但是收敛的平均奖励并不高且稳定性不好，出现了很多明显的波峰和波谷。M-FQF 则相对稳健，整个训练过程没有出现明显的波峰和波谷。Berzerk 问题的训练情况如图7 所示，M-FQF 和IQN-RAINBOW 收敛都很快，初期IQN-RAINBOW就获得了最高平均奖励，比M-FQF还稍高一些。但在5×250 000 step 后IQN-RAINBOW就趋于收敛了，与其同时，其他3 种算法也都趋于收敛，而M-FQF 平均奖励还在不断上升，最后获得了最高的平均奖励。可以看出，在Berzerk 问题上，M-FQF 算法性能最优，QR-DQN 性能最差。

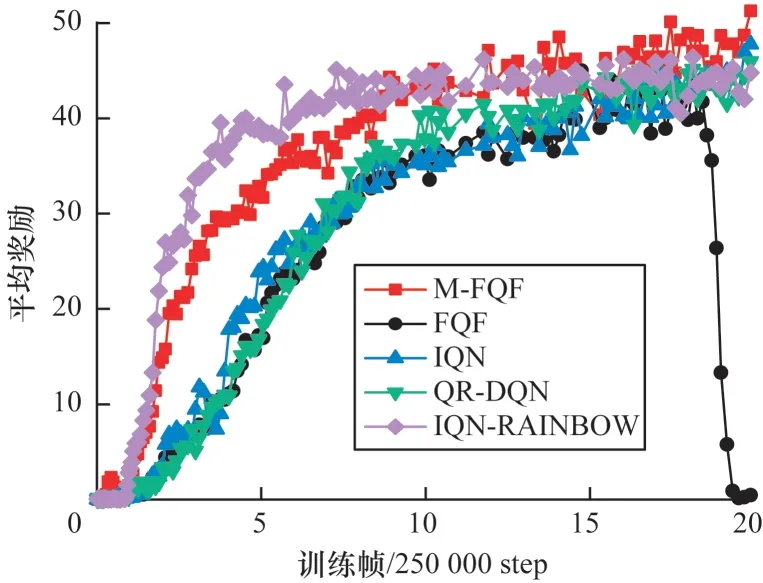
图5 5 种算法在RoadRunner 上的平均奖励Fig.5 Average reward of five algorithms on RoadRunner

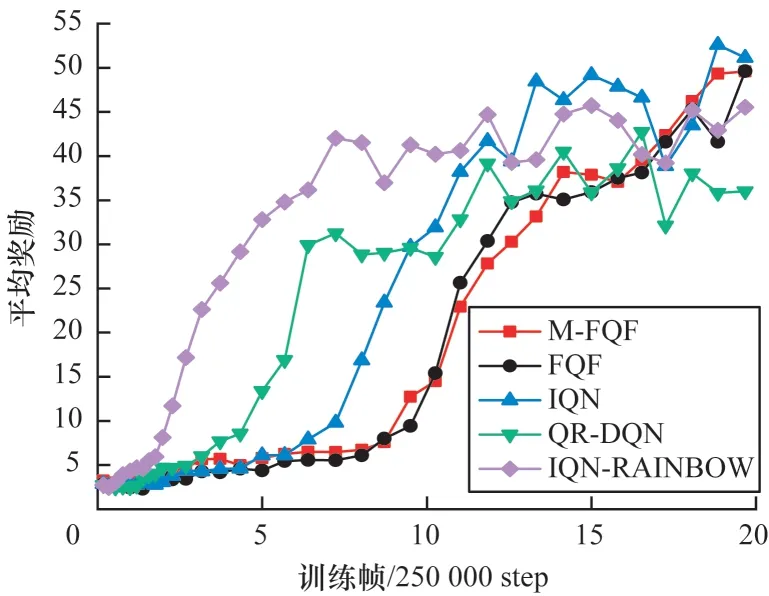
图6 5 种算法在BeamRider 上的平均奖励Fig.6 Average reward of five algorithms on BeamRider

图7 5 种算法在Berzerk 上的平均奖励Fig.7 Average reward of five algorithms on Berzerk

将M-FQF 与非DQN 系列算法的A2C 进行比较，如图8 和图9 所示。

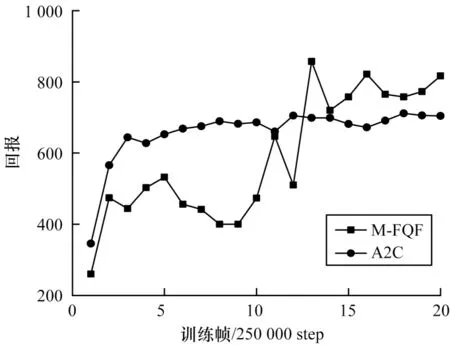
图8 M-FQF 和A2C 算法在Berzerk 上的回报Fig.8 Return of M-FQF and A2C algorithms on Berzerk

图9 M-FQF 和A2C 算法算法在BeamRider 上的回报Fig.9 Return of M-FQF and A2C algorithms on BeamRider

从图8 可以看出，Berzerk 问题上A2C 算法收敛很快，在2.5×250 000 step 左右已经获得较高的回报。反观M-FQF 算法在1.25×2 500 000 step 之前尚未表现出收敛，1.25×2 500 000 step 以后M-FQF 算法反超A2C 算法，获得了相对高的回报。图9 中A2C 算法趋于平稳，而M-FQF 算法获得了相对高的回报。可以看出A2C算法相对稳定，而M-FQF算法相对有些波动，不够稳定。

除了与以上算法进行比较，本文对比了加入MEG探索和加入噪声网络以及优先经验回放在Bankheist和Roadrunner 问题上的性能，如图10 和图11 所示（彩色效果见《计算机工程》官网HTML 版），可以看出，加入了MEG 探索的FQF 算法性能明显提高。

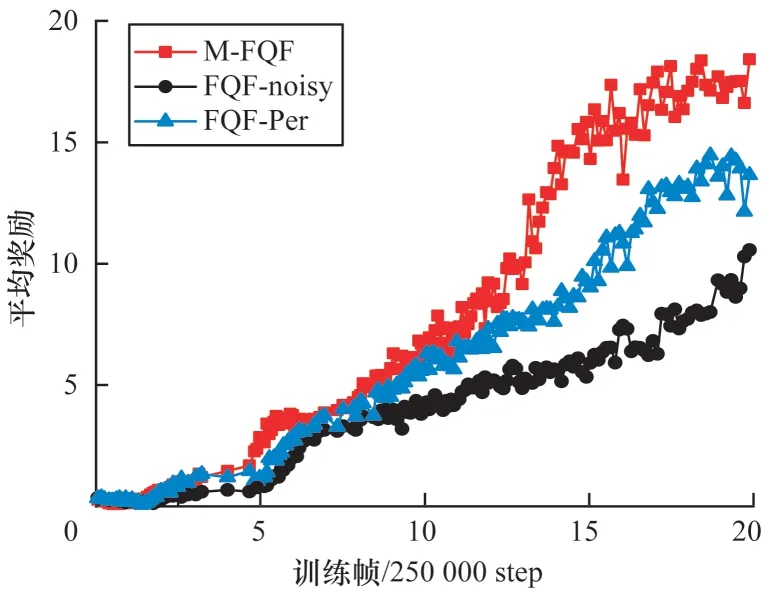
图10 FQF 算法在BankHeist 上的平均奖励Fig.10 Average reward of FQF algorithms on BankHeist

图11 FQF 算法在RoadRunner 上的平均奖励Fig.11 Average reward of FQF algorithms on RoadRunner

为测试MEG 探索是否对收敛结束时的参数值有依赖，在BankHeist 环境下做了4 个实验，设置算法收敛过程中使用随机探索和MEG探索的概率之和为0.01。用e表示随机探索的概率，m表示使用MEG 探索的概率。M-FQF 不同探索参数的平均奖励如图12 所示（彩色效果见《计算机工程》官网HTML 版）。

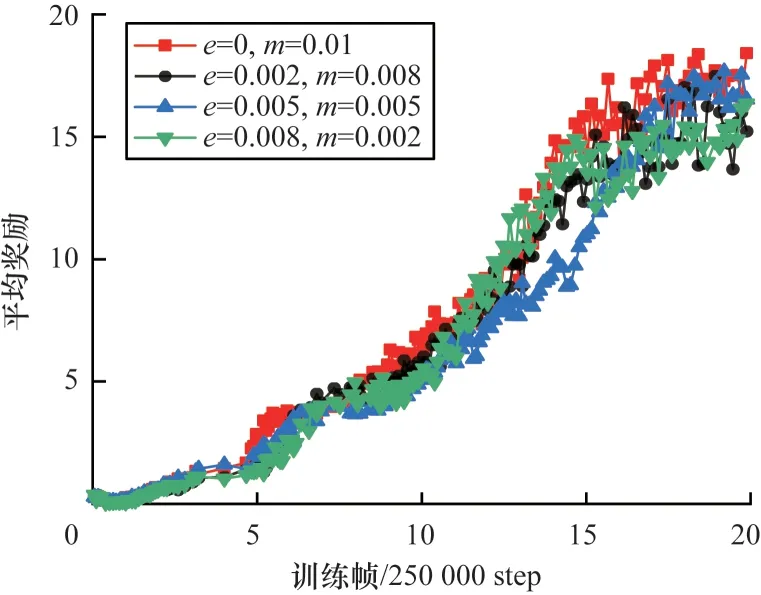
图12 M-FQF 算法在BankHeist 上的平均奖励Fig.12 Average reward of M-FQF algorithm on BankHeist

可以看出，随着智能体使用MEG 探索的概率从0.01 下降到0.002，智能体所获得的平均奖励也在不断减少，说明M-FQF 算法对于收敛过程中MEG 探索的概率参数设置有所依赖，使用MEG 探索的概率越大，算法性能越好。

4 结束语

本文设计一个基于奖励排序的M 表，进而提出基于M 表的MEG 探索策略，并都加入到FQF 算法中，以提高算法的探索效率，缓解过度探索的问题。实验结果表明，该策略在Playing Atari 2600 游戏中取得了较高的平均奖励。但MEG 探索依然存在不足，如在部分游戏中收敛速度缓慢。下一步将针对此问题，通过调整探索方法进一步优化MEG 探索效果，如将M 表中实际存在的最佳子策略个数和有效访问次数考虑在利用M 表进行探索的概率计算过程中，或对M 表中的最佳子策略进行路径规划，通过逻辑处理导出新的最佳子策略或启发策略。