基于有限单元法的路灯杆结构优化选型设计*

王芳妮，别 俊，胡 岩，文海龙，郑玉卿※，吴建华

（1.湖州师范学院工学院，浙江湖州 313000；2.湖北三环智能科技有限公司，武汉 430074）

0 引言

根据国家统计局数据显示，我国道路路灯平均每8年更换一次，且每一次更换和新增数都在大幅度地增长。随着城市化进程不断加快，中国信息网《我国城市照明行业概况及发展趋势分析》报告中显示路灯在2015年新增了174万余座，更换路灯个数为111万余座，总计个数286 万余座[1]。通过调查路灯生产、安装和施工方面的国家政策，如《CJJ89-2016-城市道路照明工程施工及验收规程》[2]、《GB 7000.5-2016 道路与街路照明灯具安全要求》[3]、《CJJ45-2015 城市道路照明设计标准》[4]、《全面质量管理办法路灯质量标准(试行)》[5]等，政策上主要对电杆掩埋深度、焊接要求、倾斜程度与配电等方面做出要求，但目前我国对路灯杆结构参数并无明确规定，仅个别路灯杆生产厂家有标准的生产规格，要求抗12级风载[6]。另外，对路灯杆参数的优化研究少之又少，仅仅有一部分关于智慧路灯系统[7]及路灯智能控制系统[8-9]的研究。

本文研究的目的是基于有限单元法[11]和理论强度校核，在满足强度使用条件下，通过合理的路灯杆结构参数优化设计计算[10]，实现路灯杆整体降重，避免城市照明工程建设过程中钢材过度使用，从而降低城市照明建设成本。首先，拟选取受12级均布风载荷的空心圆柱悬臂梁作为基础模型进行理论强度计算，并采用Altair Hyperworks 13.0 中的Optistruct 模块进行有限元建模和仿真计算，提取仿真结果中的路灯杆顶端挠度值与根部危险截面等效应力[12]，与理论计算结果进行对比，两者偏差范围控制在10%之内，构建出一个能准确反映路灯杆真实受载情况的有限元基础仿真模型。其次，对某市范围内的路灯杆进行三维结构建模，并进行多轮次的优化仿真计算，得出合理的路灯杆壁厚和最高降重比例，为路灯杆的结构设计提供新的思路。

1 路灯杆理论强度设计

1.1 路灯杆理论风载模型

经查阅，一般路灯杆材质为Q235 钢，空心薄壁圆管，其机械性能如表1 所示，一般路灯杆杆长10 m，杆梢直径170 mm，杆根直径170 mm，平均壁厚t=4 mm，12 级风压载荷，在本次仿真中将路灯杆简化为受风压的圆柱悬臂梁，通过对悬臂梁的理论计算得出路灯杆能抵抗12级风压载荷时的最小壁厚值。该悬臂梁主要受均布载荷q作用。力的作用将在路灯杆不同截面处产生不同弯矩和剪力，根据弯矩图，经过理论计算可得危险截面应力、挠度大小，以及达到许用应力条件下的最小灯杆壁厚。

表1 Q235机械性能

路灯杆理论受载模型中风力均布载荷分布如图1 所示，参照材料力学中悬臂梁的均布载荷计算公式，根据下式进行计算[13]：

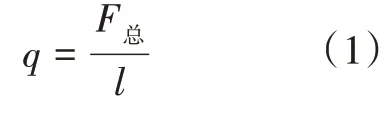
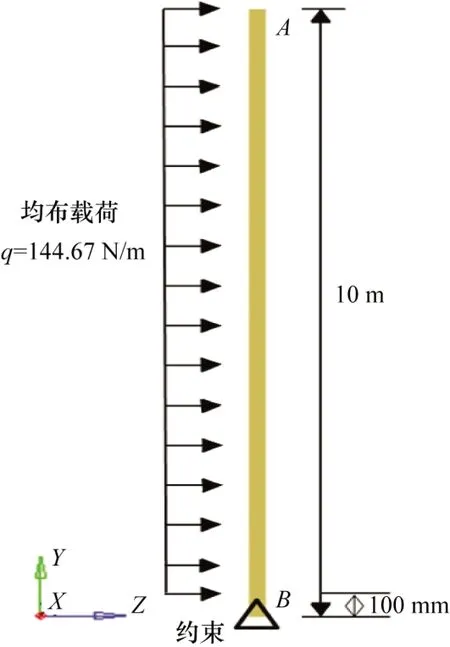
图1 路灯杆理论风载模型

式 中：F总=wp×S杆，S杆为路灯杆纵截面面积，基础模型路灯杆纵截面面积为1.7 m2。

在进行风压计算时，为了保证后续结构仿真计算的准确性，参考了大量风压对不同建筑物产生影响的参考文献，如冯帅[16]研究了风场对物体位移的影响，应用峰值分段平均法估算建筑结构表面的极值风压系数并进行不同时距修正进而进行风压估计，胡柱[17]、夏哈等[18]研究了风力对底端固定实体受风压造成的应力变化等，最后根据下式进行风压计算：

式中：wp为风压，取851 N/m2；v为风速，对于12 级大风，取风速上限值为36.9 m/s。

因此F总= 1446.7 N，q=F总/l=144.67 N/m。

1.2 路灯杆弯矩图

路灯杆弯矩计算公式为[13]：

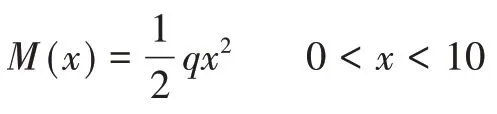
路灯杆弯矩图如图2所示。

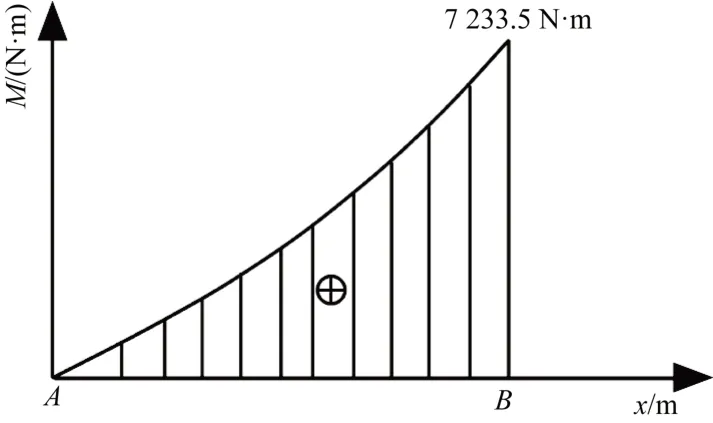
图2 路灯杆理论模型弯矩

1.3 危险截面应力计算

由弯矩图可以看出，在路灯杆根部承受了最大剪力和最大弯矩，最大弯矩为7 233.5 N·m，因此最大弯矩面应该是路灯杆根部的截面。

危险截面应力根据下式进行计算[13]：

式中：σ为危险截面应力；[σ]为许用应力；Mmax为最大弯 矩，Mmax= 7 233.5 N·m；Wz为抗弯截面系数，为路灯杆截面内径且d=170 mm，D为路灯杆截面外径且D=170 mm。

则σ= 85.5 MPa，可见路灯杆根部最大等效应力85.5 MPa。

1.4 挠度计算

路灯杆顶端最大挠度根据下式进行计算[13]：

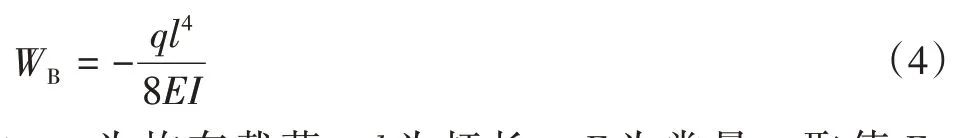
式中：q为均布载荷；l为杆长；E为常量，取值E=210 000 MPa；I为截面惯性矩，将对应的数据代入后可得：

WB= 0.119 m = 119 mm。

可见路灯杆顶端的最大扰度为119 mm。杆体产生最大挠度的主要原因是该杆体高度远高于其他实验杆体，风压一定的情况下，受力面积增加，伴随着整个杆体承受的压力更大，因此产生的挠度将会远高于其他高度较低的杆体。

1.5 壁厚计算

计算基础模型在许用应力164 MPa 的条件下的最小壁厚。

由式（3）变形得：

将Mmax、d等数据代入式（5）可得：D=165 mm，tmin=2.5 mm。计算得到在12 级风压下可承受的最小壁厚比查阅到的平均壁厚t=4 mm 小了37.5%，这表明目前路灯杆存在较大的优化空间，可以通过降低一定的壁厚来减少钢材的耗费。

1.6 有限元仿真计算

在针对理论强度计算的基础几何模型进行仿真分析时，为了保证后续结构仿真计算的准确性，参考了大量薄壁管应力仿真分析的参考文献，如姜康[15]关于侧风对大跨度桥梁轿车行车安全影响的仿真分析是基于动力学参数建立仿真模拟，通过仿真实验对整车的动力性，平稳性进行研究，实现了多平台联合以模拟复杂工况和数据的后处理。彭立国[14]使用有限元软件ANSYS 对管线进行强度计算，并对稳定性与局部应力进行分析，再应用压力管道标准规范和压力容器标准规范对管道系统的整体和局部分析结果进行双重校核等。通过借鉴前人对仿真方面的分析方法，基于Hyperworks 建立了对应的有限元数值仿真模型，采用三角形与四边形混合的2D 网格，厚度t=4 mm，赋予材料一定的模型属性（表1）。将路灯杆根部100 mm 段进行6 个方向的约束，整个模型网格节点共计5 950 个，载荷为单个节点赋予0.24 N 共计1 446.7 N，然后沿Z轴给予正向载荷，进行仿真分析。

仿真结果显示最大挠度为117.4 mm，危险截面等效应力σ=87 MPa，如图3 所示。两者分别与理论挠度计算值和危险截面应力值对比，两项的误差均小于5%。由此可见，有限元仿真计算模型具有很高的仿真精度和预测性能[11]。

2 路灯杆仿真优化设计

基于上述理论校核的有限元仿真模型进行对路灯杆结构参数优化分析，优化流程如图4所示。

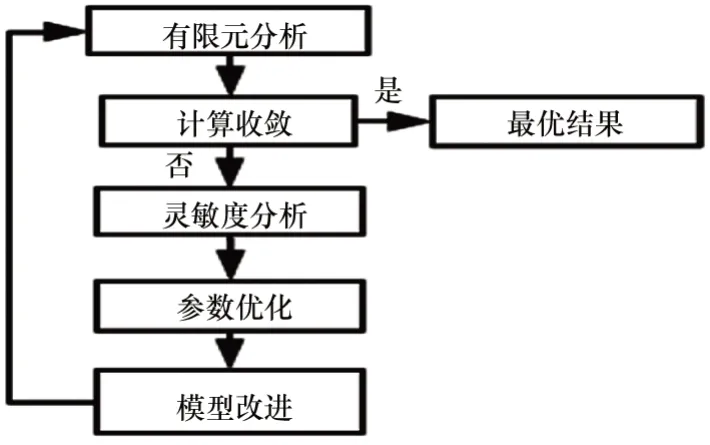
图4 优化计算流程

其中设置优化目标为路灯杆体积最小，优化参数选取路灯杆壁厚t，优化约束为路灯杆最大应力需小于材料标称的屈服强度235 MPa。如图5所示为不同路灯杆壁厚情况下优化仿真结果。集中所有数据表现出一个现象，即无论顶端挠度多大，路灯杆均未产生局部的严重变形或者撕裂，从计算结果中也可以判断出在最小杆壁厚度为2 mm 的情况下，路灯杆即可承受12 级风力产生的风压，并保持稳定性，且危险截面材料的许用应力范围小于Q235材料屈服应力，整体减重效果可达40%，可以节约钢材使用和制造成本。

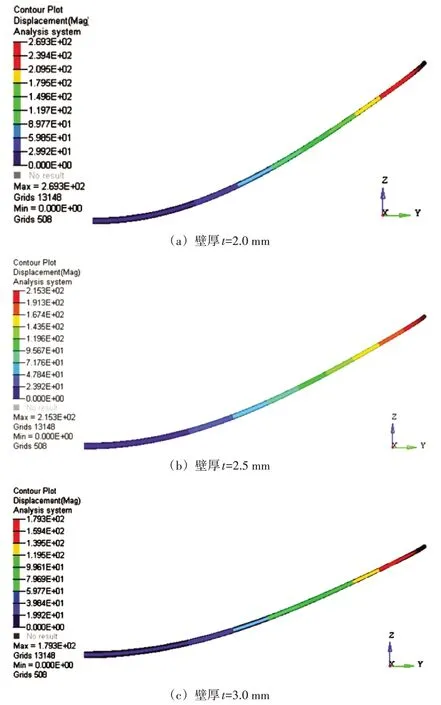
图5 不同壁厚路灯杆优化仿真结果对比

3 结束语

基于Hyperworks 创建有限元仿真模型能够预测路灯杆在极限风载工况下的结构响应，且仿真精度误差在5%以内。基于准确的有限元模型进行结构参数优化迭代可较好地预测不同规格型号的路灯杆抗风性能，从而避免了大量的实物验证，节约结构设计时间和试验测试成本。

路灯杆优化仿真结果对比可知，当路灯杆钢管壁厚为2.0 mm 时，路灯杆不仅强度方面（顶端挠度和根部弯曲应力水平）能满足12级大风载荷使用工况，且在整体重量上可减重40%，这为降低现有路灯杆的钢材使用量提供了不少设计空间。本文的研究成果将有助于城市道路路灯杆设计的优化选型，有助于降低城市照明工程的建设成本。