弧形水工闸门加固结构优化设计方案分析研究

缪融融，唐 演

（江苏省淮沭新河管理处，江苏 淮安 223000）

1 引言

水工结构运营过程中，其安全稳定性受运营年限[1]、材料安全允许应力值[2]等影响，研究结构安全可靠性势必需要考虑设计因素。为此，基于水工设计的优化分析，探讨工程安全的最优化结果，对工程设计、建设成本控制等均有重要意义。针对工程设计最优化问题，邱海娟[3]、沈卫[4]基于水工模型试验理论，设计开展泄洪洞、溢洪道等水工设施的模型试验，分析不同设计方案下模型试验结果差异性，进而获得工程建设的最优设计方案。模型试验方法虽可靠性较大，但试验成本及耗时周期不利于设计进度要求，因而一些学者利用Abaqus[5]、ANSYS[6]等数值仿真平台，通过分析有限元计算模型在不同设计方案下静力场或渗流场特征，可较高效获得不同方案的利弊性，进而为工程建设提供重要计算依据。文中根据某节制闸弧形钢闸门的加固问题，设计探讨放大增强体截面半径尺寸参数最优化，为工程除险加固提供重要参考。

2 工程设计概况

2.1 工程概况

某节制闸作为区域内重要水利控制枢纽，其运营安全稳定性乃是日常监管、维护的重中之重，承担着地区农田灌溉、防洪排涝、蓄水调度的水利作用，年可灌溉农田270万亩，所建设的输水渠道全长为80 km。节制闸年最大泄流量超过350万m3，闸顶高程与泄流水面线距离为1.2 m左右。为减少节制闸前水力作用影响整体水闸枢纽功能，工程管理部门讨论对节制闸的弧形闸门进行加固，既可增强闸体所在区域的水力控制性能，也可提升节制闸对下游水利控制效率。设计部门计划采用增设放大增强体的措施，提升闸门结构整体抗倾覆性能，而放大体设定在弧形闸门的墩体与闸室边侧相交部位，如图1所示。

图1 增强放大体示意图

2.2 工程仿真

为确保工程设计方案优化分析结果的可靠性，采用COMSOL有限元仿真平台建立节制闸弧型钢闸门与增强体的计算模型[7]，如图2所示。该模型主要采用四边体微单元网格，经划分后获得微单元体86 282个，节点数62 566个。该模型中外荷载包括有结构自重、静水压力及泥沙悬浮沉降作用等，模型计算范围为节制闸上、下游各50 m，闸室底部土体影响范围为20 m。为方便计算分析，文中设定计算模型的X、Y、Z正向分别为顺水流下游、闸体竖直向上及闸门右岸向。基于不同放大增强体设计方案的对比，分析各设计方案中增强体尺寸半径参数对结构静力稳定性影响，进而获得最优设计方案。

图2 节制闸门整体模型

3 闸门结构应力特征

墩体放大增强体位移节制闸两侧，设定左、右侧增强体截面尺寸半径参数均为一致，设定参数分别为0.6 m（A方案）、0.8 m（B方案）、1.0 m（C方案）、1.2 m（D方案）、1.4 m（E方案）、1.6 m（F方案），其他设计参数一致，计算增大体的截面参数对节制闸水工闸门应力、位移影响。另一方面，在计算模型中以关键部位的静力参数为分析重点，各关键部位如图3所示。

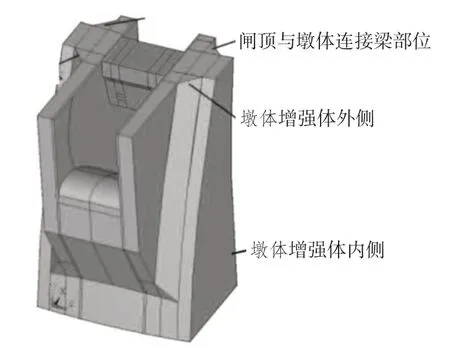
图3 节制闸关键部位示意图

3.1 拉应力特征

根据墩体放大增强体的设计方案对比，获得节制闸拉应力变化特征，如图4。依据图4中应力变化趋势可知，3个关键部位最大拉应力随增强体半径参数均为递减变化，但各部位拉应力量值均有差异，以闸墩内侧面部位上的拉应力为节制闸上最高。从整体来看，各设计方案中闸墩内侧面部位最大拉应力分布为1.45~4.7 MPa，而墩体外侧面、连接梁部位最大拉应力与前者差幅分别为21.5%~32.7%、54.4%~82%，即3个部位中连接梁部位处拉应力最低，且各设计方案中连接梁处拉应力均未超过2.2 MPa，而墩体内侧面部位最大拉应力在半径0.6 m方案中甚至可达3.45 MPa，为工程安全设计考虑，设计配筋之时应重点加密墩体内侧面，增强其刚度。

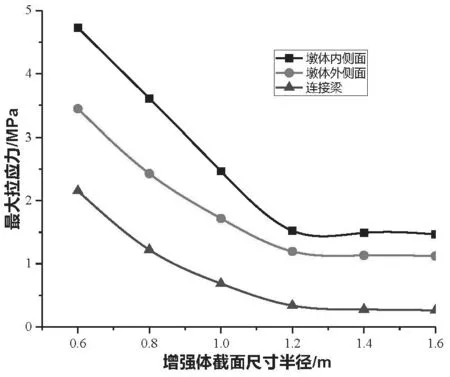
图4 关键部位最大拉应力与增强体半径参数关系

对比放大增强体对闸体关键部位拉应力影响可知，各部位最大拉应力随墩体半径参数变化的降幅具有转变节点，3个部位均在增强体半径1.2 m处拉应力降幅放缓。在增强体半径0.6~1.2 m区间内，半径参数每增大0.2 m，墩体外侧面最大拉应力随之减少29.7%；而增强体半径参数超过1.2 m后，墩体外侧面最大拉应力平均降幅仅为3.1%，即增强体截面尺寸对墩体外侧面拉应力抑制作用减弱，特别是在半径尺寸参数超过1.2 m后，墩体外侧面上最大拉应力均低于1.5 MPa，满足结构材料安全允许值。同样，在增强体半径0.6~1.2 m区间内，墩体内侧面、连接梁部位最大拉应力分别具有平均降幅31.2%、45.9%；而在增强体半径1.2~1.6 m内，两部位的降幅又为1.9%、11.4%，即连接梁部位受增强体截面尺寸参数影响更为敏感，因此，控制墩体半径参数在适宜区间乃是更为有利，从文中拉应力计算结果考虑，放大增强体半径参数1.2 m时乃是最优。

3.2 压应力特征

同理，可获得3个关键部位上最大压应力随增强体半径参数变化关系，如图5。依据图5中压应力表现可知，3个部位中压应力最大为连接梁，在6个设计方案中连接梁压应力分布在8.66~15.45 MPa，而墩体内侧面、外侧面最大压应力较前者的差幅分布为25.7%~43%、13.3%~24.2%；从结构设计考虑，连接梁部位乃是重要耦合节点，其受静水压力、结构自重等影响，因而压应力乃是闸体最大。从3个部位与增强体半径参数变化关系可知，连接梁部位最大压应力随之为先增后减变化，以增强体半径1.2 m方案为压应力最大。在增强体半径参数0.6~1.2 m区间内，连接梁最大压应力随半径参数为递增，半径每增大0.2 m，连接梁最大压应力增长21.5%，该区间内连接梁所受预压效果最为显著，有利于结构抗倾覆[8]；而在半径1.2~1.6 m区间内，平均降幅为9.5%，分析表明连接梁部位压应力效果最好为半径1.2 m。墩体内、外侧面最大压应力随半径参数均为递增态势，各设计方案中墩体内、外侧面最大压应力随增强体半径参数的平均增幅分别为11.9%、10.3%，但在半径0.6~1.2 m区间，内、外侧面压应力的平均增幅可达19.6%、17%，超过1.2 m后最大压应力变幅较小，分别稳定在9.33 MPa、12.05 MPa。综合分析认为，当放大增强体的半径为1.2 m时，不仅连接梁部位抗倾覆效果最佳，且墩体内、外侧面的压应力处于最经济，因而增强体半径1.2 m时结构体系应力效果最优。

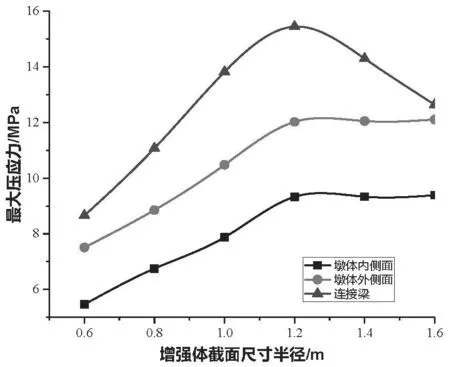
图5 关键部位最大压应力与增强体半径参数关系

4 闸门结构位移特征

根据对增强放大体设计方案位移计算，获得典型方案下闸墩内、外侧面位移分布特征，图6、图7为放大体半径0.6 m、1.2 m时墩体Z向位移特征。

从图6中可看出，在放大体半径0.6 m设计方案中墩体内侧面负向位移最大为2.94 mm，该部分负向位移乃是由于墩体内侧面部位上的拉应力产生，负向位移集中区间位于2.27~2.94 mm。该设计方案中墩体内侧面指向闸体右岸方向最大位移为3.13 mm，分布于内侧面与外侧面转角处，分布面积较小，稳定在2.45~3.31 mm，表明增大体的半径参数增大，有助于控制结构体系位移的扩展延伸。外侧面位移分布与内侧面具有对称特性，其正、负向最大位移与内侧面为“镜面”特性。当放大体半径增大至1.2 m后，墩体内侧面上最大位移逐步转移至墩顶，该部位处抗拉、抗倾覆效果最佳，而Z向最大负位移位于该处，有利于控制结构材料裂纹的扩展，且位移分布为1.79~2.49 mm，降幅达24.8%~45.9%。该设计方案下，结构的位移分布显著处于较安全合理。综合对比，可知放大增强体半径1.2 m时为最优设计方案。

图6 放大体半径0.6 m时墩体Z向位移特征

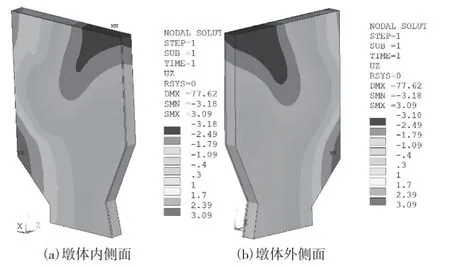
图7 放大体半径1.2 m时墩体Z向位移特征

5 结论

（1）3个部位中拉应力最大为墩体内侧面，墩体外侧面、连接梁部位最大拉应力与之差幅分别为21.5%~32.7%、54.4%~82%；各部位最大拉应力随墩体半径参数为递减，墩体内、外侧面及连接梁部位最大拉应力的平均降幅分别为31.2%、29.7%、45.9%，而半径1.2~1.6 m降幅分别为1.9%、3.1%、11.4%。

（2）3个部位中压应力最大为连接梁部位，连接梁部位最大压应力在半径1.2 m方案为压应力最大。墩体内、外侧面最大压应力随半径参数均为递增，但在半径1.2 m后增幅较小，分别稳定在9.33 MPa、12.05 MPa。

（3）墩体内、外侧面正、负Z向位移分布具有“镜面”特性，放大体半径增大至1.2 m后，Z向负位移向墩顶集中。

（4）综合应力、位移特征，节制闸的放大增强体半径1.2 m时为最优设计方案。