圆极化解耦手性辅助超表面

王禹翔，袁乐眙，李金星，吴 群，张 狂

(哈尔滨工业大学 电子与信息工程学院，黑龙江 哈尔滨 150001)

0 引言

超表面作为一种二维平面化的超材料结构，可以通过改变局部亚结构来灵活地对电磁波幅度[1]、相位[2]和极化[3]进行调控。由于超表面低剖面、低损耗和对电磁波优秀的操控能力，在许多方面都有应用，例如波束偏转[4]、超薄透镜[5]和探测成像[6]等。超表面对于圆极化波的调控中，最常见的方式是引入几何相位[7-12]，即当单元结构旋转时，在其反射的同极化分量或透射的交叉极化分量中引入与旋转角相关的相位。然而，由于左右旋波束在形式上互为共轭复数，导致相位响应为相反数，极大地限制了超表面的应用。因此，将左右旋波束进行解耦对其进行独立调控是十分必要的。

目前常见的圆极化波解耦方法主要有2种：一种是将传播相位和几何相位相结合[13-15]，传播相位通过强共振来改变，调整超表面对x和y方向上线性相位响应的同时使其具有恒定的相位差，以构造具有不同初始圆极化相位响应的单元，之后通过几何相位对左右旋波束相位进行相长或相消；另一种是将手性相位和几何相位结合[16-17]，利用手性结构的圆二色性改变特定旋向波束的相位，但往往会导致正交旋向波束的幅度很低[18]。这2种方法都需要同时考虑2种相位响应，在设计上较为繁琐。

本文提出了一种手性辅助单元，利用圆弧结构将不同极化波束激发的电流束缚在不同位置，通过改变弧长可以独立地调节左旋或右旋圆极化波束的同极化反射相位。基于此单元分别设计了波束偏转超表面和涡旋波束激发透镜，结果表明左旋和右旋波束均能独立工作，为圆极化波解耦提供了一种新的方案。

1 单元设计

单元结构如图1所示，这是一个旋转对称结构，对角圆弧的张角相同。单元周期为Px=Py= 10 mm，圆弧的半径为r=3.5 mm，圆弧的宽度为wce= 0.5 mm。通过2个分离的带条将左右半区的圆弧分隔开，带条的宽度wl= 1 mm，2个带条间的缝隙为ws= 0.4 mm，介质厚度为h= 3.0 mm，介电常数为εr= 3.0，下方为金属地板。该单元通过改变圆弧的张角α和β，可以分别改变左旋和右旋圆极化波束的反射相位。张角的变化范围为0°～180°，需要注意的是，2个张角之和必须小于180°，当2个圆弧闭合时，该单元变成左右对称单元，失去手型相位能力。首先分析该单元在左右旋波束入射下的电流分布特性。

图1 手性单元示意

在圆极化波垂直入射下，单元表面的电流分布如图2所示，仿真结果由CST微波工作室计算得到。由图2可以看出，对于左旋圆极化电磁波，与α角相关的圆弧有较强烈的电流分布；对于右旋圆极化电磁波，与β角相关的圆弧有较强烈的电流分布，其余位置电流相对很小，可以忽略不计。电流被束缚在圆弧上，以特定的路径流动，且圆弧长度会影响电流的大小。与此同时，与之相连接的带条上仅在临近处有较强电流，距离圆弧超过一半位置处电流减弱。由于电流在单元结构上具有较为独立的分布，因此当圆弧张角改变时，只会较大程度地影响一种旋向波束的相位响应，而对其交叉极化波束的影响很小。

(a) 左旋圆极化波

改变圆弧的张角，在左旋和右旋圆极化波分别垂直照射下，对单元的同极化反射幅度和相位进行分析，如图3所示。

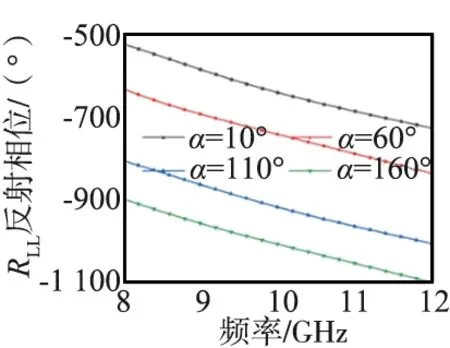
(a) RLL反射相位

其中RLL和RRR分别指在左旋/右旋圆极化波入射下的同极化反射波束。单元的张角β= 10°，张角α在10°～160°变化，图中给出了以50°为梯度变化时的同极化反射系数。可以看出，当张角α在此范围变化时，RLL相位的响应能覆盖360°的相位范围，而RRR相位相对稳定，在10 GHz处变化小于10°，而在8～12 GHz频段范围内的变化量小于30°。此外，单元的RLL和RRR同极化反射幅度响应相同，且均能维持较高水平，在9～12 GHz范围内反射幅度大于0.9，可以极大程度地抑制反射中的交叉极化分量。需要注意的是，由于上下2个圆弧的半径相同，因此2个张角之和无法达到180°，导致2个正交圆极化波束无法独立实现360°相位覆盖，采用将单元旋转90°，引入180°的几何相位，2个张角将同时减小，能够满足左右旋波束相位独立覆盖的要求。

最后，对斜入射下单元的反射特性进行了分析。同样固定张角β= 10°，分别改变圆弧张角α，使其分别为10°和160°。由于左旋圆极化波和右旋圆极化波的同极化反射幅度相同，因此本文以RLL的反射系数变化为例进行分析。左旋圆极化波的入射角度在0°～45°变化，RLL的反射相位和反射幅度变化如图4所示。由图4可以看出，当斜入射角度发生变化时，RLL的反射幅度变化很小，维持在0.9以上。而反射相位会随着倾角增加而增加，这是由于波程在斜入射下增大导致的，反射相位总体在9～12 GH范围内维持线性变化，结果表明该单元在0°～45°斜入射下具有较好的角度稳定性。

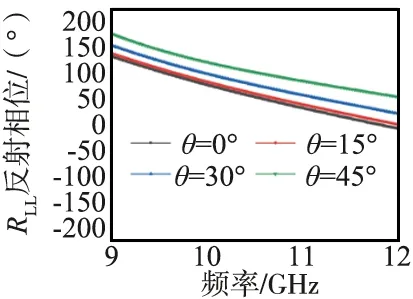
(a) α=10°的RLL反射相位

2 圆极化解耦超构表面

2.1 左右旋独立偏转

首先基于上述单元设计了左右旋独立偏转超构表面以验证所提出方法的有效性。相位梯度的计算基于广义斯涅耳定律[19-21]，通过在介质分界面上引入波长尺寸的相位突变单元，引起电磁波在传播路径上产生相位突变，从而改变电磁波的原始路径，控制波束波前。超表面上的相位排列为：

(1)

式中，nt和ni为媒质的折射率，由于超表面两侧为空气，因此均取值1；l0为空气中电磁波长；dx为沿着分界面上的距离；dj为沿着分界面上的相位变化量。根据广义斯涅耳定律，每个单元对左右旋波束进行独立的相位设计。对左旋圆极化波，相位梯度为0°，-120°，-240°，而对右旋圆极化波，相位梯度为0°，-90°，-180°，-270°，两两组合一共有12种不同参数的单元。在CST软件中对一维阵列进行仿真，x方向边界条件设置为开放边界条件，共有12个单元，以模拟真实环境。由于y方向没有相位梯度，因此设置成周期边界条件以模拟无限大平面。入射波分别设置为左旋圆极化波和右旋圆极化波，入射方向为垂直入射。仿真12 GHz下的远场方向图如图5所示。由图5可以看出，左旋圆极化波的偏转角度为54°，而右旋圆极化波的偏转角度为38°，与理论值相吻合，实现了对左右旋圆极化波进行独立的波束偏转。仿真结果表明，该单元可以实现圆极化波的解耦。

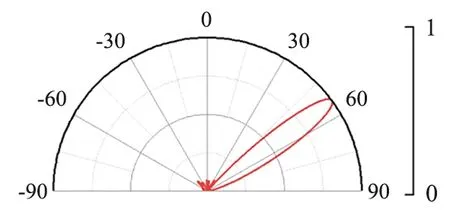
(a) 左旋圆极化波入射的反射同极化分量

2.2 涡旋波束激发

具有轨道角动量的涡旋波束由于不同模式之间具有相互正交性，可以在一定程度上提升信道容量，受到了广泛关注[22-27]。在轨道角动量模式复用中引入电磁波极化复用可以进一步提升信道数量，传统的方法是引入2个正交的线极化波，由于x极化和y极化本身具有可独立调控电磁波的特性，因此只需分别进行涡旋波束相位设计即可。但是圆极化波则不同，由于左右旋波束形式上的相关性，如果仅是在超表面上排列涡旋相位，左旋圆极化和右旋圆极化所激发出的涡旋波束携带有相反的拓扑电荷数。因此，对圆极化涡旋波束的解耦也是十分有必要的。

基于提出单元设计携带有不同拓扑电荷数的涡旋波束超表面。涡旋相位分布与单元所在方位角相关，相位计算依据：

φ(x,y)=l·arctan(y,x)，

(2)

式中，(x，y)表示单元所在坐标；l表示拓扑电荷数，可以为任意整数，这里对左旋圆极化波取l= -1，对右旋圆极化波取l= -2。为了降低设计圆极化独立涡旋透镜的复杂度，对单元的反射相位响应进行了离散编码，将相位以90°为梯度进行离散，相位分布表示如下：

(3)

超表面阵列的大小为200 mm×200 mm，单元数量为20×20个。利用CST软件进行远场仿真，边界条件设置为开放边界条件，入射波分别设置为左旋和右旋圆极化平面波。10 GHz处的远场同极化波方向图如图6所示。从远场方向图中可以清晰观察到波束呈圆环状，且中心处无能量。对于左旋入射波，相位从0°～360°顺时针变化；对于右旋入射波，相位则顺时针变化了2次。远场波束的幅度和相位均证明了此时辐射的同极化波束为涡旋波束，且携带拓扑电荷数与预设值相符，证明了所提出的单元可以实现左右旋圆极化波的极化复用与轨道角动量模式复用结合，进一步验证了提出方单元对圆极化波的解耦能力。

(a) 左旋圆极化波入射的反射同极化分量

3 结束语

本文提出了一种圆极化解耦手性单元，与普通的圆极化解耦单元不同，不需要引入传播相位或手性相位对PB相位进行补偿。该单元利用不同旋向的圆弧结构对左右旋圆极化波束具有不同响应的特点，可以独立对圆极化波束的相位进行调节，同时，对其交叉极化的相位影响可以忽略不计。通过设计左右旋圆极化波束独立偏转以及激发携带不同轨道角动量模式数的涡旋波束进行了验证。仿真结果表明，左右旋波具有不同的偏转角度和携带不同的涡旋波束拓扑电荷数，证明了单元设计的可行性。该方法也可以用于汇聚、成像等其他功能的应用中。