随机波作用下伞式吸力锚基础局部冲刷演变分析❋

赵 真， 胡瑞庚， 刘红军,2❋❋， 冷 浩

(1. 中国海洋大学环境科学与工程学院， 山东 青岛 266100； 2. 海洋环境与生物教育部重点实验室， 山东 青岛 266100)

近年来，风能作为储量巨大的绿色能源得到了广泛的关注，风力发电有着开发区域大、海上风湍流强度低、受土地影响小等优点[1]。随着建设海洋强国战略的实施，海上风机得到迅速发展，同时推动了海上风机基础的发展。吸力锚基础是一种顶部有排水孔、下部开放的基础[2]，具有建设成本低、运输方便、可重复使用等优点，可分为筒型、双筒型基础，后经过李大勇团队改良，设计出裙式吸力锚基础[3]，具有更好的防冲刷效果。李洪江等[4]为进一步提升基础的防冲刷性能提出了新型伞式吸力锚基础(见图1)，基础由主筒、筒裙、锚环、锚枝、撑杆、伸缩钩组成，筒裙外侧设有锚枝，进一步提高了基础的抗倾覆能力和抗冲刷能力[5]。

目前针对海上风机基础周围土体局部冲刷已经开展了大量的研究。Sumer等[6]通过多次水槽试验探讨了冲刷深度与KC(Keulegan-Carpenter)数、桩径和波长之间的关系，表明桩前桩侧马蹄形旋涡和桩后旋涡脱落是造成局部冲刷最主要的因素(见图2)。许多学者考虑不同土质、不同波流条件等影响因素提出了多种冲刷深度计算公式[8]。Mostafa等[12]和Zhang等[13]分别通过物理模拟和数值模拟的方法研究了多根桩在单向流条件下的冲刷特征。Yu等[14]进行了波流作用下筒形基础冲刷物理模型试验，表明波流共同条件比仅波浪或仅水流条件引起更大的冲刷范围，但未必会产生更大的平衡冲刷深度。刘德良等[15]研究了波流作用下单桩基础周围局部冲刷，并分析了波高和流速对冲刷特征的影响。Schendel等[16]研究了潮流作用下水流深度和速度的同时变化对单桩基础冲刷孔发展的影响。

综上可知，针对基础周围土体局部冲刷的研究主要集中在单桩基础，而对吸力锚基础局部冲刷方面的研究较少，而且针对吸力锚基础的相关研究多在规则波(如Airy波、Stokes波等)条件下进行，随机波浪作用下吸力锚基础局部冲刷的模拟研究很少。因此，本文基于JONSWAP随机波浪谱，对随机波浪作用下伞式吸力锚基础(USAF)的局部冲刷特征进行研究，首先探讨了基础周围流场变化规律和冲刷演变模式，在此基础上进一步分析了有效波高、水深两个因素对基础局部冲刷演变的影响规律。

1 模型建立

基于流体动力学软件Flow-3D建立海床-吸力锚-波浪相互作用模型。利用COMSOL软件建立实际尺寸的伞式吸力锚模型，采用VOF法描述水体自由面，通过固定欧拉网格捕捉冲刷形态随时间的变化，采用JONSWAP波浪谱函数模拟随机波，模拟不同波浪要素和水力要素条件下伞式吸力锚的局部冲刷特征。

1.1 控制方程

1.1.1 动量方程 利用能过方程可以描述流体在(x,y,z)方向的速度分量(μ,ν,ω)：

(1)

(2)

(3)

式中：VF为水体体积分数；Ax、Ay、Az分别为t时刻x、y、z方向的流体面积分数；ρ为流体密度；p为流体压强；Gz为加速度分量；fx、fy、fz分别为x、y、z方向的黏滞加速度分量。

1.1.2 质量连续方程

(4)

式中：ρω为流体密度；Rdfj为湍流扩散项。

1.1.3 流体自由面方程 采用VOF法描述流体自由面，即：

(5)

式中VF为扩散系数。

1.1.4 湍流模型 考虑到湍流旋涡的影响和较小雷诺数等因素，采用RNGκ-ε模型进行冲刷模拟，此模型可以更好的模拟绕流和旋涡脱落等流体紊动。

(6)

(7)

式中：κT为紊流动能；εT为湍流能耗散率；T为周期；GT为平均速度梯度产生的湍流能；PT为湍动能方程产生的湍流动能；CDIS1、CDIS2、CDIS3为无量纲参数。

1.1.5 泥沙输送模型 考虑到推移质的运移，采用Meyer推移质输沙率计算公式：

Φs=βs(θ-θcr)1.5Cb,s。

(8)

式中：Φs为推移质输沙率；Cb,s为颗粒体积分数；βs为推移质系数；θcr为临界希尔兹数；θ为希尔兹数。

推移质体积输沙率公式为：

(9)

式中：qb,s为推移质体积输沙率；ds为泥沙粒径；g为重力加速度。

临界希尔兹数为：

(10)

考虑到波浪、坡度等因素的影响，对临界希尔兹数进行修正[17]：

(11)

式中：θcr为临界希尔兹数；Ψ为水流方向与上坡方向的夹角；φ为休止角；β为河床坡度。

1.2 模型参数

建立实际尺寸的伞式吸力锚模型，并进一步建立海床-吸力锚-波浪相互作用模型。伞式吸力锚模型设计尺寸如表1所示，海床-吸力锚-波浪相互作用模型建立参数如表2所示，海床土体参数为海域所取土样参照标准通过室内筛分、环刀法等测得。

伞式吸力锚基础锚枝结构较小，为准确描述其冲刷特征，本文作者采用细小尺寸的网格划分，并在模型周围进行网格局部嵌套(见图3(b))，增加网格密度使局部嵌套范围内网格数量达到110万，建立海床-吸力锚-波浪相互作用模型(见图3(a))。边界条件设置为：模型入流处(Xmin)为波浪边界；出流处(Xmax)为出流边界；两侧(Ymin,Ymax)为对称边界；底部(Zmin)为墙边界；上部(Zmax)为对称边界。

1.3 波浪参数

实际条件下的海浪并不是规则的，因此进行随机波浪作用下的冲刷模拟更加符合实际。本文根据“联合北海波浪计划”观测所得的JONSWAP谱来模拟随机波，波浪谱函数为：

(12)

式中：α为无因次常数；ωm为谱峰频率。

γ为谱峰提升因子，本文取γ=3.3；σ为峰形参数，当ω<ωm时，一般取σ=0.07；当ω>ωm时，一般取σ=0.09。

一般取

α=0.007 6(gx/U2)-0.22，

(13)

ωm=22(g/U)(gx/U2)-0.33。

(14)

式中：x为风区长度，U为10 m高处的平均风速。

该谱参照P-M谱的形式提出，可以通过改变平均风速、风区长度等变量模拟不同有效波高的波浪，还能够模拟中等风况和有限风距情况下不同成长阶段的风浪，应用非常广泛[18]。

2 模型验证

为验证数值模型的可靠性，将建立的冲刷模型与Khosronejad等[19]的冲刷试验结果进行对比验证。建立相同条件下的模型参数，相关参数见表3，得到其桩周冲刷深度时程演变曲线(见图4)。图中可以发现数值模拟得到的结果在10 min之前略小于Khosronejad试验结果，随后冲刷发育加快，最终冲刷深度与试验结果基本一致，总体的吻合效果较好。然后与Melville等[20]试验结果对比验证流场特征(见图5)，可以发现本研究数值模拟得到流场特征与Mdvilleh试验所得的流场特征基本吻合，水体在经过桩周后产生流线压缩，基础后方产生较明显的旋涡。以上说明本文建立的数值模型能够较好模拟桩周土体的局部冲刷，并进一步研究桩周土体局部冲刷特征。

3 计算与分析

本文结合某海域风区资料[21]，设计9组不同有效波高和水深的组合进行模拟，具体试验组次如表4所示。通过试验分析以下几个部分：(1)随机波作用下基础近底流体的湍流强度特征及其发展变化。(2)波浪作用过程中基础周围流场变化，以得到随机波作用下的流场特征。(3)冲刷时程演变，分析其局部冲刷演变过程和最大冲刷深度。(4)有效波高和水深对局部冲刷演变的影响规律。(5)锚枝防冲刷效果。

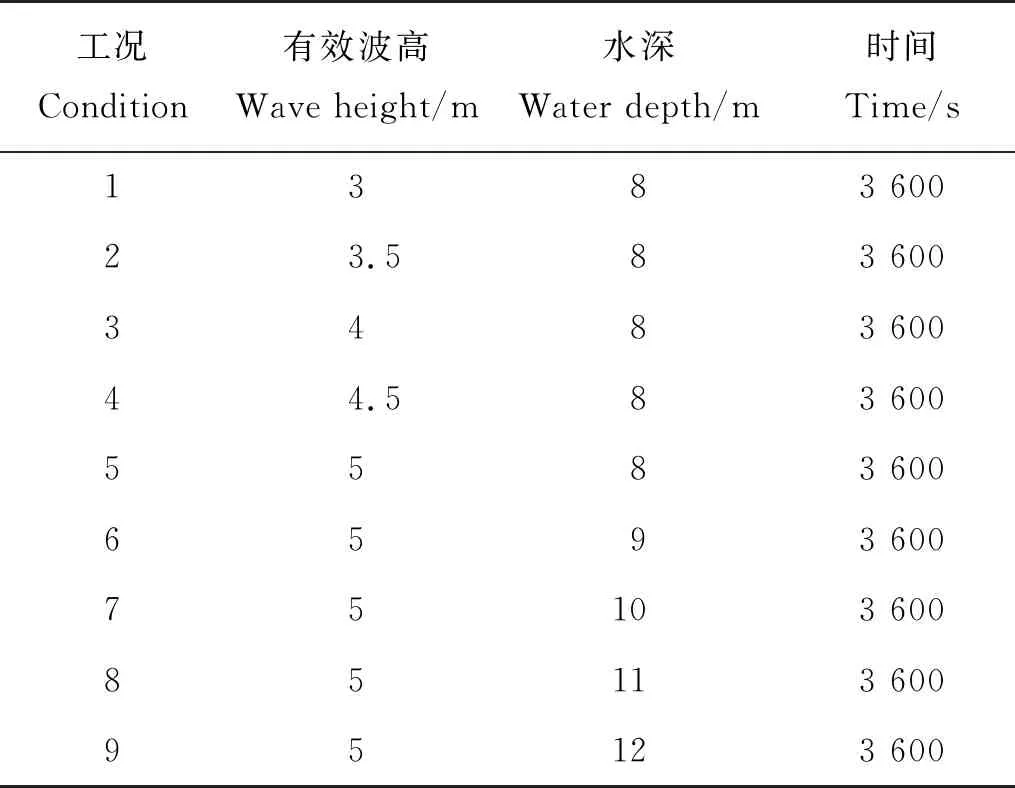
表4 试验分组

3.1 湍流强度特征

基础周围局部冲刷的形成是湍流和旋涡综合作用的结果[22]，因此湍流强度的变化会对冲刷产生明显影响。选取工况5中三组波浪作用下近底水流的湍流强度进行分析(见图6)。可以发现波浪的湍流强度在桩前0～3 m区域内达到最大值，最大区域围绕桩前呈弧形，锚枝正上方的湍流强度略大于锚枝间。从主筒筒前到筒后湍流强度逐渐减小，因此筒前水体湍动能非常大，对锚枝之间土体冲刷产生剧烈影响。侧后方湍流强度较弱，筒前冲刷运移的土体在此沉积并持续对周围流场产生影响，泥沙不断淤积。随着波峰的前进在筒后6～12 m处也产生了湍流强度较大的区域，分析认为是波浪作用使基础两侧水流收缩集中，动能增加，绕过基础旋转，在筒后形成范围较大的尾涡，尾漩不断的从基础两侧释放出来，在基础下游形成旋涡脱落，这种现象增加了水体对海床的扰动作用，加剧了筒后区域的冲刷和淤积，导致桩后方冲刷坑的发展。

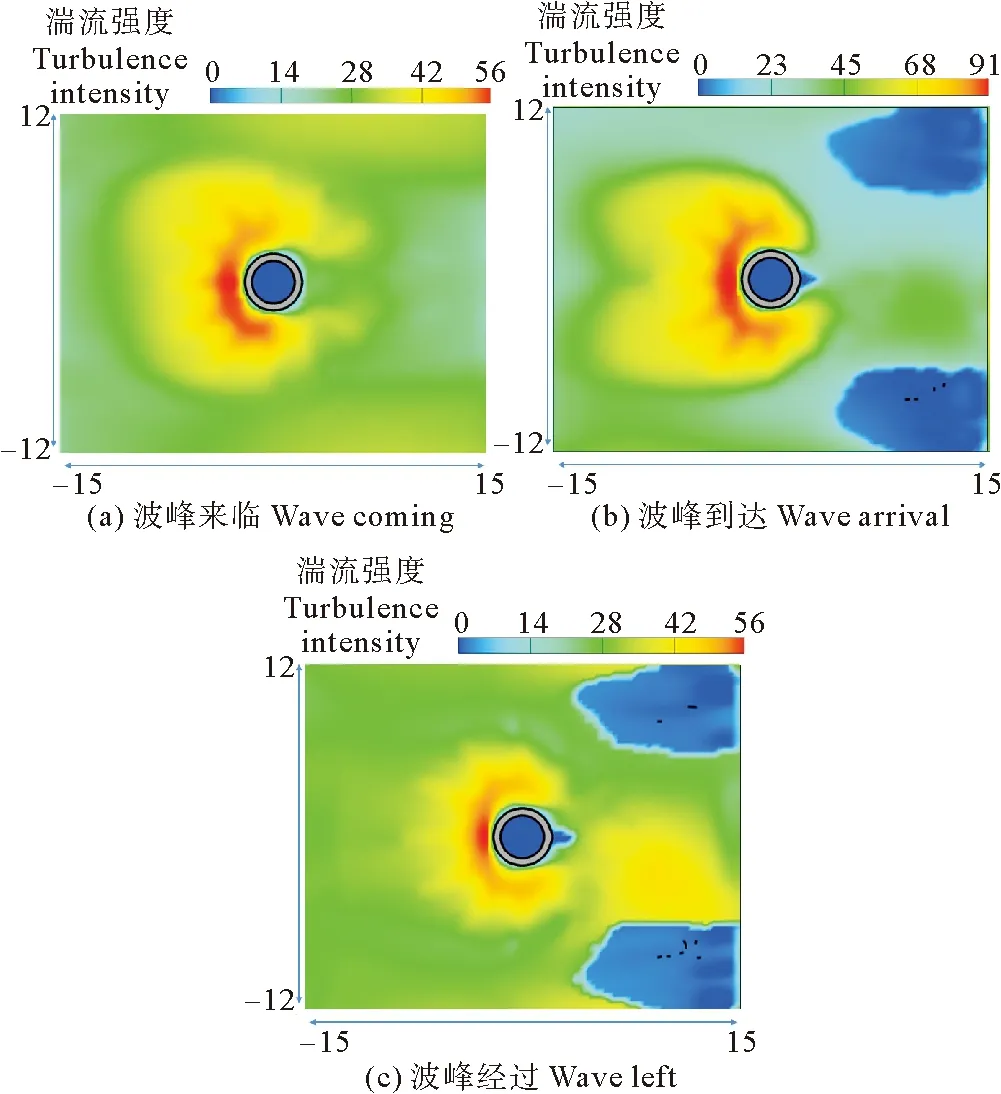
图6 基础周围湍流强度特征

3.2 流场特征

取筒侧剖面三个不同时刻的水体运动速度矢量分析其流场特征(见图7)。可以发现波峰来临前上部水质点向上运动且流速较快，最大达到2.46 m/s，势能增加，近底水质点水平移动且流速较慢。波峰经过后，水质点迅速下沉，筒侧流线收缩，外部水体向上运动，最终产生马蹄形旋涡，从而产生向下翻滚的涡漩。水体流线压缩下沉和旋涡的影响会加剧水流紊乱状态，增强对土颗粒的搬运能力，使土体所受剪切应力增大，导致泥沙启动形成冲刷坑。

图7 筒侧流场特征

3.3 冲刷时程演变

冲刷演变图像和时程演变曲线能够直观的反映桩周局部冲刷发展变化。取工况5条件下基础周围土体最大冲刷深度、淤积高度时程曲线(见图8)和在600、1 200、1 800、2 400、3 000、3 600 s六个时刻的冲刷图像(见图9)，分析其总体冲刷特征和冲刷演变过程。因而可知筒前锚枝处和筒后13～20 m区域最先产生冲刷，且这两处分别受到马蹄形旋涡和旋涡脱落影响，水流紊动剧烈。随后所有锚枝都开始被冲刷，土体被搬运到筒侧后方沉积。前2 400 s局部冲刷不断发展，之后冲刷坑和淤积土体基本保持稳定，最大冲刷深度出现在筒前45°两锚枝之间，为0.679 m，结合图6、7可知此处正是流线下沉和马蹄形旋涡综合作用最强处，水流在迎流侧锚枝之间的紊动非常剧烈，且水体对基础周围土体产生明显剥蚀作用，导致迎流侧锚枝之间的冲刷最为明显。最大淤积高度出现在筒侧后方，最大淤积高度为0.404 m。

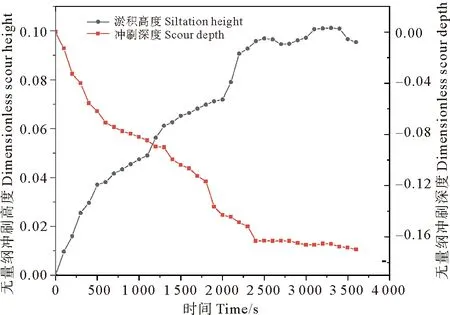
图8 工况5最大冲刷深度、淤积高度时程曲线

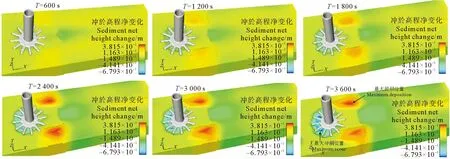
图9 工况5不同时刻冲刷图像

为分析局部冲刷发展过程，取基础主筒前3 m、筒后3 m、筒后10 m处的剖面(见图3(c))分析其土体高程净变化(见图10)。分析可知，筒前3 m处锚枝之间冲刷剧烈，冲刷坑深度随着时间的增加一直在增长，最大达到0.645 m。结合最大冲刷深度时程曲线可知虽然最大冲刷深度在2 400 s左右已经达到最大值，但是冲刷坑的范围仍然在扩大，马蹄形旋涡下沉会对冲刷坑产生持续作用。筒后3 m处锚枝之间的冲刷深度较小，2 400 s左右已经达到平衡，最大冲刷深度为0.267 m，冲刷剖面为倒三角形，只有少部分土体启动运移。最大淤积高度为0.247 m，主要集中在筒侧6～10 m之间。筒后10 m处淤积基本达到最大值，最大淤积高度位于筒侧6 m处。前期淤积速度较快，随后速度变缓，在2 400 s左右达到平衡。正后方有比较小的冲刷现象，冲刷深度在0.152～0.106 m之间。因此伞式吸力锚迎流面处冲刷较为剧烈，其迎流面锚枝之间的防冲刷设计非常重要，后续需要进一步做好防冲刷设计。

图10 不同剖面土体高程净变化

3.4 不同有效波高和水深条件对局部冲刷的影响

由文献[6-7]可知KC数是波浪作用下圆柱形桩周土体冲刷剧烈程度的决定因素，而其重要参数UW是关于波高和水深的函数，因此有效波高和水深的变化是影响局部冲刷的重要因素。本文分别控制了5种不同有效波高和5种不同水深的变量进行分析，探讨其条件变化对冲刷特征的影响。

3.4.1 有效波高变化的影响 不同有效波高在3 600 s时的冲刷图像(见图11)可以直观的反映冲刷特征的差异，由图中可以发现随着有效波高的增加，筒前特别是筒前45°锚枝之间的冲刷逐渐剧烈，淤积继续向侧后方发展，中间出现明显的水流通道。正后方出现明显的冲刷区域，土体被运移到远处沉积。

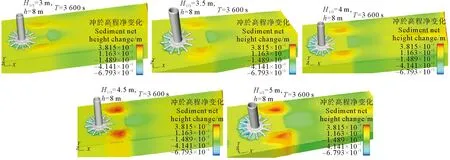
图11 不同有效波高下3 600 s冲刷图像

取工况1～5条件下基础周围土体最大冲刷深度和淤积高度时程曲线(见图12)，可知有效波高越高，局部冲刷演变过程越剧烈，最大冲刷深度越大。有效波高为3 m时，最大冲刷深度为0.411 m；有效波高为5 m时，最大冲刷深度达到0.679 m。冲刷演变过程具有一定的规律性，泥沙启动后冲刷处于迅速发展阶段，然后趋于稳定，最终在2 400～2 700 s达到冲刷平衡，最大冲刷深度基本不再变化。筒侧后方的淤积变化也非常明显，五种条件下的总体发展趋势相似，在2 400～2 700 s左右达到平衡。可以发现有效波高为5 m时2 000 s左右有一个明显区间淤积高度迅速增加，分析认为有效波高越高，波浪能量越大，发展越不稳定。有效波高为5 m时最大淤积高度为0.404 m，3 m时最大淤积高度为0.221 m。

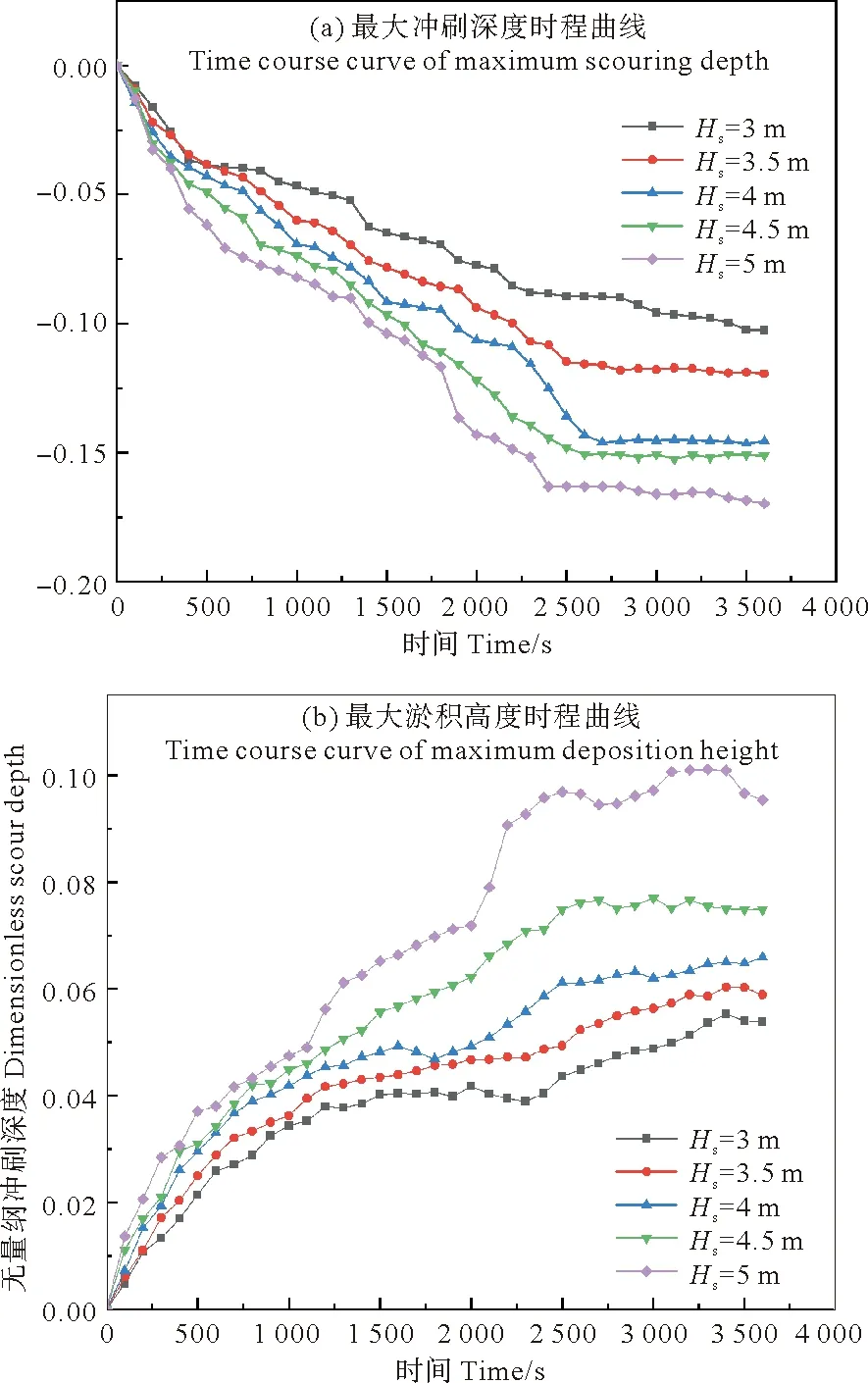
图12 不同有效波高下的时程曲线

3.4.2 水深变化的影响 取工况5～9条件下3 600 s局部冲刷示意图(见图13)进行分析，可以发现试验范围内水深的变化对局部冲刷的影响非常显著。随着水深从8 m增加到12 m，筒前锚枝之间的冲刷深度变化不大，侧后方的淤积程度变化明显。水深从8 m增加到10 m时，筒侧后方的淤积量和最大淤积高度不断增加，10 m水深时达到0.711 m，随后逐渐减小。后方逐渐产生了明显的冲刷坑并向后不断发展，当水深在11、12 m时，最大冲刷深度出现在筒后方13 m左右处的冲刷坑内。

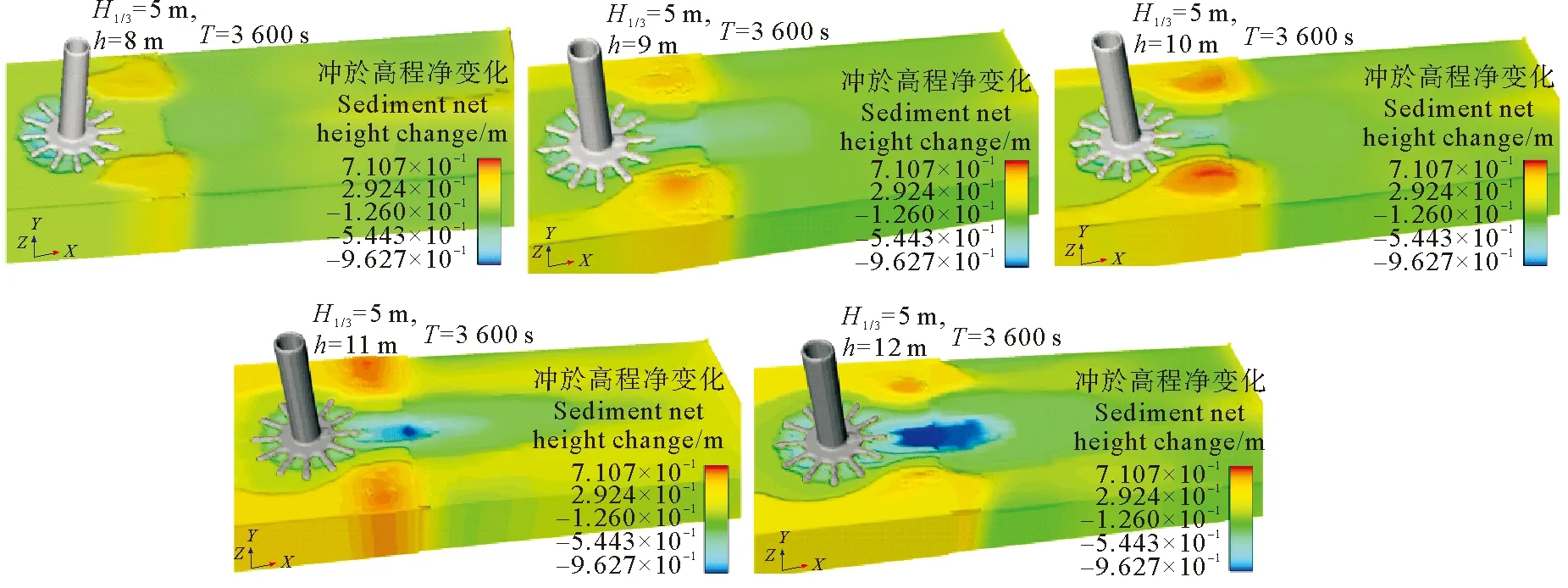
图13 不同水深下3 600 s冲刷图像

取基础周围最大冲刷深度和淤积高度时程曲线如图14所示，可知5种水深下最大冲刷深度时程曲线变化基本一致，水深8、9 m时最大冲刷深度时程曲线基本一致，平衡时最大冲刷深度在0.656～0.704 m之间；水深12 m时冲刷演变最剧烈，得到最大平衡冲刷深度。结合图13可知8、9、10 m水深时最大冲刷深度的演变在筒前锚枝之间，而11、12 m水深时出现在后方的冲刷坑内。五种水深条件下达到冲刷平衡的时间都在2 400 s左右。水深8～10 m期间淤积速度不断加快，最大淤积高度不断增加。在水深8、9、10 m时，最大淤积高度分别达到0.404、0.595和0.711 m，随着水深继续增加淤积速度也在缓慢增加，但是达到冲刷平衡所需的时间有所减少，最大淤积高度逐渐降低，在水深11和12 m时最大淤积高度分别为0.614和0.547 m。结合冲刷图像可知在水深大于10 m后筒侧后方的淤积逐渐向后方发展，淤积范围逐渐扩大，土体不断向后方运移，从而导致最大淤积高度逐渐降低。

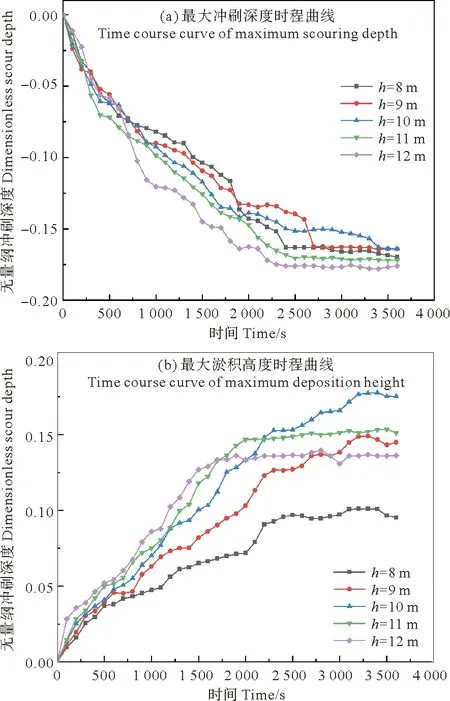
图14 不同水深下的时程曲线

3.5 锚枝冲刷防护效果分析

为验证锚枝的防冲刷效果，取工况9条件下伞式吸力锚基础和裙式吸力锚基础周围3 600 s局部冲刷等高线(见图15)，可以发现两种基础总体的冲刷范围基本一致，但是锚枝的存在对伞式吸力锚基础周围一定范围内的土体起到较好固定作用，在锚枝之间仅有轻微的冲刷。相比之下裙式吸力锚基础桩前桩侧产生了明显的冲刷坑，冲刷坑深度和范围都较大。两种基础形式后方都产生了明显冲刷坑，但是锚枝一定程度上减小了冲刷坑范围，抑制了冲刷坑的发展。综上可知伞式吸力锚总体防冲刷性能较好，能够起到更好的防冲刷效果，但值得注意的是迎流面处冲刷较为剧烈，因此迎流面锚枝之间的防冲刷设计非常重要，后续需要进一步改进。

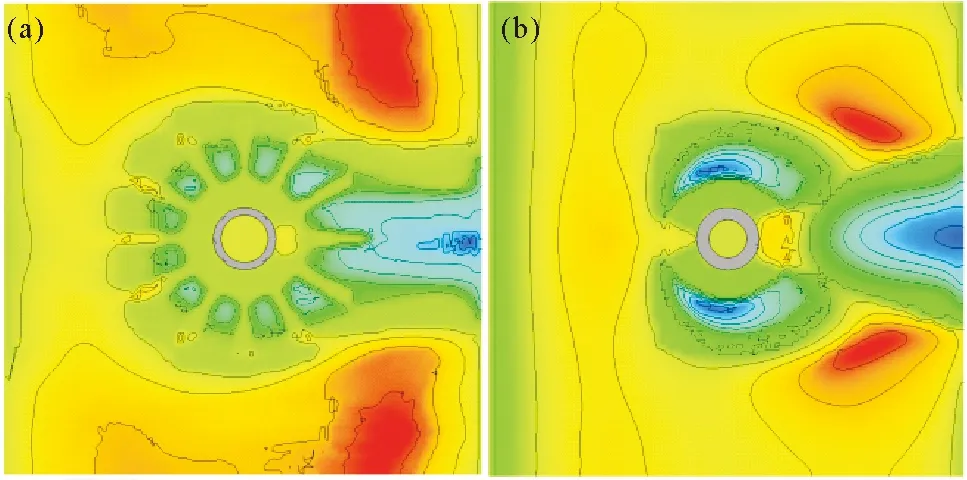
图15 伞式(a)、裙式(b)吸力锚等高线图

4 结论

(1)基础的设置加剧了主筒前0～3 m、筒后6～12 m范围内的湍流强度，水流紊动增强了对土颗粒的搬运能力，导致泥沙起动产生冲刷，锚枝的存在能够减少基础周土体的运移，提高周围土体稳定性。

(2)有效波高的增加导致主筒前45°锚枝之间的冲刷程度加剧，使旋涡脱落具有的能量增大，淤积范围后移。水深的变化对筒前马蹄形旋涡的影响不大，对旋涡脱落影响明显，随水深的增加后方产生逐渐增大的冲刷坑，10 m后最大冲刷深度位于冲刷坑内，水深8～10 m范围内淤积高度不断增加，随后逐渐降低。

(3)伞式吸力锚基础的防冲刷性能总体较好，但是还可以针对其筒前锚枝冲刷剧烈和筒后冲刷坑较大的现象进行进一步优化，比如进行化学固化和抛石等方法，未来可以进行优化后防冲刷效果分析。