杂散电流下管道电参数波动特征的傅里叶分析

1 傅里叶变换应用现状

傅里叶变换是信号分析与处理最常用的方法之一，它能够将不易处理的时域信号转换成便于统计分析的频域信号，广泛应用于图像处理、数据采集、控制工程和雷达探测等方面，对工业发展起到非常大的作用。快速傅里叶变换(FFT)是在离散傅里叶变换(DFT)的基础上形成的快速算法，它将计算的时间复杂度由

(

)降低至

(

log

)，其中

是与时间相关的参数，同时也要求快速傅里叶变换的样本点数量为2的整数次幂，因此FFT也称为基2快速傅里叶变换。游盈萱等

利用傅里叶变换对调制后的光信号进行处理，分解出各光源的频率和振幅后，剔除了杂波数据，优化了三点定位算法，提出了一种响应快速、定位精确的可见光室内定位系统。周雪松等

提出了一种基于快速傅里叶变换的天气雷达弱径向杂波识别方法，通过快速傅里叶变换后的频谱分析很好地识别了异常回波，将周期性变化的异常回波剔除后大幅提高了雷达的图像质量。刘政委等

提出了一种基于快速傅里叶变换的燃烧动态监测方法，利用快速傅里叶变换得到压力信号的频谱图，提取燃烧不稳定现象的特征，分析压力信号中的不同频段的幅值，并利用在不同频段下相应的限值对燃烧进行动态监测。

2 动态杂散电流干扰规律分析现状

城镇燃气管网受杂散电流干扰主要涉及两种形态，分别是稳态干扰与动态干扰。稳态干扰主要来源于高压输电线、阴保系统之间的干扰，由于多呈现为稳态形式，所以针对其波动特征及干扰规律的分析相对简单。动态干扰主要来源于地铁及电气化铁路，地铁干扰主要为动态直流，能够直接影响管地电位，因此对于地铁干扰规律分析主要通过管地电位进行统计；而电气化铁路产生的干扰主要为动态交流，其干扰形式介于动态直流及稳态交流，对于管地电位的影响相对复杂，因此对于电气化铁路干扰规律分析主要通过管道的交流干扰电压进行统计。目前国内外的防腐工作者为了提取干扰的关键参数已经针对动态杂散电流干扰规律开展了一系列的统计分析。

史海沉钩，以古鉴今。前赴后继的共产党人留给我们宝贵的历史遗产，光荣伟大的革命先辈撒播下纯正的革命种子，这是我们不朽的精神源泉，激励我们不懈地继续追求新时代的中国梦。70年风雨沧桑，镌刻在淮海战役烈士纪念碑上的大字依旧闪闪发光，永垂不朽，激励后人。炮火与鲜血中诞生的共和国在一条光明的大道上坚定前行着，牢记历史，把握当下，淮海战役精神将会在今天焕发出一种新的生命力与活力。

针对地铁动态直流干扰波动特征的分析，主要有以下研究进展。刘瑶等

对北京燃气管网受地铁的干扰情况进行分析，通过24 h管地电位的监测数据局部放大发现，受地铁干扰的管地电位由多个小波峰组合而成大波峰，通过对大波峰的时间进行统计，发现大波峰的周期主要处于50～200 s范围内，该区间内的周期相对占比高达75%。朱祥剑等

对北京、上海、深圳、无锡4个城市受地铁干扰的管地电位进行统计分析发现，不同城市的干扰周期分布基本一致，其干扰周期均处于0～300 s范围内，具体某一段干扰周期的占比受各地地铁运行时间间隔的影响略有差异。刘杰等

对某地受地铁干扰的管地电位进行分析，发现每6 min会出现一次干扰峰值，干扰周期与地铁的发车间隔基本一致。董亮等

通过对上海、广州、深圳、武汉4个地区与地铁邻近的管网电参数进行分析，发现其干扰主频率分别为9 mHz、7 mHz、7 mHz、5 mHz，各个城市的干扰主频率差异受行车间隔影响。肖嵩等

对武汉7条轨道交通邻近的管地电位进行傅里叶变换分析，得出50%以上的波动发生在0.005～0.030 Hz，并且多数处于0.01～0.02 Hz及0.02～0.03 Hz。

针对电气化铁路动态交流干扰波动特征的分析，由于其干扰相对复杂及腐蚀风险相对较低，因此相关的研究成果较少，且大部分为规律性研究结论，未能有效提取关键干扰参数。李伟等

通过调研发现电气化铁路在运行过程中会对邻近管网产生交流干扰影响，干扰程度与机车的运行频次、载荷量有较大关系，并且通过高压输电线及铁路对管网的干扰情况分析，发现电气化铁路邻近管网的交流干扰电压及电流密度变化剧烈，且存在明显波动的尖峰。李兴锋等

通过对某段与电气化铁路交叉管线的干扰参数分析发现，电气化铁路对管网的交流干扰电压影响较大，且机车通过越频繁，交流干扰越明显。周宇等

通过对上海某段埋地管道的管地电位傅里叶频域分析，发现测试点的管地电位波动集中在频率50 Hz，进一步确定该管段受部分交流干扰的影响，为干扰源的确定提供依据。程彤等

通过对京沪高铁试运行、正式运行后的相互比较发现高铁发车频率越大、载重量越大，形成的交流干扰显然越大。

3 动态直流干扰特征的傅里叶分析

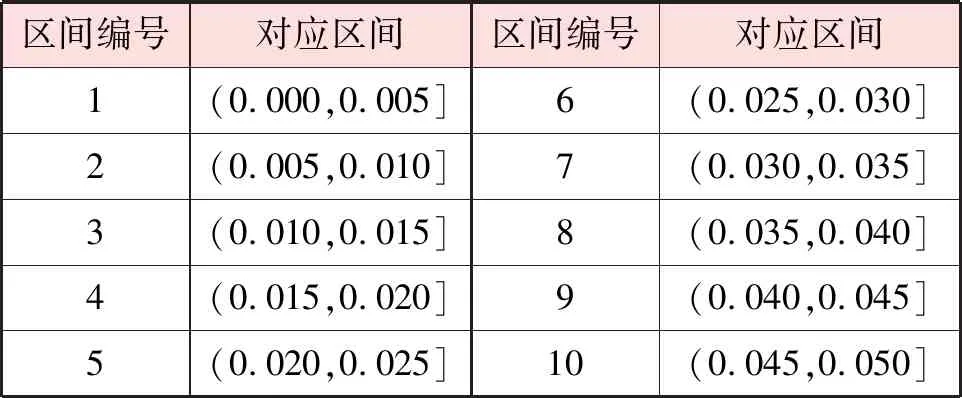
对图2进行固定频率区间的波动幅值相对占比分析，即每0.005 Hz的波动幅值之和占整个区间的波动幅度之和的比例。区间编号见表1，区间值对应单位为Hz，固定频率区间的波动幅度相对占比见图3。

通过uDL-2数据采集器对某段受地铁杂散电流干扰的管地电位进行数据采集，采集时段为15:00至隔天9:00，采集周期为1 s；同时此次目的是为了分析干扰特征及干扰规律，所以主要以波动幅度较大的通电电位为主。不同监测点的管地电位波动见图1。由图所示的3个监测点可以得出，受地铁运行时间的影响，白天测得的管地电位波动幅度明显高于夜间。通过对3个监测点的数据进行分析，统计出在00:40—5:00这一时间段管地电位基本无波动，但该时间明显晚于地铁末班车时间，早于地铁首班车时间，分析原因是地铁停止载客后的维检修及巡线引起的杂散电流。

② 动态交流干扰规律分析

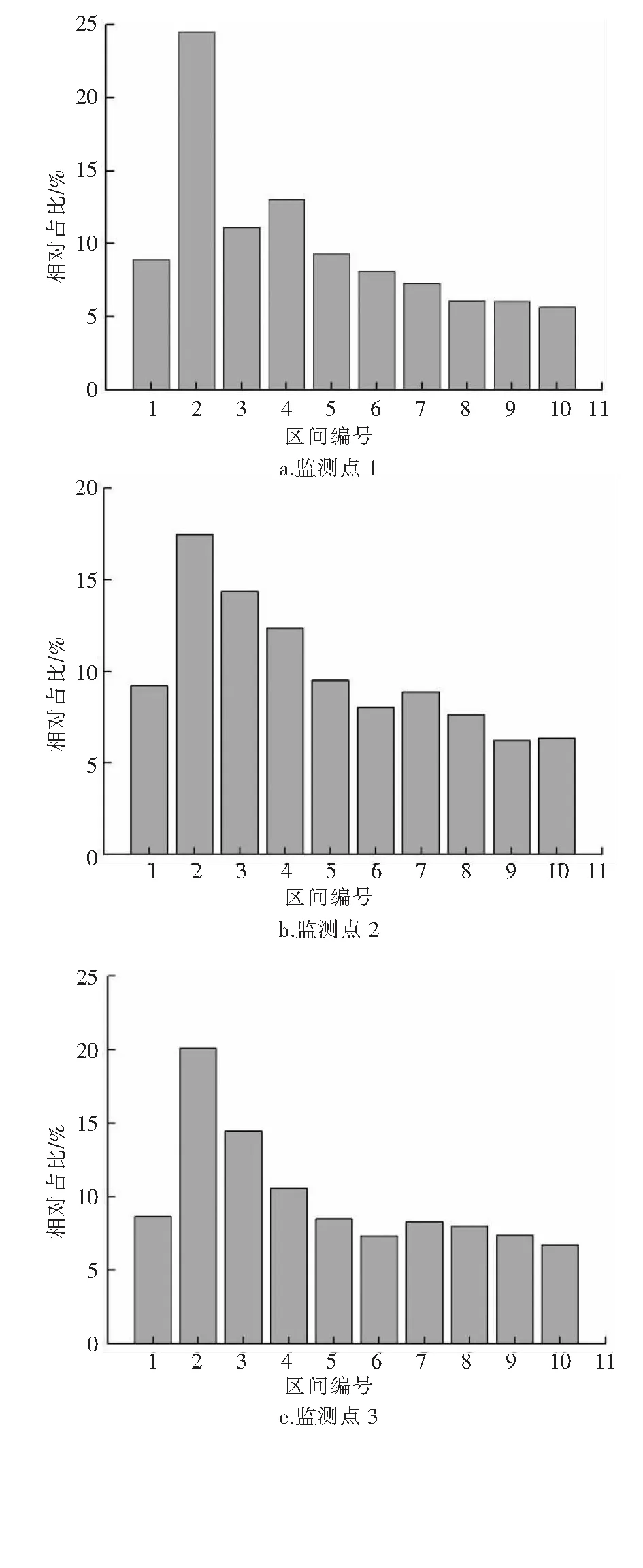
通过uDL-2数据采集器对某段受电气化铁路杂散电流影响的交流干扰电压进行数据采集，采集时段为4月9日12:00至15:00，采集周期为1 s。电气化铁路形成的干扰类似于地铁干扰，大部分为动态波动的特征，但与地铁干扰的差异是其产生的干扰信号为交流信号，分析其对管道的腐蚀规律难度更大。不同监测点的交流干扰电压波动见图4，可以看出，电气化铁路形成的干扰信号的波动频率明显低于地铁，分析其原因是机车的运行时间间隔远高于地铁，相应的杂散电流泄漏频率更低。

① 动态直流干扰特征分析

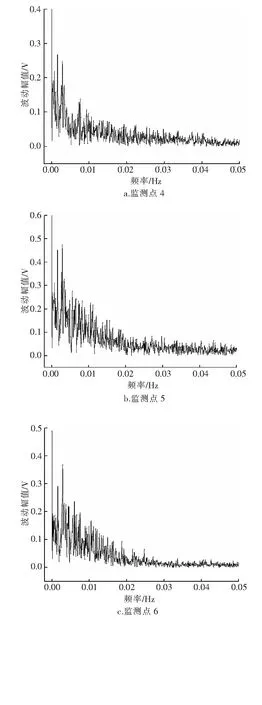
对于动态交流干扰数据，借鉴前文分析地铁直流干扰数据的方法，利用快速傅里叶变换提取干扰周期，从而为实验室模拟实验提供关键参数。不同监测点的快速傅里叶变换频谱图见图5，图中，由于频率为0时的峰值对于此次数据分析无意义，所以图中未完全显示频率为0时的波动幅值。可以看出，在频率0.001 6 Hz、0.002 9 Hz及0.002 9 Hz时信号强度最大，将频率转换为周期后分别为625 s、345 s及345 s，说明电气化铁路干扰的主要干扰周期处于345～625 s。但与地铁干扰的频谱分析不同，地铁干扰有比较明确的波峰，但电气化铁路干扰有多个近似波峰，说明对于动态交流干扰的分析，获得其干扰周期的区间更加合理。

4 动态交流干扰特征的傅里叶分析

① 动态交流干扰特征分析

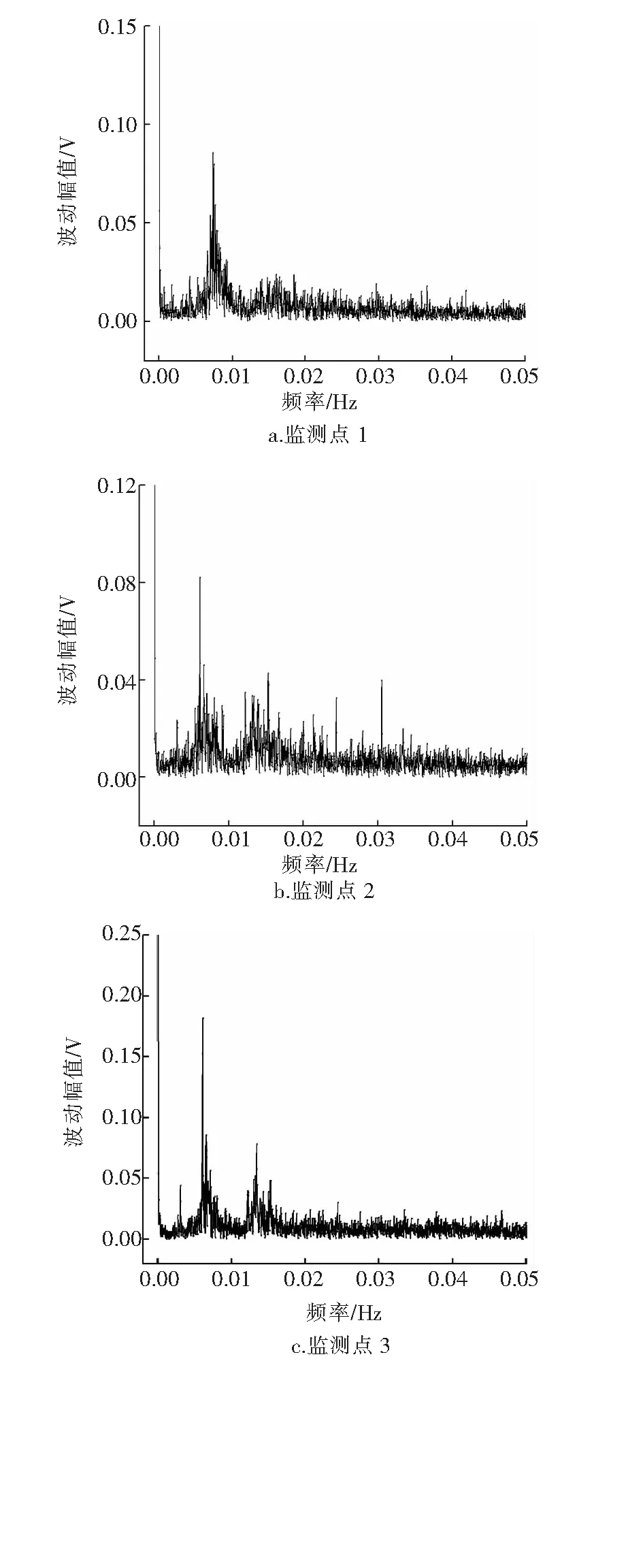
通过对动态杂乱的干扰数据进行统计，分析其干扰规律，获取地铁干扰下的主要干扰周期，从而指导实验室模拟实验参数的选取。利用快速傅里叶变换(应用Origin软件)将干扰数据拆分成多个不同频谱的信号，随后通过筛选最大信号对应的频率，将其转化为主要干扰周期，同时统计固定频率区间的波动幅值占比，明确地铁干扰周期的主要区间。不同监测点的快速傅里叶变换频谱图见图2。图中，由于频率为0时的峰值，对于此次数据分析无意义，所以图中未完全显示频率为0时的波动幅值。对3个监测点做快速傅里叶变换之后，发现在频率分别为0.007 Hz、0.006 Hz及0.006 Hz时信号强度最大，将频率转换为周期后分别为143 s、167 s及167 s，说明地铁干扰的主要干扰周期处于143～167 s。

解析：A选项,标准状况下,三氧化硫是固体,错误。B选项,气体应为SO2和H2的混合气,只有在标准状况下,结论才正确。C选项,CH4分子中C、H原子个数比与状况及CH4的多少无关,正确;D选项,质量与状况无关,11.2g乙烯的物质的量为0.4 mol,1mol乙烯分子中共用电子对数目为6个,故11.2g乙烯中含有的共用电子对数目为2.4NA。

② 动态直流干扰规律分析

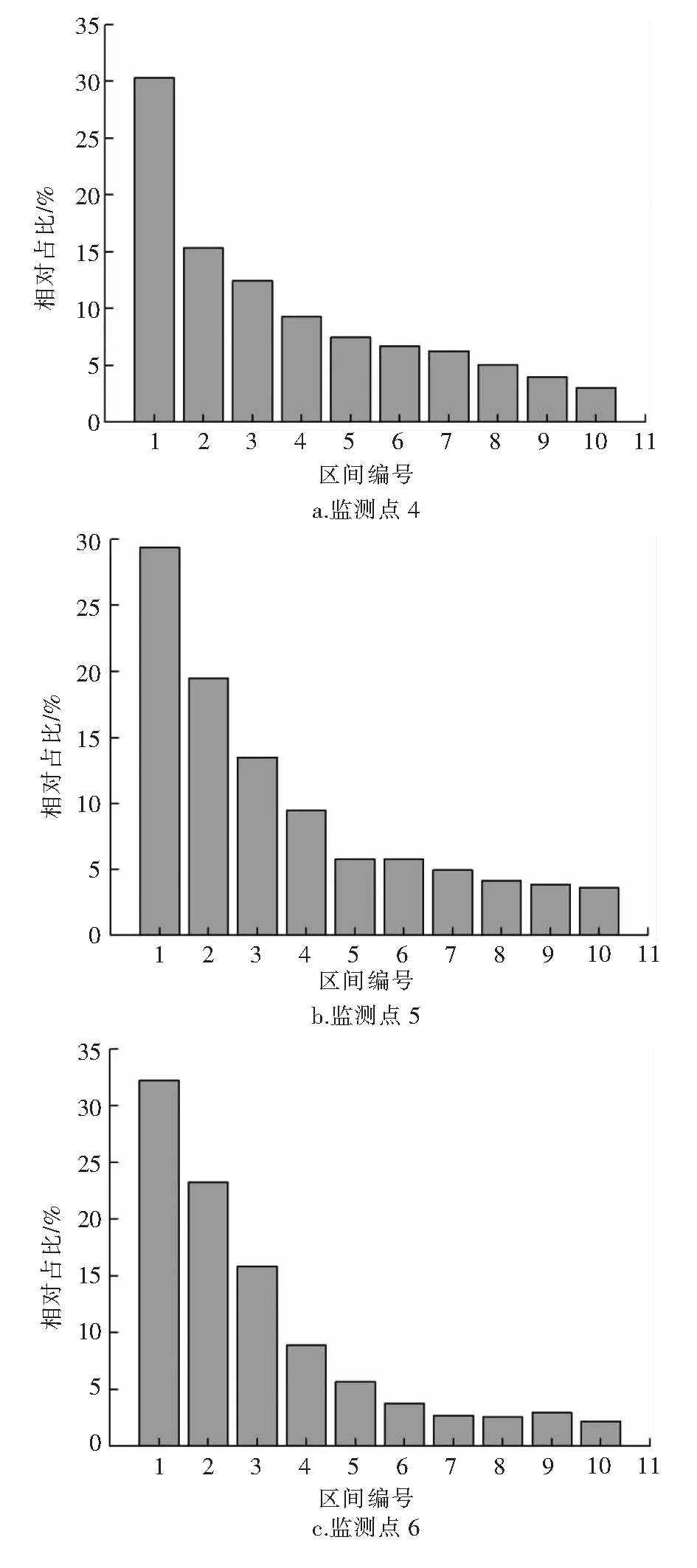
对图5进行固定频率区间的波动幅值相对占比分析，即每0.005 Hz的波动幅值之和占整个区间的波动幅度之和的比例。区间编号见表1，固定频率区间的波动幅度相对占比见图6。可以明显看出，3个监测点的频率区间为0～0.005 Hz时，波动幅值相对占比最高，对应的干扰周期大于200 s。另外频率区间为0～0.010 Hz时，波动幅值相对占比分别为46%、49%及55%，对应的干扰周期大于100 s，说明电气化铁路干扰周期明显高于地铁干扰。

可以明显看出3个监测点的频率区间为0.005～0.010 Hz时，波动幅值相对占比最高，对应的干扰周期区间为100～200 s。另外频率区间为0.005～0.020 Hz时，相对占比分别为49%、44%及45%，对应的干扰周期区间为50～200 s，说明地铁干扰的主要周期集中在该区间内，后续在开展实验室模拟地铁干扰时干扰周期应以50～200 s区间为主。

在美国， Kronospan公司决定进一步增加1.01亿美元对亚拉巴马州牛津的投资，共计达4.63亿美元。该扩张计划最初是在2016年年中宣布的，投资额为3.62亿美元，包括两条强化地板及浸渍纸装饰生产线、一条刨花板及热熔胶合层压生产线，以及合成树脂厂的扩建。

影响建筑物稳定的因素很多,而建筑物沉降作为系统的主要输出信息则是一个具有灰色特征的随机变量，通过分析建筑物沉降数据的特点，结合灰色模型的特征，采用灰色模型来预测建筑物的沉降趋势是可行、有效的方法。传统GM(1，1)模型对于不同数据序列，会出现偏差较大的情况。当原始沉降数据序列为持续增长或者数据变化较大的数据序列时，模型预测结果的偏差就会变大，预测精度普遍偏低［2］。另外，灰色模型是用历史信息来预测将来的信息，所以信息的维数对预测精度也有一定影响，如何合理选择数据的维度是保证预测精度的关键。

5 结论

① 通过快速傅里叶变换分析得出地铁干扰最大信号强度的频率为0.006 Hz及0.007 Hz，主要干扰周期处于143～167 s，大部分干扰周期区间处于50～200 s；电气化铁路干扰最大信号强度的频率为0.001 6 Hz及0.002 9 Hz，主要干扰周期处于345～625 s，大部分干扰周期区间大于100 s。

② 地铁干扰与电气化铁路干扰周期受运行时间间隔的影响，存在一定的差异性，地铁干扰周期明显短于电气化铁路干扰周期，地铁干扰波动频率明显高于电气化铁路波动频率；另外，地铁干扰的主要干扰信号相对更加明显。

长春市九台区文化工作则把文化深入嫁接到旅游事业中。九台区正打造国际多彩文化旅游城，“中国北方四季山地玩都”初步规划有四十二个景区，其中一个国家水利风景区（石头口门水库），两个4A级旅游景区（庙香山滑雪休闲度假区和碧水庄园），旅游景点数量位居全省前列。被评为吉林省第一个旅游标准化试验区，也是“全国旅游综合改革试点城市”和“国家全球旅游示范区创作单位”。九台区通过文化和旅游的互相发酵，形成自己独特的旅游文化，满足了群众日益增长的文化和精神需求。

③ 通过对动态直流干扰的管地电位及动态交流干扰的交流干扰电压进行快速傅里叶变换分析，能够有效的统计出干扰周期分布特征，对于实验室模拟实验的关键参数选取提供依据。

[1] 游盈萱,陆哲睿,王文玲. 基于快速傅里叶变换的可见光室内定位技术的研究[J]. 大学物理，2020(6):68-73.

[2] 周雪松,孟金,姚蔚. 一种基于快速傅里叶变换的多普勒天气雷达弱杂波识别方法[J]. 海洋气象学报，2019(4):43-51.

[3] 刘政委,卓增泗,王伟,等. 基于快速傅里叶变换的燃烧动态监测方法研究[J]. 热力透平，2017(2):127-131.

[4] 刘瑶,谭松玲,邢琳琳,等. 北京埋地燃气管道地铁杂散电流干扰影响现场检测及规律分析[J]. 腐蚀科学与防护技术，2019(4):429-435.

[5] 朱祥剑,杜艳霞,覃慧敏,等. 地铁杂散电流干扰下埋地管道管地电位动态波动规律[J]. 腐蚀与防护，2019(12):878-885.

[6] 刘杰,杜艳霞,覃慧敏,等. 地铁杂散电流对埋地管道的干扰规律[J]. 腐蚀与防护，2019(1):43-47.

[7] 董亮,姚知林,葛彩刚,等. 地铁杂散电流干扰下管地电位波动特征的傅里叶分析[J]. 表面技术，2021(2):294-303.

[8] 肖嵩,姜子涛,童清福,等. 轨道交通杂散电流对武汉燃气管道干扰的波动规律[J]. 腐蚀与防护，2020(12):37-43.

[9] 李伟,杜艳霞,姜子涛,等. 电气化铁路对埋地管道交流干扰的研究进展[J]. 中国腐蚀与防护学报，2016(5):381-386.

[10] 李兴锋,刘舒娴. 电气化铁路对埋地天然气管道交流干扰电压的影响[J]. 石化技术，2019(7):64-66.

[11] 周宇,秦朝葵,陈志光. 轨道交通动态杂散电流干扰及傅里叶分析[J]. 煤气与热力，2013(2):A28-A32.

[12] 程彤,付山林,齐永明,等. 电气化铁路对埋地钢质燃气管道的交流干扰研究[J]. 管道技术与设备，2012 (4):37-39.