基于改进差分进化算法的电力系统经济调度研究

李安燚 ,李晓军 ,田家辉 ,王心蕊 ,崔童飞

(1.国网河北省电力有限公司电力科学研究院,河北 石家庄 050021;2.国网河北省电力有限公司经济技术研究院,河北 石家庄 050021)

0 引言

电力系统经济调度(Economic Dispatch,ED)是电力系统运行与规划中一类重要的优化问题,对电力系统的安全、经济运行具有重要影响。在目前“碳达峰、碳中和”战略背景下,通过经济调度获得的最优调度方案对于电力系统的节能减排具有重要意义。传统经济调度的发电成本函数是一个可微的二次方程,当计及阀点效应、爬坡约束、网络损失、禁止区间等实际问题时,其目标函数将变得非凸、非线性,传统求解方法将不再适用。如线性规划法、二次规划算法、动态规划算法,初始值选择对结果有很大影响,极易陷入局部最优。拉格朗日松弛算法应用于大规模电力系统计算时,可能会导致计算结果振荡。

为克服传统数学求解方法的局限性,国内外学者将目光投向了遗传优化算法,如粒子群算法、差分进化算法、深度学习[1-2]等。以种群进化机制为理论基础,这就导致其控制参数、交叉变异、选择等过程对结果有较大影响。特别是经典差分进化算法,虽然具有控制参数少的优点,但最终计算结果的质量对控制参数的设置非常敏感。若设置种群个体较少,且生成新一代个体的适应值比原种群个体适应值差,就会导致个体难以更新,收敛不到极值点。因此,许多学者将多种智能算法进行结合改进,以提升全局优化能力。Niknam T提出了一种模糊自适应粒子群算法(A Fuzzy Adaptive PSO with Nelder-Mead,FAPSONM),通过引入Nelder-Mead算法,进行局部搜索,提高FAPSO算法性能[1]。Elsayed提出了改进随机漂移粒子群算法(Improved Random Drift Particle Swarm Optimization,IRDPSO)[3],通过在速度更新方程中,增加交叉操作和贪婪选择过程,将粒子的平均最佳位置替换为每个粒子个体最优位置,提升算法进化能力。AS Reddy提出了混合蛙跳差分进化算法(A Hybrid Shuffled Differential Evolution,SDE)[4],该算法结合了蛙跳算法和差分进化算法的优点,通过引入一种新的差分变异算子,从而有效求解大规模非凸经济调度问题。上面所提及的这些算法,虽然对经典粒子群算法、差分进化算法的局限性进行了改进,但是改进后的算法用于求解计及阀点效应的经济调度问题时,求解出的结果离散程度较大,鲁棒性较差。

本文从差分进化算法入手,提出了一种参数动态调整策略,通过引入混沌初始化操作,实现计算全过程算法性能提升,改善差分进化算法易陷入局部最优、求解质量不高的问题。将改进后的算法应用于求解计及阀点效应的经济调度问题,通过算例仿真,验证所提出改进方法的可行性,并与其他方法进行对比分析,突显改进算法优化效果。

1 计及阀点效应经济调度问题数学模型

1.1 经济调度目标函数

本文研究的是火力为单一能源发电的静态电力系统经济调度问题,以系统内所有发电机组发电成本最低为目标,可用二次函数式(1)来表示总发电成本[5]

式中:N为电力系统中发电机总台数;P i为发电机组i的有功出力,ɑi,b i,c i为发电机组的发电成本系数。

由于阀点效应,发电机组的运行成本特性曲线是非凸不连续的,为模拟这一现象,即在式(1)中加一项正弦函数绝对值,可得计及阀点效应的经济调度问题目标函数[6]为

式中:e i,f i为发电机组阀点效应(VPE)系数;为发电机组i的有功出力下限。

1.2 约束条件

经济调度问题的约束条件包括等式约束和不等式约束,等式约束为功率平衡约束

式中:PD为电力系统中总负荷需求;PLOSS为电力系统中总网络传输损失。

通过B系数法计算[6]表示为

式中:B ij、B0i、B00为网损系数;P j为机组j的有功出力。不等式约束包括发电机组有功出力上下限约束、发电机组禁止区间约束

由于在实际系统中,火电机组不能瞬时改变其输出功率,考虑其爬坡约束为

式中:P i0为机组上一单位间隔的输出功率;UR i、DR i分别为机组的爬坡上下限。

将式(5)和(7)进行整理合并得

1.3 约束条件处理

本文采用根据每台机组有功出力的占比来分摊多余有功出力,从而完成机组有功出力的修正,满足不等式约束条件,修正过程流程示意如图1所示。

图1 机组有功出力修正过程流程示意

步骤1:检查每台机组有功出力P i是否满足不等式约束条件式(8),按照式(9)进行修正

步骤2:将当前迭代次数所有机组有功出力之和与系统负荷需求做差得Δ。若|Δ|＞0,则进行步骤3,否则,进行步骤4。

步骤3:通过式(10)对P i进行修正,以满足等式约束条件。

步骤4:对修正后的P i进行检查,若仍存在机组有功出力越限的情况,返回步骤1。

当考虑网络传输损失时,等式约束将很难满足,本文采用惩罚函数的方法处理等式约束[7],即在目标函数中加上惩罚项式中:σ为惩罚因子,在可行域内引导搜索进程,便于快速寻找到可行解,通常设置成一个很大的正值。

2 改进差分进化算法

2.1 标准差分进化算法

差分进化算法由R.Storn和K.V.Price于1995年首次提出[8-9],是一种基于种群差异的启发式并行搜索算法。与其他遗传算法不同的是,DE算法利用种群中个体的差分向量对个体进行扰动,完成个体变异。通过差分变异操作,可以有效利用群体分布特性,提高算法整体寻优能力,弥补其他遗传算法在变异方式中存在的不足[10]。DE算法主要步骤包括种群初始化、变异、交叉以及选择,如图2所示。

图2 差分进化算法主要步骤

对于所优化的问题

DE算法具体流程如下:

(1)初始化种群。按照式(14)随机选取初始值

(2)变异操作。通过在种群中随机选取2个不同个体,对其向量差进行缩放后,与待变异个体进行向量合成,完成突变

式中:x j1,x j2,x j3为从当前种群随机挑选的3个不同个体;F为缩放因子,决定搜索的步长和速度,取值范围为[0,1]。

(3)交叉操作。将基准向量与变异向量进行交叉操作,二项式交叉算子计算为

式中:randi为区间[0,1]内均匀分布的随机数;i n为区间[1,n]内均匀分布随机数;CR为交叉概率,决定着变异前后遗传信息所占权重,取值范围为[0,1]。

(4)选择操作。DE 算法采用贪婪选择机制,可以保证种群始终向着全局最优的方向进化

DE算法具有控制参数少、收敛速度快、求解非线性问题可靠性高等优点,已广泛应用于求解各类问题。然而,DE 算法控制参数选择压力大,算法性能对控制参数的依赖性高,种群个体容易陷入早熟收敛、局部最优、搜索停滞等问题,在应用求解过程中具有一定的局限性。

2.2 混沌初始化操作

标准DE 算法采用随机初始化,为获取分布更加均匀的初始种群,改进后DE 算法(Improved Differential Evolution)引入混沌操作,提升初始种群质量,提高搜索到全局最优解的几率。所采用的一维混沌自映射表达式为

式中:x n为混沌变量,其混沌幅度为[-1,1],仿真计算中设置为区间[0,1]中的随机值。完成数次混沌迭代后,初始化种群将遍历整个解空间。混沌初始化过程如图3所示。

图3 混沌初始化种群步骤

2.3 控制参数动态调整

在经典DE 算法中,缩放因子F和交叉概率CR为一恒定值,适当动态调整控制参数,可以加快DE算法的收敛速度,改善算法性能,降低陷入局部最优的风险。缩放因子F影响着算法搜索的步长和速度,交叉概率CR在变异过程中决定着差分向量的权重。在进化过程中若将缩放因子F设置为递减变化,则有助于初期在解空间范围内高效搜索,后期进行局部重点搜索;若将交叉概率CR设置为递增变化,则可以保证种群初期多样性,增强算法收敛性能。一般改进DE 算法,将2个控制参数设置为简单的线性变化,记作IDE-1

式中:Fmax和Fmin分别为缩放因子F的最大值和最小值;tmax为所设置的最大迭代次数;t为当前迭代次数;CRmax和CRmin分别为交叉概率CR的最大值和最小值。由于线性变化形式过于单一,在寻优初期全局搜索能力强大,但中后期难以满足局部搜索的要求,收敛精度不高,寻优速度较慢,难以适用于对求解精度要求较高的问题。基于此,本文提出了一种动态调整控制参数方案。方案IDE-2将控制参数由线性变化改进为指数形式的非线性变化为

将IDE-1和IDE-2控制参数的变化趋势绘制在图4和图5中。

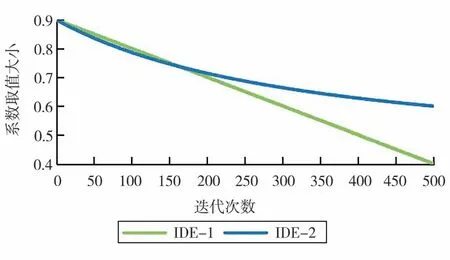
图4 两种方案缩放因子变化趋势

图5 三种方案交叉概率变化趋势

由图4可以看出,2种方案缩放因子均为下降趋势,其中IDE-1为线性递减,IDE-2为非线性递减,且不能取到所设定的边界值。在图5中,三种方案交叉概率均为上升趋势,IDE-1为简单线性递增,IDE-2为非线性递增。两种方案采用不同的函数模型,将在第4节中对此两种方案分别进行经济调度问题的算例仿真分析。

2.4 惩罚因子

惩罚因子的选取对算法的收敛性能有着重要影响,因此,罚函数方法有着一定的局限性,如难以选择合适的惩罚因子,在某些特定条件下表现不佳等。一般情况下,惩罚因子通常设置为一个很大的定值,以起到足够的惩罚作用。本文结合算例规模,将惩罚因子σ按照式(23)进行动态调整

3 算例仿真

在本节将对IDE-1、IDE-2 2种方案分别在13机组、40机组算例中进行计及阀点效应经济调度问题的仿真计算,并与改进前DE 算法进行对比分析。算例1为13机组标准系统,负荷需求为1 800 MW,考虑了阀点效应、网络损失以及禁止区间约束。算例2 为40 机组标准系统的仿真。所用程序通过C++程序编写,在Visual Studio 2012中进行测试,独立运行计算20次,所用计算机配置为Intel(R)Core(TM)i7 CPU (2.80 GHz),8 GB RAM。

3.1 参数设置

虽然DE 算法具有控制参数少的优点,但是这些控制参数对算法性能有较大的影响。通常参数的范围设置需要结合实际问题,经过反复测试得出。DE算法的性能表现取决于3个控制参数,在上一节中,对影响DE算法性能的缩放因子F、交叉概率CR,进行了阐述与改进。种群规模的大小要结合系统规模进行设置,种群设置过小,容易陷入局部最优,种群设置过大,计算时间较长。经过多次仿真测试,具体参数设置见表1。

表1 算例参数设置

3.2 13机组算例

13机组算例采用文献[11]中的标准发电成本参数,计及阀点效应影响,考虑网络传输损失的影响,所采用的网损计算B 系数[12],系统负荷需求为1 800 MW。表2中将方法IDE-1和IDE-2所求的最优结果与其他方法进行对比。

表2 13机组系统计及网损计算结果对比 美元·h-1

由表2可以直观看出,与其他方法相比,采用改进后的DE 算法得到的发电成本低于其他方法。对比IDE-1和IDE-2,采用非线性变化的动态参数调整策略,与单一线性变化相比,所得结果更加理想,且算法鲁棒性得到提升。独立运行20次计算结果分布箱型图见图6。

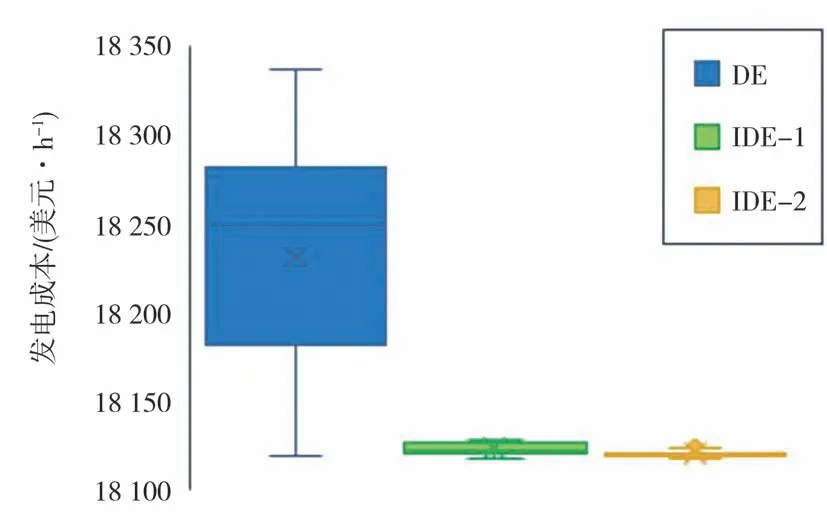
图6 改进前后结果分布对比箱型图(13机组算例)

图6中对比了DE算法改进前后的20次独立计算结果分布,改进前计算所得标准差为65.42美元/h,结果分布范围较大,且平均发电成本较高。经过改进后,平均发电成本减少109.18美元/h,结果鲁棒性得到明显提升,标准差仅为1.93美元/h,说明算法改进有效。对比方法IDE-1与IDE-2,采用非线性动态参数调整策略可以得到更低的平均发电成本,且结果波动范围较小。

3.3 40机组算例

在40机组系统进行仿真测试,所采用计算数据参考文献[16]。在此算例中,系统负荷需求为10 500 MW,计及阀点效应的影响。在表3中,对采用不同方法所得计算结果进行对比。

表3 40机组系统计算结果对比 美元·h-1

在表3中将改进前后DE 算法与其他方法计算结果进行对比,可以明显看出,在最小、平均、最大成本DE算法有明显的优越性,且标准差更小。其中,方法DEPSO、ST-IRDPSO、CBA、CCDE、MCSA 虽然可以得到较为理想的结果,但标准差较大,鲁棒性较差。方法HAAA 虽然标准差小,但所需迭代次数较多。20次独立计算结果分布箱型图见图7。

图7 改进前后结果分布对比箱型图(40机组算例)

由图7可以看出,对比改进前后DE 算法,在20次独立计算中,DE 算法控制参数选取定值时,存在一个异常值,且其余解分布范围较大。当控制参数采用简单线性变化时,求解结果更为稳定。当引入混沌操作,将控制参数改为非线性变化时,结果鲁棒性能更好,改进效果明显。

4 结论

本文将差分进化算法应用到求解计及阀点效应经济调度问题的不同算例中,对其进行有效改进,深入挖掘DE算法潜力。首先,对经典差分进化算法进行研究,分析差分进化算法存在易于陷入局部最优、参数设置选取压力大、对离散的优化问题处理不佳等局限性,并对控制参数作用进行重点分析。然后,对DE 算法进行改进,在初始化阶段引入混沌操作,提升初始种群质量,提出了一种基于非线性控制参数动态调整方案。最后,将所提出的IDE算法应用于2个不同规模算例中进行仿真测试。仿真结果显示,在考虑不同约束条件的算例中,与其他方法相比,所提出的改进算法能在求解到最优结果的同时,鲁棒性也更为出色。