考虑时空相关性的风光出力序列生成方法
李 泽,李铁成,严敬汝,陈天英,郭少飞
(国网河北省电力有限公司电力科学研究院,河北 石家庄 050021)
0 引言
随着我国“双碳目标”的提出以及新型电力系统建设进程的不断推进,以风力发电和光伏发电为代表的新能源将在我国能源系统中发挥越来越重要的作用。但是,风力发电和光伏发电受地理位置和气候影响较大,具有不确定性和波动性[1-2],其大规模并网必将给电力系统安全稳定运行带来巨大挑战。
实际上,同一地区的风光能源在出力上存在一定的相关性[3],充分利用能源之间的相关性并形成联合调度,可有效克服风光的不确定性带来的不良影响。目前,关于风光出力的相关性方面已有一些研究。文献[4]基于非参数核密度估计分别构建了静态相关系数估计和动态相关系数估计,针对算例数据分别估计相关参数,最后通过拟合优度检验和合理性验证对比了模型刻画效果,证明了动态相关性模型的合理性及有效性。文献[5]认为单一模型仅能描述局部相关性,很难适应复杂相关性的建模,为此提出了混合藤Copula模型,并通过算例验证了所建模型的有效性。文献[6]运用Spearman相关系数来描述风光之间的出力相关性,再基于神经网络算法和综合场景概率法分别得到风电出力和光伏出力,最终生成4组风电出力和1组光伏出力,通过计算光伏与各组风电出力之间的相关性系数来分析风光相关性对无功优化的影响。文献[1]通过肯德尔秩相关系数反映变量之间的相关性,生成典型风光联合出力场景。文献[2]在考虑风光空间相关性的基础上,提出了考虑风光场站出力时间相关性的建模方法,形成了关于风光多维时空相关性的出力场景。文献[3]基于非参数核密度估计得到各样本的边缘分布函数,随后根据Frank-Copula将样本连接起来得到联合概率分布函数,分时段对分布函数进行采样,并反变换得到风光出力,最后通过K-means聚类得到典型日场景及对应概率。以上文献,有的只使用了一种Copula函数来描述风光相关性,未考虑同一地区的风光在不同时段可能存在不同的相关特性,有的通过聚类等方法来获得风光出力场景,风光出力样本取自于各时段的风光出力相关性模型,这种方法舍弃了风光出力相关性在时间上的连续,且包含了每天风光场站运行环境情况大致相同的假设,不符合实际情况。
本文提出一种考虑时空相关性的风光出力生成方法。首先,基于动态马尔科夫链方法确定相邻时刻功率变化的方向和幅值,以此考虑风光出力的时间相关性。然后,基于非参数核密度估计分别对各时刻原始风光出力进行拟合,得到各时刻风光出力的边缘概率密度函数,并采用Copula函数构建各时刻风光出力的联合概率分布,以保证风光出力的空间相关性。接着,结合以上方法生成具有时空相关性的风光出力序列。最后,通过算例验证了本文所提方法的有效性。
1 风光出力相关性理论
1.1 Copula理论
Copula函数最早在1959年由Sklar提出[7-9],常被用于描述多元随机变量之间的相关性,是一种将各变量的边缘分布函数连接成联合分布函数的函数,设多个随机变量的边缘分布函数为F1(u1)、F2(u2)、…、F n(u n),其联合分布函数为H(u1,u2,…,u n),当F1(u1)、F2(u2)、…、F n(u n)连 续时,存在一个唯一确定的Copula函数C满足
在研究中最常用的Copula函数主要包括两大类[10-12],椭圆Copula函数和阿基米德Copula函数。椭圆Copula 函数包括Gaussian-Copula,t-Copula等,但由于其具有对称的尾部相关性,故无法描述非对称的相关关系。阿基米德Copula函数有着统一的函数表达式,通过调整其中的生成元函数,即可得到不同的阿基米德Copula函数,常见的有Gumbel-Copula,Clayton-Copula,Frank-Copula等。其中,Gumbel-Copula和Clayton-Copula函数分别只对上尾部和下尾部的厚尾特性敏感,而Frank-Copula函数的密度分布呈“U”字形,适合于描述具有对称厚尾结构变量的耦合关系,且分布比较均匀[13]。因此,本文选用Frank-Copula函数来描述风光出力的空间相关性。Frank-Copula函数如下
式中:u、v为随机变量;θ为Frank-Copula函数的相关性系数,且θ≠0,当θ>0时,随机变量间呈正相关关系,当θ<0时,随机变量间呈负相关关系;e为自然常数。
在数学上,常用相关性系数来刻画2个随机变量之间的相关性。本文选用Kendall秩相关系数τ,其表达式为
则Frank-Copula函数的相关性系数θ可根据Kendall秩相关系数τ推算
1.2 马尔科夫链
风光出力序列不仅具有空间相关性,还具有时序相关性,即相邻时刻风光出力在数值大小上呈现一定的规律性[14-15]。而马尔科夫链可通过前面有限个序列确定当前序列的取值,可以很好地描述风光出力的时间相关性。设{X(n),n=0,1,2,…}为状态空间是参数非负的随机过程(状态空间为I),如果{X(n)}满足
则称随机过程{X(n)}为马尔科夫链。式中:P(·|·)为条件概率;k(i n+1|i n)为随机过程{X(n)}的状态转移核。
2 风光出力时空相关性建模
基于常规马尔科夫链方法对风光出力序列采样,只能求出风光出力序列在各状态下的概率分布,无法得到确定的风光出力状态。有研究在这一步采用了马尔可夫转移概率最大化法[16],只选取最大转移概率处的状态进行计算,这从客观上摒弃了非最大转移概率事件发生的可能性,势必导致计算结果有失全面性。
本文提出动态马尔科夫链采样方法,将风光出力变化分为若干种状态,状态转移矩阵随时间而变化,结合各时刻状态转移矩阵和各状态出力变化范围,计算出下一时刻的出力期望值。
通过分析河北省南部电网某地区2个位置相邻风电场和光伏电站的实际出力序列,发现在有效观测区间内,风电场出力Pw和光伏电站出力Ps在t+1时刻的出力状态均与其在t时刻的状态不同,即Pw,t≠Pw,t+1,Ps,t≠Ps,t+1。因此,假设t时刻风光出力序列为P t,则有P t={Pw,t,Ps,t},对于t+1时刻,P t有4种可能的转移状态,分别为风光出力均增大、风出力增大光出力减小、风出力减小光出力增大和风光出力均减小,将其发生概率分别设为k t_t+1,i(i=1,2,3,4)。
对于t时刻到t+1时刻的风光出力状态转移矩阵,即K t_t+1有
以t时刻出力条件下,t+1时刻风光出力均增大的情况为例。基于风光出力序列样本,计算t时刻到下一时刻风光同时增加的情况频数m t_t+1,1,t时刻总的样本数量记为M t_t+1,1,则有
同时,计算风光出力增大比例的最大值和最小值,分别记为nw,1,max|t_t+1、nw,1,min|t_t+1和ns,1,max|t_t+1、ns,1,min|t_t+1。为了简化计算,在此将各状态下风光各自出力变化情况看作线性变化,则t+1时刻风电在风光出力均增大时的出力期望值为
重复上述步骤得到t时刻下4个状态期望值,再通过加权计算可得t+1时刻的风光出力期望值。
3 风光出力序列生成步骤
风光出力序列生成步骤如下:
(1)生成2个在(0,1)上服从均匀分布的随机数作为风光出力序列初始值,分别记作Pw,1、Ps,1;
(2)基于风光出力序列样本计算从当前时刻到下一时刻的转移概率矩阵K t_t+1;
(3)分别计算下一时刻各状态出力变化比例的最大值和最小值,结合式(8)、式(9)计算各状态出力期望值其中j表示所属转移状态,j=1,2,3,4;
(4)对步骤(3)所得各状态出力期望值进行加权计算得下一时刻风光出力期望值,权重为各状态对应的转移概率k t_t+1,j,则有
(5)根据式(3)、式(4)计算t+1时刻风光出力序列得到对应Frank-Copula函数的参数θt+1;
(6)计算参数为θt+1的Frank-Copula函数C(u,v)在附近的解,并取欧氏距离最小者作为t+1时刻风光出力计算值Pw,t+1和Ps,t+1;
(7)重复步骤(2)—(6),直至风光出力序列生成数满足要求。
4 算例分析
4.1 样本数据
以河北省南部电网某地区2个位置临近的风电场和光伏电站7—8月连续30 d的出力数据为样本。表1为根据样本求得的风光出力的均值、中位数及方差。风电场容量为150 MW,光伏电站容量为200 MW,实际计算时均采用风光出力的标幺值,统计区间为每天06:00—18:00时间段,数据采样间隔为5 min,风电场出力记为Pw,光伏电站出力记为Ps。图1为原始数据对应的风光出力序列散点示意。

表1 风光出力统计特征

图1 原始风光出力散点示意
4.2 Frank-Copula模型参数估计
采用非参数核密度估计法确定风光出力的边缘概率分布函数F(Pw)和F(Ps)。对某一变量X={X i},i=1,2,…,n,其概率密度函数的核估计为[17-18]
式中:n为样本数量;K(x)为核函数,本文取高斯函数;h为带宽系数,其值选择将影响对X i的拟合准确度,本文根据最优带宽经验公式进行求解[19],如式(13)所示。对进行积分即可得到风光出力的边缘概率分布。
图2给出了Pw和Ps经验分布曲线和核分布估计曲线。由图2可看出,采用非参数核分布估计得到的样本拟合结果,可以很好地描述风光出力的数据特征,且光滑度更好。
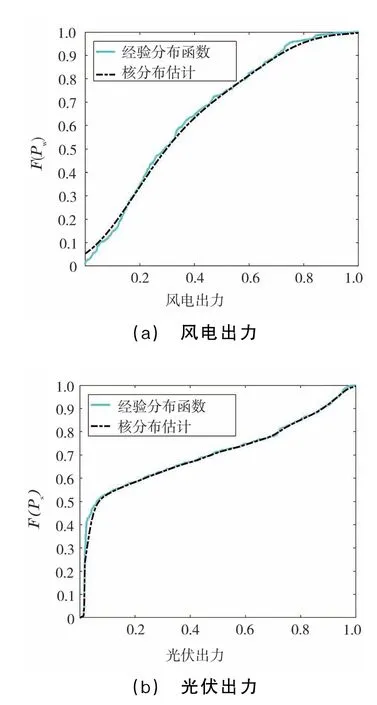
图2 风光出力分布曲线对比
基于非参数核分布估计法对每个时刻的风光出力数据进行拟合,再根据式(3)、式(4)分别计算风、光同一时刻的相关性系数,最终由式(2)得到相应的Frank-Copula模型。以第84个时刻为例,表2给出了该时刻风、光出力概率密度函数的带宽系数及Frank-Copula模型的相关性系数,图3(a)为Frank-Copula函数拟合的风光出力密度函数,图3(b)为拟合的风光出力分布函数。


图3 第84个时刻拟合值的概率密度及分布情况

表2 第84个时刻的带宽系数及相关性系数
4.3 方法验证
根据第3节步骤生成风光出力序列,图4为按照本文方法拟合得到的风光出力时序图。将风光出力的原始数据分别按时刻划分求取平均值,可得风光原始出力的整体变化情况,如图5所示。在风光原始数据中,分别寻找与拟合风光出力之间欧氏距离最小的风电和光伏出力序列,结果为第27天风光出力均最接近拟合结果,此时风电出力实际值与拟合值之间欧氏距离为1.094 4,光伏出力的欧氏距离为1.429 8,第27天风光实际出力情况如图6所示。

图4 风光出力序列拟合情况

图5 风光原始出力情况

图6 第27天风光出力情况
对比图4-6可以看出,拟合结果基本保留了原始样本的数据特征,同时也具有一定的随机性。在06:00—10:00,拟合结果中光伏出力逐渐增大,风电出力则在波动中逐步下降,这与原始样本的出力变化趋势相符。而这段时期光伏拟合出力较原始出力增大更快,这是由于原始样本中存在部分数据点前期光伏出力为0,导致通过平均求得的光伏原始出力变化率减小。
由图6可以看出,原始样本中存在光伏起始增大较快的情况,故本文方法较好地兼顾了样本整体与个体的数据特征。在10:00—12:00,拟合结果中光伏出力先是下降,然后维持在较大出力位置,与原始样本中光伏出力持续在最大出力附近波动不同,这是因为光伏电站在正常运行时,有时会因白云遮挡阳光导致出力下降,而原始样本出力因为求和平均的算法使得该数据特征被抹去,拟合结果中的光伏出力就是将这种随机性体现了出来。在12:00—18:00,拟合结果中光伏出力逐渐下降,风电出力随之升高,与原始样本的出力变化情况一致。整体来看,拟合结果中的风电出力较原始样本平均出力波动范围要大,更符合实际运行情况。
为进一步验证本文方法的实用性,以天为单位对原始样本进行分类,形成代表风光出力大、中、小的3种运行情况,并分别将其所包含数据定义为第1组、第2组和第3组,各类运行情况相关信息如表3所示,采用第3节方法分别对3组数据进行仿真模拟,模拟结果的统计数据如表4所示。

表3 风光出力运行情况分类结果
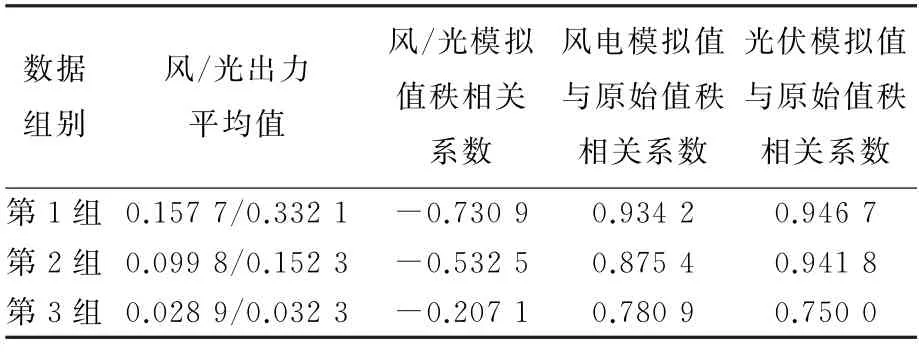
表4 各类风光出力运行情况模拟结果
统计数据显示,根据本文所提方法得到的模拟结果很好的保持了样本数据的均值特征,误差均不超过7%。模拟结果中,风光出力最大时其秩相关系数为负且幅值也最大,代表其负相关属性较强;当风光出力最小时,负相关属性最弱,这与原始数据的特征一致,说明本文方法很好地保持了风光出力的空间相关性。分别计算模拟结果中风光出力与原始数据中风光出力的秩相关系数,可以发现其正相关性属性较强,最大为0.946 7,最小为0.750 0,说明本文方法能够模拟风光出力各自的变化趋势,较好地保留了风光出力的时间相关性。从表4数据进一步可以看出,随着出力水平的降低,风光模拟结果与原始数据的秩相关系数也在逐渐减小。其原因:一是样本数量逐步减少,随之带来的误差增大;二是随着风光出力水平下降,其出力的随机性和波动性进一步增强,引起模型计算的偏差增大,导致变量之间的相关性降低。
4.4 适应性分析
提取风电场和光伏电站第31天的实际出力数据,并将其与拟合结果进行对比,如图7、图8 所示。由图7和图8可以看出,在06:00—10:00,风光实际出力与拟合结果吻合度较高。随后风电实际出力骤升,超过拟合结果预测值,此时光伏实际出力则持续波动,始终在拟合结果附近震荡。该情况持续到15:00左右,风电实际出力突然大幅下降跌至拟合结果预测值以下,而光伏实际出力则恢复与拟合结果较高的吻合水平。通过查询天气数据,当天地区发布大风黄色预警。由此可以推测,10:00—15:00的数据波动为短时极端强对流天气所致,而此类随机影响难以从风光历史出力数据中提取并分析[20-21],因此导致部分时段预测值误差较大。表5给出了风光预测出力水平和第31天实际值的对比情况。

图7 第31天风电实际出力与拟合结果对比

图8 第31天光伏实际出力与拟合结果对比

表5 风光出力情况对比
为了更直观对比,将观测周期按照该文分析结果划分为3个阶段。通过表5比较可知,全周期内,风光预测误差分别为8.13%和5.26%,在可接受范围内。其中,06:00—10:00 以及15:00—18:00风光预测平均值与实际平均值相差极小,误差均在5%以下,体现了本文方法在天气稳定情况下较好的准确性。10:00—15:00,预测出现较大误差,且风电出力误差超过25%。一方面,证明了短时极端天气变化难以预测,模型在该问题上仍有待完善,另一方面,某些极端天气变化对风电的影响要远大于对光伏的影响,这在今后的研究中应着重考虑。相关性方面,以光伏为例,全周期秩相关系数为0.757 6,证明模型较好地模拟了光伏出力变化趋势。其中,06:00—10:00、15:00—18:00 模拟结果尤为出色,秩相关系数均在0.900 0以上。
5 结论
本文从风光出力序列的时间相关性和空间相关性2个角度出发,基于Frank-Copula函数和动态马尔科夫链采样,建立了考虑时空相关性的风光出力模型,提出了一种新的风光出力序列生成方法。通过算例验证得出以下结论。
(1)与常规采样方法抹去了变量的时序特征不同,基于本文提出的动态马尔科夫链进行采样,结果既能反映变量的概率分布,又能够维持变量的时序特征,再现变量自身的时间相关性。
(2)Frank-Copula函数能够模拟变量间的相关性,尤其是对于具有负相关性的风光出力模型,Frank-Copula函数能够很好地展示地理位置和地形环境带来的空间相关性。
(3)本文方法在天气稳定情况下能够较好地模拟风光出力的变化趋势。短时极端强对流天气是风光出力预测的一个重要影响因素,尤其对风电出力的影响往往更大,这在今后的研究中仍有待完善。相关性风光出力模拟能够为电力系统经济调度及新能源规划提供数据基础,把模拟得到的计及时空相关性的风光出力序列应用到新能源高渗透率电力系统中以提升电能质量和优化运行,将是下一步的研究工作。

