基于虚拟阻抗的多逆变器功率分配控制研究

崔童飞,程子玮,董靓媛,张 蕊,戎士洋

(国网河北省电力有限公司电力科学研究院,河北 石家庄 050021)

0 引言

随着新能源发电技术快速发展,风电、光伏成为新增电源主力军[1]。截至2021年年底,全国新能源装机容量达到6.34亿千瓦,风电利用率达到96.9%,光伏发电利用率达到97.8%。推进能源低碳转型,实现能源深度脱碳,构建新型电力系统,成为当下发展的重心和热点[2-4]。为加快新能源消纳,在同一时空往往存在多个电源同时并联情况,必然会涉及多逆变器并联运行的控制问题。

实际中,由于各电源的时空位置差异,逆变器到并网点的线路阻抗可能不同,将产生不同程度的压降,进而造成多逆变器间的功率耦合和分配不均,可能成为威胁电网安全稳定的隐患[5-7]。

针对多逆变器间功率耦合和分配不均问题,国内外诸多学者展开了深入研究。文献[8]提出一种基于虚拟电阻的均流改进方法,适用于等容量逆变器系统的功率解耦,但当逆变器系统容量不等时,解耦效果不佳;文献[9]提出一种变下垂系数步长的改进策略,可以降低多逆变器间的功率耦合,但功率解耦效果一般,而且系统整体鲁棒性较弱;文献[10]提出一种基于虚拟同步发电机的改进策略,在下垂环路中添加了微分环节和惯量因子,降低了功率解耦程度,但控制算法过于复杂。

本文针对多逆变器并联运行时存在的功率耦合和分配不均问题,提出了一种基于虚拟阻抗的改进策略,弱化线路阻抗差异对功率分配的影响,大大提高了功率分配精度。最后通过仿真验证了该方法的合理性和可行性。

1 多逆变器的功率传输特性分析

含m个逆变器的并联系统等效模型如图1所示。各个逆变器均采用下垂控制[11-12]算法,其特点是通过模拟同步发电机的下垂特性来进行一次调频和调压,彼此之间无需通信线交互,经济性好,拓展性强[13-14]。

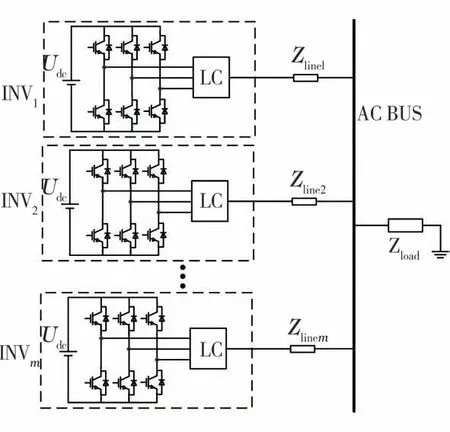
图1 多逆变器并联系统等效模型

1.1 并联逆变器的功率均分机理

为简化分析,以2台逆变器并联为例进行探究,如图2所示。

图2 2台逆变器并联等效模型

图中,E i∠φi(i=1,2)为逆变器内部等效端电压(∠为电压幅值和相角的分隔符);Ioi(i=1,2)为逆变器输出电流;Zoi(i=1,2)为逆变器内部等效阻抗;Zlinei(i=1,2)为逆变器到并网点的线路阻抗;Zload为交流母线上的公共负载;Upcc∠θ为并网点电压;UL∠0为负载Zload的端电压;Z i∠βi为逆变器的等效阻抗,如式(1)所示。

逆变器输出的有功、无功功率,其取值如式(2)和式(3)所示。

式中:P i(i=1,2)为逆变器输出的有功功率;Q i(i=1,2)为逆变器输出的无功功率。

通常,逆变器端电压的相位角极小,往往近似等效成sinφi=φi,cosφi=1,因此,式(2)和式(3)可化简为式(4)和式(5)。

当线路电压较低时,线路中的感性成分Xline远小于阻性成分Rline,即βi=90°,因此,式(4)和式(5)可化简为式(6)和式(7)。

由式(6)、式(7)可知,有功功率P i与逆变器端电压的相位角φi相关,因此,可通过调整相位角φi实现对有功功率P i的控制;无功功率Q i与逆变器端电压幅值E i和负载端电压UL相关,因此可通过调整E i与UL实现对无功功率Q i的控制。

1.2 线路阻抗对功率分配的影响机理

当多个逆变器并联运行时,各逆变器的工作频率相同,因此与频率相关的有功功率能够按照预设完成均分[7],由于时空位置差异,各逆变器到公共母线的线路阻抗Z i往往不相等,由式(7)可知,其输出的无功功率Q i也必然不等。因此,对式(6)所描述的逆变器的端电压E i与线路阻抗Z i的关系,进一步推导得

根据式(8)所描述的逆变器端电压E i和线路阻抗Z i的关系式,绘出包含下垂系数和线路阻抗个变量的无功-电压下垂特性曲线,如图3所示。

图3 并联逆变器的无功-电压下垂特性曲线

图3中,M1、M2为下垂系数大小不同的2条下垂曲线,其中,M1的下垂系数小于M2;INV1、INV2为线路阻抗大小不同的2个并联逆变器,其中,INV1所对应的线路阻抗大于INV2所对应的。由图3可知,逆变器INV1端电压E1大于逆变器INV2端电压E2,但其无功功率Q1却低于Q2。通过对比分析下垂系数为M1时的A、B点和下垂系数为M2时的C、D点的功率差额发现,下垂系数增大时,2 个逆变器的无功功率差额会下降,但同时会引起电压严重跌落甚至越过规定限额,降低系统的运行稳定性,因此仅通过调整下垂系数[7]来实现无功均分的方法尚存在不足和局限,需进一步改进控制策略,在保证系统稳定运行的前提下,实现无功功率有效均分。

2 基于虚拟阻抗的改进策略设计

为解决多逆变器因时空差异导致线路阻抗不一致造成功率耦合的问题,本文提出了一种基于虚拟阻抗的改进策略,重塑逆变器的等效输出阻抗,降低功率耦合程度,使其自动按照预设进行功率分配。

以逆变器输出电压和电感电流为状态变量,建立逆变器在三相静止坐标系下的状态空间方程,如式(9)和(10)所示。

式中:u j和i j(j=a、b、c)分别为直流侧逆变后得到的桥臂输出电压和电流,而uoj和ioj(j=a、b、c)分别为经过LC滤波后的逆变器输出电压和输出电流,iLj(j=a、b、c)表示流经电感的电流。

为方便建模,通常把其变换到dq同步坐标系下,这时各交流分量变为直流分量,由三相变为两相,控制器设计大大简化。逆变器的状态空间方程如式(11)和式(12)所示。

式中:iLd、iLq分别为电感电流在dq轴上的分量;iod、ioq分别为逆变器输出电流在dq轴上的分量;uod、uoq分别为逆变器输出电压在dq轴上的分量。

通过解耦计算,得到dq坐标系下含有电压、电流的双闭环控制框图,如图4所示。

图4 电压电流双闭环控制框图

参照图4,可推导出电压参考值u*od,q(s)到输出电压uod,q(s)的传递函数,即电压增益传递函数Ggain(s),如式(13)所示;输出电流iod,q(s)到输出电压uod,q(s)的传递函数,即逆变器的等效输出阻抗Zo(s),如式(14)所示。

通过引入虚拟阻抗,尽可能的增强等效阻抗中的感性分量,将输出阻抗设计成基波频率处感性特征明显的参量,完成线路阻抗重塑,实现有功和无功功率的解耦控制,其控制框图如图5所示。

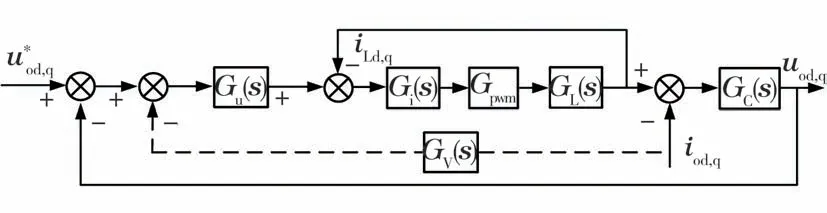
图5 引入虚拟阻抗后的电压电流双环控制框图

引入虚拟感抗后的逆变器等效输出阻抗如式(15)所示。

式中:Gv(s)为引入的虚拟阻抗,Gv(s)=Rv+j Xv。根据式(15)设置不同的虚拟阻抗值(Rv=0.3Ω,Xv=1 m H、3 m H、5 m H、9 m H)可得如图6所示的等效输出阻抗伯德图,参数设置见表1。

表1 系统参数

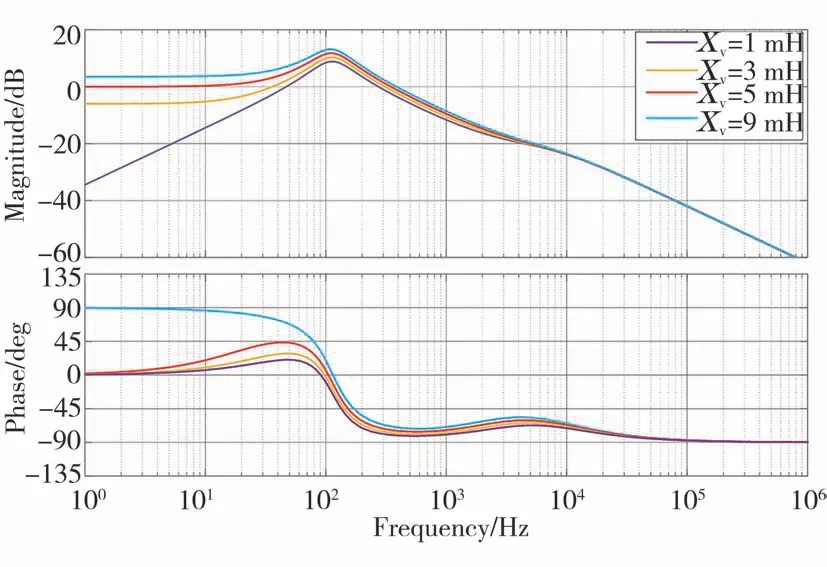
图6 引入虚拟阻抗后的伯德图

由图6可知,引入数值大小不同的虚拟阻抗后,系统的等效输出阻抗呈现出不同的相幅特性。在幅频特性曲线的低频部分,即基波频率50 Hz附近,逆变器等效输出阻抗的增益随虚拟阻抗的增大逐渐上升,近乎为一条平稳的直线;在相频特性曲线的低频部分,随着虚拟阻抗的增大感性特征越来越明显,且带宽也变得更大,有利于并联系统的功率解耦控制,提升功率分配精度,但虚拟阻抗也不宜过大,容易产生较大的压降,降低电能质量。

3 仿真验证

为了验证所提策略的正确性和有效性,在PLECS中搭建了如图7所示的容量比例为1∶1的并联系统模型,2台逆变器为各自的本地负荷供能之外,还共同支撑母线上的负荷,各模块取值和控制参数如表1所示。

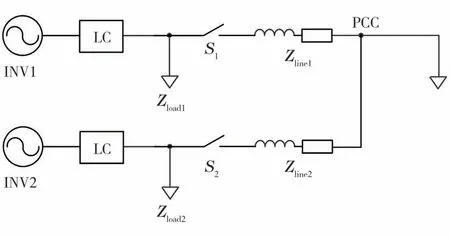
图7 逆变器并联系统拓扑结构

仿真时间总长设置为2 s,在0.5 s之前2台逆变器独立带载运行,0.5 s处投入公共负载。采用传统控制策略时,并联系统的有功功率和无功功率分配状况如图8所示。

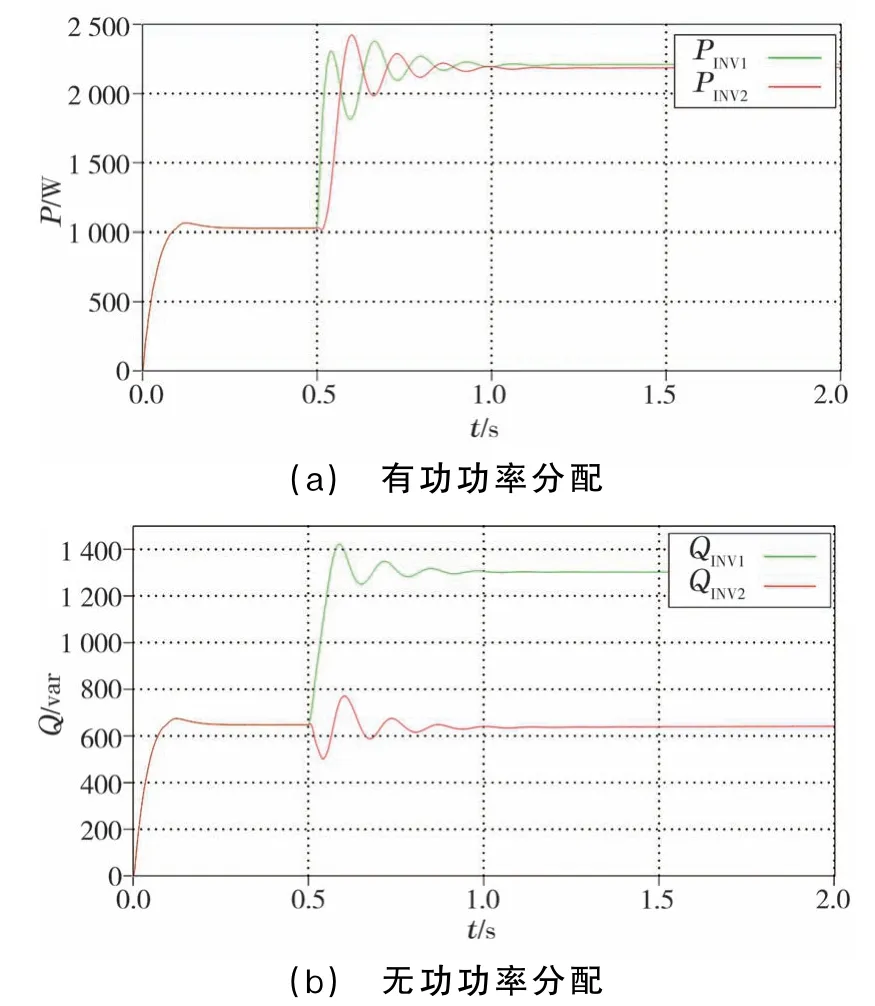
图8 线路阻抗不同时的功率分配状况

由图8可知,0.5 s投入公共负载后,经过0.55 s系统重新进入稳定状态,有功功率受线路阻抗差异影响较小,逆变器1的有功功率为2 230 W,逆变器2的有功功率为2 200 W,基本能够按照预设的1∶1容量配置进行分配;而无功功率的分配受线路阻抗影响出现较大偏差,逆变器1的无功功率为1 300 var,逆变器2的无功功率为630 var,相差一倍左右。

采用本文所提的虚拟阻抗控制策略,并联系统的有功功率和无功功率分配状况如图9所示。

图9 引入虚拟阻抗后的功率分配状况

由图9可知,引入虚拟阻抗后,大大改善了并联系统的功率分配状况,有功功率可以实现准确的功率分配,无功功率差额也由原来的670 var缩小到现在的45 var,无功功率均分精度明显增强,证实了所提策略的有效性。

为进一步验证该方案的适用性,调整局部负载取值,将Zload1,2设置为R=10Ω,L=2.5 m H,公共负载保持不变,其余运行参数与控制参数与上一算例保持一致,采用传统控制策略时,并联系统的有功功率和无功功率分配状况如图10所示。

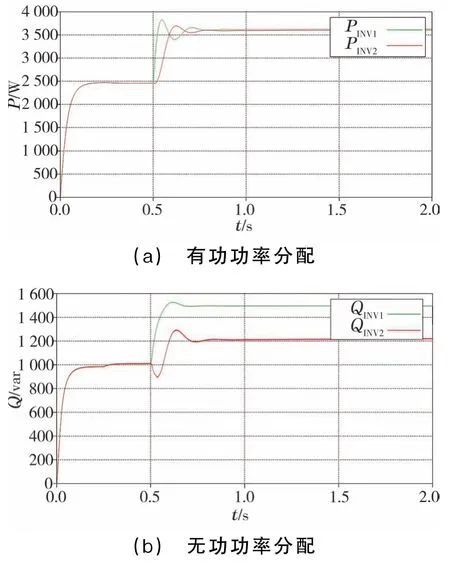
图10 改变局部负载后的功率分配状况

由图10可知,有功功率不受线路阻抗差异影响,在公共负载投入前后都可以实现良好均分;无功功率受线路阻抗差异影响较大,公共负载投入后逆变器1的无功功率为1 510 var,逆变器2的无功功率为1 205 var,功率偏差为305 var。

基于以上验证,引入虚拟阻抗控制环节,观察并联系统的功率分配状况如图11所示。

图11 引入虚拟阻抗后的功率分配状况

由图11可知,引入虚拟阻抗后,逆变器1的无功功率为1 400 var,逆变器2的无功功率1 370 var,功率偏差为30 var,无功功率分配状况明显提升,再次证实了所提虚拟阻抗策略的有效性。

4 结论

针对多逆变器并联系统因线路阻抗差异导致功率耦合和分配不均问题,设计了一种基于虚拟阻抗的改进方法,重塑了逆变器的等效输出阻抗,降低了线路阻抗引起的功率耦合程度,实现了功率的良好分配,所提策略具有重要的工程指导意义。