基于“模型思想”的高中数学立体几何单元复习教学设计

◎ 海南省华侨中学 赵 涛◎ 海南省海口市教育培训院 孙元勋

一、问题的提出

高三复习不是知识的简单重复和再现，而是巩固和加深学生对已学知识的理解，使所学知识系统化、条理化，帮助学生形成知识网络结构。教师通过对学生已学过的知识重新整合与加工，有所创新，激发学生的学习兴趣，促进学生深度参与学习活动，可以提升学生对知识的领悟、内化和升华，从而提高高三复习教学的效率。

高中数学中立体几何内容作为一个重要模块，是培养学生直观想象、逻辑推理等数学核心素养的重要内容载体。主体几何内容知识点多且零散，考查方式题型多样，学生掌握较为困难，尤其是空间向量知识进入高中数学教学之后，学生往往不愿思考，完全依靠向量坐标法来求解，陷入耗时耗力、会而不对的境地。因此，更需要教师站在单元教学的视角下，帮助学生加深对几何图形结构特征及基本图形之间关系的系统认识。

二、“立体几何中的模型思想”单元教学设计

喻平教授认为，从数学单元教学的设计和应用层面分析，数学单元教学主要有“以问题解决过程线索为主题”“以建立个体CPFS结构（个体头脑中内化的数学知识网络）为主题”“以概念生长为主题”和“以数学思想方法解决问题为主题”四种单元教学设计模式。其中“以数学思想方法解决问题为主题”的单元教学按照“确定数学思想方法—围绕方法设计题组—师生共同解决问题—回顾反思总结规律”组织实施。下面根据“以数学思想方法解决问题为主题”的单元教学模式，进行“立体几何中的模型思想”教学设计。

1.情境引入。

引导语：《九章算术·商功》中有这样一段：“斜解立方，得两堑堵。斜解堑堵，其一为阳马，一为鳖臑。阳马居二，鳖臑居一，不易之率也。”

师生活动：请同学朗读，并解释含义。

设计意图：用鳖臑生僻字活跃课堂气氛，吸引学生注意，引入本堂课的主题。

2.解密鳖臑，垂直一线牵。

探究一：问题1：如图1，PA⊥平面ABC，AC⊥BC，四面体P-ABC中有几个直角三角形?你能发现哪些平面互相垂直？为什么？

图1

师生活动：通过师生交流，明确△PAB，△PAC，△ACB，△PCB是直角三角形。

追问1：为什么？你能分别哪个角是直角？如何证明？

设计意图：唤醒记忆，在直角三角形的判定当中，复习线线垂直与线面垂直的相互转换。从△PAB，△PAC是直角三角形的判断中复习直线与平面垂直的判定定理，从线面垂直得到线线垂直；在△PCB是直角三角形的判断中，体会从线线垂直转化至线面垂直，再从线面垂直的定义转化为线线垂直，培养学生逻辑推理能力。

追问2：你能发现哪些平面互相垂直？为什么？

师生活动：引导学生发现平面PAB⊥平面ABC，平面PAC⊥平面ABC，平面PBC⊥平面PAC，在师生交流过程中理解平面与平面垂直判定定理。

设计意图：将线线垂直与线面垂直关系进一步向面面垂直转化，复习平面与平面垂直的判定定理。在探究过程当中，复习三种垂直关系的相互转换，明确线面垂直在三种垂直关系中的核心作用。引入基本图形，给出鳖臑定义，引导学生在研究空间图形的过程中学会思考，提高学生发现和提出问题、分析和解决问题的能力。

3.巧识鳖臑，妙解空间角。

问题2：如图2，在三棱锥P-ABC中，PA⊥底面ABC，AC⊥BC，若PA=AC=BC，M是PB的中点，求AM与平面PBC所成角的正切值。

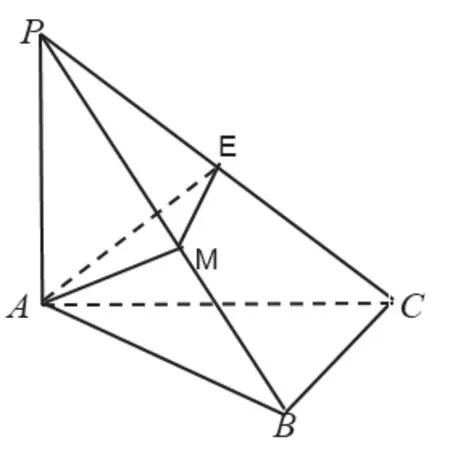
图2

师生活动：问答，学生板演，展示。

设计意图：高三复习过程中，学生容易重视空间向量法，忽视几何法，对线面角的作法不熟悉，答题困难。在鳖臑模型的基础上，附加条件，从证明问题变为求直线与平面成角问题。引导学生复习线面角的作法，复习借助面面垂直的性质定理来作平面的垂线，并从几何法的角度给出解答。

分析：取PC中点E，连接AE，EM，由PA=AC，则AE⊥PC，由平面PBC⊥平面PAC，且平面PBC∩平面PAC=PC，则AE⊥平面PBC，则∠AME为AM与平面PBC所成角。易得t。

探究二：问题3：如图3，PA⊥平面ABC，AC⊥BC，各个面形成几个二面角？分别是哪些？你会求吗？

图3

师生活动：在交流的过程中引导学生找出图3中6个二面角的平面角。

设计意图：复习二面角的概念，并根据二面角的平面角定义，明确作出二面角的平面角的方法——定义法、垂面法和垂线法，如上图4所示。

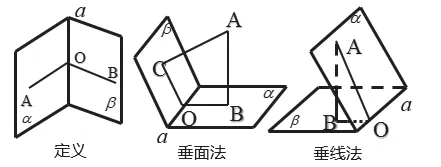
图4

问题4：如图5，PA⊥平面ABC，BC⊥AC，若PA=AC=BC，试求二面角C-PB-A的大小。

图5

分析：设PA=AC=BC=1，取PC中点E，连接AE，由PA=AC，则AE⊥PC，由平面PBC⊥平面PAC，且平面PBC∩平面PAC=PC，则AE⊥平面PBC，作EF⊥PB，则PB⊥平面AEF，连结AF，PB⊥AF，则∠AFE为二面角A-BP-C的平面角，因为△PFE∽△PCB，易得，△AEF中，，则二面角的大小为。

设计意图：复习二面角的平面角的作法，体会立体几何问题平面化的思想。

问题5：如图6，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB交PB于点F。

图6

（1）求证：PB⊥平面EFD；

（2）求二面角C-PB-D的大小。

师生活动：问答，请学生说出想法。

设计意图：基本图形识别，活学活用，立体几何问题要学会识图，能从拆分角度分析识别基本图形。

4.玩转鳖臑，补形出体积。

问题6：如图7，在三棱锥P-ABC中，PA⊥底面ABC，AC⊥BC，若PA=AC=BC=1，求该三棱锥的外接球的体积。

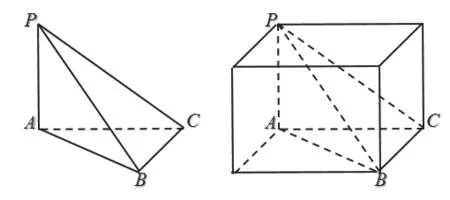
图7

分析：由于PA、AC、BC两两垂直，可将三棱锥P-ABC补形成正方体。三棱锥P-ABC的外接球即为正方体的外接球。PB即为正方体对角线，也是外接球的直径，体积为π。

设计意图：关注鳖臑中的两两垂直特点，从补形的角度来分析基本图形。

5.再析鳖臑，妙解空间角。

问题7：如图8，在三棱锥P-ABC中，侧棱PA⊥底面ABC，AC⊥BC，若PA=AC=BC，M是PB的中点。

图8

（1）求AM与平面PBC所成角的正弦值；

（2）求二面角C-PB-A的大小。

分析：立体几何问题的解决可以选取几何法也可以选取空间向量坐标法，如果能将鳖臑模型识别出来，从正方体的角度来分析，平面CPB和平面APB的法向量是可以直接给出的，有利于明确解题方向，提高解题速度。

设计意图：体会几何法与向量坐标法的关系，认识到深刻理解空间几何体中的点线面的位置关系对于解决立体几何问题的重要性，提高向量坐标法解题运算的准确性和速度。

6.回扣主题。

“斜解立方，得两堑堵。斜解堑堵，其一为阳马，一为鳖臑。阳马居二，鳖臑居一，不易之率也。”

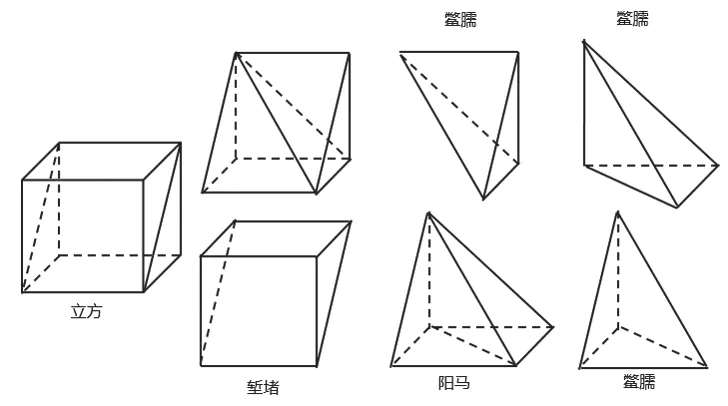
图9

师生活动：立体几何问题中常见的模型有长方体模型、三棱锥模型，而鳖臑就是一个典型的三棱锥模型，且能联系沟通长方体与三棱锥。

设计意图：明确鳖臑的产生，强化基本模型意识。

7.教材中来，高考中去。

问题8：（2015年高考湖北理科第19题）将底面为长方形且有一条侧棱与底面垂直的四棱锥称为“阳马”，将四个面都为直角三角形的四面体称为“鳖臑”，在如图10所示的“阳马”P-ABCD中，侧棱PD⊥底面ABCD，且PD=CD，过棱PC的中点E，作EF⊥PB交PB于点F，连接DE，DF，BD，BE。

图10

（1）证明：PB⊥平面DEF，试判断四面体DBEF是否为“鳖臑”，若是，写出每个面的直角；若不是，请说明理由；

（2）若平面DEF与平面ABCD所成二面角的平面角大小为，求的值。

师生活动：学生独立完成。教师通过巡视，发现学生解决问题期间产生的困难或错误，进行针对指导。

设计意图：巩固前面学习的内容，评价学生学习效果。

三、教学反思

1.在教学过程中，如果只是就题论题，学生往往容易陷入题海。但是如果能够认真分析，充分发掘问题的教育价值，从中发现基本图形，有的放矢，从而选择恰当的途径，获得更合理的解决方案。就像一棵树由树根、树干、树枝和树叶组成一样，“基本图形”属于树根和树干部分，有“自我生长能力”。在立体几何中“抓基本图形”是非常重要的。正方体、长方体、三棱锥是立体几何中最重要的基本图形，鳖臑作为特殊的三棱锥，既蕴含了丰富的垂直关系，又可以联系正方体、长方体，是立体几何的核心图形。

2.发现和归纳基本图形的主阵地应该有两个。一是教材，例如，本堂课选择的探究问题和例题全部来自教材。二是高考题，作业的两个问题都是高考原题。从这种角度来讲，只有教师先下题海，做题、归纳，才有可能从中分析找到基本图形，为学生提供了一个非常好的范例，努力做到“授人以渔”。充分发挥“基本图形”的力量，先“基本图形”再“变式图形”再“综合图形”，只有在连续而有逻辑关联的几何问题解决当中才能得到推理论证的技能训练，学会灵活运用几何概念、性质解决立体几何问题。

3.强调向量法的作用是立体几何改革的基本方向，也是解决立体几何问题的主要方法，但不能将其理解为一种程序性算法。向量法解题的第一步是用向量表示几何元素，“表示”合理才能保证后续运算的简捷。“合理表示”的本质是准确反映立体图形的特征，要以准确把握图形结构特征为基础。

4.高考题的命题一定是源于教材，并高于教材。高三复习课一直强调回归课本，只有在复习的过程中向学生揭示高考题与教材原型的关系，才能正确引导学生回归课本。总之，课本是使学生学做人做事的基本载体，脱离课本的教学不是好的数学教学。教师最基本且重要的职责是教好课本。只有从中发现基本图形，掌握基础概念，踏实训练，才是提高学生数学能力的捷径。