多部件重要度系统机会维修策略的优化
薛朝改,谷 雨,曹武军,曹海旺
(1.郑州大学管理工程学院,河南 郑州 450001;2.郑州航空工业管理学院机电工程学院,河南 郑州 450046)
1 引言
在多部件的设备中,由于各个部件故障率的差异性,导致了系统内部件的最佳预防维修间隔期也是有差别的。因此,对系统进行预防性维修时如果单单考虑每个部件的最佳维修间隔期,则不可避免的会导致系统屡次停机,浪费更多的费
用对系统进行维修。机会维修是指对系统内故障部件进行维修时,提前对系统中短时间内需要维修的其他部件一并进行预防性维修或者更换[1]。
关于系统机会维修的研究大多是探究机会维修的阈值[2],文献[3-4]基于部件的可靠性,进而判断系统的机会维修阈值问题。文献[5-6]把部件的役龄设为系统进行预防性维修的阈值。文献[7]是以部件的故障概率为基础,通过考虑探究设备状态检修对系统可靠性要求的负荷指标的影响进而建立相应的模型
并进行分析。文献[8]是以部件的故障率作为判断是否对系统进行机会维修。文献[9-10]综合考虑了多个部件之间复杂的相关性,进而寻求最优维修策略最大程度的降低系统的运行成本。文献[11-12]基于部件的预防性维修间隔期来确定系统中的部件是否需要机会维修。上述文献大多是建立在以系统运行成本最低,系统可用度满足一定条件为基础上的机会维修策略,但是没有考虑不同部件对系统可靠性的影响也不同。
为了降低系统在运行周期内的维修费用并且提高其可用度,这里通过引入系统的机会维修系数和部件的Birnbaum重要度,基于各个部件的预防性维修间隔期,分析系统在运行周期内的可用度以及总的维修费用,进而建立多部件串联系统机会维修优化模型,通过引入部件的Birnbaum重要度后可以判断出是否降低了系统在有限运行周期内的维修成本并且提高系统的可用度。
2 系统描述
2.1 机会维修策略的描述
这里研究的对于系统内需要维修的部件所采用的维修方式分为三种。分别为机会维修,预防性维修以及故障维修。系统内的部件在进行机会维修和预防性维修之后,其故障率会有一定程度的变化。对于系统中发生故障的部件,立即对故障部件进行维修,其故障率在维修之后不发生任何变化。将r设为系统的机会维修系数,假定在t时刻,系统内的部件k最先达到了其最佳预防维修间隔期的阈值,因此部件k需要进行预防性维修。此时,部件l(l≠k)所处其第i个预防维修间隔期内,T′il为t时刻部件l在第i个预防维修间隔期内所使用的时间。
2.2 Birnbaum重要度
Birnbaum重要度描述了部件从工作状态到故障状态,系统可靠性的变化值。Birnbaum重要度的计算公式如式(1)所示,式(1)的结果越大,说明部件Cl从工作状态(Cl=1)变为失效状态(Cl=0)时,系统S的可靠性R(.)所受到的影响就越大。说明该部件对于系统越重要。
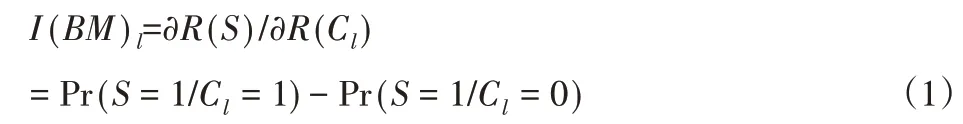
2.3 符号意义
注解:i—部件l的第i个预防性维修间隔期;
Til—部件l完成第i-1次预防性维修与第i次预防维修结束后所间隔的时间;
hil(t)—部件l第i-1次预防性维修与第i次预防维修的故障率函数关系式;
ɑil—部件l的役龄递减因子,且0<ɑil<1,bil>1为故障率递增因子;
tpl—部件l进行一次预防性维修所花费的时间;
tfl—对部件l实施一次故障维修所花费的时间;
Cpl—对部件l实施一次预防性维修所花费的费用;
Cfl—对部件l实施一次故障维修所花费的费用;
Cel—部件l单位时间的停机所造成总的损失费用;
Cgl—对部件l每次更换所花费的费用;
tln—在系统第(n-1)次预防性维修后,部件l(l=1,2,3…,S)所需要进行维修的时刻;
tn—对系统第n次实施维修的时刻,tn=min(t1n,t2n,t3n…tln);
nl—截止到tn时刻,部件l总共的预防性维修次数;
hl(nl+1)—部件l第nl次预防性维修与第nl+1次预防性维修故障率函数关系式;
T′il—在时刻t部件l在其所处的预防性维修周期内使用的时间;
tpltn—时刻tn对部件l进行维修所需要花费的时间;
tgltn—时刻tn将部件l进行更换所花费的时间;
Tpdn—系统在第n次预防性维修所需要停机时间Tpdn=max(tpltn,tgltn),1≤l≤S;
T—设为系统的运行周期时间;
N—[0,T]时间段内系统进行维修的次数。
2.4 系统模型假设
(1)系统是由S个串联的部件构成,系统内所有的部件起始时均为新的部件,系统中S个部件都服从威布尔分布。机会维修是以系统内部件的预防性维修为前提。
(2)维修资源能够保证维修任务的完成,在维修的过程中不用考虑维修资源的限制。
(3)如果系统内的某些部件出现意外故障,马上采取措施对故障部件进行维修,无论对系统内的部件进行任何方式的维修均会引起系统停机。
3 基于Birnbaum重要度的多部件串联系统机会维修优化模型
3.1 单部件维修间隔期求解
部件的可靠性随着其预防性维修次数的增加而减小,因此需要把部件的故障率递增因子和役龄递减因子考虑进去,部件在第i次预防性维修前后故障率的函数表达式为:
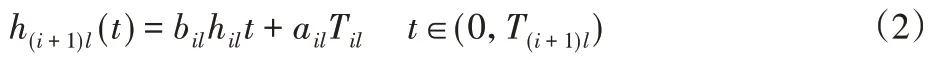
把l部件看作是系统中任何一个部件,如果部件l的预防性维修次数达到Nl+1次,那么直接将其更换为新的部件。部件l的故障维修采用最小维修方式,可以确定出部件l在其第i个维修间隔期内所需要维修的时间为:

部件l在第i个维修周期内的可用度为:
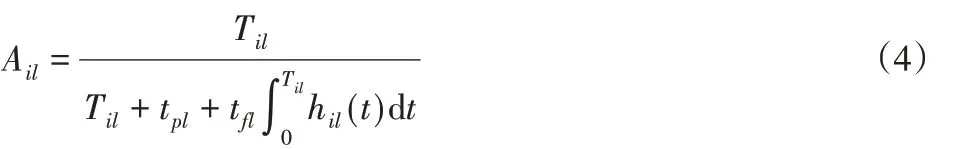
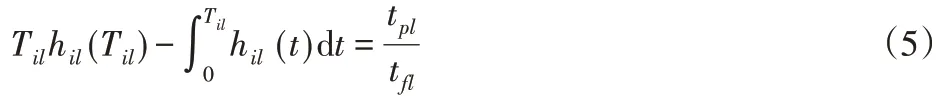
结合Matlab仿真分析,能够计算出Til的具体数值解。
部件l单位时间的维修费用为:
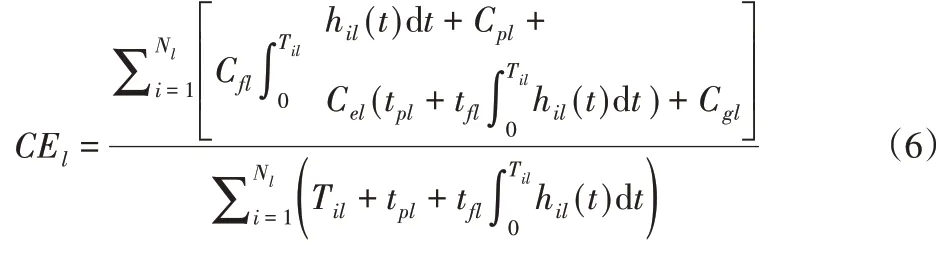
使式(6)的值最小,能够求出部件l最佳的预防性维修次数Nl。
3.2 分析系统总的维修费用和系统的可用度
系统在运行周期内总的维修费用包括两部分。第一部分为对系统内的部件进行维修所需要的费用,第二部分为由于对系统内的部件进行维修所造成的停机损失费用。部件l在第(n-1)次预防性维修完成到第n次预防性维修后,在这段时间内,部件l的直接维修费用Cpln共包含三部分。分别为部件l的预防性维修费用Cpl,部件l的更换费用Cgl,以及部件l的故障维修所需的费用Cfl。Cl表示对于系统内的部件l进行维修所需要的费用,则Cl=
系统在运行周期内的停机时间Td包括两部分。第一部分为系统内的部件进行预防性维修所造成系统的停机时间Tpd,第二部分为由于系统内的部件突然出现故障所造成系统的停机时间Tfd。当系统在第n次预防性维修时,其停机的时间Tpdn=max(tpltn,tgltn),1≤l≤S。设系统单位时间的停机损失费用为Cd,那么系统在运行周期[0,T]内的停机损失费用为:

假设ml为部件l在系统运行周期[0,T]内所需要进行的预防性维修次数,设ml=PNl+q(p,q=0,1,2....);Tjl(j=1,2,3,....ml)代表为部件l在其每个预防维修周期内所使用的时间。Tfdl代表部件l在系统运行周期[0,T]内发生意外故障所造成的系统停机时间,那么部件l在系统运行周期[0,T]内系统的意外停机时间为:
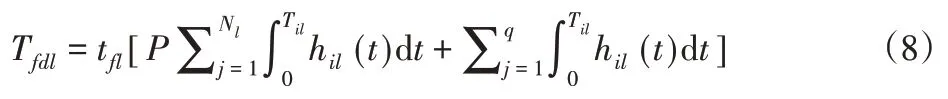
系统在运行周期[0,T]内发生意外故障的停机费用为:

系统在运行周期[0,T]内总的维修费用为:
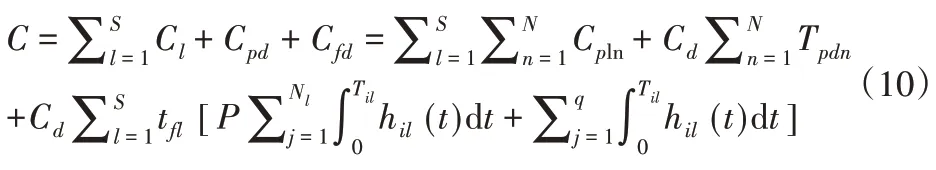
系统的可用度表示为系统在运行周期内其工作的时间与总时间的比值。那么系统的可用度可表示为:
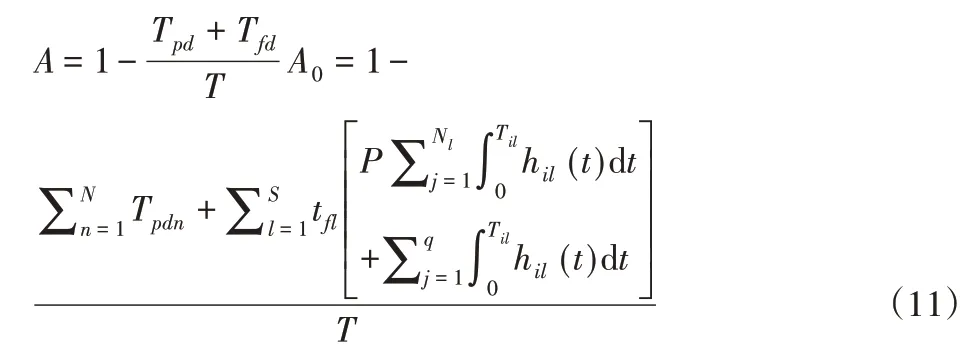
3.3 基于Birnbaum重要度的多部件串联系统机会维修优化模型的构建
对于系统内Birnbaum重要度较大的部件,需要更加频繁的对其进行维修。从而降低系统在运行周期内的维修成本。因此,将系统内部件的Birnbaum重要度引入到公式中,通过比较值的大小来判断部件l是否需要进行预防性维修,根据式(1)系统中部件的Birnbaum重要度是随时间变化的连续函数,因此这里将部件的Birnbaum重要度做如下的转换,即表示为部件的Birnbaum重要度在系统运行周期内积分的均值:

引入机会维修系数和各个部件的重要度,以系统在运行周期T内总的维修费用最低为目标,以系统的可用度达到一定的要求为条件。机会维修优化模型可表示为:
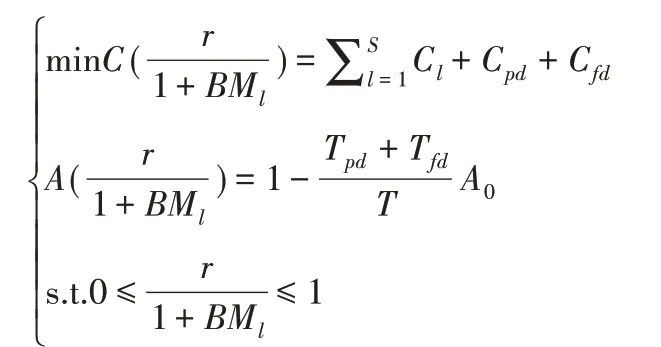
式中:A0—系统需要达到的最小可用度。通过运用Matlab仿真分析可以得出最优的机会维修次数;C—相应的维修成本。
4 算例分析
系统共包含均服从二参数威布尔分布的六个部件,h(t)=(β>0,η>0),β代表为部件的样式参数,η代表为部件的长度参数。系统因为停机所引起的损失费用为Cd=1500/天,要求系统达到的最小可用度为92%。系统内所有部件的故障率递增因子和役龄递减因子都一致,计算为:

系统各部件其他参数[12],如表1所示
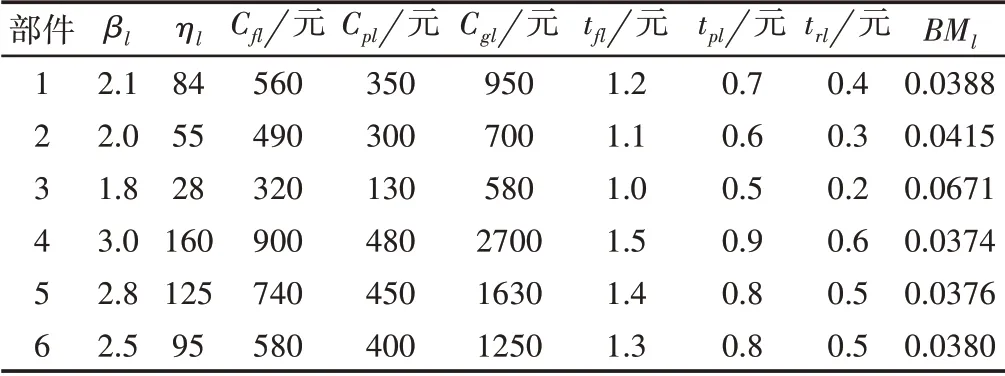
表1 部件参数Tab.1 Component Parameter
设定系统的模拟运行周期为[0,533]天,当考虑部件的重要度时,使用MATLAB对所构建的多部件串联系统机会维修模型进行仿真分析,当r<0.42时,其仿真结果与不考虑机会维修相差太大,当0.42≤r≤1时,随着机会维修系数r的变化,总的维修成本C与可用度A之间的关系,如图1所示。其仿真的结果如表2所示。
当不考虑部件的重要度时,使用MATLAB编程对模型进行仿真,当r<0.40时,其仿真结果与不考虑机会维修相差太大,当0.40≤r≤1时,其仿真结果,如表3所示。随着机会维修系数r的变化,系统总的维修费用C与可用度A之间的关系,如图2所示。分析表2、表3、图1、图2可知,随着机会维修系数r的逐渐增大,系统的可用度A先呈递增趋势,达到某一最大之后呈递减趋势,系统总的维修费用先逐渐减小,达到某一最小值后逐渐增大。
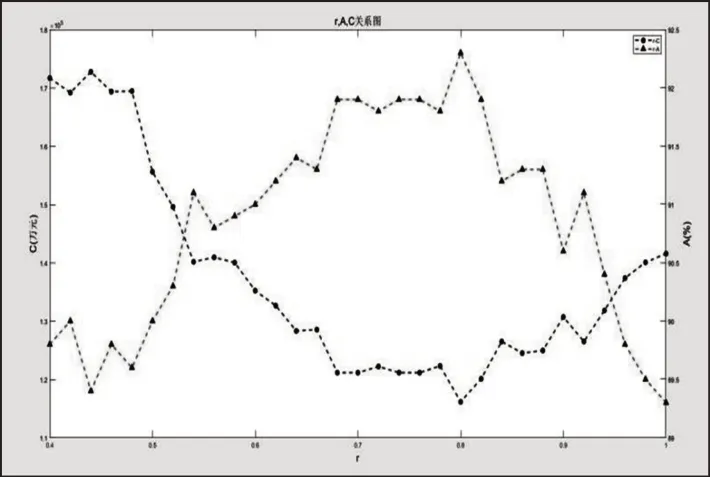
图2 r与总维修成本C和可用度A的关系图Fig.2 The Diagram of r to the Total Maintenance Cost C and Availability A
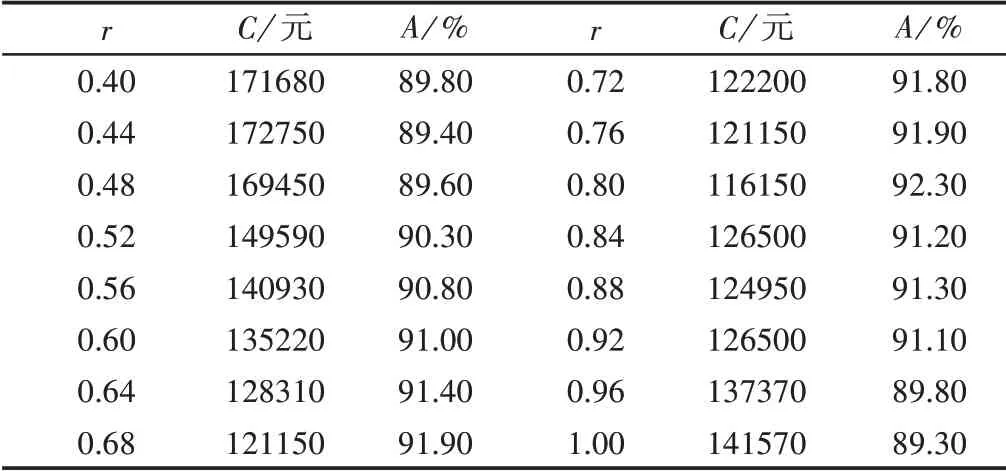
表3 模型仿真的结果Tab.3 Model Simulation Results
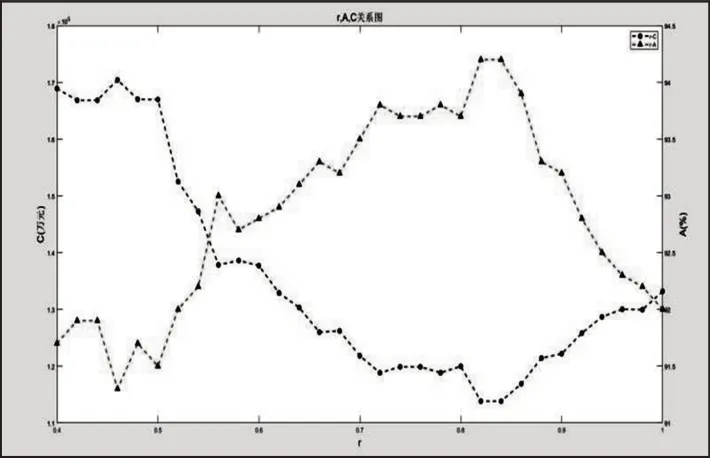
图1 r与总维修成本C和可用度A的关系图Fig.1 The Diagram of r to the Total Maintenance Cost C and Availability A
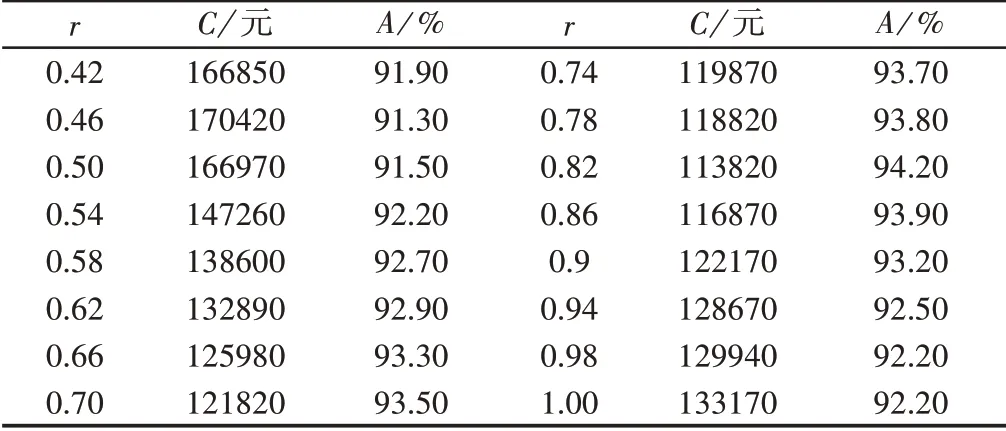
表2 模型仿真的结果Tab.2 Model Simulation Results
如表4所示,当多部件串联系统考虑部件的重要度时,由运算结果可知,r=0.82时为最优机会维修系数,此时设备总的维修费用最小,为C=113820,可用度为94.20%。当系统不考虑部件的重要度时,由运算结果可知,r=0.80时为最优机会维修系数,此时设备总的维修费用最小,为C=116150,可用度为92.30%。在系统运行的533天周期内,系统考虑部件的重要度与系统不考虑部件的重要度相比,可节约维修费用2.04%,系统的可用度提升了1.90%。当r=0.82时,系统内各个部件的具体维修方案,如表5所示。
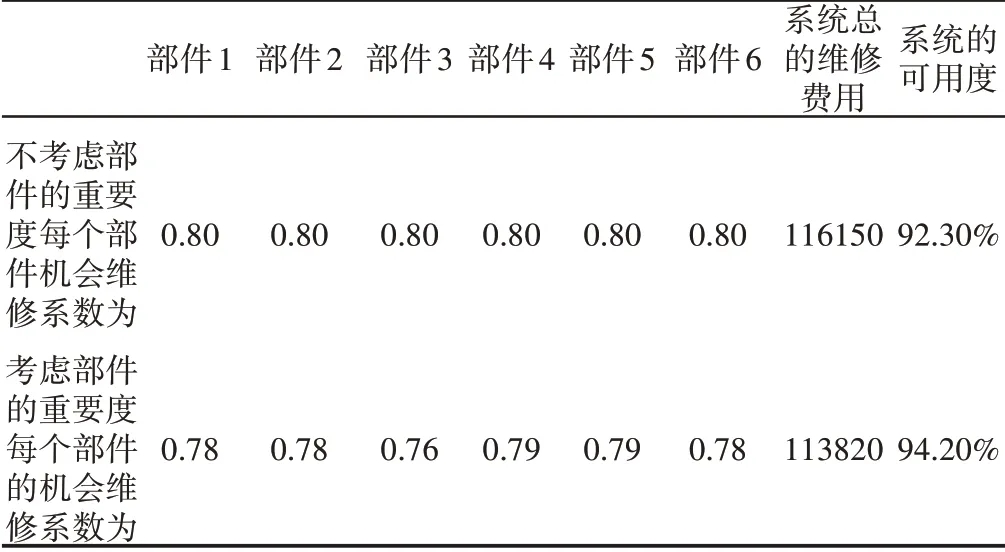
表4 两种维修决策下系统维修费用和可用度的比较Tab.4 Comparison of System Maintenance Cost and Availability Under Two Maintenance Decisions
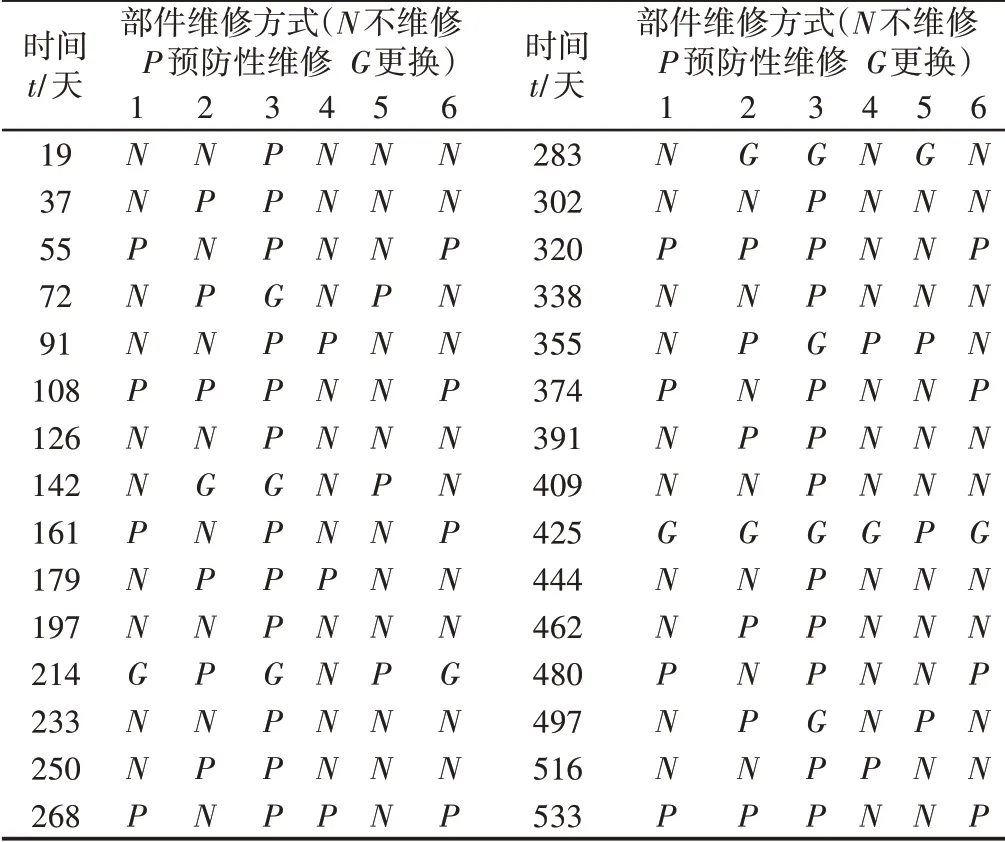
表5 系统中各部件的维修计划Tab.5 Maintenance Plan for Each Component in the System
5 结论
这里在原有机会维修的基础上,引入机会维修系数和部件Birnbaum重要度的概念,分析了由多个不同Birnbaum重要度部件所构成的串联系统在运行周期内的可用度和总的维修费用,构建了基于重要度的多部件串联系统机会维修模型。通过算例分析证明,引入部件的重要度之后构建的机会维修优化模型与不探究部件的重要度相比,能够使系统在运行周期内减省较多的维修费用,同时提升系统的可用度。这里所构建的基于重要度的多部件串联系统机会维修模型为系统考虑部件的重要度所做的最优维修策略提供决策支持。

