基于隐式动力学的起重机轮—轨摩擦系统振动分析
陈艳艳,刘跃昆,王志伟
(黄河水利职业技术学院,河南 开封 475004)
1 引言
随着门式起重机朝着大型化和高速化的发展,这对起重机轨道和车轮的强度、承载能力和使用寿命提出了更高的要求[1]。轮轨之间的摩擦作用直接影响到起重机的运行品质、效率和成本,尤其是当车轮与轨道之间发生“啃轨”现象时,轮缘和轨道两侧将会发生严重的磨损和变形,产生剧烈的振动噪声,对起重运输的稳定运行带来严重的安全隐患[2]。因此,深入理解起重机车轮与轨道之间的接触动力学行为,是提高起重运输稳定性的重要保证。
目前,研究者对起重小车与轨道之间的动力学特性展开大量研究[3-9],文献[3]建立起小车—轨道多体刚柔耦合动力学系统,采用Newmark-β逐步积分方法分析起重小车的运动速度、荷载质量等参数对结构振动以及荷载摆动的影响。文献[4]将起重机简化为单摆模型和四杆连接的复摆模型,并求解荷载的非线性摆动频率。文献[5]利用有限元软件ANSYS分析轮轨在不同载荷工况下接触应力的分布变化情况和轨道直线度异常对轮轨接触状态的影响,为实际存在的问题提供解决方案。文献[6]对轮轨间的接触—碰撞行为进行数值模拟,计算得到接触区应力分布的等值线图和应力变化时程曲线,并发现车轮与轨道的接触区存在渗透,在重载低速工况下可能发生冷焊黏着现象。文献[7]等采用有限元分析法研究了摩擦系数和滑动速度对起重机轮轨温升的影响,结果发现起重机最高温升发生在车轮接触面上,轨道上的温升较低,其温度场分布为一条长轨迹。文献[8]探讨了车轮的水平/垂直倾斜超差、车轮跨距、不等对角线和车轮的安装等因素与“啃轨”现象之间的联系,并提出合理的“啃轨”解决方法和对策。
以上研究对认识起重机系统的动力学特性意义重大。但关于起重小车轮—轨之间由于摩擦而形成的自激振动问题却鲜有报道。起重小车作为货物运输的承载体,车轮与轨道之间产生的滚动摩擦在一定时刻会形成摩擦自激振动,影响小车的运行稳定性[10]。此外,目前建立的起重机轮—轨接触模型通常只由单轨和单轮组成,忽略了轮对之间受力不均匀对系统稳定性的影响,具有一定的局限性。因此,有必要建立起更加完善的轮—轨接触系统模型,系统地开展起重小车与轨道之间摩擦振动特性的研究,为改善门式起重机系统的稳定性提供一定的理论基础。
基于以上考虑,本研究建立起某门式起重机有限元模型,在主梁上建立相应的轨道和小车轮对,采用隐式动力学分析法模拟车轮在轨道上的摩擦滚动的动力学行为,对车轮与轨道产生的动力学信号进行分析探讨。进一步地,对左右车轮受力不均的现象展开讨论,探索左右车轮受力不均对小车运行稳定性的影响。本研究结果对认识起重机的稳定性具有一定的意义,并能为改善起重机摩擦振动问题的结构设计提供参考。
2 车轮—轨道耦合有限元模型
2.1 有限元模型
门式起重机主要由主梁、支腿、小车轨道、轮对等部件组成。在SolidWorks中建立起重机各部件的三维模型,并导入有限元软件ABAQUS中进行装配与分析前处理。三维模型,如图1(a)所示。起重轨道总长29m,为了消除轨道边界对小车动力学行为的影响,将轮对放置于轨道中部。轨道间距2.26m,车轮半径380mm,轮轴总长2.638m。需要说明的是,本研究为提高计算效率,同时保证计算的精度,因此对非接触区的部分尖角进行一定的简化。
本研究中起重机系统有限元模型,如图1(b)所示。对轮—轨接触区域进行局部放大显示。部件网格主要采用C3D8单元,即8节点六面体单元,局部不规则区域采用C3D4(4节点四面体)单元过度,以提高计算效率与计算精度。各部件网格特征统计,如表1所示。
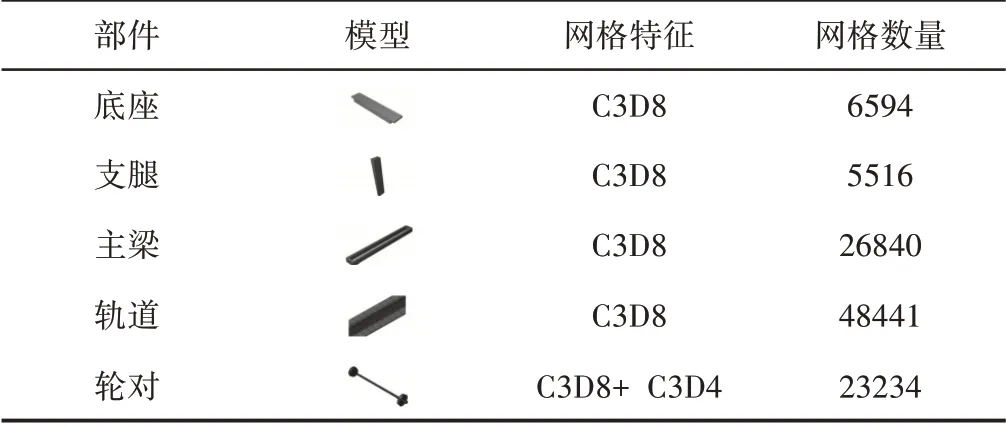
表1 有限元模型部件网格特征Tab.1 Mesh Characteristics of Finite Element Model Components
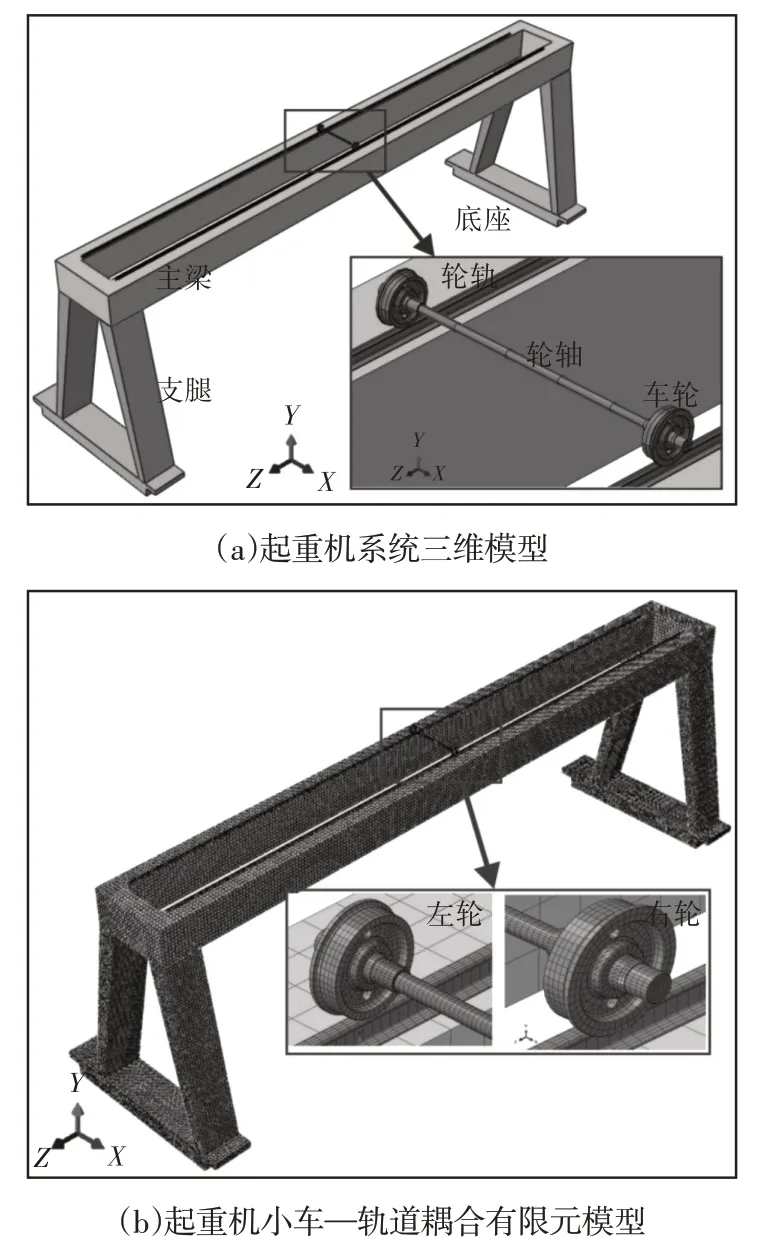
图1 门式起重机三维模型与有限元模型Fig.1 3D Model and Finite Element Model of Gantry Crane
模型载荷、接触与边界条件设置,如图2所示。轨道与主梁之间设置为绑定(Tie)约束,约束底座底面在平动和转动所有方向上的自由度,确保其处于固定状态。轨道顶面和车轮表面分别设置为Master surface(主面)和Slave surface(从面),定义接触面间的摩擦系数为0.45。轮轴两侧顶点设置为参考点,即Rp1与Rp2,设置两参考点与轮轴端部为动力学耦合约束,对参考点分别施加一定的载荷,模拟运输荷载。在预定义场(Predefined Field)设置中,对轮对施加一定的转动速度(6.28rad/s)与移动速度(1040mm/s),从而实现车轮在轨道上的滚动。

图2 起重机小车—轨道耦合有限元模型及边界条件Fig.2 Boundary Conditions of Crane Trolley-Track Coupled Finite Element Model
2.2 隐式动力学分析
在ABAQUS隐式动力学分析中,小车与轨道摩擦系统的运动方程可表示为[11]:

式中:[M]—质量矩阵;
Fin—结构受到的内力;
Fout—结构受到的外力,将隐式积分算子代入式(1)中,得到:

采用Newmark算法对式(2)进行积分运算。系统运动的位移和速度向量表示为如下所示:
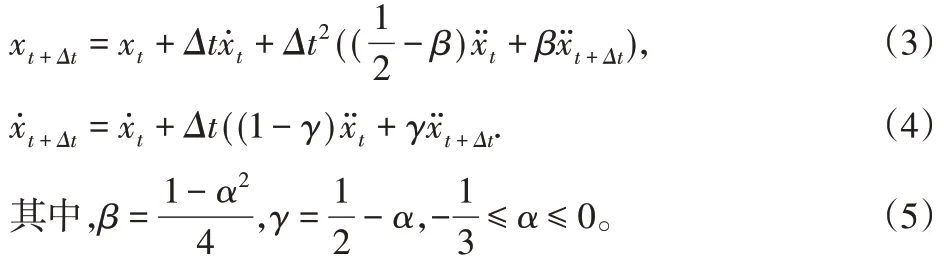
本研究主要有两个分析步:
(1)在车轴两端施加一定的载荷,使得小车车轮与轨道建立接触,模拟小车的初始接触状态;
(2)定义隐式动力学分析步骤,模拟起重小车在轨道上滚动的过程,并提取相应的振动信号进行分析。
3 小车—轨道耦合模型自然频率分析
本研究首先提取系统前200阶自然频率与模态振型进行分析结果,如图3所示。可见系统的模态频率从4Hz逐渐增大至500Hz,涵盖范围较广,这是由于门式起重机主要表现为类似两端固定的简支梁结构,极易出现梁式的各类扭转和弯曲振型。这也说明,当小车在轨道上运行时,由于摩擦力的作用,系统由于自然频率覆盖范围广而容易产生某种或某几种频率的自激振动。
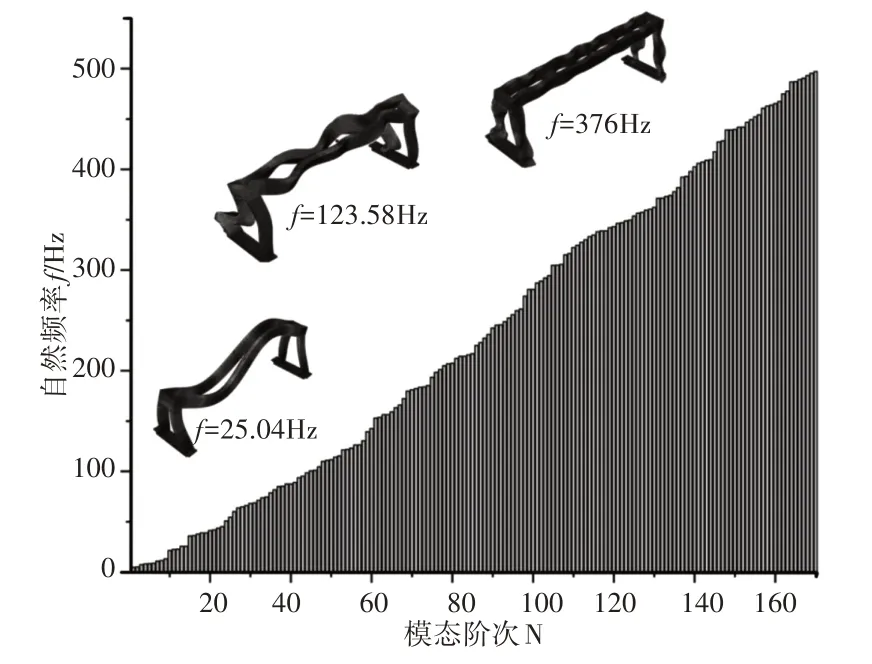
图3 起重机小车—轨道耦合模型自然频率Fig.3 Natural Frequencies of Crane Trolley-Track Coupling Model
进一步对不同频率范围内的典型模态特征进行分析,可知当模态频率较低时,系统的模态振型主要表现为起重机主梁/轨道的弯曲变形,这也说明了梁式结构在低频状态下容易被激发产生弯曲振动。在中频阶段,系统的模态振型主要表现为起重机主梁/轨道的弯曲扭转复合变形,系统的振型更加复杂。在相对高频阶段,系统的模态振型则表现为起重机主梁—轨道—车轮三者的耦合变形,各个部件以自身特有的振型进行叠加。综合以上分析可以推测,起重机的自然模态存在主梁—轨道—车轮三者耦合运动的形式,在摩擦力的作用下,车轮与轨道之间将会产生某特定频率和特定振型的摩擦振动现象。
4 瞬态动力学分析
4.1 振动信号时域分析
由于轮对左右对称,因此本部分取左侧车轮与轨道的动态响应进行分析,选取模型中的A和B两进行分析,其中,A点位于车轮表面,B点位于轨道表面,观察点设置,如图4所示。点A(车轮区)的振动时间历程图,如图5所示。可见在小车车轮在与轨道摩擦滚动过程中,车轮侧向(x向)偏摆严重,在x向产生了持续的摩擦自激振动现象,轮—轨之间有可能产生明显的“啃轨”现象。相比之下,车轮的切向振动和法向振动强度相对较弱,且主要出现在车轮运动的初始阶段,随着滚动摩擦的进行,切向振动和法向振动逐渐趋于稳定,这说明小车在启动过程中,系统的摩擦自激振动最为剧烈。此外,可见系统的切向振动明显大于法向振动,其中切向振动加速度幅值可达40m/s2,这说明小车在轨道上滚动过程中,其切向摩擦振动现象更加剧烈,这也使得所提升物体的切向偏摆现象更加剧烈,造成严重的安全隐患。
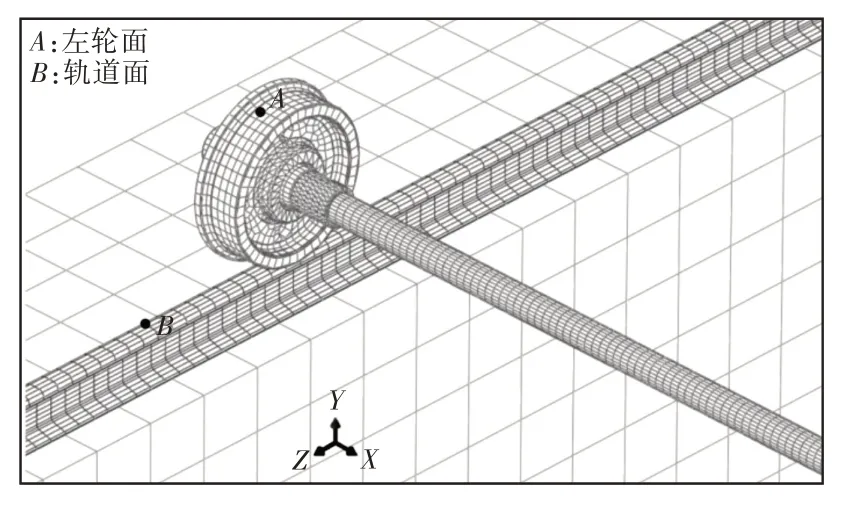
图4 振动信号观察点Fig.4 Observation Point of Vbration Signal
轨道上观测点B的振动信号,如图5(b)所示。可以看出,轨道上也产生了明显的摩擦振动现象,尤其是当车轮滚动通过轨道观测点区域时,轨道的法向和切向振动信号幅值显著增大。这也进一步证明了起重小车在滑过轨道时产生了明显的摩擦振动现象,这是车轮和轨道振动耦合作用的结果,是在摩擦激励作用下产生的车轮与轨道的共振。此外,轨道上的振动信号也表明,小车—轨道耦合系统的切向振动强度明显大于法向振动强度,这进一步证明了起重小车—轨道之间的摩擦振动是造成所提升物体切向偏摆的原因之一。只有充分认识起重小车与轨道之间的摩擦振动现象和产生机理,才能为改善安全起重运输的结构设计提供重要的理论支撑。
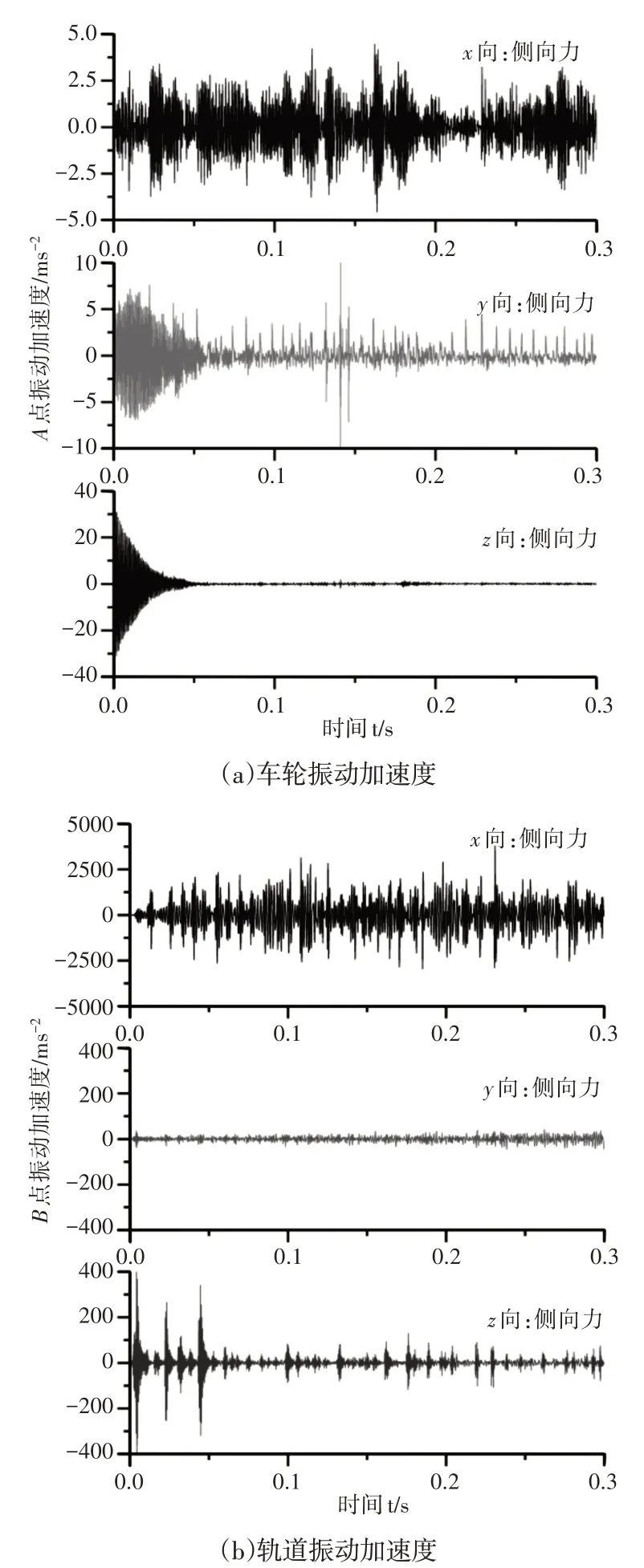
图5 起重机车轮—轨道耦合系统振动加速度信号Fig.5 Vibration Acceleration Signal of Crane Wheel-Track Coupling System
4.2 振动信号频域分析
进一步地,对车轮振动信号和轨道振动信号进行FFT分析结果,如图6所示。可见车轮的振动信号主要有两个主频,即566.47Hz和1152Hz,如图6(a)所示。其中1152Hz具有的振动能量明显较大,这表明在轮—轨摩擦过程中,车轮极易产生高频振动。对轨道的振动信号进行分析结果,如图7(b)所示。可见轨道的振动频率为566Hz和729Hz,在1100Hz左右的振动能量较低。综合以上分析可知,车轮与轨道均能够产生频率约为566Hz的振动,因此该频率的振动是由于车轮与轨道之间相互作用而产生的耦合振动。此外,车轮由于其圆盘式结构,更易被激起高频振动,因此产生了1152Hz的振动频率,而轨道作为细长的梁结构,在与车轮摩擦过程中,产生了频率为729Hz的振动,故起重机轮—轨之间的摩擦振动具有多频复合的特征,是一种部件耦合与独立振动并存的非线性动力学振动行为。
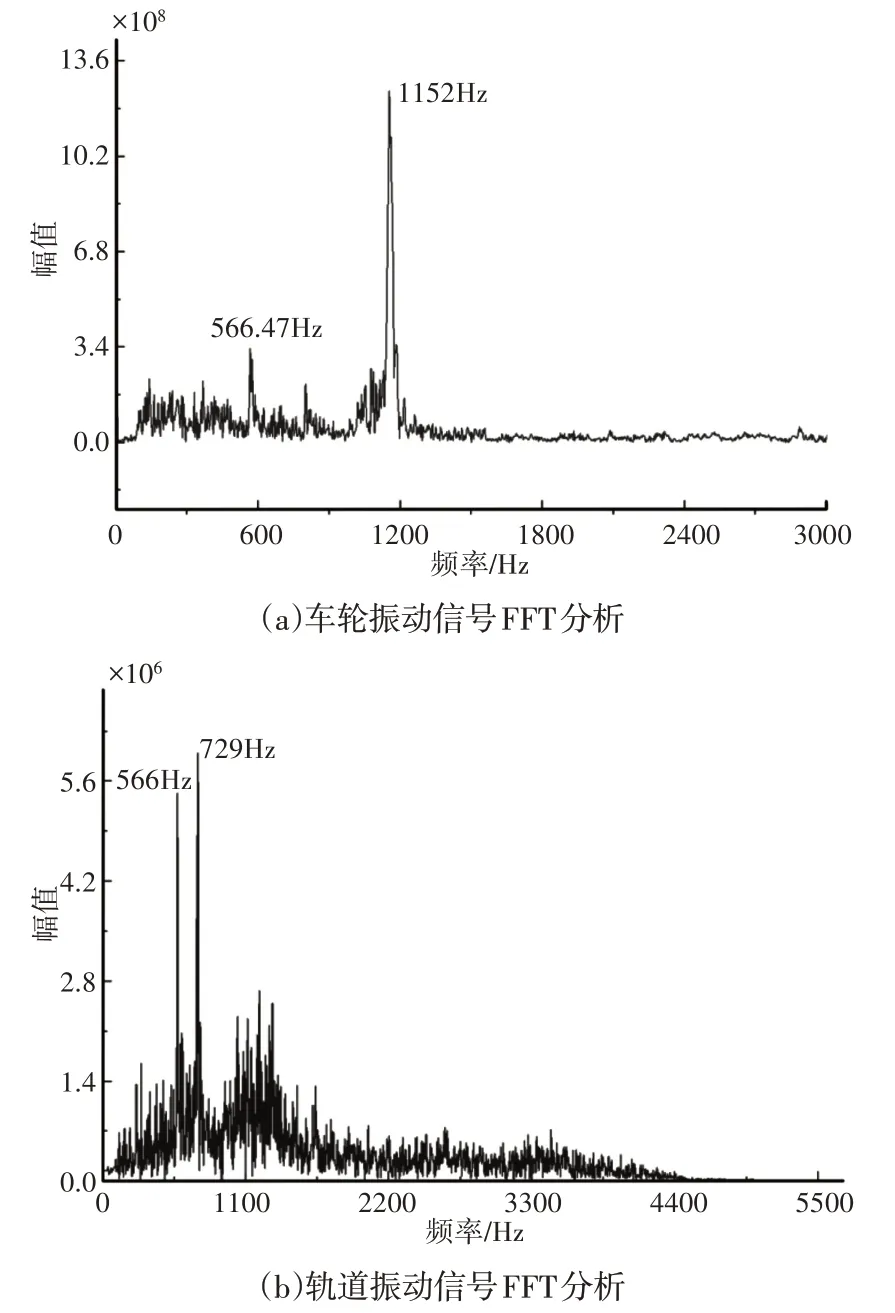
图6 小车振动与轨道振动信号FFT分析Fig.6 FFT Analysis of Trolley Vibration and Track Vibration Signals
5 轮对不对称力对系统振动影响分析
5.1 振动信号时域分析
考虑到起重小车在轨道上的运动过程中,通常假设重物的力是等值分配在轮对两侧。而实际运动过程中,可能由于吊装误差等原因导致轮对两侧受力产生差异,出现左右轮对受力不对称的现象,导致模拟结果产生误差,并导致更加极端的动力学现象出现。基于以上考虑,本部分对轮对受力不对称状态下的系统动力学行为展开研究,探明系统在受力不对称状态下,左右车轮与左右轨道可能出现的动力学行为。
假设小车左右车轮受力不等,如图7所示。其中,左侧车轮荷载20kN,右侧车轮荷载10kN。提取左右车轮上的观测点的振动信号进行分析结果,如图8所示。可见当左侧车轮载重大于右侧车轮时,左侧车轮的侧向(x向)振动明显大于右侧车轮,这说明载重更大的区域更有可能发生严重的“啃轨”现象,产生持续剧烈的侧向振动,导致车轮与轨道侧向接触面发生严重磨损,如图8(a)所示。对左右车轮法向(y向)和切向(z向)振动信号进行分析,在车轮运动的初始阶段,右侧车轮的法向(y向)和切向(z向)振动均大于左侧车轮,随着滚动摩擦的进行,左右车轮的切向振动和法向振动逐渐趋于稳定,没有产生明显的差异。这是由于左侧车轮载重较大,导致初始阶段右侧车轮与轨道的接触区域较少,在启动过程中,右侧车轮需要经过一定剧烈的振动达到新的平衡状态,进而实现稳定运动,因此其右侧车轮在法向和切向上振动均较左侧车轮更为剧烈。

图7 左右车轮载重不对称示意图Fig.7 Diagram of Asymmetrical Load of Left and Right Wheels
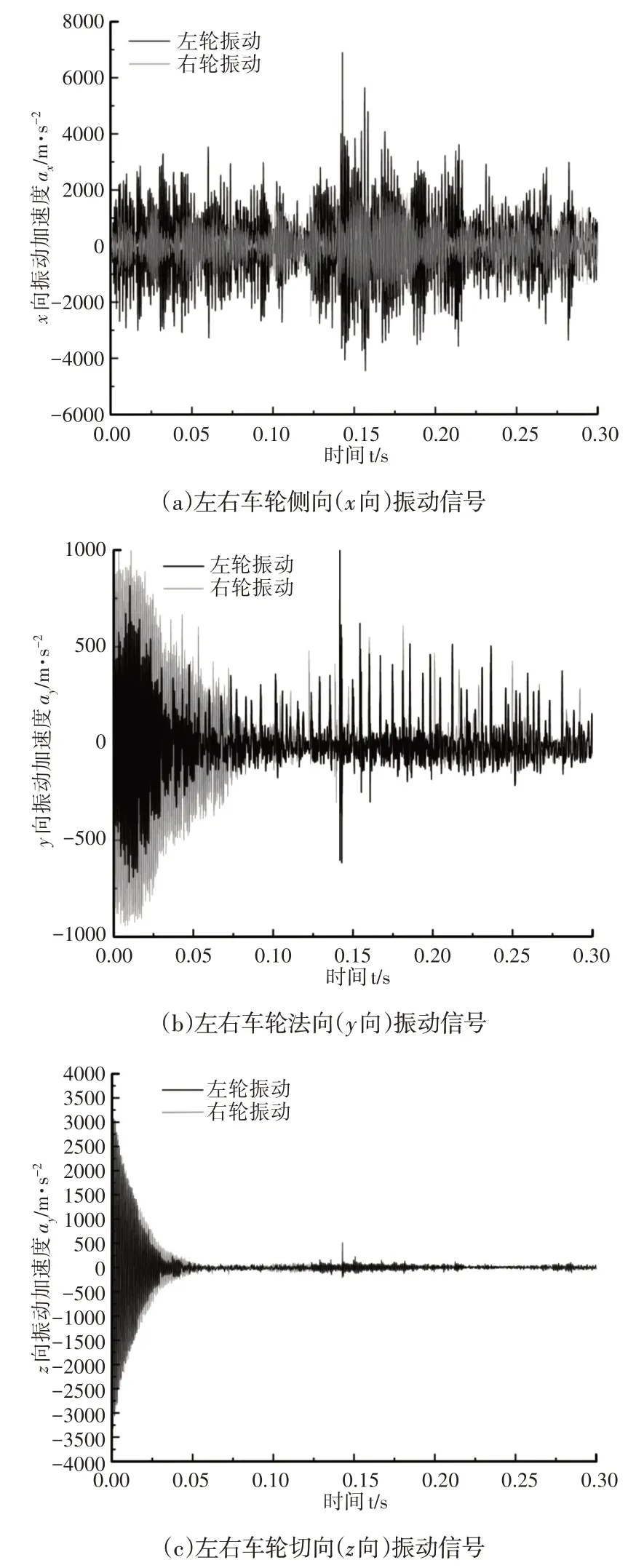
图8 轮对振动信号分析Fig.8 Vibration Signals Analysis of Left and Right Wheels
因此,当车轮对受力不对称时,载重较大的一次侧向振动增强,“啃轨”出现的可能性高。载重较小的一侧,车轮切向振动和法向振动在初始阶段波动更为剧烈,稳定后左右车轮的车轮切向振动和法向振动趋于一致。
进一步地,提取左右轨道上的接触应力进行分析结果,如图9所示。由于左侧车轮载重大于右侧车轮,因此在初始阶段,左侧轨道的接触应力大于右侧轨道。随着滚动摩擦的进行,当t=0.15s时,此时左侧轨道最大接触应力>100MPa,而右侧轨道的应力值等于0。这说明,在滚动摩擦过程中,由于左右两侧载重不对称,因此轨道受力差异显著,在一定时刻,载重更小的右侧区域可能出现轮轨短暂分离的现象,导致该侧接触应力为0MPa。当t=0.25s时,此时左侧轨道最大接触应力为31.89MPa,而右侧轨道的最大应力值等于137MPa,明显大于左侧区域。这可能是由于右侧轮轨短暂分离后,迅速重新接触形成一定的冲击作用,导致右侧接触应力显著增大,这也解释了右侧车轮的法向振动加速度出现了多次间歇性的波动现象,如图8(b)所示。

图9 轨道的接触应力分析Fig.9 Contact Stress Analysis of Track
综合以上分析,可知当车轮对受力不对称时,载重较大一侧的侧向振动增强,对于载重较小的一侧,车轮切向振动和法向振动在初始阶段波动更为剧烈。同时由于载重不同,两侧轨道接触应力变化差异显著,载重更小的一侧可能出现短暂的轮轨分离与轮轨重新接触的现象,从而导致接触力瞬时下降为0MPa与瞬时增大至大于100MPa。这导致起重机轮轨系统的最大应力位置随着时间不断发生变化,从而导致起重运输过程中的运输不稳定现象严重,带来严重安全隐患。
6 结论
本研究采用隐式动力学分析法,研究了起重机小车在轨道上滚滑过程中产生的摩擦振动现象,并对左右车轮受力不对称的现象展开讨论,研究结果如下:
(1)起重机系统低频模态表现为主梁/轨道的弯曲变形,中频模态表现为起重机主梁/轨道的弯曲扭转复合变形,高频模态表现为主梁—轨道—车轮三者的耦合运动。在摩擦力作用下,车轮与轨道之间将会产生某特定频率和特定振型的摩擦振动现象。
(2)在车轮与轨道摩擦过程中,车轮侧向产生持续的摩擦自激振动,轮—轨之间可能产生“啃轨”现象。车轮的切向振动和法向振动强度相对较弱,主要产生在车轮运动的初始阶段,且切向振动强度明显大于法向振动,可能导致所提升物体的切向偏摆更加剧烈。
(3)频域分析结果表明,起重机轮—轨之间的摩擦振动具有多频复合特征,是部件耦合与独立振动并存的非线性动力学行为。
(4)受力不对称状态下,车轮载重较大一侧的侧向振动增强,车轮载重较小一侧的切向振动和法向振动在初始阶段波动更为剧烈。载重更小的一侧可能出现短暂的轮轨分离与重新接触现象,这导致起重机轮轨系统的最大应力位置随着时间不断发生变化,带来严重的安全隐患。

