基于Adams软件的抓料机油缸铰点位置优化
□ 郭兰满 □ 刘云翔 □ 陈 林
三一集团湖南三一港机研究院 长沙 410100
1 优化背景
抓料机是一种多用途高效物料起重处理设备,主要用途是进行散杂货的装卸及转运,其工作装置主要由动臂和斗杆组成,通过动臂油缸和斗杆油缸的协调动作,实现物料的抓取和装卸。抓料机工作装置如图1所示。抓具的额定载荷是抓料机的主要性能参数,主要取决于动臂和斗杆的铰点位置分布,以及驱动油缸的几何参数。笔者建立抓料机工作装置的力学模型,基于Adams软件对动臂铰点位置进行试验研究,实现铰点位置的优化设计。
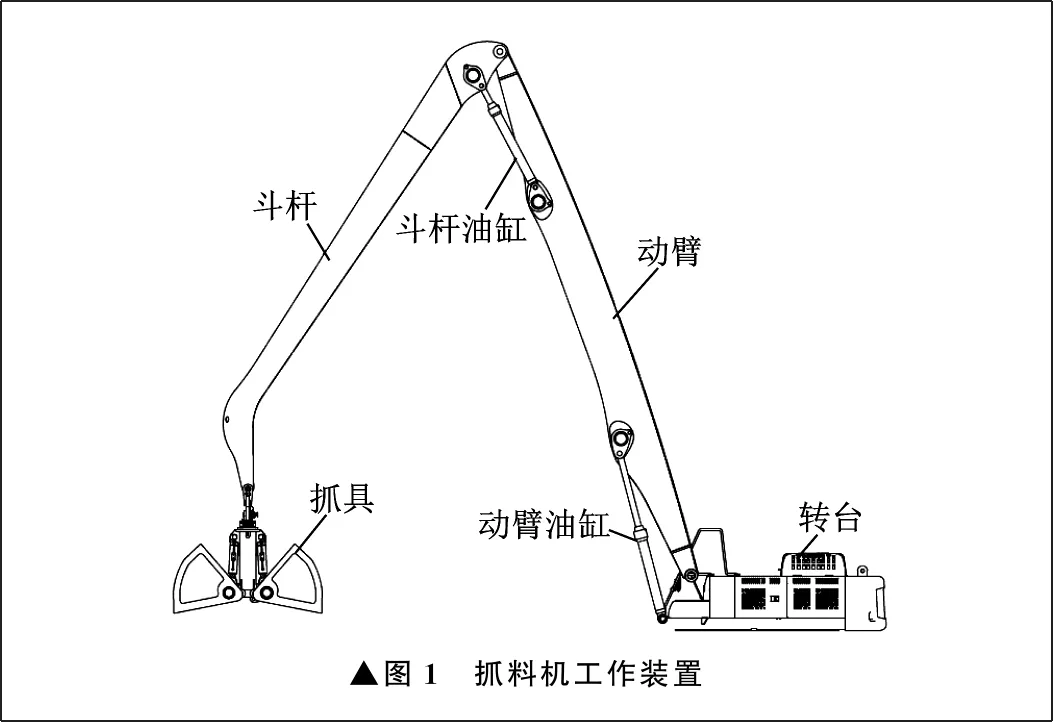
▲图1 抓料机工作装置
2 力学模型
建立抓料机工作装置力学模型,如图2所示。

▲图2 抓料机工作装置力学模型
O为动臂与转台铰点、坐标原点,A为动臂与斗杆连接铰点,B为斗杆与抓具连接铰点,C为动臂油缸与转台连接铰点,D为动臂油缸与动臂连接铰点,E为斗杆油缸与动臂连接铰点,F为斗杆油缸与斗杆连接铰点,M为动臂质心位置,H为斗杆质心位置,F1为动臂油缸作用力,F2为斗杆油缸作用力,L1为动臂油缸作用力臂,L2为斗杆油缸作用力臂,G为吊点载荷,G1为动臂自重,G2为斗杆自重,l1为铰点A、B之间长度,l2为铰点O、A之间长度,l3为铰点O、M之间长度,l4为铰点O、D之间长度,l5为铰点C、D之间长度,l6为铰点O、C之间长度,l7为铰点A、E之间长度,l8为铰点A、F之间长度,l9为铰点E、F之间长度。
以O点为坐标原点,设定各铰点初始位置坐标为O(0,0)、A(XA,YA)、B(XB,YB)、C(XC,YC)、D(XD,YD)、E(XE,YE)、F(XF,YF),动臂质心为M(XM,YM),斗杆质心为H(XH,YH)。对工作装置绕O点求力矩平衡,忽略油缸自重,可得:
F1L1=GXB+G1XM+G2XH
(1)
G=F1L1-G1XM-G2XH/XB
(2)
(3)
(4)
XH=l2cosθ+l1sin[β1+(β+90°-θ)]
(5)
XM=l3cos(θ+β2)
(6)


▲图3 各铰点坐标
L1=(l4l6sinα)/l5
(7)

α=θ-θ1+θ2
(8)
(9)
由式(2)~式(9)可得动臂油缸在最大工作压力下的允许载荷G′1。
同样,对工作装置绕A点求力矩平衡,得到:
F2L2=G(XB-XA)+G2(XH-XA)
(10)
(11)

L2=(l7l8sinγ)/l9
(12)
γ=β-β3-β4
(13)
(14)
根据式(10)~式(14)可得斗杆油缸在最大工作压力下的允许载荷G′2。
为保证抓料机工作稳定性,同时需考虑倾翻载荷对抓料机额定载荷谱的影响。根据最不利倾翻条件确定最危险倾翻线,根据力矩平衡原理得到倾翻载荷作用下的允许载荷G′3。
综合考虑G′1、G′2、G′3,抓料机的最大载荷取三者中的最小值。
3 动臂铰点位置仿真优化
3.1 工作装置动力学仿真
根据G′1、G′2、G′3三者中最小值得到整个抓料机的载荷谱,从中提取由G′1计算的载荷谱进行动力学仿真,根据G′1载荷谱设定仿真路径,根据斗杆吊点路径确定动臂油缸和斗杆油缸的速度运行函数,从而可得动臂油缸工作压力曲线,如图4所示。
3.2 多变量试验设计
在某型抓料机整机实际坐标系中,O点、C点、D点初始绝对坐标值为O(-320,995)、C(-860,180)、D(-1 669、3 291)。因抓料机动臂和斗杆的长度已经确定,故仅对影响动臂油缸工作压力的两个油缸铰点C、D的坐标建立设计变量PC(PCX,PCY)、PD(PDX,PDY),实现参数化设计。PC、PD分别为C点、D点的参数化坐标。根据动臂油缸铰点空间位置,设计变量的取值范围按照相对值的方法确定,其中各变量下偏差设置为-50 mm,上偏差设置为50 mm。以动臂油缸工作压力的最大值作为目标函数,定义多变量试验设计,目标函数为max (F),参变量为(PCX,PCY,PDX,PDY)。
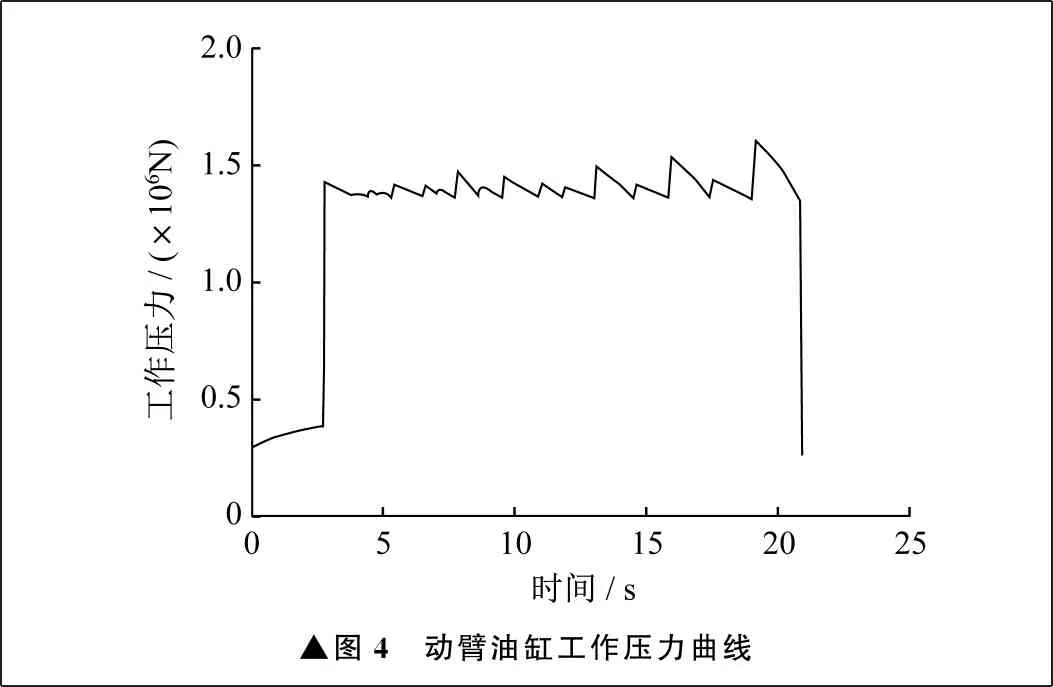
▲图4 动臂油缸工作压力曲线
基于Adams软件Insight模块可快速对多个设计变量进行试验分析,得到各个设计变量对目标响应的影响因子,从而针对影响因子较大的设计变量进行优化。基于以上六个设计变量建立因素集,并对目标函数进行试验设计,得到各设计变量对目标函数的影响因子,见表1。
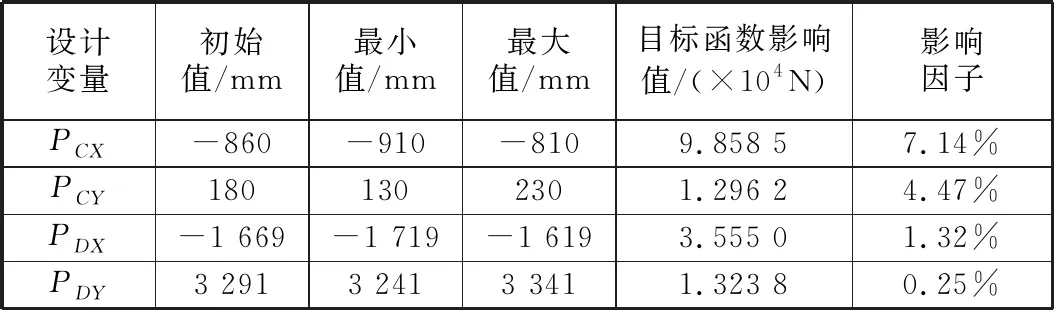
表1 设计变量对目标函数影响因子
由表1可知,PCX、PCY、PDX对动臂油缸工作压力影响较大,PDY对动臂油缸工作压力影响最小。
3.3 优化计算
针对试验设计中对动臂油缸工作压力影响大的三个变量进行优化计算,为使吊点在相同位置获得最大的额定载荷,优化目标为动臂油缸工作压力在迭代过程中取值最小,以获得最大的油缸工作压力裕量,从而使各吊点位置的允许载荷达到最大。定义优化目标为min (max(F)),设计变量为(PCX,PCY,PDX)。各变量下偏差设置为-50 mm,上偏差设置为50 mm。
某型抓料机的动臂油缸初始安装距为1 965 mm,行程为1 325 mm,建立动臂油缸与铰点变量lCD优化分析约束函数1 965 mm≤lCD≤3 290 mm。
基于Adams软件View模块进行优化计算,优化迭代结果见表2。
由表2可知,当PCX取值-910 mm,PCY取值130mm,PDX取值-171 9 mm时,动臂油缸工作压力最大值由1.602 4×106N减小为1.505×106N,减小幅度约为8%,动臂油缸工作压力优化前后的曲线对比如图5所示。

表2 优化迭代结果

▲图5 动臂油缸工作压力优化前后曲线
4 结束语
笔者建立抓料机工作装置力学模型,进行动力学仿真,基于Adams软件Insight模块分析了动臂油缸铰点各设计变量对目标函数的影响因子,为抓料机各部件优化提供了理论依据和方法。
另一方面,基于Adams软件View模块对目标函数影响最大的设计变量进行优化计算,得到动臂油缸铰点变量范围内的最优点坐标,动臂油缸工作压力最大值由1.602 4×106N减小为1.505×106N,减小幅度约为8%。若G′1为G′1、G′2、G′3三者中最小值,则抓料机允许载荷将有同等幅度的提升。
应用Adams软件进行机构的优化设计省时高效,可以得到精确、直观的载荷曲线及结果参数,为后续整机系统多目标函数联合优化奠定了基础。

