一种新型扭转金属阻尼器及其减震性能分析
王德斌 白海峰 付 兴 倪龙飞
(1大连交通大学土木工程学院, 大连 116028)(2大连理工大学建设工程学部, 大连 116024)
传统建筑主要依靠结构自身变形吸收地震能量的输入,导致结构主体构件损伤后难以及时修复.设置阻尼器可以有效耗散地震能量,避免主体结构过早进入塑性变形状态,从而降低甚至避免主体结构发生破坏.作为目前较为常用的消能减震装置,阻尼器具有一定的独立性,是结构抵御外部荷载的主要辅助耗能部件,其屈服变形甚至破坏不会影响主体结构的使用功能.因此,阻尼器在工程结构消能减震设计和既有建筑抗震加固中得到了广泛的应用.
现有金属阻尼器的耗能机制主要以弯曲、剪切和拉压变形为主.Demir等[1]提出了一种锯齿形耗能装置,具有稳定的滞回性能,不会出现突然的强度退化.Zibasokhan等[2]设计了一种纯弯曲变形阻尼器,具有良好的耗能能力,拉压状态下的滞回性能稳定,并未出现明显的非对称特征.Deng等[3]通过设置防屈曲约束板来避免剪切钢板的平面外屈曲,有效增强了剪切耗能钢板的稳定性,提高了剪切钢板的耗能能力.林煜等[4]设计了一种双拼工字形钢板阻尼器,可有效避免钢板平面外屈曲,并通过试验发现增强腹板宽度能够有效提高阻尼器的承载和耗能能力.邓开来等[5]提出了一种新型辊轴式金属阻尼器,由一组转动辊轴和一块平直耗能钢板组成,试验结果表明辊轴个数及其间隙决定了阻尼器的耗能性能,并给出了该阻尼器的恢复力模型.王威等[6]基于布置形式的改变,设计了2种波形软钢阻尼器,具有稳定的耗能性能和良好的塑性变形能力.
基于扭转变形引起的剪切屈服耗能是另一种能量耗散型阻尼器.相比传统弯曲、剪切型金属阻尼器,在外荷载产生的扭矩作用下,扭转型耗能阻尼器的截面应力、应变分布更加均匀,具有多截面屈服特点及较强的耗能能力.目前,基于扭转变形机制进行屈服耗能的阻尼器研究较少,且仅对管状[7]、圆柱形[8]金属阻尼器进行了分析,其主要通过阻尼器的剪切和扭转组合变形进行能量耗散,在非线性变形过程中存在明显的非均匀应力分布.Mahyari等[9]提出了一种新型纯扭转屈服阻尼器,通过有效利用阻尼材料的耗能能力,使其具有较好的吸能性能和延性,管壁应力分布均匀,等效阻尼比高达38%~48%.
针对现有金属阻尼器应力、应变分布均匀性差、易于发生局部屈曲破坏的缺点,本文设计了一种基于扭转变形机制进行屈服耗能的金属阻尼器,并基于理论分析推导出其初始刚度和屈服承载力的计算公式.对不同管材、不同壁厚的阻尼器力学性能进行参数化试验研究,采用ABAQUS有限元软件建立了阻尼器数值模型,并模拟出试验加载过程.最后,结合Y形支撑钢框架,对设有该阻尼器的支撑钢结构进行了抗震性能研究.
1 阻尼器构造及力学模型
1.1 阻尼器构造及工作原理
本文提出的阻尼器通过金属管的扭转变形进行屈服耗能.阻尼器主要由约束装置、加载控件、耗能金属管、转动力臂和转动轴承5个部件组成,各部件之间均通过M8.8级高强螺栓连接,具体构造见图1.图中,F为外荷载;Df、df分别为法兰的外径和内径;dz为转动轴承直径;L为转动力臂有效长度;Lp为耗能金属管有效长度;D、d分别为耗能金属管的外径和内径.每个阻尼器均设有4根耗能金属管,尺寸、形状、材料完全相同(见图1(b)).

(b) 阻尼器
为保证阻尼器工作过程中转动力臂仅发生转动位移,在加载控件和转动力臂连接处的转动力臂受载端开长孔,所设孔径与圆柱铰链直径相同.外荷载施加于加载控件端部,推动其进行往复运动,并通过圆柱铰链传力于2个转动力臂加载端,使其绕转动轴承转动,耗能金属管一端通过端部法兰固结于转动力臂之上,另一端则通过螺栓固结于阻尼器约束装置上.同时,转动轴承直径与转动力臂约束端轴孔直径相同,金属管法兰内径尺寸略大.转动轴承强度及刚度均远高于耗能金属管,施加的外荷载产生的等效集中力完全由转动轴承承担,附加力偶则使耗能金属管发生纯扭转变形.工作过程中,设置转动轴承时耗能金属管发生纯扭转变形;不设转动轴承时,则发生弯-剪-扭组合变形.为保证非耗能结构部分仅发生刚体平动或转动而无非线性变形行为,除耗能金属管外所有材料均采用高强钢材,以此避免耗能金属管之外的部件产生变形行为而造成附加约束力.
1.2 阻尼器力学模型
1.2.1 材料应力-应变关系
根据钢材标准单向拉伸试验数据,选取双线性强化材料本构模型(见图2(a)).基于Von-Mises屈服准则可以得到纯剪切应力状态下的切应力-切应变关系曲线(见图2(b)).图中,τy、τu分别为材料屈服切应力和极限切应力;γy、γu分别为材料屈服切应变和极限切应变;σy、σu分别为材料屈服应力和极限应力;εy、εu分别为材料屈服线应变和极限线应变;E为弹性模量;G为剪切弹性模量.由图可知,屈服切应力与屈服应力的关系表达式为
(1)
屈服切应变与屈服应变的关系表达式为
(2)
式中,ν为泊松比,本文后续试验中采用的Q345级钢和Al-6063A合金铝的泊松比分别取为0.30和0.33[10].

(a) 拉伸应力-应变关系

(b) 剪切应力-应变关系
1.2.2 内力扭矩与外荷载关系
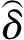
(3)
式中,T为耗能金属管内力扭矩.

图3 转动力臂位移变化示意图
小变形条件下,特别是初始屈服前,转动力臂与耗能金属管的转动变形较小,此时可认为外部施加位移与转动力臂转动位移相等均为δ,即存在如下关系:
(4)
本文中耗能金属管壁厚远小于其直径,因此在内壁发生屈服前,均满足小变形的变形条件.
1.2.3 阻尼器荷载与位移关系
初始屈服前耗能金属管各位置均处于线弹性阶段.此阶段的位移上限是耗能金属管外壁发生初始屈服,最大切应变和切应力均发生在耗能金属管外表面.应力、应变分布见图4.图中,τin、γin分别为耗能金属管内表面切应力和切应变;τout、γout分别为耗能金属管外表面切应力和切应变.
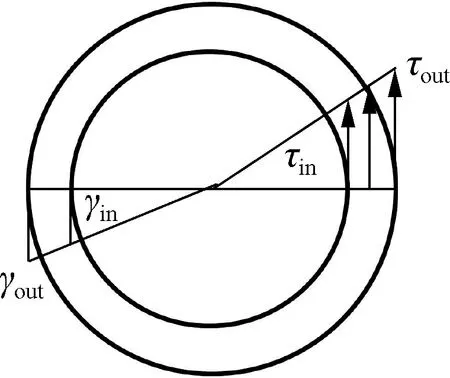
图4 耗能金属管应力、应变分布图
由图4可知,切应力、切应变满足如下关系:
τmax=τout≤τy
(5)
γmax=γout≤γy
(6)
式中,τmax、γmax分别为钢管横截面切应力和切应变的最大值.
根据材料力学理论可知,内力扭矩为
(7)
(8)
(9)
则外荷载值为
(10)
式中,ρ为耗能金属管的横截面上任意点距圆心的距离.
在线弹性阶段,假定耗能金属管横截面始终保持为平面并且与其轴线垂直,满足剪切胡克定律.位移加载上限为
(11)
荷载-位移关系式为
(12)
当δ≤δy,out时,有
(13)
式中,δy,out为耗能金属管外壁屈服时的加载位移.
综上可知,阻尼器的理论模型初始刚度和初始屈服荷载分别为
(14)
(15)
本试验共设计6种阻尼器工况(见表1).试验过程中通过改变材质和壁厚,研究不同变形条件下阻尼器的力学性能.阻尼器转动力臂长152 mm,转动力臂约束端轴孔直径和转动轴承直径均为50 mm,金属管法兰内径为52 mm,法兰外径为120 mm.选用Q345级钢和铝合金管作为耗能材料,金属管均采用国标无缝金属管,其尺寸及具体工况设置见表1.表中,tp为金属管厚度.

表1 阻尼器主要参数
2 加载试验及结果
2.1 材料性能
参照规范[11],从金属管壁取材,加工成矩形截面的标准试样.试样尺寸见图5.
采用SHIMADZU电液伺服万能试验机进行加载.为确保测得的材料力学性能的准确性,选取3个厚度为1 mm的Q345级钢标准试件进行材料拉伸试验.由于2、3 mm厚铝合金管材质相同,故Al-6063A铝合金仅取厚度为2 mm的3个标准试件进行拉伸试验.标准试件实测结果接近,取其平均值.材料力学性能指标见表2.

图5 材料试样尺寸(单位:mm)

表2 材料力学性能
2.2 加载装置及加载制度
阻尼器通过约束装置底板与大刚度工字钢梁连接固定于加载装置底部,其上部通过加载控件及传力导向杆与电液伺服试验机的作动器连接,作动器的最大承载力为500 kN,最大位移为±75 mm.试验过程中作动器加载中心线、传力导向杆轴线、加载控件中心线与转动力臂长孔中心线重合,以确保加载控件仅产生铅垂向位移.作动器施加低周往复荷载,推动加载控件进行上、下往复运动,进而通过转动力臂带动耗能金属管发生变形,并进行屈服耗能.加载装置如图6所示.

图6 加载装置示意图
试验过程中,利用试验装置自行配置的力传感器和位移传感器进行力和位移量测.采用位移控制的加载模式,加载制度见图7.初始加载幅值为5 mm,加载幅值增量为5 mm,每个加载幅值往复循环加载2周,加载速率为0.5 mm/s.每级加载完成后停止加载,观察阻尼器破坏现象并完成拍照,然后继续加载.鉴于阻尼器尺寸及加载装置原因,无论阻尼器是否发生破坏,最大位移均加载至40 mm以内,以确保转动轴承未参与承载,并免于加载力臂与约束底板间碰撞.

图7 加载制度
2.3 滞回曲线分析
本文采用等能量作图法确定阻尼器屈服点,骨架曲线上荷载下降至峰值荷载85%时对应的点即为极限荷载点.延性系数是反应阻尼器塑性变形能力的重要指标,其值取为极限荷载点与屈服荷载点对应位移的比值.各工况下阻尼器的主要力学性能指标见表3.

表3 阻尼器性能
对于Q345级耗能钢管,阻尼器BST-S-1和PT-S-1的滞回曲线见图8(a).由图可知,2个阻尼器的滞回曲线对称且光滑饱满近似于弓形,存在轻微的捏拢现象.相较于阻尼器BST-S-1,阻尼器PT-S-1的滞回曲线更加饱满,对应不同加载阶段的荷载值更高,峰值荷载提高了6.9%,但两者的屈服荷载和屈服位移相差不大.阻尼器PT-S-1的初始刚度高于BST-S-1,提高幅度为10.9%,作为耗能装置更有助于提升结构的抗侧初始刚度.通过对比纯扭转及弯-剪-扭组合变形条件下的阻尼器延性系数可知,纯扭转条件下的阻尼器PT-S-1明显高于弯-剪-扭组合变形条件下的阻尼器BST-S-1,延性系数提高了31.2%.
阻尼器BST-L-2和PT-L-2以及阻尼器BST-L-3和PT-L-3的滞回曲线分别见图8(b)和(c).由图可知,相较于阻尼器 BST-L-2和BST-L-3,纯扭转条件下的阻尼器PT-L-2和PT-L-3在不同加载阶段的荷载值均有不同程度的提高,屈服荷载分别提高10.3%和8.1%;峰值荷载提高幅度更加明显,分别提高16.3%和10.1%.纯扭转条件下的阻尼器PT-L-2和PT-L-3的延性系数明显高于弯-剪-扭组合变形条件下的阻尼器BST-L-2和BST-L-3.阻尼器PT-L-2的延性系数较阻尼器BT-L-2提高26.9%.阻尼器PT-L-3由于加载至最大位移40 mm时荷载值仍未下降至85% 峰值荷载之下,而其屈服位移低于阻尼器BST-L-3,故相较于BST-L-3的延性系数提高幅度更加明显.
(a) BST-S-1和PT-S-1

(b) BST-L-2和PT-L-2

(c) BST-L-3和PT-L-3
通过对比不同壁厚的耗能铝合金管的滞回曲线可知,随着管壁厚度的增加,阻尼器各加载阶段的荷载值均有不同程度的提升,延性性能更佳,滞回曲线更加饱满,具有更强的耗能能力.此外,弯-剪-扭组合变形条件下阻尼器的强度退化进程更快.以阻尼器PT-S-2和BST-S-2为例,位移达到30 mm时,前者在加载第1周时并未出现显著的强度退化,后者则已发生明显的强度退化现象.
采用所提的阻尼器力学模型,可计算得到阻尼器的理论初始刚度和屈服荷载.计算值与试验值对比见表4.由表可知,试验所得的初始刚度和屈服荷载与理论值存在一定的差异,误差分别为6.2%~17.9%和15.2%~17.2%.究其原因在于:①理论分析中,以金属管外径对应圆柱面材料屈服作为阻尼器屈服的判定标准,这与试验通过等能量法得到的屈服荷载获取方式存在差异;②试验过程中各部位的连接并非完全固结,且存在加工误差.

表4 理论值与试验值对比
3 新型阻尼器数值仿真
3.1 数值模型的建立
基于ABAQUS有限元软件建立阻尼器有限元模型,采用ABAQUS/Standard分析模块.耗能金属管采用壳单元S4R进行模拟,其余部件均采用三维八节点减缩积分单元C3D8R进行模拟.所有部件的材料模型均采用双线性随动强化模型,根据阻尼器的材性试验确定金属管单轴应力-应变关系的主要参数.加载控件与2个转动力臂采用铰接的连接方式,以模拟转动效应.考虑到试验过程中约束装置仅起到限制阻尼器运动的作用,故模拟过程中未考虑螺栓连接,而是将约束装置作为整体进行建模,耗能金属管法兰分别与转动力臂和约束装置侧板通过Tie命令进行绑定.加载控件采用刚体耦合参考点法连接,荷载施加于参考点之上,并采用非线性静力分析方法进行模拟,加载制度与试验保持一致.
3.2 结果分析
阻尼器BST-L-1和PT-L-1的模拟结果和试验结果对比见图9.由图可知,模拟的滞回曲线形状及数值整体上与试验结果吻合良好.

(a) 弯-剪-扭组合变形

(b) 纯扭转变形
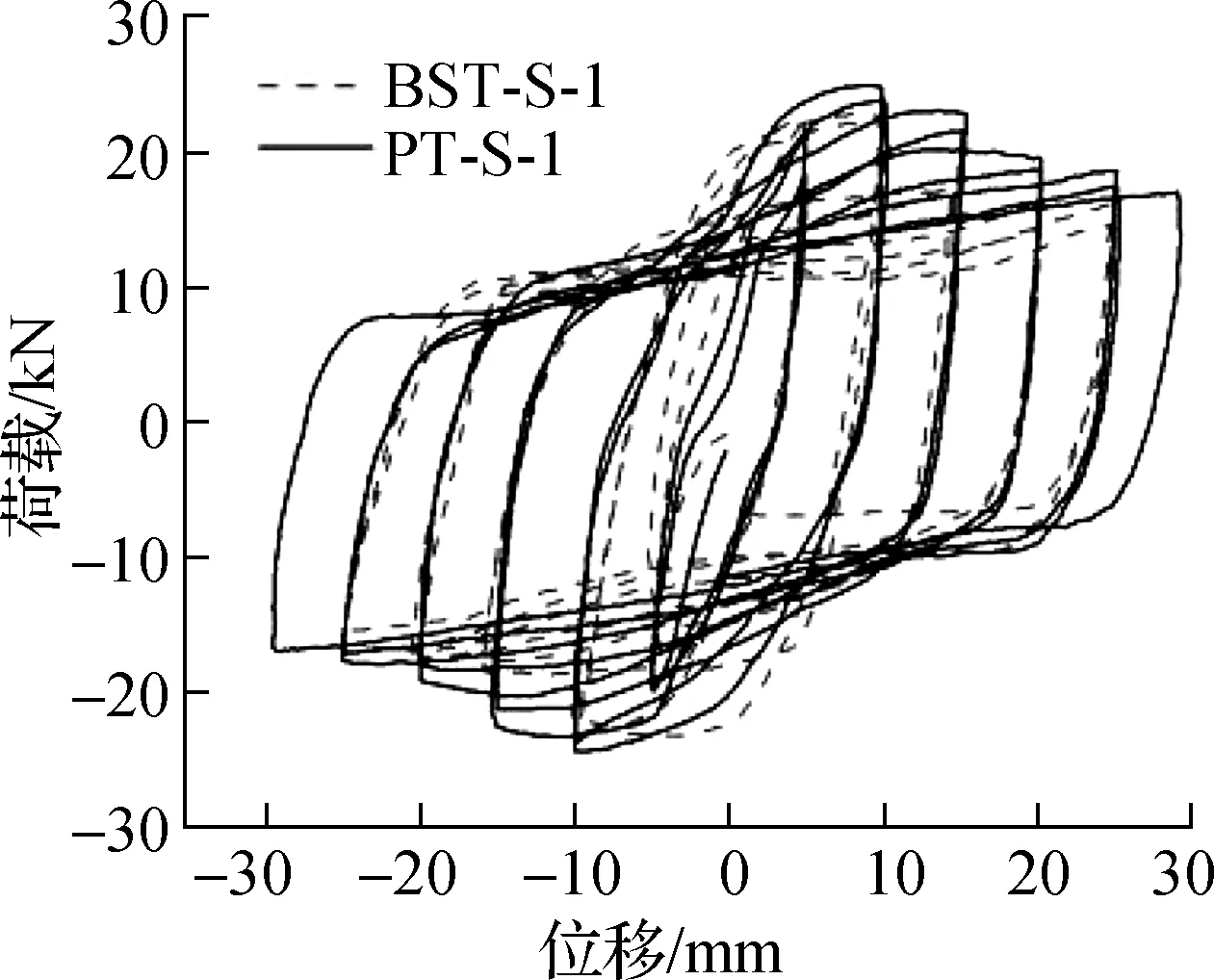
由于纯扭转变形阻尼器的力学性能更佳,故本文仅给出了数值模拟得到的阻尼器PT-S-1的耗能钢管Von-Mises等效应力云图,其与试验金属管变形对比情况见图10.由图可知,加载至位移幅值δ=15 mm时,整根钢管外部氧化皮层均出现剥离,钢管中部出现明显的凹凸鼓曲,发生轻微屈曲现象,多数截面发生屈服.随着加载位移幅值的增加,钢管屈曲区域逐渐向钢管两端扩展.δ=20 mm时,钢管中部发生严重屈曲变形,部分区域出现明显的扭曲畸变现象,此时钢管大部区域已完全屈服并退出工作状态,荷载明显下降.随着加载位移幅值的进一步增加,δ=25 mm时,为更清晰观察钢管变形情况,对钢管进行擦拭,此时整根钢管外表面多处于剪切屈服状态,应力、应变分布均匀.通过分析循环加载作用下耗能钢管的屈曲变形过程可知,耗能钢管的屈曲模态为多波高阶屈曲.该屈曲现象是一种较为理想的屈曲模式,有利于提高钢管的耗能能力.通过对比可知,模拟分析得到的钢管破坏现象与试验破坏现象基本一致.

(a) δ=15 mm试验现象

(b) δ=20 mm试验现象

(c) δ=25 mm试验现象
(d) δ=15 mm模拟结果
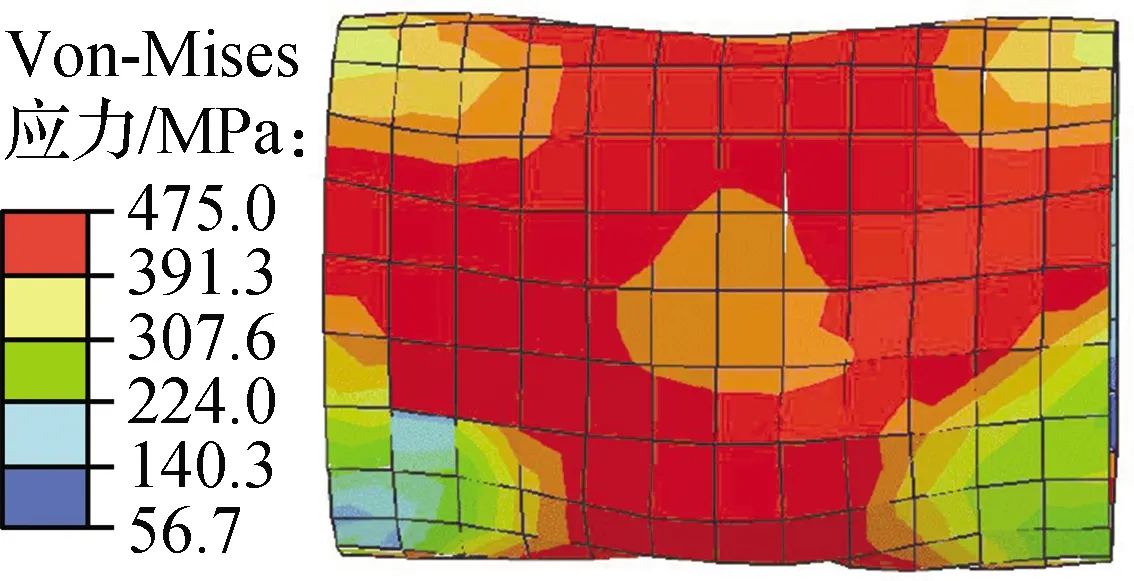
(e) δ=20 mm模拟结果
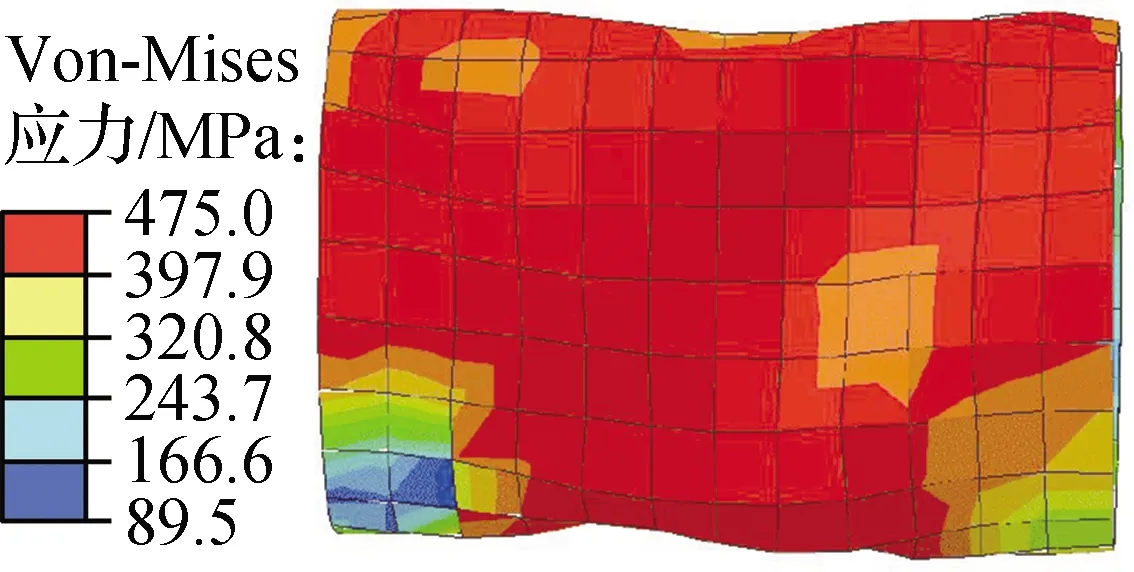
(f) δ=25 mm模拟结果
4 钢框架支撑结构抗震性能分析
4.1 Y形支撑设计
采用文献[12]中的5层Y形偏心支撑钢框架进行抗震性能研究.该支撑结构层高均为3.0 m,跨度为6.0 m.结构的平面、立面布置见图11,阻尼器布置情况见图12.该结构所在地区抗震设防烈度为8度,设计地震基本加速度为0.2g,建筑场地类型为Ⅱ类,设计地震分组为第1组.本文选取其中一榀作为研究对象,共设计了3种分析工况.工况1、2、3分别为纯钢框架结构、设置剪切屈服型和纯扭转屈服型耗能梁段支撑结构,其中剪切屈服型耗能梁段的截面形状、尺寸和材料均与文献[12]完全相同.为比较2种耗能机制在Y形支撑结构中的减震效果,2种耗能梁段采用等屈服强度的设计原则,即耗能梁段屈服力相等,通过改变钢管数量及厚度使纯扭转屈服型耗能梁段的屈服荷载与剪切屈服型耗能梁段保持一致.

(a) 立面图

(b) 平面图

(b) 单支扭转阻尼器
(c) 剪切型阻尼器
根据结构建筑场地类别和抗震设防烈度,选择文献[13]中的5条典型地震波(编号为1#~5#),对结构进行动力时程分析.将地震波峰值加速度(PGA)分别调幅至0.2g和0.4g,对结构进行中震和大震作用下的抗震性能分析,研究不同变形耗能机制对结构抗震性能的影响.
基于ABAQUS软件建立多尺度支撑钢框架结构模型.耗能梁段、支撑平台段、阻尼器和框架梁与阻尼器连接区域均采用精细化实体单元建模,材料、单元均与3.1节中的阻尼器数值模型相同,钢框架梁柱单元采用非线性梁单元,梁单元采用iFiberLUT子程序模拟[14],支撑采用桁架单元.扭转阻尼器通过约束装置固结于支撑平台段,其转动力臂铰接于上部水平梁段实体区域(见图12(a)).
4.2 抗震性能分析
以1#和4#地震波为例,其Y形支撑钢框架的最大层间位移角见图13.由图可知,扭转型和剪切型耗能梁端均能起到较好的减震效果.中震作用下输入4#地震波时,相较于工况1,工况2和工况3的结构最大层间位移角分别降低约74.7%和 87.4%,扭转型耗能梁段减震效果明显优于剪切型耗能梁段,其余各条地震波作用下减震效果差异不大.大震作用下,工况3相较于工况2的减震效果进一步增强,1#地震波作用下减震效果最为显著,工况2和工况3相较于工况1的最大层间位移角分别降低约78.6%和93.5%,但3#地震波作用下扭转型耗能梁段减震效果则略有降低.
通过对比5条地震波作用下得到的各工况结构最大层间位移角均值可知,对比中震而言,大震作用下扭转型耗能梁段的减震效果更为显著,中震作用下工况2和工况3相较于工况1的最大层间位移角均值分别降低约78.6%和81.3%,减震率仅相差2.7%左右;大震作用下最大层间位移角均值分别降低约79.6%和86.7%,相较于剪切型耗能梁段,扭转型耗能梁段减震率提高约7.1%,具有更加显著的减震效果.究其原因在于,大震作用下扭转型阻尼器的耗能钢管屈服区域更加分散,应力、应变分布更加均匀,相较于剪切型阻尼器其耗能能力显著提高,进而提升了其对结构的减震效果.

(a) 中震结果

(b) 大震结果
图14给出了5条地震波作用下各工况结构的顶点位移最大值及不同工况下顶点位移最大值的平均值.由图可知,工况2和工况3的减震效果明显优于工况1.中震作用下输入4#地震波时,工况2和工况3的结构顶点位移最大值相较于工况1分别降低约72.4%和86.4%,顶点位移最大值减震率差值高达12.0%,输入其余各条地震波时顶点位移最大值减震效果差异不大.相较于工况1,中震作用下5条地震波在工况2和工况3的结构顶点位移最大值的平均值分别降低约76.7%和79.6%,耗能梁段减震效果差异不大.
大震作用下,除3#地震波外,其余地震波下工况3的顶点位移最大值降幅均高于工况2,且1#地震波下两者差异最为显著,此时工况2和工况3较工况1的结构顶点位移最大值分别降低约77.3%和93.0%.对于各地震波作用下结构顶点位移最大值的平均值而言,工况2和工况3较工况1分别降低约78.9%和85.7%.由此可知,相较于剪切型耗能梁段,扭转型耗能梁段支撑结构顶点位移最大值降低幅度提高约6.8%.综合中震和大震作用下结构顶点位移数据变化情况可知,随着地震动强度的增加,扭转型耗能梁段的减震性能更优于剪切型耗能梁段.

(a) 中震结果

(b) 大震结果
5 结论
1)通过试验研究了不同材料及壁厚的金属阻尼器的力学性能.结果表明,纯扭转条件下阻尼器的力学性能更优,滞回曲线更饱满,承载力及耗能能力更强.
2)基于试验结果进行理论分析,建立了初始屈服前阻尼器的力学模型,并计算其初始刚度和屈服荷载.理论分析结果与试验结果基本吻合,从而验证了其力学模型的准确性.
3)采用本文选取的材料本构模型和接触、约束类型,建立了阻尼器有限元模型.该模型能够模拟阻尼器的力学性能.
4)将提出的新型扭转型耗能梁段与传统剪切型耗能梁段分别应用于Y形支撑钢框架,进行非线性动力时程分析.结果表明,本文提出的新型扭转阻尼器减震性能更佳.

