低截获MIMO雷达改进MUSIC算法

赵筱彤, 周建江

(南京航空航天大学雷达成像与微波光子学教育部重点实验室, 江苏 南京 211106)

0 引 言

随着信息技术的发展,单部雷达已经不能满足复杂战场环境的需求,多部雷达协同工作成为了必然的发展趋势[1]。学者们结合了无线通信系统中多输入多输出(multiple input multiple output,MIMO)的概念以及综合脉冲孔径雷达 (synthetic impulse and aperture radar, SIAR)技术,在2004年IEEE雷达会议上正式提出了MIMO雷达[2]。随着对MIMO雷达的深入研究,将MIMO雷达分为共址MIMO雷达和统计MIMO雷达[3]。本文选取单基地共址MIMO雷达进行研究,其在接收端采用匹配滤波方式,产生虚拟阵列孔径,相当于扩大了阵元数目,使得空间分辨增益以及角度分辨力都得到了提高[4]。近年来利用MIMO雷达进行目标定位[5]受到广泛的关注,现有的MIMO雷达多信号分类(multiple signal classification,MUSIC)算法大多是针对平稳信号进行研究[6]。但是在军事领域中,机载雷达的探测对象为机动目标,其运动会产生多普勒效应,故接收信号为非平稳信号。

MUSIC算法自1979年的Schmidt创立开始,一直在创新和改进[7-8],时至今日，仍有很多学者致力于MUSIC算法的研究[9]。针对非平稳信号的MUSIC算法,一般采用时频分析[10]。现有的MIMO雷达时频MUSIC算法仅仅是利用空间时频分布(spatial time frequency distribution, STFD)矩阵代替接收信号的协方差矩阵,完成对非平稳信号的处理[11-12]。本文在此基础上对非均匀线阵单基地MIMO雷达展开降维预处理,降低算法运算量,同时参考盲源分离技术[13],通过白化处理、时频分析、时频点筛选、正交联合对角化以及Givens旋转等信号处理,对MIMO雷达时频MUSIC算法进行改进,提高算法的估计精度,降低算法的均方根误差(root mean squared error, RMSE),使算法具有低信噪比(signal to noise ratio,SNR)、低快拍数的优势。

在电子对抗战中,随着电子侦察技术的快速发展,必须要提高雷达的生存能力。雷达在保证精确探测到远方弱小目标的同时,还要防止被侦察设备、反辐射导弹截获[14]。因此雷达工作的SNR环境通常较低,而现有的MIMO雷达时频MUSIC算法所适用的最低SNR多为0 dB左右[15],而仿真实验证明本文提出的改进MUSIC算法将SNR降低至-2 dB,验证了MIMO雷达使用本文改进MUSIC算法进行角度估计时,具有低截获性能。

1 MIMO雷达非平稳信号模型

MIMO雷达自身具有宽发窄收的特点,具有较好的反侦察、低截获能力[16]。针对测向MIMO雷达,发射天线阵元间距增大有助于支持目标方面的空间分集,而分集会导致目标分量在接收信号中更有利的分布[17]。同时,综合考虑MIMO雷达的发射和接收阵,使其可以在小规模阵列条件下实现更高的角度分辨率。本文参考文献[18]中分布式发射和密布式接收的MIMO阵列,此阵列可以有效抑制目标闪烁,同时实现波达方向估计。

考虑到单基地MIMO雷达系统的特点[19]以及本文研究的目的,采用图1所示单基地MIMO雷达系统模型。假设发射天线为M个阵元组成的非均匀线阵,接收天线为N个阵元组成的均匀线阵,线阵布阵方式如图1所示。考虑到资源利用率问题,发射阵列中前(k+1)个阵元排布与接收阵列完全一致,为阵元间距d的密布式阵列,故接收阵列阵元数N=k+1;而后(k-1)个阵元为了达到抑制目标闪烁,提高角度估计精度的目的,本文将发射天线间距扩大为(k+1)d,故整个发射阵列阵元数M=2k。图1中阵元间距d=λ/2,λ为信号波长。

假设图1中的探测目标共有Q个,第q个目标的探测角度为θq,且目标相对于雷达满足远场条件。因此接收信号的矩阵形式[20]如下所示:

(1)

式中：取快拍数为L,则t=1,2,…,L。S(t)=[S1(t),S2(t),…,SM(t)]为天线发射信号矢量,根据MIMO雷达的特点,SmSmH=I,w(t)为均值为0的高斯白噪声。

机动目标运动速度的变化会产生多普勒频移,所以目标的回波信号为非平稳信号。故bq(t)=βqexp{j2π(fqt+(μq/2)t2)} 为第q个目标的散射信号,其中βq为第q个目标的雷达散射截面积(radar cross section, RCS)的复振幅,fq和μq为第q个目标的多普勒频移和调频斜率。将式(1)中的发射天线导向矢量at(θq)和接收天线的导向矢量ar(θq)分别记为

at(θq)=[at1(θq);at2(θq)]=
[1,e-j2π(d/λ)sin θq，…，e-j2π(k(d/λ)sin θq，
e-j2πk(k+k+1)(d/λ)sinθq，…，e-j2π(M-1)(d/λ)sin θq]T

(2)

ar(θq)=[1,e-j2π(d/λ)sin θq，…，e-j2π(N-1)(d/λ)sin θq]T

(3)

MIMO雷达在信号处理的过程中,在接收阵列处设置M个匹配滤波器,对接收信号进行一维时域匹配滤波,形成MN个虚拟阵列[21]。滤波后的信号y(t)如下所示：

y(t)=A(θ)b(t)+W(t)

(4)

L个快拍下的y(t)形成矩阵Y,如下所示:

Y=AB+W

(5)

式中：Y=[y(1),y(2),…,y(L)]为MN×L维信号矩阵;A(θ)=[a1(θ1),a2(θ2),…,aq(θq)]为MN×Q维的虚拟阵列联合导向矩阵,其中aq(θq)=at(θq)⊗ar(θq)是由发射天线导向矢量at(θq)与接收天线导向矢量ar(θq)进行Kronecker积运算得到的;矩阵W为MN×L维、均值为0、方差为δ2的高斯白噪声矩阵;B=[b(1),b(2),…,b(L)]为Q×L维散射系数,其中b(t)的表达式如下所示:

(6)

2 MIMO雷达改进MUSIC算法

2.1 非均匀阵列MIMO雷达降维预处理

通过文献[22]的研究可知,当发射线阵与接收线阵均为阵元间距是半波长的均匀阵列时,有效的虚拟阵元数目为发射阵元数与接收阵元数的和减1。由图1可知,本文采用的单基地MIMO雷达非均匀发射线阵的前(k+1)个阵元是间距为d的均匀线阵,而后(k-1)个阵元可视为每间隔(k+1)个间距为d的阵元取一个作为发射阵元。结合空间卷积原理[23],该模型的有效虚拟阵元数目中发射阵元数可以理解为是发射阵列中工作和未工作的,即范围内所有阵元数目为(2k+1)+(k+1)(k-2)+1。由于接收线阵为均匀阵列,因此该模型有效虚拟阵元数是

Ne=[(2k+1)+(k+1)(k-2)+1]+N-1=
k2+k+N-1

(7)

这种方法填补了非均匀发射线阵中阵元间距大于半波长的部分。根据有效虚拟阵元数目Ne,可将MN×1维的导向矢量a(θ)通过线性变换为g(θ)=[1,ejπ sin θ,…,ejπ(Ne-1)sin θ]T即Ne×1维的导向矢量,线性变换过程如下所示:

a(θ)=at(θ)⊗ar(θ)=Fg(θ)

(8)

由于非均匀发射阵列具有前半部分和后半部分均为均匀线阵的特点,因此针对这一特殊性,将变换矩阵F调整为

F=[F1;F2]

(9)

式中：F1是针对发射线阵中前(k+1)段均匀阵列的变换矩阵；F2是针对后(k-1)段均匀阵列的变换矩阵,表达式为

(10)

(11)

因此,F1、F2组成了MN×Ne维的变换矩阵F。根据式(8)将导向矩阵A变为

A=FG

(12)

其中,虚拟线阵的导向矢量矩阵G=[g(θ1),g(θ2),…,g(θq)],将式(12)代代入式(1)中,得到

X=FGBS+W

(13)

由式(13)可以看出,信号位于由G构成的低维空间之中,因此,可以将信号转换为低维信号。由于目标信息保留在转换后的低维信号中,还可以在低维空间中进行角度估计,降低了算法的运算量。假设一个Ne×MN维的降维变换矩阵D,则式(13)转变为

XD=DFGBS+DW

(14)

为了保证降维处理后的噪声仍是均值为0、方差为δ2的高斯白噪声,变换矩阵就必须满足DDH=INe,因此,变换矩阵D为

(15)

对匹配滤波处理之后的接收信号Y,也进行相应的降维处理,得到低维空间下的匹配信号Z,其表达式如下:

Z=DY

(16)

通过以上所述,将MN×L维矩阵Y变换为Ne×L维矩阵Z。降低了信号的维度空间,同时保留了目标探测信息。这种针对非均匀阵列的降维操作不仅仅大大降低了运算量,还不影响后续的MUSIC算法。

2.2 白化处理

正常情况下,雷达获取数据都具有一定的相关性[24],本文采用白化处理方式降低信号之间的相关性,提高信号的收敛性[25],为后续时频分析中时频点的筛选以及低SNR下的MUSIC算法提供了更高的精度。

降维处理后接收信号Z(t)的自相关函数为

(17)

如果没有噪声,处理后信号Z(t)的自相关函数为

RD=(DAB)(DAB)H

(18)

因此,由式(17)和式(18)可得

(DAB)(DAB)H=RZ-δ2I

(19)

假设对应的白化矩阵为W,定义为WRDWH=W(DAB)·(DAB)HWH=I,结合酉矩阵定义UUH=I,即可得

DAB=W#U

(20)

上式中W#为W的摩尔-彭若斯广义逆矩阵,将式(20)代入式(19)得

(21)

令K=diag[(λ1-δ2)1/2,(λ2-δ2)1/2,…,(λNe-δ2)1/2],那么W#=UK,进而可以得到白化矩阵W的表达式为

W=K-1UH

(22)

因此,可以得到白化处理后的信号H为

H=WZ

(23)

2.3 基于WVD的STFD矩阵

WVD是一种二次型时频分布的方式[26]。信号矢量H(t)基于WVD分布的STFD矩阵[27]表达式如下:

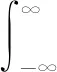
(24)

式中的STFD矩阵是由信号自身的时频分布矩阵和信号之间的时频分布矩阵组成的,分别称为自项和交叉项。由于信号矩阵H(t)中包含Ne个信号信息,因此会产生交叉项。假设Ne=2,即H=[H1;H2],那么其相应的STFD矩阵为

(25)

其中,主对角线元素对应的是非平稳信号自身时频点的WVD分布结果,而其他部分元素对应的则是非平稳信号间形成时频点的WVD分布结果。

(26)

由于自项与矩阵范数之间的比率在0～1之间,因此设置阈值如下：

(27)

通过现有知识[28]大量仿真得到,当ζ>0.1时,可判定该时频点为自项点。

2.4 正交联合对角化处理

时频分析中筛选出来的n个时频点所对应的STFD矩阵按列串联为一组复矩阵Rjd=[DH1;DH2;…;DHn],本文采用基于Givens旋转的正交联合对角化[29]的方法,来计算复矩阵的近似实值公共正交基。由联合对角化原理可知,联合矩阵具有如下性质:

Rjd=VCVH

(28)

式中：C=[C1;C2;…;Cn]是拟对角矩阵级联；V是正交矩阵。因此式(28)可以拆分为Rjd1=VC1VH,…,Rjdn=VCnVH。该算法的目的是通过迭代运算找到一个正交矩阵V使得矩阵C尽可能是对角阵,且与矩阵Rjd共有一种“平均特征结构”。式(28)等价于求解约束最大化问题:

(29)

本文对每一个STFD矩阵进行Givens旋转,令c2+s2=1,其中c=cos(θ),s=sin(θ),θ为旋转角度,旋转矩阵如下:

(30)

由式(30)可知,通过对n个STFD矩阵的一系列Givens旋转迭代运算,即可实现对该矩阵组的正交联合对角化,所有Givens旋转矩阵的乘积即是联合对角化矩阵V,迭代收敛时最后一步的C,即为最优对角阵组。

由于V中含有信号子空间和噪声子空间全部的信息,因此,直接利用V和C进行空间谱估计。通过对角阵列C中的每一组对角矩阵得到矩阵的联合特征值,而后找到对应的特征向量UN,最终改进MUSIC算法的空间谱函数为

(31)

综合本节内容,本文所提出的MIMO雷达改进MUSIC算法信号处理流程,如图2所示:

3 MIMO雷达射频隐身技术

机载雷达在电子战中通常采用射频隐身技术来对雷达进行保护。因此,提高MIMO雷达的射频隐身能力,对抗截获接收机是本文研究MIMO雷达改进MUSIC算法的主要目的。

由雷达距离方程可以得到,MIMO雷达最大截获距离为

(32)

式中：GT和GR为发射和接收天线增益；M是阵列数目；PT为雷达发射功率；η为信号占空比；tB为信号驻留时间；δ为目标RCS；N0为雷达接收机处的噪声功率谱密度；SNRmin为雷达间最小可探测SNR。由于第3节对MIMO雷达接收信号进行了相关的信号处理,故式(32)中阵列数目M为第2.1节中有效虚拟阵元数目Ne。

射频隐身技术中用施里海尔截获因子衡量雷达的射频隐身性能,施里海尔截获因子定义为截获接收机最大截获距离与雷达最大探测距离之比。结合式(32)通过推导,可以得到下式所示的MIMO雷达截获因子表达式:

(33)

式中：Gi是截获接收机天线增益；γ∈(0,1)为非相参积累损失,本文中令Ni与N0相等；Bi为截获接收机带宽；SNRr,min为雷达最小可检测信噪比；SNRi,min为截获接收机最小可检测SNR,∑(θ)为雷达在截获接收机方向归一化方向图因子。

由文献[30]可知,雷达的功率域被截获概率为

p=1-e-0.5α

(34)

由式 (33)可知,MIMO雷达的射频隐身能力受到信号发射功率PT和驻留时间tB的影响。首先在环境参数确定的情况下,SNR与发射功率PT成正比,即SNR越小,PT就越小,相应的α就越小,p就越小,雷达射频隐身能力就越好;其次由文献[31]可知,信号驻留时间tB与快拍数L成正比,即L越小,tB越小,相应的α就越小,p就越小,雷达射频隐身能力就越好。

4 仿真实验

仿真实验模拟在某一时刻单基地MIMO雷达探测运动目标方位角度的场景。雷达模型和图1所示，模型是发射阵列为分布式线阵、接收阵列为密布式线阵的单基地MIMO雷达,令k=4,则M=8,N=5,式(7)中的有效虚拟阵列Ne=24,阵元间距d为半波长。假设有3个运动目标,在某一时刻散射信号起止频率分别为fs1=0.12、fe1=0.32、fs2=0.15、fe2=0.35、fs3=0.18、fe3=0.38。

本文共设计3组实验,通过第1节中介绍的MIMO雷达时频MUSIC算法与本文改进MUSIC算法对比实验的方式,分析两种算法的探测性能、临近角度分辨能力以及射频隐身能力。

4.1 实验1 (探测性能对比)

假设3个运动目标回波信号到达角分别为θ1=-10°、θ2=3°、θ3=10°,快拍数L为100,SNR为10 dB。MIMO雷达时频MUSIC算法与本文改进MUSIC算法对比仿真实验结果如图3所示。图3中,MIMO雷达使用两种算法均能探测出3个目标角度。图3(a)中时频MUSIC算法波峰的高度为30 dB;图3(b)中改进MUSIC算法波峰的高度为40 dB。显然,本文改进MUSIC算法的波束更为尖锐,指向精度有所提高。

4.2 实验二 (临近角度的分辨能力对比)

假设3个运动目标回波信号到达角分别为θ1=-10°,θ2=9°,θ3=10°,快拍数L为100,SNR为5 dB。MIMO雷达时频MUSIC算法与本文改进MUSIC算法对比仿真实验结果如图4所示。

仿真目标2和目标3的角度相差仅为1°,图4(a)中目标2、目标3探测角度重合,探测角度为9.5°,无法分辨;图4(b)中探测角度为9°、10°,可以分辨出临近目标,证明了本文提出的改进MUSIC算法具有较好的分辨能力。

4.3 实验3 (射频隐身性能对比)

通过第4节的分析可知,SNR和快拍数越小,射频隐身性能就越好。因此实验3仿真两种MUSIC算法的估计精度随着SNR和快拍数的变化过程,并且证明了本文算法的低截获性能。

本文采用RMSE来衡量两种MUSIC算法的估计精度。利用蒙特卡罗实验使仿真过程趋近于真实过程。基于蒙特卡罗实验的RMSE表达式如下所示:

(35)

式中,Q为目标数目；P为蒙特卡罗次数,本次实验选取蒙特卡罗数为P=200。

假设3个运动目标,其信号到达角分别为θ1=-10°、θ2=3°、θ3=10°、SNR=5 dB。两种MUSIC算法RMSE随快拍数L变化的对比仿真实验结果如图5所示。

由图5可见,当快拍数低于80时,本文提出的MIMO雷达改进MUSIC算法的RMSE低于时频MUSIC算法,证明改进MUSIC算法在低快拍数的条件下具有较好的估计精度,同时也证明了在相同的角度估计精度下,改进MUSIC算法所需的快拍数更小,具有更好的射频隐身能力。

假设3个运动目标的信号到达角不变,快拍数L为100。两种MUSIC算法的RMSE随着SNR变化的对比仿真实验结果如图6所示,其中图6(a)为MIMO雷达时频MUSIC算法的RMSE,图6(b)为MIMO雷达本文改进MUSIC算法的RMSE。如图6所示,在SNR=-15 dB的状态下,图6(b)的估计误差比图6(a)小20°,证明在具有相同射频隐身能力时,本文改进MUSIC算法具有更好的估计精度。除此之外,当2种MUSIC算法估计精度达到最高即RMSE为0时,图6(a)中的最小SNR为0 dB,图6(b)中的最小SNR为-2 dB,证明了本文改进MUSIC算法所需的最小SNR降低了2 dB,具有更好的射频隐身能力。

功率域低截获概率技术主要是降低雷达发射机的峰值功率。设雷达与截获接收机具有相同的噪声功率谱密度,噪声温度为290 K,噪声系数为2,信号占空比为0.01,目标RCS为1 m2。参考文献[30]中雷达和截获接收机的参数。根据本文阵列排布特点,阵元数M=Ne=24,令驻留时间为26 ms,根据式(33)和式(34)得到如图7所示的雷达被截获概率随SNR变化曲线图。

图6仿真实验中两种算法估计精度最高时,所需最低SNR分别为0 dB和-2 dB,代入图7可知时频MUSIC算法的被截获概率为1.74%,而本文改进算法的被截获概率为1.55%。图6(b)中改进算法在-5 dB时,才开始有较大的估计误差,此时的被截获概率为1.31%。因此本文改进算法保证了雷达低截获性能。

5 结 论

本文提出一种低截获的MIMO雷达改进MUSIC算法。本文在解决单基地MIMO雷达非均匀阵列探测运动目标问题时,采用降维预处理、白化处理、时频分析、时频点筛选、正交联合对角化几个信号处理过程,提高了算法的估计精度以及射频隐身能力。与MIMO雷达时频MUSIC算法的对比仿真实验结果表明:① 本文提出的MIMO雷达改进MUSIC算法指向精度有所提高;② 本文改进MUSIC算法可以分辨角度差为1°的临近目标,分辨能力有所提高;③ 本文改进MUSIC算法在低SNR、低快拍数条件下估计精度更高,所适用的SNR环境降低了2 dB。本文算法的研究仅考虑了MIMO雷达对运动目标的定位问题,在后续研究中可以将算法应用在雷达对运动目标角度跟踪之中。