基于概率数据关联的雷达导引头抗速度拖引干扰算法

王 琪, 廖志忠, 燕 飞

(中国空空导弹研究院, 河南 洛阳 471009)

0 引 言

脉冲多普勒(pulse Doppler, PD)雷达是一种利用多普勒效应检测目标信息的全相参雷达,具有跟踪精度高、杂波抑制能力较强等优点,被广泛应用于目标检测、跟踪和制导。复合制导的空空/地空导弹均采用PD雷达导引头进行末制导[1]。

为了减弱脉冲多普勒雷达导引头的优势,目标通过所携带的电子干扰设备,发射多普勒欺骗信号,使雷达导引头无法测量到真实的目标多普勒信息[2]。其释放的多普勒欺骗干扰信号的主要样式包括:多普勒频率多假目标干扰、多普勒频率噪声干扰、多普勒频率闪烁干扰、速度拖引(velocity gate pull-off, VGPO)干扰等。其中最常见的欺骗干扰样式是速度拖引干扰[3],相比于真实的目标多普勒频率,拖引干扰信号的多普勒频率逐渐变大或减小,且干扰信号功率大于真实目标的回波信号功率,使雷达频率跟踪环路自动跟踪虚假的多普勒频率。速度拖引干扰信号多普勒频率按照一定规律变化,所产生的虚假速度测量信息会造成滤波航迹逐渐偏离目标真实航迹[4],雷达导引头无法精确跟踪目标,最终导致导弹脱靶量增大。数字射频存储器(digital radio frequency memory, DRFM)技术特别适用于干扰各种相参信号处理体制的雷达,由其产生的速度欺骗干扰信号与雷达导引头发射信号相干,从而干扰信号和目标信号在频率、波形、电磁散射特性等方面相去无几[5],进一步提升了干扰的灵活性和对抗难度。

针对速度拖引干扰,有效抗电子干扰措施主要基于雷达信号处理技术和雷达数据处理技术。目前,大部分抗欺骗干扰的研究都是利用信号处理的方法,而利用数据处理方法进行抗欺骗干扰的研究较少。在雷达信号处理方面，采取的抗电子干扰措施有脉冲分集[6-7]、干扰信号频谱特征分析[8-11]、干扰信号相位量化差异[12-13]、多基地雷达统计相关差异[14]、多域联合处理[15]、离散chirp-Fourier变换联合估计目标和干扰信号[16]、频域前后缘跟踪方法[17]、基于长短期记忆神经网络识别拖引干扰[18]等。但是逼真度很高的干扰信号不可能被先进的信号处理技术完全剔除,进入后续雷达数据处理单元的量测信息不可避免地包含干扰信息。在雷达数据处理方面,文献[19]提出了采用双模型方法处理雷达位置测量信息和接近速度测量信息,一个模型处理雷达位置量测,另一个模型处理雷达位置量测和接近速度量测,并假设两个模型的处理结果不相关,然后进行假设检验以分析雷达是否受到速度拖引干扰。文献[20]研究了基于速度、加速度、过载等指标的干扰目标智能识别技术,判断是否存在距离-速度同步拖引干扰,但文中并未给出判断真实目标的具体实现方法。对于距离波门拖引干扰,文献[21-23]研究了利用概率数据关联概率数据关联(probability data association, PDA)跟踪杂波和距离拖引干扰环境中的机动目标。在红外导引头抗干扰方面，PDA也得到了应用,文献[24]研究了利用PDA算法实现对红外目标和诱饵干扰的识别,可以有效解决红外干扰形成的假目标、目标遮挡等难题。文献[25]研究了基于PDA的红外弱小运动目标跟踪问题,提高了红外目标的识别与跟踪性能。文献[26]研究了杂波环境下,雷达/红外复合传感器基于多检测PDA滤波对运动目标的跟踪。

根据以上分析,对于工作于高重频波形下的PD雷达导引头,为了解决多重速度拖引干扰环境下雷达导引头的目标跟踪与制导问题,本文采用序贯扩展卡尔曼滤波(sequential extended Kalman filter, SEKF)算法处理雷达导引头角度测量信息和Doppler测量信息,并在处理Doppler信息时提出了采用PDA的方法对抗速度拖引干扰。算法建立了包含Doppler量测信息的目标状态估计模型,模型中采用PDA滤波算法，消除多重速度拖引干扰对目标状态估计值的影响。仿真结果表明,该算法能够稳定跟踪释放多重速度拖引干扰的目标,有效抑制速度拖引干扰对导弹制导系统的影响,提高系统的制导精度。

1 带Doppler量测的制导信息滤波模型

采用高重频波形的弹载PD雷达导引头除可以提供角度量测信息外,还可以提供Doppler量测信息,利用Doppler信息可以有效提高目标的跟踪精度。为解决带Doppler量测信息的目标状态估计问题,可以利用斜距估值和Doppler量测的乘积构造伪量测信息,对于角度量测和此伪量测信息采用序贯SEKF算法,序贯处理这两类量测信息[27-28]。

制导信息滤波模型由状态方程和量测方程组成[29]。在笛卡尔坐标系中,制导信息估计状态方程为

xk+1=Φxk+Guk+Γwk

(1)

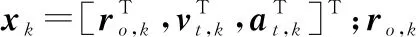
系数矩阵为

(2)

(3)

(4)

雷达导引头可以测量出导弹-目标视线在惯性坐标系中的俯仰角φy和方位角φz,则对于导引头角度测量信息,量测方程为

(5)

(6)

对于Doppler测量信息,可以根据雷达载波频率等价转换为接近速度测量信息,k时刻接近速度vc,k定义为

(7)

由式(6)、式(7)可以看出,接近速度vc,k与状态向量xk是强非线性关系[31]。为了减弱Doppler量测和目标运动状态向量之间的强非线性,可采用如下的伪量测转换方程[32-33]:

(8)

(9)

文献[27,33]给出了转换量测误差前两阶矩的一致性估计证明。利用式(1)的状态方程和式(6)、式(9)的角度量测方程和接近速度伪量测方程,既可完成对目标运动状态的序贯滤波估计,主要计算步骤如下。

步骤 1时间更新滤波估计:

(10)

步骤 2角度量测更新滤波估计

(11)

步骤 3伪量测更新滤波估计

(12)

步骤 4最终滤波估计

(13)

2 PDA抗速度拖引干扰算法

PDA滤波算法适用于杂波环境中单个目标的跟踪,其依据目标运动信息,计算各个量测信息与航迹的匹配程度,并以此生成一个新的量测值来更新航迹。

空空/地空导弹末制导飞行过程属于单目标跟踪过程,即在作战空域中仅跟踪制导一个目标,这一点满足PDA理论的基本假设。在多重速度拖引干扰环境下,由于干扰因素的存在,在任意时刻,导引头测量信息中存在多个有效回波。PDA理论认为所有量测信息都有可能源于所跟踪的目标,只是每个量测信息源于目标的概率不同。

文献[31]中给出了PDA理论的基本描述,引述如下。定义以下符号及所表示的含义[31]:

Zk={zk,1,zk,2,…,zk,mk}:表示导引头在k时刻的确认量测集合;

zk,i:表示k时刻导引头接收到的第i个量测;

mk:表示k时刻确认量测个数;

Zk={Z1,Z2,…,Zk}:表示直到时刻k的累计确认量测集;

再令

(14)

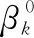
(15)

(16)

(17)

式中：

(18)

其中，λ为干扰杂波的空间密度；PD为目标检测概率；PG为正确量测落入跟踪门的概率；Sk为量测新息的协方差。关于PDA算法的详细推导及收敛性分析详见文献[34-36]。

在多重速度干扰环境下,干扰信号和目标信号均源自同一飞行平台,角度测量信息源自同一目标,因此角度测量信息无需进行PDA滤波。在角度通道滤波后序贯处理接近速度量测信息时引入了PDA滤波,利用PDA滤波计算每个接近速度量测信息与角度通道滤波给出的接近速度估值的关联概率,可以利用此关联概率抑制速度拖引干扰对目标状态估计的影响。

此时Sk取接近速度伪量测新息的方差,按下式计算:

(19)

(20)

(21)

从而目标状态估计可表达为

(22)

(23)

(24)

式中：

(25)

3 数字仿真验证

图1所示为采用最优导引律的导弹制导系统模型[29]。

制导信息估计环节用于估计目标状态信息,包括弹目相对距离、目标速度、目标加速度等,这些信息作为最优导引律的输入用于计算导弹控制加速度。速度拖引干扰会影响导弹对目标信息的估计准确性,从而影响导弹制导精度;也会导致雷达导引头速度门中心偏离真实目标,造成导引头丢失目标。

下面给出数值仿真验证结果。仿真中假设导弹和目标在同一水平面内飞行,仿真初始条件如表1所示。

表1 仿真初始条件

雷达导引头测角、测速噪声以及PDA滤波器参数见表2。

表2 仿真参数

3.1 抗三重线性速度拖引干扰仿真

针对三重线性速度拖引干扰进行抗干扰仿真,干扰参数见表3。

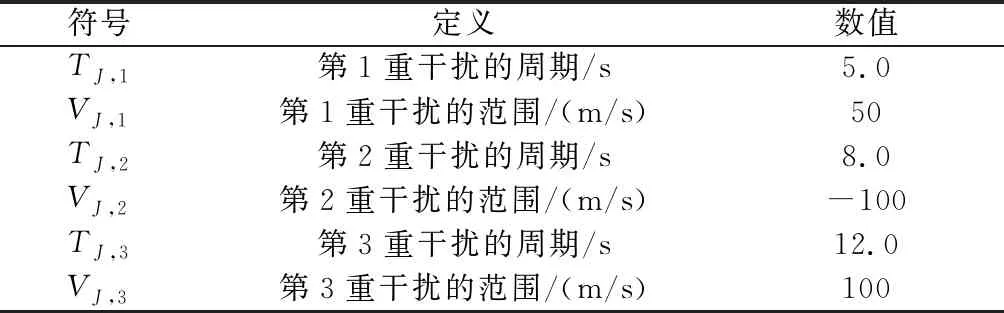
表3 三重线性速度拖引干扰参数

抗三重线性速度拖引干扰的仿真结果如图2～图6所示。

图2为雷达导引头径向速度量测曲线,图中量测1为真实目标径向接近速度,量测2～4为三重线性速度拖引干扰量测。

图3为目标速度向量估值,虚线为利用速度拖引干扰量测信息采用序贯SEKF算法估计得到的目标速度,蓝色实线为采用PDA滤波估计的目标速度。可以看出,虽然存在多重速度拖引干扰,采用PDA滤波仍然可以准确的估计出目标速度(图上PDA滤波结果与真值基本重合)。

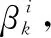
图5和图6分别为导弹加速度控制指令曲线和制导飞行中弹体姿态角曲线,蓝色实线为利用PDA滤波制导的结果,虚线为采用速度拖引干扰量测信息滤波制导的结果。可以看出,在存在多重速度拖引干扰时,采用PDA滤波导弹制导控制指令曲线和弹体姿态角曲线变化平稳,导弹脱靶量最小。

3.2 抗四重线性+非线性速度拖引干扰仿真

对四重线性+非线性速度拖引干扰进行抗干扰仿真,仿真结果如图7～图9所示。

图7为在四重速度拖引干扰环境中雷达导引头径向速度量测曲线,图中量测1为真实目标径向接近速度,量测2、3为线性速度拖引干扰,量测4、5为抛物线速度拖引干扰。

图8为PDA滤波计算过程中各量测与角度通道目标状态估值的关联概率。依然可以看出,速度拖引干扰偏离角度通道滤波给出的接近速度估值越远时其关联概率越低。通过关联概率可以抑制多重速度拖引干扰对目标状态信息估值的影响,如图9所示。

图9为目标速度向量估值,黑色实线为真值,红色虚线为采用PDA滤波估计的目标速度。可以看出,虽然存在四重线性+非线性速度拖引干扰,采用PDA滤波仍然可以准确的估计出目标速度。图中X向目标速度估值波动范围比Z向大的原因为:仿真态势中,目标X向速度与弹目视线偏角较小,易受速度拖引干扰的影响,但采用PDA滤波后X向目标速度估值误差仍能小于1 m/s。

在上述仿真条件下,分别进行了制导精度蒙特卡罗统计仿真(统计样本数1 000),脱靶量均值为0.26和0.39,进一步验证了PDA滤波抗多重速度拖引干扰的效果。

对于机动目标释放多重速度拖引干扰的情况,可以引入交互式多模型(interacting multiple models, IMM)算法,将IMM和PDA有机结合,构成交互式多模型PDA(IMMPDA)滤波算法[31],用于跟踪制导干扰、杂波环境中的单个机动目标。

4 结 论

多重速度拖引干扰会影响高重频PD雷达导引头对目标的跟踪和制导性能。针对此问题,本文在采用序贯SEKF算法处理雷达导引头角度测量信息和Doppler测量信息的基础上,提出了在序贯处理Doppler信息时采用PDA滤波抗多重速度拖引干扰的方法。PDA滤波计算每个Doppler量测信息与角度通道滤波给出的接近速度估值的关联概率,当Doppler测量信息偏离角度通道给出的接近速度估值越远时其关联概率越低,从而起到抑制速度拖引干扰的效果。仿真结果表明,该算法能对释放多重速度拖引干扰的目标进行稳定跟踪和制导。