基于改进LSTM模型的航空安全预测方法研究

曾 航, 张红梅, 任 博,2,*, 崔利杰, 武江南

(1. 空军工程大学装备管理与无人机工程学院, 陕西 西安, 710051; 2. 光电控制技术重点实验室, 河南 洛阳, 471000)

0 引 言

近年来，我国航空运输业发展迅猛，已成为我国交通运输的支柱产业，其在创造巨大经济效益的同时，也给守牢安全底线、预警重大险情加剧了压力。而精确的航空安全预测对开展事故预警意义重大,其能合理刻画航空安全状况的变化规律,为管理者作出事故预警决策提供科学依据。目前航空安全预测常用方法有时间序列预测、计量模型预测和机器学习预测等。

时间序列预测根据时间点划分样本集,通过分析各样本点间的相关性规律,预测其在未来时刻的变化趋势。常用的时间序列预测模型包括自回归滑动平均(auto-regressive moving average, ARMA)、差分自回归滑动平均(auto-regressive integrated moving average, ARIMA)模型等。该类方法基于历史样本信息价值,挖掘数字特征规律,对时序平稳的短期样本具有较好的解释性,但航空事故致因机理复杂,局部非平稳性显著,故预测精度偏低。计量模型预测基于统计学原理,将预测目标与影响因子的作用机理用数学方程组描述,观测主要因素的变化趋势,估计解析模型参数。常用方法有灰色预测、马尔可夫链预测和均生函数预测等。该类预测方法对先验知识积累量的依赖较强,即通过大量历史数据统计来估计样本分布特性,其在飞机发动机剩余寿命预测、装备平均故障间隔时间估计等领域应用成熟。但在航空安全预测领域,达到置信水平的解析模型尚未构建,预测结果的置信度较低。机器学习预测通过构建基于知识与规则的映射模型,设立目标约束函数优化模型参数,改进学习策略。文献[12]构建了基于贝叶斯推理机制的航空安全风险评估模型,能根据特征级精确预测对应的风险等级,但缺乏对风险水平的量化呈现,安全信息解释不充分。文献[13]将支持向量机(support vector machine, SVM)算法运用到飞行事故回归分析,结合径向基函数(radial basis function, RBF)核函数将样本非线性映射至高维空间,再作线性回归预测,结果证明SVM模型泛化能力较好。文献[14]提出了基于加权最小二乘SVM飞行事故率预测方法,采用最小二乘线性系统作为损失函数,加快学习速率的同时增强了鲁棒性。而随着样本特征维度的扩大,SVM训练量呈指数级增长,计算效率较低。文献[15]构建了多层感知机(multi-layer perceptron, MLP)预测模型,对Airclaims公司记载的230起非全损失事故进行回归分析和验证,仿真结果表明MLP算法在处理事故样本的高维特征、非线性映射关系上表现效果较好,但随着学习轮数的增加,易出现拟合和梯度更新异常问题。

随着人工智能、大数据等前沿技术的兴起,近年来深度学习成为机器学习的一个重要分支。其中,长短期记忆(long short-term memory, LSTM)神经网络正广泛应用于文本识别、用电负荷预测和风电功率预测等领域。文献[19]针对时间变量彼此独立,时序关系一般不被考虑的问题,采用LSTM神经网络模型预测鸟击事故征候数,结果证明LSTM模型对样本时序依赖特性的捕获能力较强,其精度优于传统模型。LSTM模型充分考虑了样本的时序相关性,对其非线性关系解释性较好。然而航空事故在特征维也呈现复杂的致因机理,单维的时序分析不能全面获取样本的数字特征。

综上,现有航空安全预测研究通过分析因果映射关系实现,但事故风险源与航空安全水平并非单一的因果映射关系,由于迟滞、回归等时序效应,安全水平还受到历史状态的影响。所以同一风险水平下的安全状况在不同时刻可能不相同。对此,本文提出基于堆叠式LSTM(multi layers LSTM, ML-LSTM)航空安全多步预测新方法:首先依据事故致因理论建立航空安全致因指标体系,通过pearson、sprearman和kendall关联指数分析剔除弱相关致因事件变量。其次,对输入输出样本集重新划分,以多时间窗口的致因事件状态和航空安全水平为输入集,未来若干时刻安全水平为输出集。最后构建ML-LSTM航空安全多步预测模型,对安全样本集进行训练及验证。

1 基于ML-LSTM多步预测建模

1.1 LSTM

LSTM网络结构如图1所示。

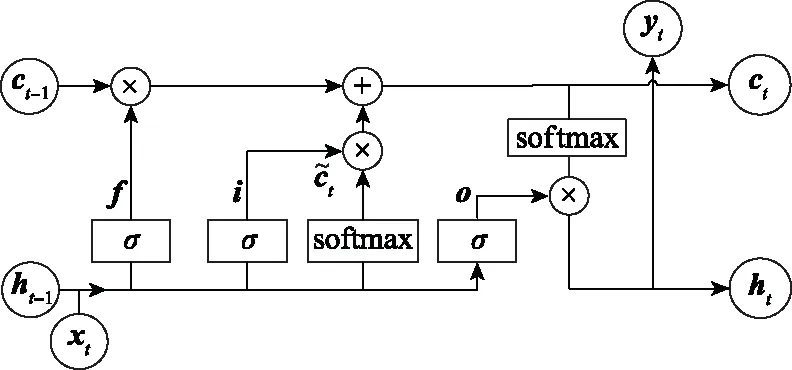
图1 LSTM网络结构Fig.1 LSTM network structure

门控单元：

(1)

(2)

(3)

存储单元:

(4)

(5)

输出状态:

=·tanh()

(6)

式中:、表示输入量和-1的权值;为偏置向量,用以调和门控激活函数的输入水平。(·)一般取sigmoid函数如下：

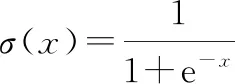
(7)

softmax激活函数取tanh(·)如下：

(8)

1.2 ML-LSTM网络多步预测模型

经典LSTM模型基于当前时刻样本点特征状态预测相应的输出指标,是点对点预测。但在实际的航空安全预测中,当前安全水平可能长期依赖于若干历史样本点状态,单样本迭代的训练模式难以高效捕获时序特性;从输出维考虑,点预测不能直观刻画未来一段时间内安全状态变化趋势。对此,本文尝试增大学习步长,提高模型并行处理样本效率。

同时,考虑到航空事故致因机理复杂。据最新研究公布,仅人的不安全行为因素就有28种,因此单层预测网络易出现欠拟合问题,对样本中隐含较深的时序信息挖掘能力不足。据此叠加LSTM网络的隐含层数,增强模型的非线性拟合能力同时加快学习速率,节约计算成本,对原网络结构进行改进,如图2所示。

图2 ML-LSTM时序多步航空安全预测模型Fig.2 Time series multi-step aviation safety prediction model based on ML-LSTM

图2中为单次训练输入的样本数,为预测步长，为隐含节点数,为隐含层数。前一隐含层的输出作为当前层的输入,第隐含层与预测端之间为全连接层(fully connected layer, FC),最后经softmax函数激活输出维预测向量。重构样本集的表达式如下。

隐含层输入端:

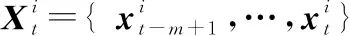
(9)

FC输入端:

={-+1,…,}

(10)

FC输出端:

={,…,+-1}

(11)

隐含层到FC层映射关系式:

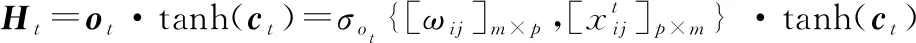
(12)

其中，

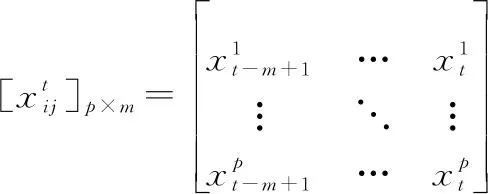
(13)

表示时刻下由个维时序样本重构的输入矩阵。

由式(1)、式(2)、式(4)和式(5)联合求解得出:

(14)

FC层到输出层映射关系式:

(15)

改进后的LSTM模型增大了输入样本维度,使其在单次训练中输入多组历史样本点,提高了现有样本的利用率;输出端增大预测步长,实现点预测向趋势预测的转化。与传统LSTM模型相比,实现对多组样本的并行处理,提升了记忆单元捕获时序规律的能力,更直观描述安全状况的动态走势,提升测算工作的实时性、前瞻性。此外,堆叠式隐含层结构扩展了模型的训练深度,增强模型的容错率和鲁棒性。

1.3 基于Adam算法超参数优化

在基于梯度下降的网络权值更新过程如下:

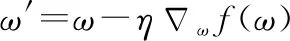
(16)

学习率的取值尤为关键,其直接决定了更新方向与模型收敛性能。传统网络一般采用固定学习率的方式,在后期易出现调幅过大而难以收敛的情况,影响模型的训练效果。

针对固定学习率的模型难收敛,而且手动调参工作繁琐的问题,本文采用基于自适应学习原理的Adam算法优化参数,该算法根据实时训练损失情况动态调整学习率,在误差容许的范围内加速模型收敛。优化流程如下。

首先计算梯度的一阶矩估计和二阶矩估计:

←-1+(1-)·

(17)

←-1+(1-)·

(18)

式中:、为一阶和二阶矩估计的衰减速率。

再计算修正矩估计的偏差项:

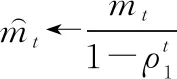
(19)

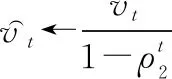
(20)

最后基于修正计算学习率更新值:

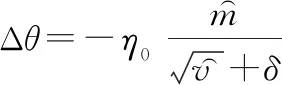
(21)

式中:为初始学习率。Adam通过矩估计的偏差修正,将学习率的更新值控制在可测范围,加快收敛速度的同时保证了模型鲁棒性。

1.4 基于ML-LSTM航空安全多步预测流程

预测流程如图3所示。

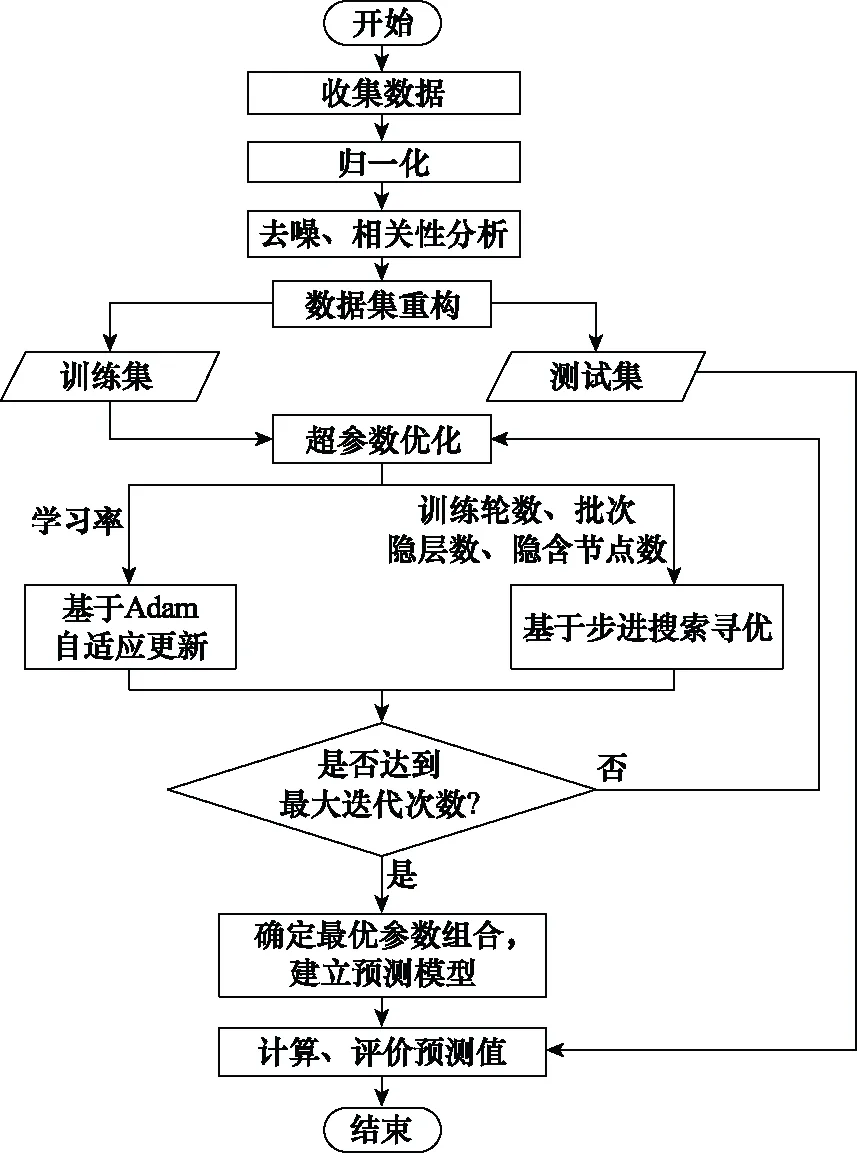
图3 基于ML-LSTM航空安全多步预测流程Fig.3 Multi-step prediction process of aviation safety based on ML-LSTM

(1) 数据预处理

为减少量纲差异对数据分析的干扰,采用min-max法对样本归一化:

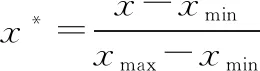
(22)

式中:、表示样本的最大值和最小值;、表示归一化前后的事故样本值。

经处理后的指标数值按固定比例缩放至区间[0,1]中。

(2) 相关性分析

各致因变量对航空安全的影响水平不尽相同,有必要定量计算各变量对航空安全水平的相关性,从而剔除弱相关变量,降低运算成本同时减少白噪声干扰。常用的相关系数有Pearson、Spearman和Kendall:

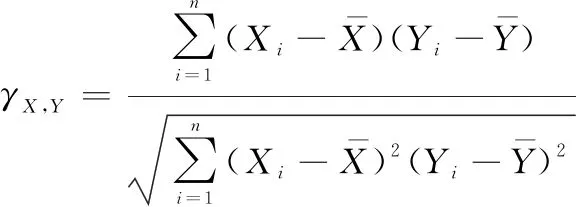
(23)

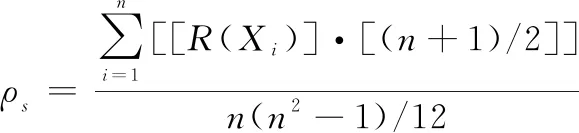
(24)

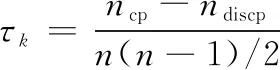
(25)

式中:表示观测点分别在两属性度量下排序一致的对数;表示排序不一致的对数。Pearson、Spearman和Kendall分别以定距、定序和定秩的尺度衡量因子相关性,能实现线性相关与单调相关的兼容分析。

(3) 航空安全预测模型构建

根据第12节构建ML-LSTM航空安全多步预测模型(见图3)。

(4) 超参数优化

用Adam算法优化学习率,以步进搜索形式遍历隐含层和节点数取值,比较不同参数组合下的均方根误差(root mean square error, RMSE):

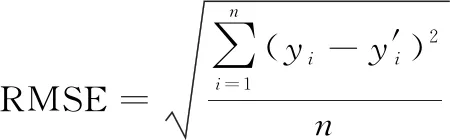
(26)

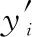
(5) 模型精度评价

为直观评价预测模型精度,以传统LSTM、循环神经网络(rerrent neural network, RNN)、门控循环单元(gated recurrent unit, GRU)、反向传播(back propagation, BP)、RBF神经网络和ARIMA预测方法作为对照模型,在相同实验环境计算预测结果。

2 算例验证

2.1 数据准备

2.1.1 数据收集

本文航空安全数据选自2019年度某型运输机事故统计,包括强制报告事件和不安全事件数据记录。其中强制报告事件数作为输出指标,强制报告事件是指造成了人员或财产等实际损失的事故,依规必须如实上报;不安全事件是诱发各类事故的风险源,虽未直接造成既定的损失,但与事故间存在着因果关联作用。经典SHEL事故致因理论认为,不安全事件的实质是以人为中心,与外界(软件、硬件和环境)及其内部间能量交互不当的结果。例如:由塔台指挥下达错误指令引发的不安全事件,实质为人员之间的信息交互不匹配。同时受限于人的认知水平,部分事件致因机理的可解释性较差(如机身卷入异物、不明碰撞物等),将此类事件归因为外来影响。据此不安全事件可划分为外来影响因素、设备设施因素、环境因素、管理因素和人为因素5类,作为候选输入指标,如图4所示。

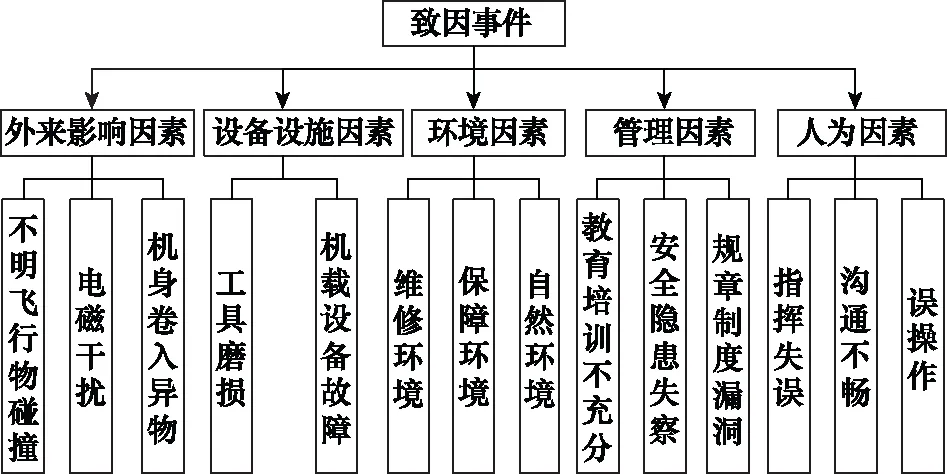
图4 致因事件数据指标体系Fig.4 Index system of cause data

2.1.2 样本集划分

为确保模型得到充分训练,同时具备可靠的泛化能力。将训练样本与测试样本的容量比设为5∶1,即前40周数据用于模型训练、参数优化,后8周数据用于验证模型预测精度。

2.2 数据预处理

由式(16)对各指标的周统计数据归一化处理,归一化结果如表1所示。

表1 某型运输机不安全事件周统计

经归一化的样本指标消除了单位和数量级的差异,并通过按比例缩放保留了原样本的数字特征规律。

2.3 相关性分析

利用可视化数据分析模块pandas_profile,定量计算各输入指标与强制报告事件数的相关指数(见式(23)～式(25)),并通过二维矩阵成像图显示运算结果如图5所示。事故为输出指标、外来影响、设备设施、环境、管理、人为分别表示5类不安全事件。矩阵单元的颜色表示指标之间的相关特性,其中蓝色表示正相关,红色表示负相关,颜色越深表示相关程度越强。

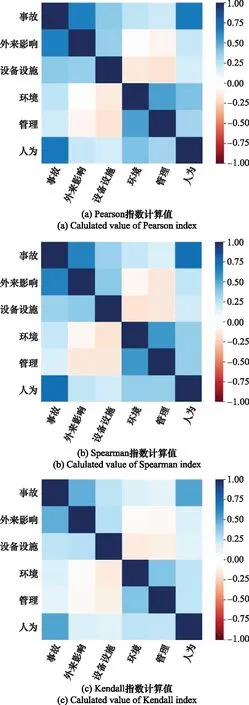
图5 相关性分析结果Fig.5 Correlation analysis results

各致因指标与事故关联度如表2所示。

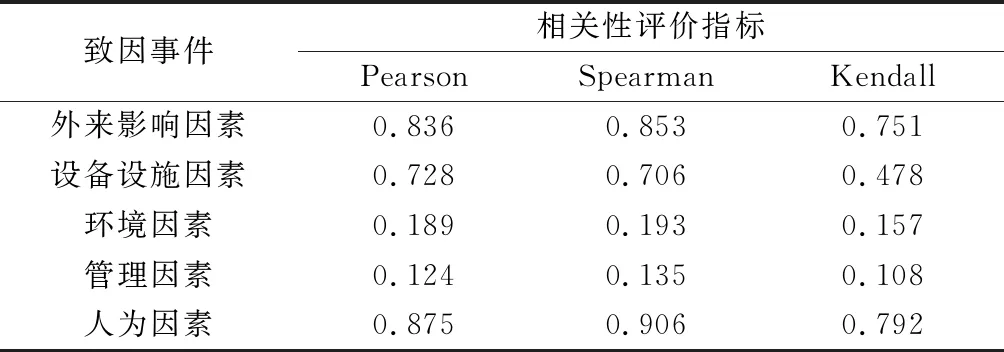
表2 致因指标与事故关联度

由相关性计算结果可知,在Pearson和Spearman指数上,外来影响因素、人为因素对事故的关联程度最大,均在0.85左右,设施设备因素次之,约为0.7;在Kendall指数上,外来影响因素、人为因素对事故的关联程度较大,超过了0.75。据此初步确立外来影响因素和人为因素作为强相关输入指标。

同时,环境因素与管理因素在3类评价指标呈现较弱的关联程度,均小于0.25。据此可剔除该两个变量作为输入指标。此外,考虑到设施设备因素在前两个评价尺度下的关联程度较强,说明其与事故的线性独立性、非线性单调相关性较显著,尽管Kendall指数略低,小于0.5,根据式(25)可逆推其呈现正相关的样本数比例高达85%,所以经综合分析可判定该指标与事故存在较强的正相关作用。最终选取外来影响因素、人为因素和设备设施因素作为输入指标。

2.4 模型参数优化

除学习率外,影响LSTM模型训练效果的关键参数还有隐含节点数(hidden_size)、隐含层数(layer_size)、训练轮数(epoch)、批尺寸(batch_size))和训练步长(time_step)。

隐含节点数和层数直接决定了模型的非线性拟合能力,在其数目足够多的环境下,理论上可逼近任意非线性分布特性的数据集,但同时可能引发过拟合问题;隐含节点数没有固定的计算方法,一般参照经验公式确定优选区间，如下：

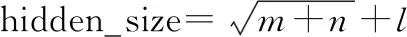
(27)

式中:为输入变量数;为输出变量数;为可调正常整数,取[1,10]。

训练轮数主要影响权值更新的效率,轮数过少会导致更新不充分,过多则增加了非必要运算成本;批尺寸是在一次学习中输入的样本集数,样本越多则迭代速度越快,但权值的调整幅度也将加大,给模型的收敛造成干扰。本文采取控制变量、步进搜索对比的方式优化上述参数。

训练步长是每个样本集所容纳的时序数据条数。对于输入集,步长过短难以捕获样本的长期依赖特性,过长会造成信息冗余、学习效率降低;对于输出集,步长过短无法直观描述安全状况变化趋势,过长会因输入信息不充分而加大预测误差。结合事故样本的实际容量,将输入、输出步长均设为4,即用近4周的历史信息预测未来4周的安全状况。

考虑到训练轮数未改变网络本身结构,属于外部环境变量,结合人为经验与样本容量,观测模型训练500轮下的损失变化情况。从图6可知,模型在前100轮训练过程中损失值降低幅度较大,在100～200轮过程中下降幅度逐渐放缓,模型趋于收敛。而在200轮之后训练损失稳定在01,增大训练轮数反而降低了测算效率,所以训练轮数阈值取200。

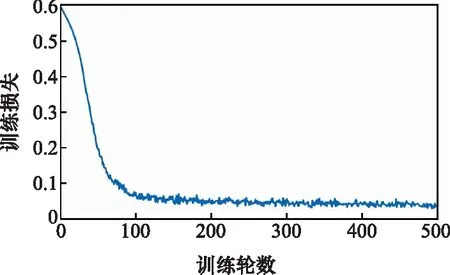
图6 训练损失随轮数变化趋势Fig.6 Changing trend of training loss with number of rounds

2.5 模型训练与精度评价

251 样本集重构

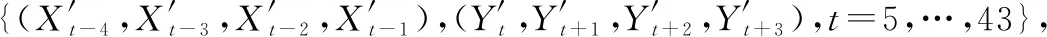
252 实验结果

依次调整参数隐含节点数和隐含层数,观测模型在不同批尺寸值下的预测效果。为缓解模型过拟合问题,每轮训练按5%的比例随机丢弃神经元(dropout_rate=005)。并考虑到网络的学习策略存在随机性,同一条件下的实验结果不尽相同。为提升模型稳健性,将同一模型重复实验10次,并求均值作为训练值。

首先调整参数隐含节点数,代入训练样本依次训练模型,将训练结果反归一化并计算RMSE，如表3所示,其中“*”标记为模型精度与鲁棒性最优对应的隐含节点数。

表3 不同隐含节点数下的预测精度对比

从表3中可看出,隐含节点数取11时模型精度有显著提升,并且随批尺寸的调整表现出较强的鲁棒性,据此确定单层网络隐含节点数最优解取11。

然后调整隐含层数,构建多层LSTM(multi-layer LSTM, ML-LSTM)航空安全多步预测模型,遍历各层隐含节点数组合下的训练误差,记录误差最小对应的参数组合,如表4所示,其中“**”标记为RMSE最小值。

表4 不同隐含层数下的预测精度对比

从表4中可看出:预测模型RMSE最小值为1.229 2,对应的输入参数layer_size=3,hidden_ size=(11,10,11),batch_size=2。为更直观评价本文模型预测效果,采取常规LSTM时序预测(见图1)、RNN、GRU、BP、RBF神经网络预测和ARIMA时序预测方法,在同一实验条件下用测试样本进行测算,预测效果对比如图7所示。从图7可以看出:① 本文所提出的模型(ML-LSTM)拟合效果最好,绝对数值与峰值走势均与测试样本(YTest)最为贴合,与经典LSTM模型相比,尽管后者数值逼近程度较高,但是对趋势的拟合欠佳,这说明ML-LSTM网络比经典LSTM更能捕获样本的趋势特性;② 循环类深度学习预测效果(RNN、LSTM、GRU)优于ARIMA,说明带有记忆元胞的深度学习模型与传统时序分析方法相比,对样本时序信息的提取、描述更加充分;③ BP和RBF两类神经网络预测模型均存在偏差过大的样本点,证明ML-LSTM网络鲁棒性优于传统机器学习模型。

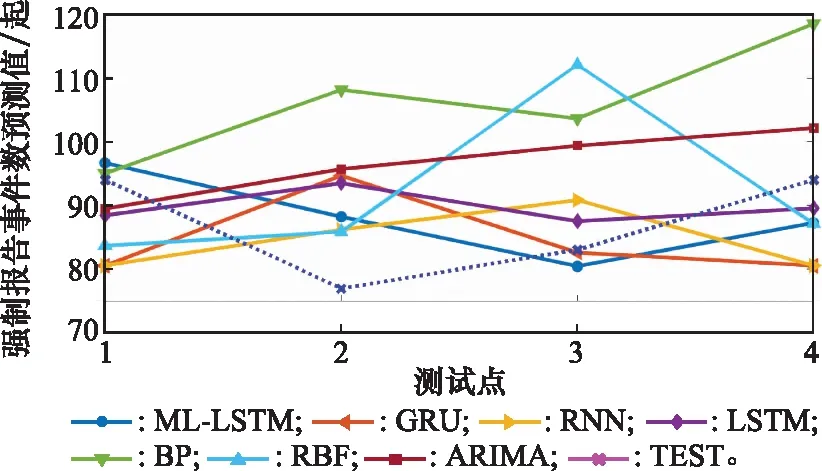
图7 预测模型结果对比Fig.7 Comparison of prediction effects

为便于定量评价模型泛化性能,记录各样本点绝对误差(absolute error, AE):

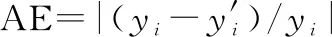
(28)

从表5可知,ML-LSTM精度上较传统LSTM有显著改进,前3个测试点误差分别降低了0.030 9、0.068 5、0.023 0,测试点4略有升高,但ML-LSTM模型总体鲁棒性明显增强。类似地,与GRU、RNN、RBF、BP模型相比,ML-LSTM预测模型均有3个测试点精度显著提升。与ARIMA模型相比,所有测试点在ML-LSTM预测模型均优于前者。证明ML-LSTM泛化能力有大幅提升。

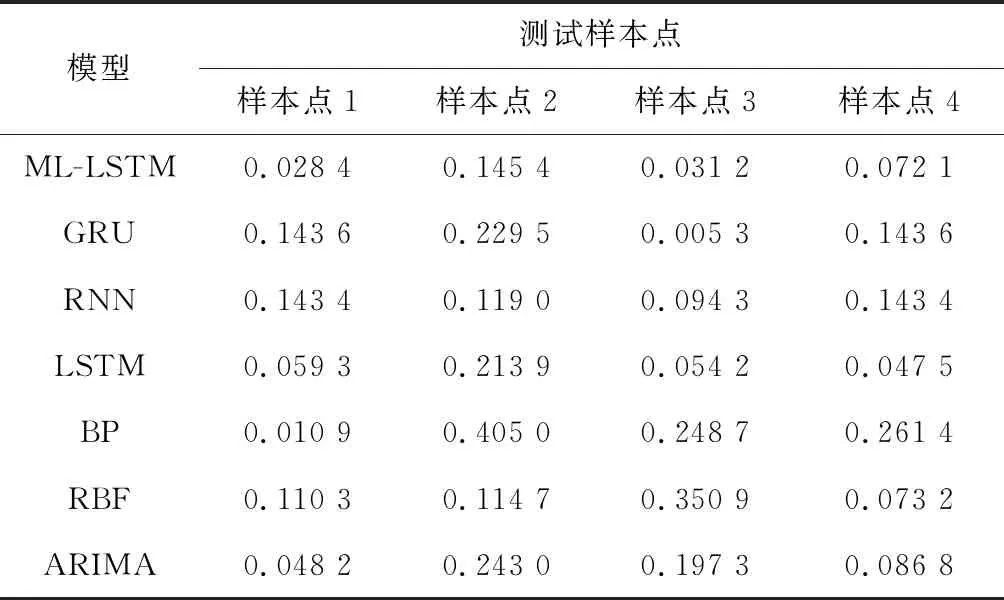
表5 各预测样本点AE值

循环上述过程,记录各模型10次实验结果RMSE分布情况从图8可知:① ML-LSTM预测误差最小,RMSE控制在6.5左右,较LSTM(9.5)误差降低了31.58%,证明本文所提方法准确性与鲁棒性较原模型有明显提升;② 循环类深度学习算法中,LSTM模型性能最好,RNN在前4次实验效果较佳,而后6次误差偏大,GRU模型误差分布平稳但数值偏大,证明对LSTM模型进行特定改进具备可行性与有效性;③ BP模型误差波动最大,大部分预测点RMSE在20以上;④ 由于RBF模型与ARIMA模型采用固定搜索的学习方式,RMSE值为常数(分别为16.44和13.28,远高于ML-LSTM)。

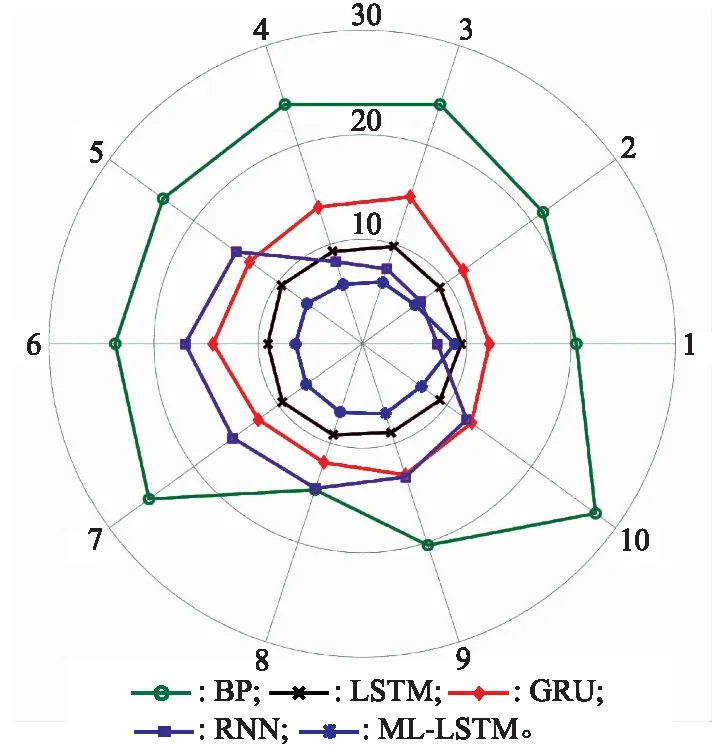
图8 10次实验RMSE分布图Fig.8 RMSE distribution diagram of ten experiments

3 结 论

本文针对LSTM训练模式为单步长迭代,难以高效处理致因机理复杂、迟滞效应显著的航空安全样本,提出了ML-LSTM多步预测模型。该模型从学习步长和隐含层深度两方面对经典LSTM结构做出改进,提升时序依赖捕获能力的同时,实现了点预测向趋势预测的转化。以2019年某型运输机事故样本为算例,实验结果表明ML-LSTM多步预测精度上显著优于传统预测方法,并具备良好的泛化能力和鲁棒性。