基于蜂群算法的坦克阵地部署与火力分配模型

褚凯轩, 常天庆, 孔德鹏, 张 雷, 孙皓泽

(1. 陆军装甲兵学院兵器与控制系, 北京 100072; 2. 中国人民解放军92942部队, 北京 100161; 3. 中国人民解放军78123部队, 四川 成都 610081)

0 引 言

多武器对多目标的协同火力打击能够有效地提高作战集群的整体作战效能,火力协同既能充分发挥多武器的作战优势,又能减少武器所受的战场威胁。坦克作为陆上主要突击武器,承担对敌一线防御阵地和纵深要点实施攻击的任务。仅打击决策这个层面,坦克分队对目标的射击问题是一个武器目标分配(weapon-target allocation, WTA)问题,与防空反导任务相似,但是坦克分队WTA模型与传统的防空反导类WTA模型有所不同。首先,坦克作为地面突击武器,具有高机动性,坦克不是定点的炮台而是移动的武器平台,因此坦克分队作战决策中,不仅需考虑谁打谁的问题,还需根据战场态势,决定坦克从集结区域到作战区域的兵力部署。其次,坦克作战是武器平台之间的攻防,而不是对导弹的拦截,因此需要考虑双方的动态对攻,既要考虑我方的打击策略也要考虑目标对我方的打击,只有将双方的博弈对抗特性加入到决策优化过程中,才能获得具有说服力的火力协同决策

WTA问题的实质是带约束的组合优化问题,是典型的非确定性多项式(non-deterministic polynomial, NP)问题。WTA问题的求解是目前的一个研究热点。如大规模邻域搜索算法、离散粒子群算法、蚁群算法、进化算法、人工蜂群(artificial bee colony, ABC)算法、遗传算法等,这些优化方法能够求得WTA问题的满意解。但是,战场态势瞬息万变,需在短时间内做出决策;而且NP类问题随着维数的增多解空间呈指数规模增长,当敌我数量较多时,优化算法耗时明显增长。考虑到战场态势变化迅速,尤其短兵相接时需要快速做出决策,因此继续研究提升群智能算法求解WTA模型的性能有重要意义。不同模型有其固有的特点,如果能够充分利用模型中的先验知识和特有规律,对群智能算法进行有针对的改进和具体设计,会取得良好的效果。

本文旨在优化坦克分队进攻战斗中,坦克从集结区域到作战区域的兵力部署决策和坦克在作战区域的火力分配决策。首先建立多对一的确定性火力对抗模型,在此基础上以目标价值加权平均毁伤概率最大为目标函数建立坦克火力分配模型;然后在坦克火力分配最优的基础上,建立坦克分队从集结区域到作战区域的数量分配模型,即坦克阵地部署模型。火力分配模型和阵地部署模型在逻辑上构成了双层迭代关系。算法方面,本文针对坦克火力分配模型和坦克阵地部署模型的实际情况,对ABC算法进行特定的应用和设计。最后,通过仿真实验对本文提出模型的有效性和算法的进步性进行验证。

1 模型介绍

坦克进攻战斗中,坦克分队在集结区域集结,之后分派到多个作战区域,参与对敌作战。如图1所示，为一次进攻战斗中坦克分队的作战决策图,包括阵地部署和火力分配,我方共计40辆坦克从集结区域出发,分派往10个射击区域,对15个目标进行打击,各射击区域坦克数量和各目标被分配的火力数量如图1中所示,其中火力分配阶段不同颜色的线段表示各目标分配的火力数量。通过合理的阵地部署和火力分配,可以实现决策优化,提高作战效能。

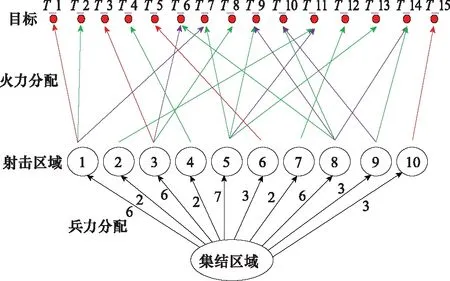
图1 作战决策图Fig.1 Operational decision graph

针对坦克分队作战中的阵地部署和火力分配的最优决策问题,本文建立双层迭代模型,如图2所示。阵地部署方案决定了坦克与目标的敌我毁伤概率,而敌我毁伤概率影响火力分配,是火力分配的依据,火力分配方案决定了作战效能。以最优作战效能为引导,搜索最优火力分配方案和最优阵地部署方案。模型的最终目标是找到最优的阵地部署方案以及与其配套的火力分配方案,两个模型同时最优,达到最佳的作战效能。

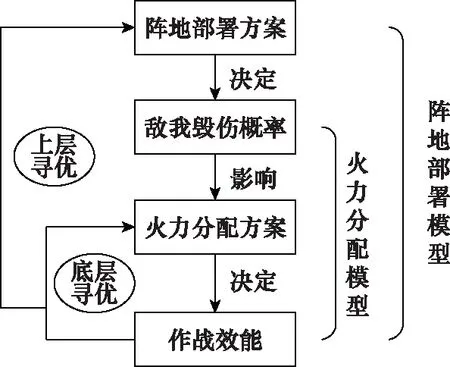
图2 双层迭代模型Fig.2 Two layer iterative model

辆坦克于集结区域集结完毕,待前往个射击区域,对个目标实施打击。模型表达式如下：

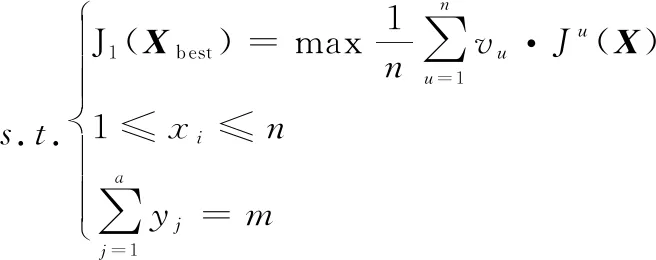
(1)

式中:(·)为底层寻优模型的评价函数;为目标个数;为目标的价值;()为当前火力分配方案下目标被毁伤的概率;向量为决策向量;=表示坦克打击目标;(·)为上层寻优模型的评价函数;()表示阵地部署方案下,采取最优火力分配方案时达到的作战效能;决策向量中,表示被分配到射击区域的坦克数量。模型表达式体现了双层迭代的思想,即阵地部署决策的优化必须以底层火力分配决策最优为基础。

现介绍确定型火力对抗下对目标毁伤概率的计算方法。不同于防空反导类WTA问题,坦克作战是一个动态的持续的对抗过程,我方坦克打击目标的同时,还要面临敌目标对我方坦克的攻击。由于地形等环境因素相对稳定,可假设在射击区域内,坦克对某一目标的毁伤概率和该目标对坦克的毁伤概率保持不变,我方各坦克最多发射次,各次发射相互独立。

我方指派辆坦克对目标实施打击,我方在第1次射击即毁伤目标的概率为

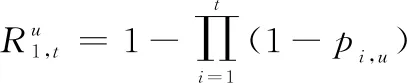
(2)

我方坦克第2次射击发生在敌目标第1轮打击后,第2轮射击坦克毁伤目标的概率为

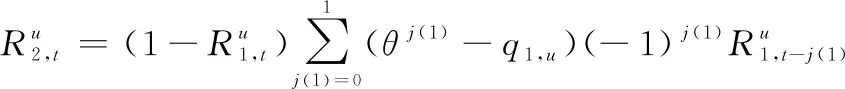
(3)

式中:为无穷小值,满足=1,=0。()为目标射击结果标记值,当()=1,表示目标第次射击毁伤我方一辆坦克,当()=0,表示目标第次射击未能毁伤我方坦克。

第3次射击毁伤目标的概率为

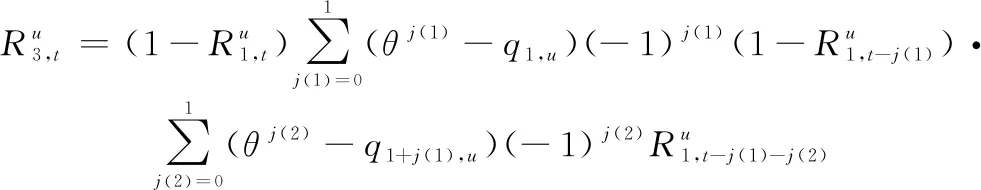
(4)

第次射击毁伤目标的概率为

(5)

综上所述,我方辆坦克能在次射击内,毁灭目标的概率为

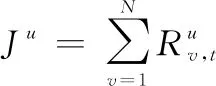
(6)

2 模型求解算法

模型M1是一种WTA模型,是一个典型的NP问题,随着坦克数量和目标数量的增多,解空间呈指数规律增长,模型M2虽然不是NP问题,但是随着坦克数量和可选射击区域的增多,解空间的数量也较大,且模型M2的求解需要以模型M1的结果为基础,是一种双层迭代,计算量巨大。本文针对模型M1和模型M2分别对ABC算法进行有针对性的设计和调整,以提高算法求解模型的收敛速度和收敛精度。

2.1 标准ABC算法

ABC算法是模拟蜜蜂采蜜行为的群智能算法,具有收敛良好、参数少、实现流程简单等优点。人工蜂群由雇佣蜂、观察蜂和侦查蜂组成。每个蜜蜂所在的位置即为一个可行解,所在位置对应蜜源的质量为解的质量。

211 初始化

对于一个维问题,每个蜜源的位置向量=[1,2,…,](=1,2,…,SN),SN表示种群个数。蜜源初始位置随机产生,解空间上限=[ub,ub,…,ub],下限=[lb,lb,…,lb],初始蜜源位置(即初始解)为

=lb+(ub-lb)·rand(0,1)

(7)

式中:=1,2,…,SN;=1,2,…,;为向量的第维变量;rand(0,1)是[0,1]上的随机数。

212 雇佣蜂

每一个蜜源对应一个雇佣蜂,蜜源处的雇佣蜂随机选择另一只蜜源处的蜜蜂进行邻域搜索并更新位置,获得新的蜜源：

=+(-)·rand(-1,1)

(8)

式中:为向量的第维变量;rand(-1,1)为[-1,1]上均匀分布的随机数;∈{1,2,…,SN},且满足≠。获得新的蜜源后,按照贪婪选择的方式更新蜜源。如果新的蜜源的质量高于原蜜源的质量,则取代;否则保持不变,迭代重复值trial加1,迭代重复值trial表示经过多次搜索,蜜源质量仍没有得到改善。

213 观察蜂

雇佣蜂更新一轮后,将蜜源信息分享给观察蜂,观察蜂根据蜜源的质量进行概率选择。第个蜜源被观察蜂选择的概率为

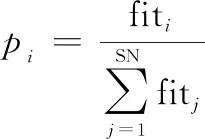
(9)

适应度值fit按照下式计算:

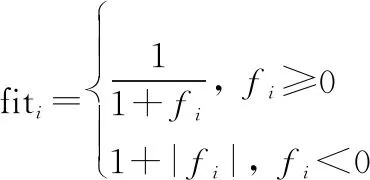
(10)

式中:是第个蜜源的评价值,由所求解问题的目标函数计算得。

观察蜂依据概率选择蜜源,与雇佣蜂相同,按照式(8)进行搜索。

214 侦查蜂

当雇佣蜂和观察蜂多次搜索未发生更新,即trial>limit时,则放弃该蜜源,变为侦查蜂,侦查蜂按照式(7)随机初始化一个新的蜜源代替。

2.2 坦克火力分配模型的ABC算法

坦克火力分配模型是一个典型的WTA模型,群智能算法是WTA模型求解的一个重要工具,学者对粒子群算法、协同拍卖算法、禁忌搜索算法、遗传算法、ABC算法等进行改进,用来解决WTA问题,显著提高了算法的收敛速度和收敛精度。本文针对提出的坦克火力分配模型特点,对ABC算法进行有针对性的设计。

2.2.1 初始化策略和侦察蜂策略

标准ABC算法种群初始化采取式(7)从整个解空间中随机选择,缺乏方向性,产生高质量解的概率较低。本文提出基于毁伤概率的种群初始化方法。初始化的解向量中,第个元素等于的概率为

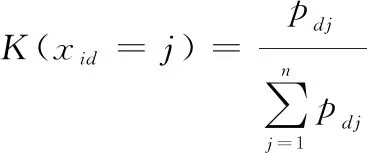
(11)

式中:为坦克对目标的命中概率。

采用式(11)进行初始化,使坦克更倾向于选择有较大命中概率的目标作为打击对象,更容易产生高质量的初始解。另外,当雇佣蜂或观察蜂放弃当前蜜源,变为侦查蜂时,也采取式(11)的方式产生新解。

222 搜索策略

标准ABC算法中,雇佣蜂和观察蜂都采用式(8)进行搜索,雇佣蜂是盲目搜索,没有任何方向性,只在进行贪婪选择时确保优质解被保留,观察蜂在选择邻居时,倾向于选择适应度高的个体作为邻居,有一定的方向性,但是针对WTA这类整数规划问题,收敛性不强。另外,在WTA的决策变量中,解向量中元素值代表的是目标的编号,不具有数字的意义。例如,当坦克打击目标9获得高打击收益,而坦克打击目标1获得低打击收益,采用式(8)进行优质解引导,可能会产生坦克对目标5进行打击,但是1、5、9仅仅是坦克的编号,这种引导没有实际意义。基于以上分析,本文对搜索策略进行如下改进。

(1) 雇佣蜂邻域最优解引导策略

雇佣蜂阶段应侧重探索能力,提高发现优良区域的概率。在雇佣蜂之间建立信息交互机制,每只雇佣蜂拥有各自的局部视野,能够发现局部视野内的最优解,并飞向局部最优解。通过这种方式,在雇佣蜂之间建立起了协作机制,雇佣蜂进化策略有了方向性。

定义雇佣蜂与距离公式：

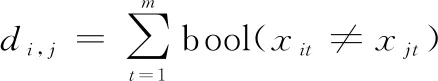
(12)

式中:bool为逻辑判断函数,当括号中内容为true时,bool值为1,当括号中内容为false时,bool值为0

定义雇佣蜂视野范围:

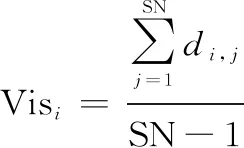
(13)

(2) 观察蜂全局精英引导策略

观察蜂拥有全局视野,能够发现全局的精英解,并飞向精英解所在位置。选择种群中适应度值最高的一部分群体组成精英群体,观察蜂随机选择精英解并接受引导。精英的数量

=ceil(·SN)

(14)

式中:为精英解比例;ceil(·)为向上取整函数。

(3) 替代策略

由于解向量中元素值不具备数字意义,固摒弃式(8)搜索方式,采取精英解(或邻域最优解)相应元素直接替代策略。

雇佣蜂搜索方程为

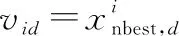
(15)

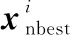
观察蜂搜索方程为

=gelite,

(16)

式中:表示随机选择的一个全局精英解。

223 选择策略

采用贪婪算法对雇佣蜂和观察蜂搜索之后的新旧解进行选择,该策略会造成过收敛,陷入局部最优,本文提出-贪心策略,更新过程中当新解适应度值高于旧解,以的概率选择新解,以1-的概率维持旧解。

-贪心策略公式为

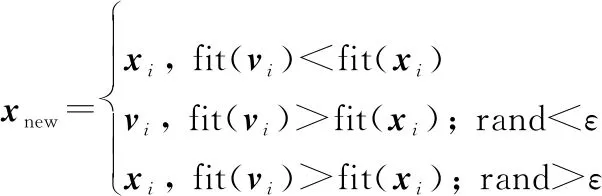
(17)

224 算法伪代码

坦克火力分配模型改进ABC算法伪代码如算法1所示。

算法 1 坦克火力分配模型改进ABC算法01初始化:根据式(11)产生SN个初始解x1,x2,…,xSN,根据式(10)计算初始解的适应度值fit(x1),fit(x2),…,fit(xSN)02while FESfit(xi)07 if r and<ε08 set xi=vi,triali=009 else10 xi,triali保持不变11 end if12 else13 xi保持不变,set triali=triali+114 end if15 set FES=FES+116 end for17 排序种群适应值,根据式(14)确定精英群体18 for i=1:SN19 随机选择精英解xgelite,根据式(16)产生新解vi20 if fit(vi)>fit(xi)21 if r and<ε22 set xi=vi,triali=023 else24 xi,triali保持不变25 end if26 else27 xi保持不变,set triali=triali+128 end if29 set FES=FES+130 end for31 for i=1:SN32 if traili>limit33 根据式(11)产生初始解,替换xi34 set triali=0,FES=FES+135 end if36 end for37 end while38 输出:全局最优解xbest,Jmax

2.3 坦克阵地部署模型的ABC算法

坦克阵地部署是确定从集结区域开进到各作战区域的坦克数量,为实现火力协同打下基础。坦克阵地部署也是一个整数规划模型,与火力分配模型不同的是,坦克阵地部署中,变量值具有数字的意义,表示该区域被分配的坦克数量,因此观察蜂的引导方程具备方向性。另外,模型M2中的约束条件在算法寻优中较苛刻,搜索过程中非常容易超出可行域,造成计算资源浪费。基于以上,本文提出针对坦克阵地部署的ABC算法。

2.3.1 雇佣蜂

采取式(12)和式(13)求取雇佣蜂的邻域最优解,采用下式进行更新:

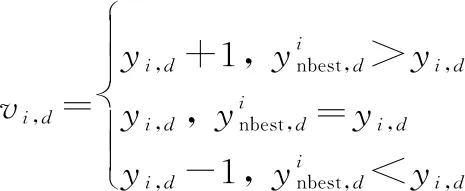
(18)

为避免新解超出可行域,直接引入修正算子

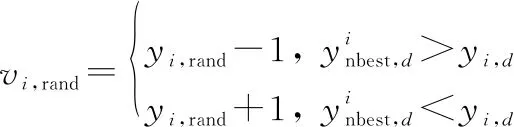
(19)

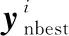
232 观察蜂

观察蜂随机选择全局精英解,并接受其引导:

(20)

修正算子：

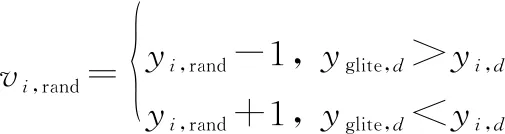
(21)

式中:为随机选择的一个精英解。

233 选择策略

采用-贪婪选择策略对雇佣蜂和观察蜂搜索之后的新旧解进行选择,同式(17)。

234 算法伪代码

坦克阵地部署改进算法伪代码如算法2所示。

算法 2 坦克阵地部署模型改进ABC算法01初始化:随机产生SN个初始解y1,y2,…,ySN,根据式(10)计算初始解的适应度值fit(y1),fit(y2),…,fit(ySN)02while FESfit(yi)07 if r and<ε08 set yi=vi,triali=009 else10 yi,triali保持不变11 end if12 else13 yi保持不变,set triali=triali+114 end if15 set FES=FES+116 end for17 排序种群适应值,根据式(14)确定精英群体18 for i=1:SN19 随机选择精英解ygelite,根据式(20)和式(21)产生新解vi20 if fit(vi)>fit(yi)21 if r and<ε22 set yi=vi,triali=023 else24 yi,triali保持不变25 end if26 else27 xi保持不变,set triali=triali+128 end if29 set FES=FES+130 end for31 for i=1:SN32 if triali>limit33 根据式(7)产生新解,替换yi34 set triali=0,FES=FES+135 end if36 end for37 end while38 输出:全局最优解ybest,Jmax

3 仿真实验

本节为了验证算法1和算法2的性能以及双层迭代优化策略的科学性,共设置3个实验。首先验证算法1用于求解坦克火力分配模型的性能,设置小、中、大3种规模战例进行实验验证,采取同样用于解决WTA问题的改进群智能算法作为对比,证明算法1的进步性。然后,验证算法2用于求解坦克阵地部署模型的性能,同样设置小、中、大3种规模战例进行比较实验,与经过benchmark检验的改进群智能算法比较,证明算法2中对ABC改进和设计的合理性。最后,用本文的双层迭代算法与文献[29]的层次风驱动优化(wind driven optimization, WDO)算法进行对比,证明本文双层迭代寻优策略的有效性。

3.1 实验1

共设定小规模、中规模、大规模3种战例,每种规模下,随机生成3组坦克阵地部署向量,各组测试的坦克数量、射击区域数量、目标数量及阵地部署方案设定如表1所示。坦克位于各射击区域时对目标毁伤概率如表2所示,目标对各射击区域内坦克的毁伤概率如表3所示。小规模战例共有10辆坦克,采用表中目标1～3、射击区域1～4的数据,中规模战例共有20辆坦克,采用表中目标1～7、射击区域1～7的数据,大规模战例共有40辆坦克,采用表中目标1～15、射击区域1～10的数据。为简便起见,所有战例均为我方坦克先发,最多射击3次,目标价值均为1。通过穷举的方式求得最优火力分配方案下的打击效益。最优打击效益和所需评价次数见表6。可以看出,采用穷举法所需的函数评价次数远远大于群智能算法的函数评价次数。

表1 战例设定

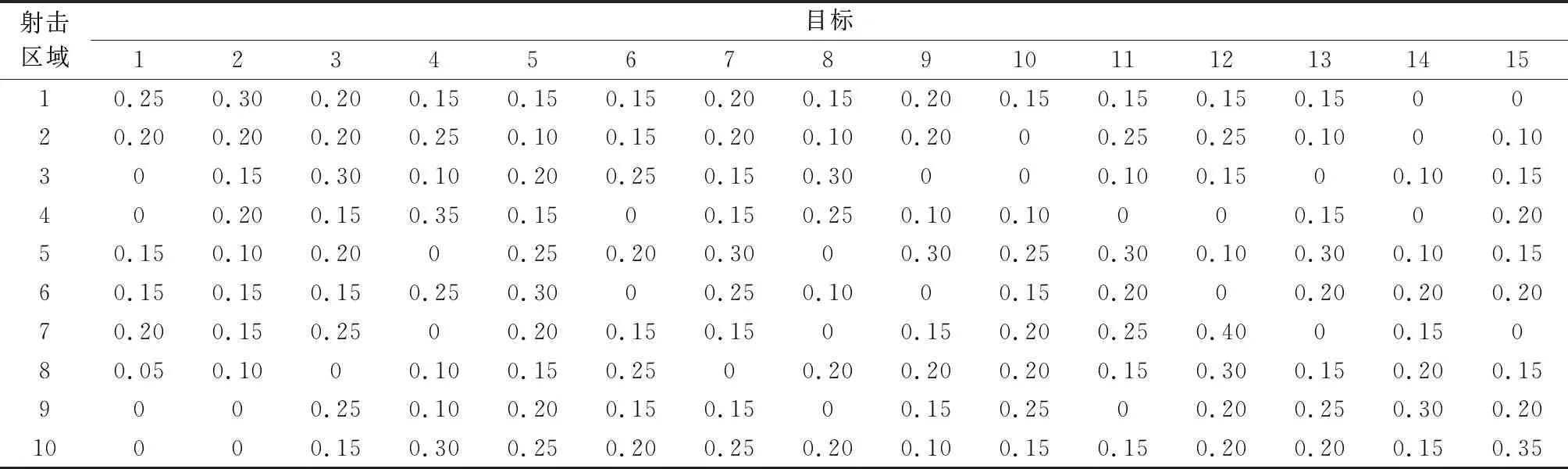
表2 射击区域对目标毁伤概率

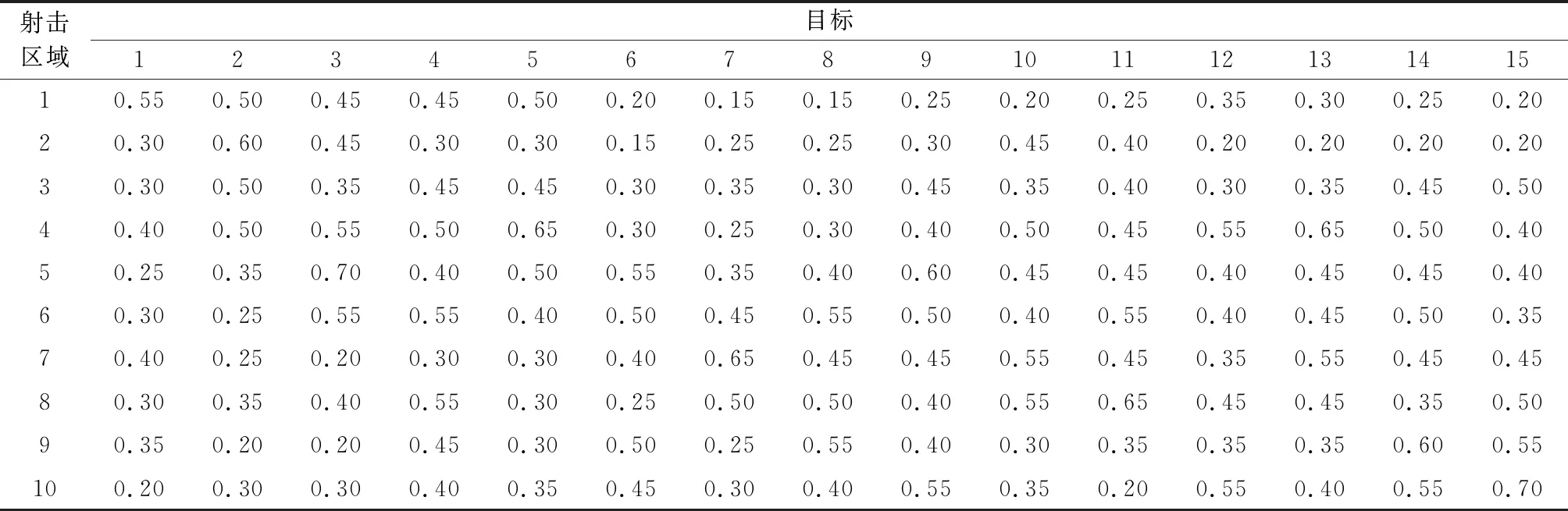
表3 目标对射击区域坦克毁伤概率

表4 最优打击效益和评价次数

为了验证算法1的性能,将算法1与ABC-NEH(Nawaz,Enscore,Ham)算法、随机邻域的自适应差分进化(random neighborhood adaptive differential evolution, RNADE)算法、IABC(ABC with heuristic factor initialization)算法和标准ABC算法进行对比实验,3种规模下算法的最大函数评价次数分别为2 000、16 000、40 000。每组实验各算法独立运行100遍。5种算法实验测试报告如表5所示。

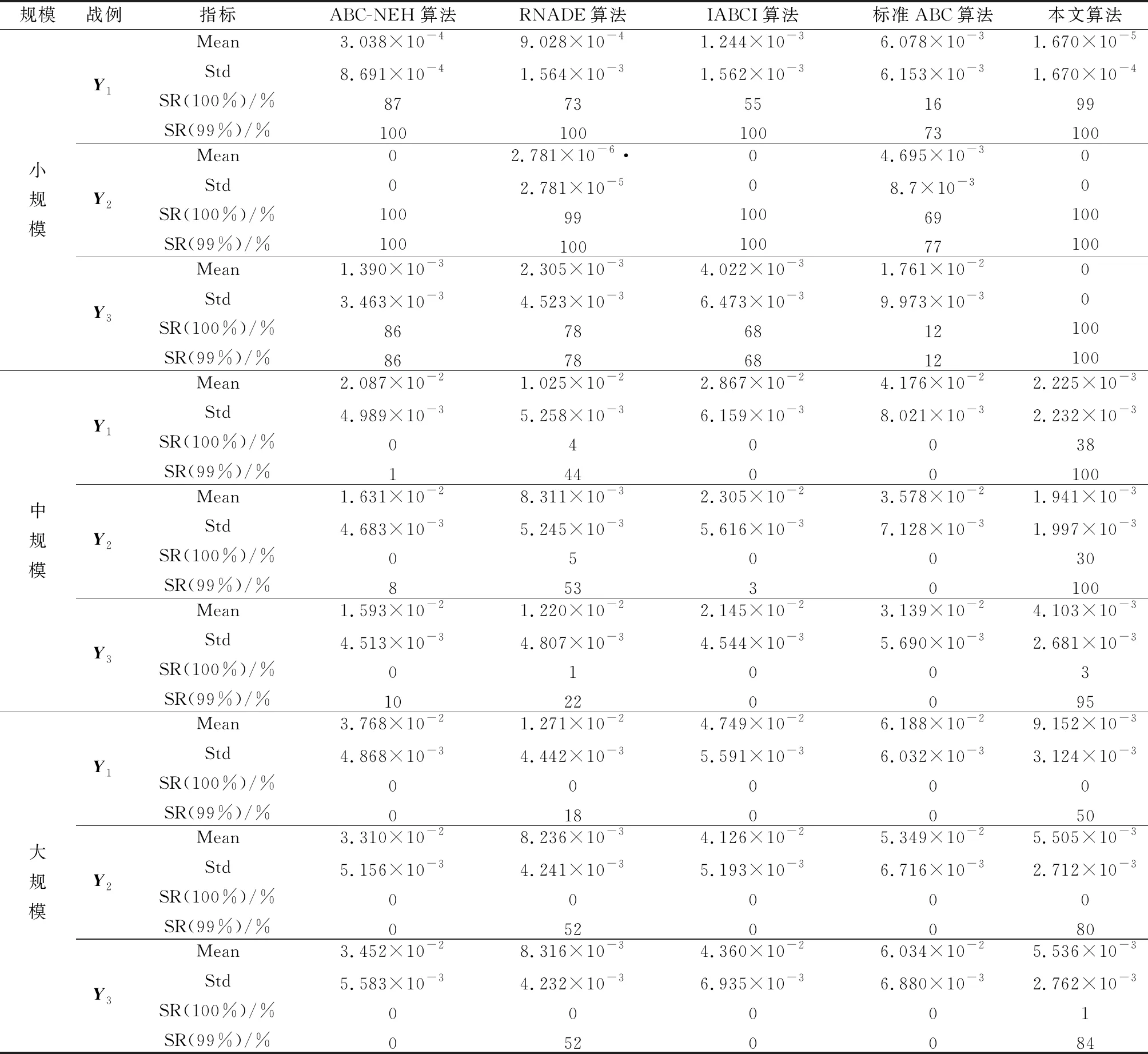
表5 5种算法求解M1实验测试报告

Mean表示算法求得的打击效益值与战例的理论最高效益值的差值的均值,Mean越接近0算法收敛性越好;Std表示各独立实验结果的标准差,Std越小算法稳定性越好。SR(100%)表示函数值在最大函数评价次数内收敛到最优值的概率,SR(99%)表示函数值在最大函数评价次数内收敛到0.99·的概率。从表5中数据可以看出,本文算法在小、中、大规模战例中均表现最好,小规模战例中,在规定评价次数内以100%的概率收敛到全局最优;中规模战例中以95%以上的概率收敛到0.99·;大规模战例中,以平均71%的概率收敛到0.99·。在算法的平均收敛精度(Mean)、收敛稳定性(Std)指标中,本文算法均优于对比算法。

为了更直观地展示各算法的收敛过程,3种规模战例、3种不同阵地部署方案下的火力分配模型的平均收敛曲线如图3～图5所示。可以看出,本文算法的收敛速度和收敛精度均优于其他算法。由于本文采取基于毁伤概率选择的种群初始化方法,初始解质量明显优于文献[20]、文献[21]和文献[23]的方法,文献[22]方法采用NEH的初始化方法,种群初始化水平也较高,但是该方法仅能在种群初始化阶段使用,且NEH方法产生的种群数量较少,而本文的初始化公式既可以在种群初始化时起作用,也能在侦察蜂阶段起到一定的方向性指引作用。文献[20]、文献[22]和文献[23]算法和本文的算法均优于标准ABC算法,说明对群智能算法的改进是有意义的。

图3 小规模战例火力分配模型平均收敛曲线Fig.3 Average convergence curve of small-scale battles firepower allocation

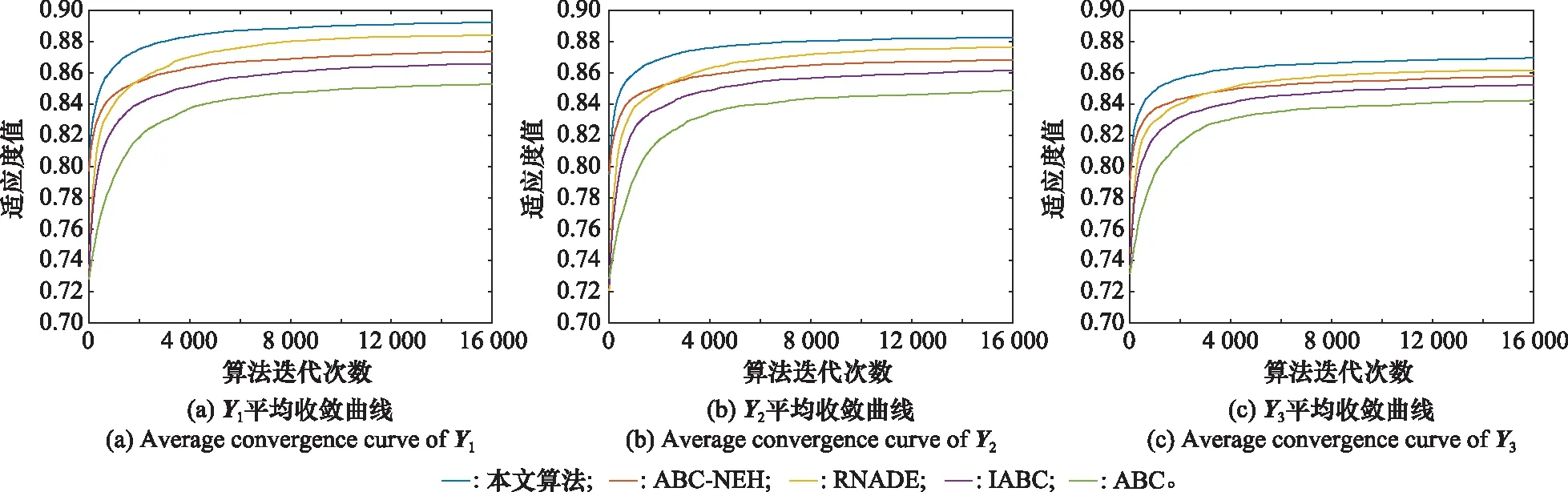
图4 中规模战例火力分配模型平均收敛曲线Fig.4 Average convergence curve of middle-scale battles firepower allocation

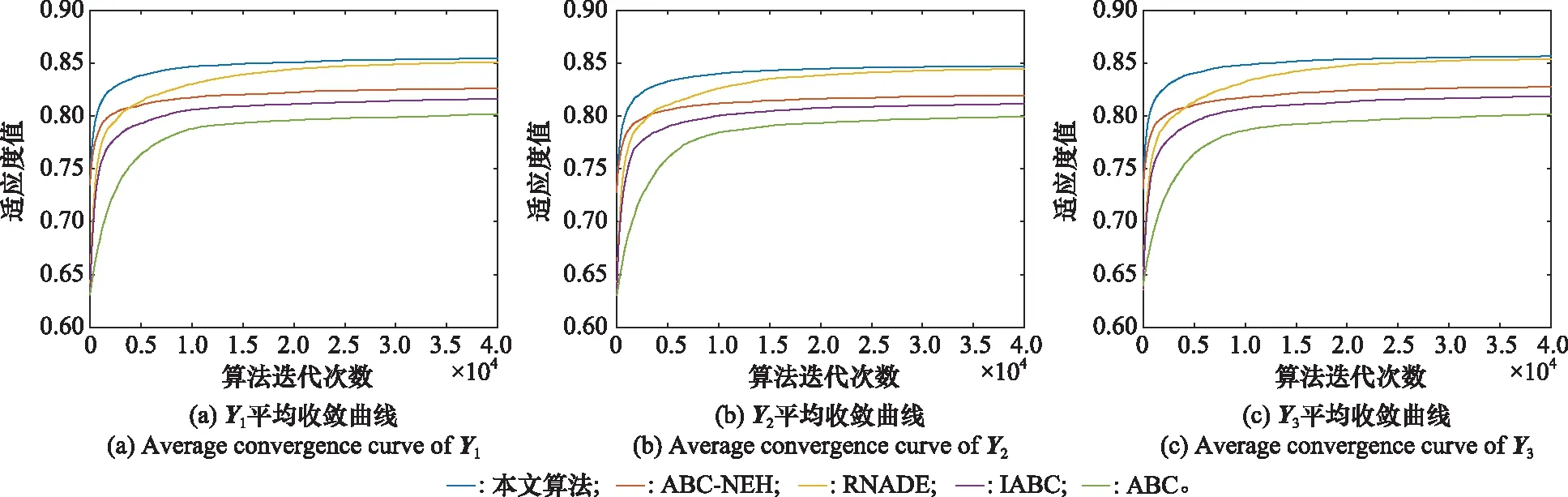
图5 大规模战例火力分配模型平均收敛曲线Fig.5 Average convergence curve of large-scale battles firepower allocation

3.2 实验2

在算法1的基础上,对算法2的性能进行验证。实验数据仍采用表2和表3中的坦克毁伤目标概率和目标毁伤坦克概率。坦克阵地部署模型是本文提出的原创模型,文献中没有针对该模型改进群智能算法,所以选择在benchmark上取得优良效果的算法作为对比算法,对比算法均采用罚函数应对约束条件。即

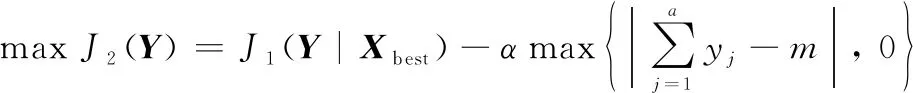
小、中、大3种规模战例中,最大函数适应度评价次数分别为500,2 000,8 000。4种指标Mean、Std、SR(100%)和SR(99%)的意义同实验1。通过穷举的方式,预先求得小规模战例和中规模战例的和,大规模战例由于解空间太大,无法通过穷举法获得最优解,以所有次实验获得的最优值近似看作大规模战例的,如表6所示。

表6 最优阵地部署方案及打击效益

为了验证算法2的性能,将算法2与qABC(quick ABC)、基于基因重组的人工蜂群 (ABC algorithm with gene recombination, GRABC)算法、eABC(ABC algorithm with elite guidance)和标准ABC算法进行对比实验。底层循环均采用本文的算法1。每组实验各算法独立运行25次。5种算法求解M2实验测试报告如表7所示。收敛曲线如图6所示。可以看出,除了大规模战例中eABC算法的标准差略小于本文算法,其他指标均为本文算法最优,本文算法的收敛速度和收敛精度优于其他算法。需要说明的是,实验2不能证明本文算法优于4种对比算法,因为本文算法是充分利用模型的先验知识和特定规律而有针对性的设计和调整,但是仅针对本文的阵地部署模型,本文算法在收敛速度和收敛精度上有明显优势,这种特定的设计是具有实用意义的。

大规模战例的最优阵地部署和火力分配决策如图1所示。40辆坦克从集结区域,向10个射击区域开进,各射击区域分配的坦克数量为6、2、6、2、7、3、2、6、3、3,坦克到达射击区域后对15个目标进行打击,可以看出,每个目标被分配的坦克数量均为2或3,考虑到共有40辆坦克、15个目标,这属于典型的分火射击,这是与实验中设定所有目标价值均为1有关,如果某目标战略地位较高,可设定高价值,模型和算法就会输出集火射击决策。

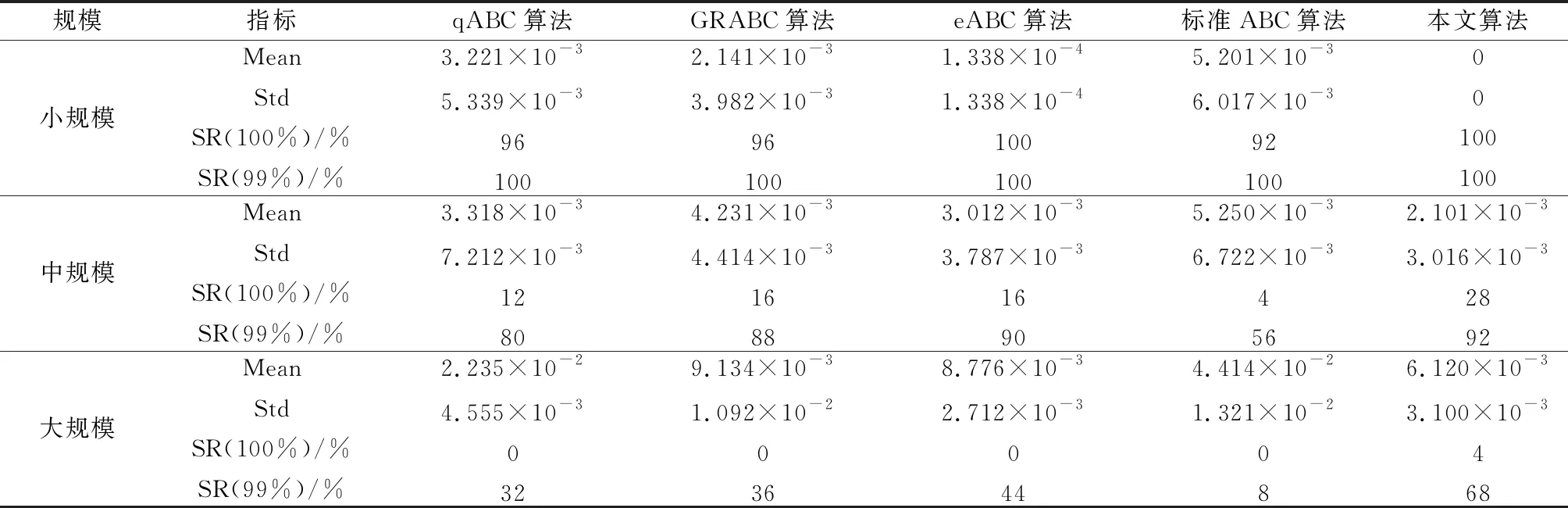
表7 5种算法求解M2实验测试报告

图6 阵地部署模型平均收敛曲线Fig.6 Average convergence curve of force allocation model

3.3 实验3

本实验将文献[29]的WDO算法作为对比算法,以证明本文算法双层迭代结构的合理性。层次WDO算法求解过程简述如下:

设定两层WDO算法的种群规模、迭代次数参数;

初始化上层、下层初始解、;

定住上层决策变量,在约束条件范围内,用WDO算法对下层模型优化求解,更新下层解;

定住下层决策变量,在约束条件范围内,用WDO算法对上层规划优化求解,更新上层解;

输出最优解、。

对比算法与本文算法采用相同的编码方式。由于对比算法采用的是“一定一动”交互迭代,无法独立分析各层的寻优能力,以最终寻优结果作为比较对象。本文算法和层次WDO求解双层迭代模型的结果对比如图7所示。

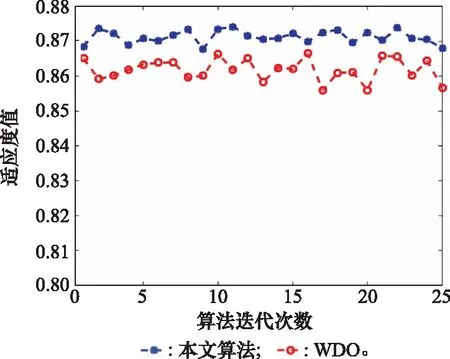
图7 本文算法和WDO算法求解模型结果对比Fig.7 Results comparison of solving the model by the proposed algorithm and WDO

从图7中可以看出,本文算法比WDO算法收敛精度更优,说明了本文提出的双层迭代寻优策略的有效性。WDO算法效果不理想的原因是该方法采用“一定一动”的交互迭代方式,对底层WTA问题没有充分寻优,而且火力分配和兵力问题是相互影响的,上层决策的变化会影响下层决策的科学性。本文双层迭代算法是在上层迭代计算中调用下层寻优计算的结果,可以有效地克服这一问题。上层迭代是以下层最优决策为基础,本质上是将上、下两层的迭代独立开,避免相互影响。实验一中的数据显示下层迭代在中、小规模战例中,以接近100%的概率收敛到0.99·、大规模战例中以平均71%的概率收敛到0.99,对下层迭代的充分开发以及下层优化算法的高收敛精度为上层迭代打下良好基础。

4 结 论

本文针对坦克分队进攻战斗中从集结区域到射击区域进军以及射击区域的火力打击中的决策问题,在考虑双方对抗关系的基础上,提出坦克火力分配模型和坦克阵地部署,为解决坦克分队兵力部署和火力协同提供了一种定量的决策方法。针对模型的特点对ABC算法进行有针对性的应用和设计,仿真实验表明采用的ABC算法在特定模型上收敛速度和收敛精度明显提高,在相同的适应度评估下,得到了更好的解决方案质量,可以显著提高作战中指挥决策的时效性和科学性。

下一步研究拟进一步充实阵地部署模型,结合实际战场情况,增加阵地部署模型的变量和影响行军的因素,比如进军途中的行进间射击和受到目标伏击情况,以及考虑行军队形对作战的影响。