面向动态交通流预测的双流图卷积网络

李朝阳，李 琳+，陶晓辉

1.武汉理工大学 计算机科学与技术学院，武汉430070

2.南昆士兰大学 理学院，澳大利亚 图文巴4350

交通预测为智能交通系统（intelligent transportation system，ITS）的决策提供了有力的依据，有助于缓解城市中的交通拥堵问题。近年来随着交通行业的发展，许多信息收集设备，如电磁线圈等，已经广泛部署在道路上。这些检测设备产生了多种形式的海量交通数据，包括交通流数据、浮动车数据、自行车数等。其中，交通流数据所包含的速度、交通量等参数通常被选作反映交通状况的基本测量指标，而交通流预测是交通管理部门进行交通管制的重要前提。

作为智能交通系统不可缺少的一部分，交通流预测一直是国内外研究重点。一般来说，交通流预测根据预测时长分为短期预测（≤30 min）和中长期预测（≥30 min）。相关研究中，早期大多采用传统的机器学习方法，如回归滑动平均模型（auto-regressive moving average model，ARIMA）及其他技术。这些方法将交通流看作一个简单的时间序列，因此对长期交通流的处理能力不足。近年来，随着深度学习技术在文本处理、语音识别等领域的发展，越来越多的研究也将深度学习应用于交通流预测领域。由于交通流数据是典型的时空数据，同时分析交通流的时间相关性和空间相关性是一个巨大的挑战。在分析时间相关性时，基于循环神经网络（recurrent neural network，RNN）、卷积神经网络（convolutional neural networks，CNN）的方法能充分捕捉当前时刻及历史时刻的时间信息。作为交通流预测的另一项重要工作，如何从已知的交通路网和交通流数据中充分挖掘空间相关性也受到了广泛关注。一些交通流预测模型将交通流数据视为图像和网格，然后应用卷积神经网络提取这些网格或图像内的空间特征。然而，基于卷积神经网络对属于图结构数据的交通流的空间相关性分析，仍然还在探索当中。

在交通流预测问题中，基于图卷积的方法可以直接在图结构数据上进行相关卷积操作。目前，基于GCN 的方法可以分为基于谱域的方法和基于空域的方法这两个主流方法。从基于谱域的角度来看，该方法通过对称的拉普拉斯矩阵来研究图的特性。因此，在处理有向图时，基于谱域的方法通常将有向图简化为无向图。而在现实世界中，交通流受下游交通流和上游交通流的影响不同，因此交通网络中检测节点之间的空间相关性表示为一组不对称的空间影响关系。如图1(3)所示，在时刻，节点v对节点v的影响强于v对v的影响。这说明空间相关性是有向的，且对其进行有效的分析和建模在交通流预测问题中至关重要。然而，基于谱域的GCN方法未充分考虑交通流数据有向的空间相关性。同样，一些基于空间的方法也未在交通流预测问题中充分考虑空间相关性的有向性。

此外，恶劣天气、交通事故等特殊的事件会影响驾驶者的交通行为，最终导致检测节点间的空间相关性发生改变。如图1 所示，时刻-1 到时刻，节点v对节点v在空间上的影响逐渐加强，同时其他节点之间的空间相关性也在不断变化。考虑到交通事故和恶劣天气可能会经常发生，动态空间相关性的有效建模对交通流预测的准确性至关重要。由于现实路网和驾驶者交通习惯的约束，从整体上看，交通流相关性也是稳定的。综上，本文认为交通流数据包括稳定分量和动态分量，且这两个部分的空间相关性具有不同的特性。然而，目前基于谱域图卷积的交通流预测研究通常认为节点间空间相关性仅基于其在现实路网中的连通关系，而且忽略了空间相关性的动态变化。

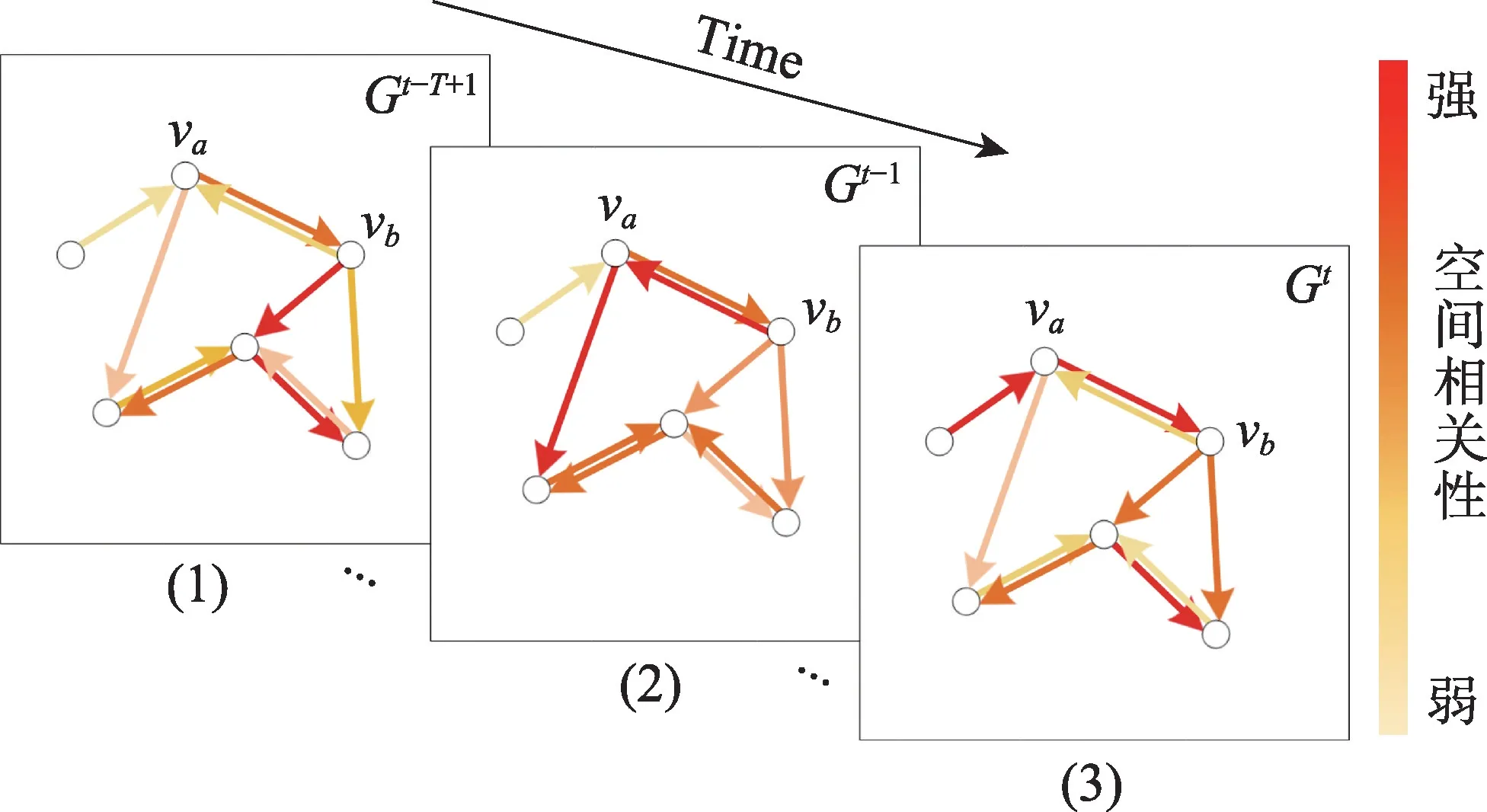
图1 交通流数据的时空相关性建模Fig.1 Spatial-temporal correlation modeling of traffic flow data

虽然有大量的交通流预测方法被提出，但如何同时考虑交通流数据空间相关性的动态性和有向性仍然是一个挑战。为了分析交通流数据复杂的动态时空相关性，本文提出了一种端到端的用于动态交通流预测的双流图卷积网络模型，设计了一组稳定和动态图卷积网络，因此本模型称为双流图卷积网络（two-stream graph convolution network，TSG-CN）。本文工作的主要贡献概括如下：

（1）构建双流图卷积层分别提取稳定空间相关性和动态空间相关性。首先，采用近似Tucker 分解的分解层将交通流数据划分为包含不同的空间相关性的稳定分量和动态分量。然后利用两个并行的基于空域的图卷积分别从稳定分量和动态分量中提取空间相关性，以提高动态交通流的预测能力。其中，采用基于空域的图卷积旨在捕捉非欧式空间数据的复杂拓扑结构。

（2）在两个真实的高速公路交通流数据集上进行了实验。结果证明，本文提出的TSGCN 模型的中长期和短期预测效果均优于其他几个现有的交通流预测方法。

1 相关工作

1.1 交通流预测

自20 世纪80 年代以来，交通预测问题经过不断研究和实践，取得了大量成果。交通预测问题包括预测所有交通相关的数据，如出租车需求和交通流（本文研究的问题）等。面向不同类型的交通数据的研究过程并不完全一致，因此本文只讨论交通流预测的问题。

已有很多学者在交通流预测问题上进行了大量尝试。早期的工作大都应用传统的机器学习方法来处理交通流数据，如ARIMA 等。然而，这类方法基于一些前提假设，因此对复杂非线性的交通流数据处理能力不足。随后发展起来的深度学习技术则能够对更复杂的数据进行建模。Sutskever 等人提出了一种通用的端到端序列学习方法，采用多层长短期记忆网络（long short-term memory，LSTM）提取复杂的时间相关性。Wu 等人采用基于卷积神经网络的空洞因果卷积，以更少的层数捕获较长的时间序列，因此可以更有效地学习时间相关性进行长期预测。此外，考虑到交通流数据本质上是时空数据，因此在空间维度上挖掘交通流数据的空间模式也是需要研究的重要问题。其中，基于卷积神经网络的方法大多通过将非欧式空间的交通流数据映射到欧式空间，如图像和网格，来提取空间相关性。由于传统卷积神经网络的平移不变性，只能处理标准的网格数据，该类方法并不适合应用于具有不同数量邻居的图结构数据。与之相比，图卷积可以直接在图结构数据上实现卷积操作，因此在处理交通流数据时具有优势。

1.2 基于图卷积的交通流预测

图卷积最早由Bruna 等人基于图谱的方法，采用将拉普拉斯矩阵的特征向量变换到谱域进行近似求解的方法提出，随后由Defferrard 等人利用傅里叶变换进行扩展优化。图卷积用于图结构数据的分析，如社交网络和文本分类。主流的图卷积方法包括基于谱域的方法和基于空域的方法。具体来说，基于谱域的方法借助图的拉普拉斯矩阵的特征值和特征向量来研究图的性质。Diao 等人提出了一种基于谱域的交通流预测方法，该方法基于图谱理论计算动态拉普拉斯矩阵。然而，由于基于谱域的方法在交通流预测问题中未充分考虑空间相关性的有向性，本文更倾向于使用基于空域的图卷积。

基于空域的方法对节点及其邻居进行卷积，其核心是选择合适的邻居。早期基于空间的方法未充分考虑交通流数据中的空间相关性的有向性。近期的方法却考虑到了这一点，使用双向随机游走来捕捉有向空间依赖性。Wu 等人进一步提出了从整个交通流数据中提取自适应邻接矩阵来表示隐含的有向空间相关性。然而，这些方法没有充分考虑检测节点间的空间相关性的动态变化。同时考虑到交通流预测问题中空间相关性的有向性和动态变化，本文提出了TSGCN 模型，将空间相关性细化为稳定空间相关性和动态空间相关性并分别考虑。

2 问题定义及相关知识

2.1 问题定义

如图1 所示，将空间路网定义有向图=(,,)，其中是节点集；为边集，表示节点间的连通性；∈R为中个节点的邻接矩阵,中非零元素代表两个连通节点的连接关系，如距离等。在时刻，表示为检测得到的交通流信号矩阵X∈R，其中是每个监测点检测的信号值（例如平均速度等），给定时段内历史数据X,X,…,X，本文研究的交通流预测问题是学习一个能够预测未来时段内交通流数据X, X,…,X的函数(·)，其映射关系表示为式（1）。

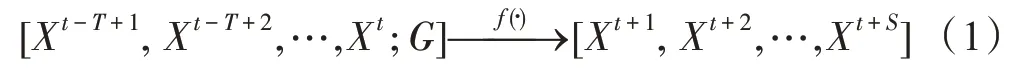
基于上述定义，需要同时对历史交通流数据的空间和时间相关性进行建模。图卷积可以从交通流数据中提取空间相关性，而扩散卷积则在图卷积的基础上进一步考虑交通流的有向性。

2.2 图卷积

图卷积分为基于谱域的图卷积和基于空域的图卷积两种方法。基于谱域的图卷积为了分析图的拓扑属性，将图用其对应的拉普拉斯矩阵表示为代数形式。因此在处理图结构时，首先需要用到拉普拉斯矩阵，一般定义为如式（2）所示。

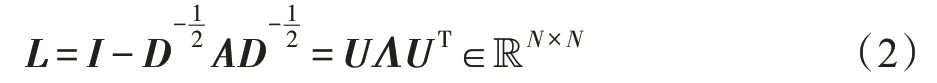
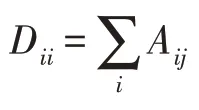
其中，*为图卷积操作；g为自学习运算符；∈R为输入数据。从基于谱域的角度看，有向图被简化为无向图并由其对应的拉普拉斯矩阵表示。考虑到交通图信号由交通网络中节点上交通流量的特征属性组成，其本质上是有向图结构。

基于空域的图卷积通过聚合和转换其邻居节点的信息来实现图结构数据上的卷积操作。为了捕获交通流数据受上游和下游的不同影响，扩散卷积使用前向和后向转移矩阵对有向交通图进行一组反向的随机游走。层扩散卷积过程定义如式（4）所示，更多详细信息在3.3 节中进行介绍。

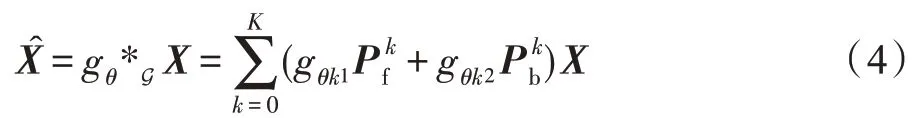
其中，=/()，=/()分别表示扩散卷积中的向前转移矩阵和向后转移矩阵。

3 TSGCN 模型

3.1 模型结构

本文提出的TSGCN 模型的总体框架如图2 上半部分所示，它主要由多层时空层组成。历史交通流数据经输入层转换后，传递到层叠加的时空层中。在每个时空层中，输入特征的残差被添加到时空块提取的输出特征中，作为下一层时空层的输入特征。最后，通过参数化的跳转连接，将各个时空层的输出特征连接送到输出层，最终得到预测结果。如图2 下半部分所示，时空层由时间模块和空间模块组成，分别用来对时间相关性和空间相关性进行建模。

图2 TSGCN 模型整体框架Fig.2 Framework of TSGCN model

时间相关性建模通过时间模块完成，如图2 左下角所示。具体来说，时间模块由两个并行的时间卷积和一个基于门控机制的激活单元（GTU）组成。基于上述方式构建的时间模块，可以利用输入数据的全时序来分析时序趋势，详细内容在3.2 节中介绍，更多细节来自文献[27]。时间相关性的建模不是本文的主要目标，可以选择其他先进的模型来替代它以提高性能。

本文主要的改进在于空间相关性建模，通过如图2 的右下角所示的空间模块完成。空间模块包含一个分解层和一个由S-GCN 和D-GCN 组成的双流图卷积层。首先，通过提取交通流数据的关键特征，分解层将输入的交通流数据分为稳定分量和动态分量。然后，通过双流图卷积层中的S-GCN 和D-GCN分别提取稳定和动态空间特征，经过拼接后作为整个时空层的输出。作为本文研究的重点，空间模块的具体内容将在3.3 节中介绍。

3.2 时间模块

时间模块如图2 的左下角所示，首先将输入特征∈R通过两个时间卷积捕获时间特征。采用基于CNN 的空洞因果卷积作为TSGCN 的时间卷积，以分析交通流数据中的时间相关性。空洞因果卷积通过指定步长来跳过相邻时刻交通流信息的方式，使本文提出的TSGCN 模型有能力对长期交通流数据进行处理。经过时间卷积后，时刻节点的交通流信息已包含其前面时刻的信息。然后将其作为GTU 中门控的输入，GTU 的计算形式如式（5）。

其中，*表示卷积运算；⊙表示元素Hadamard 乘积；(·)是sigmoid 激活函数，它控制当前状态传递到下一层的比率；W 和W分别是第层的滤波器和门控自学习卷积滤波器。

3.3 空间模块

TSGCN 模型的空间模块如图2 右下角所示，通过时间模块对交通流数据的时间特征进行建模后，将时间模块的输出特征与路网结构进行图卷积等操作。具体来说，本文采用基于空域图卷积方法进行图卷积操作，以捕捉交通流数据中有意义的空间相关性和特征。空间相关性对于提高交通流预测的准确性至关重要。为了获得准确的空间相关性，需要考虑以下两方面：（1）检测节点之间的空间相关性是有向的；（2）空间相关性在总体稳定的基础上不断波动。基于以上分析，本文构建的空间模块中首先引入了一个分解层，然后构建了一种用于动态空间相关性提取的双流图卷积神经网络。

Tucker分解是实现大规模数据处理的有效方法，可以从高阶张量分解出特征更加明显或结构更加简单的核心张量，从而更好地发掘数据内部的结构特征。本文采用近似Tucker 分解的分解层将输入数据划分为稳定和动态分量。Tucker 分解的核心思想是将一个阶的高维张量χ 分解为一个阶低维的核心张量G 和个因子矩阵,,…,U。首先，在输入数据时间和空间分别引入自学习时间投影因子∈R和空间投影因子∈R，从而获得输入数据∈R中的 时空核心张量G，如式（6）所示。

其中，和d分别为时空核心张量G 的时间维度和空间维度。时空核心张量G 包含了交通流数据的关键时空信息，然后通过式（7）将时空核心张量G 恢复至与输入数据相同维度，作为稳定分量∈R。

最后，将输入数据中减去稳定分量得到的剩余部分作为反映交通流动态变化的动态分量∈R。

通过上述分解层，可以从交通流数据中提取出稳定分量和动态分量。其中，稳定分量表示由固定的道路网络约束下的稳定性；动态分量代表了由于受到交通环境短期改变导致的动态变化。

考虑到稳定和动态分量包含不同的交通流数据，且具有不同的空间相关性，本文构建双流图卷积层从稳定分量∈R和动态分量∈R中分别分析空间相关性，如图3 所示。

稳定分量的空间相关性分析过程如图3 上部所示。交通流数据中的稳定分量表示受固定路网约束的部分，同时考虑到邻接矩阵可以表示路网结构。本文基于有向扩散卷积构建S-GCN 从稳定分量中提取有向的稳定空间相关性，计算过程如式（4）所示。

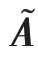
图3 双流图卷积层结构图Fig.3 Process of two-stream GCN layer

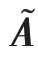
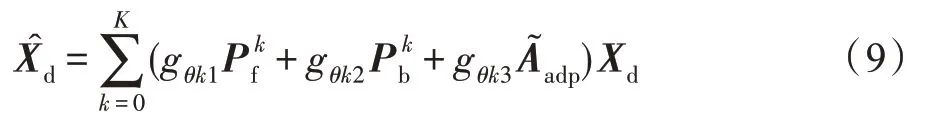
3.4 损失函数

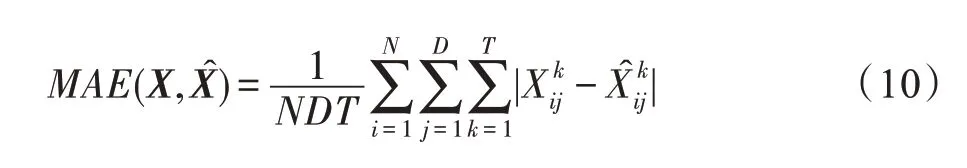
4 实验与结果

4.1 数据集和度量标准

为了评估本文提出的TSGCN 模型的性能，使用美国洛杉矶和加利福尼亚州的两个真实高速公路交通流数据集进行了实验。

（1）METR-LA：包含来自洛杉矶高速公路段上部署的环路检测器的交通信息。METR-LA 数据集选择了由1 515 条道路连接的207 个传感器，并在2012年3 月1 日 至2012年6月30日的4个月内每2 min 记录一次交通速度，包含的观测值总数为34 272。

（2）PeMS-BAY：包含PeMS（Caltrans performance measurement system）在加州湾区高速公路上收集的真实速度数据。PeMS-BAY 数据集选择了由2 369 条道路连接的325 个传感器，从2017 年1 月1 日到2017年5 月31 日，以每30 s 的间隔收集6 个月的数据。包含的观测值总数为52 116 个。

本文基于文献[16]发布的METR-LA 和PeMSBAY 数据集进行实验。由于公开的数据集已经过筛选等预处理操作，没有缺失值，其值分布如图4 所示。数据集还包含一个预定义的邻接矩阵，该矩阵根据传感器间的距离来反映连接关系。

图4 METR-LA 数据集和PEMS-BAY数据集测试数据可视化Fig.4 Visualization of test data of METR-LA and PEMS-BAY datasets

本文采用与对比方法相同的数据预处理方式，将数据汇总成以5 min 为时间间隔的样本，且通过ZScore 方法进行归一化。根据时间顺序对数据集进行划分，其中70%用于训练，10%用于验证，20%用于测试。所有实验都根据过去60 min 内12 个观测时刻的历史交通流数据来预测交通流的平均速度。为了评估TSGCN 模型的性能，本文使用3 个误差评估指标，包括平均绝对误差、均方根误差（root mean square error，）和平均绝对百分比误差（mean absolute percentage error，）。其中，计算如式（10）所示，计算如式（11）所示，计算如式（12）所示。

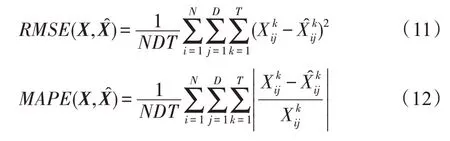
4.2 对比方法和实验设置

将本文提出的模型与以下四种交通流预测方法进行比较：

（1）ARIMA：带有卡尔曼滤波器的自回归积分滑动平均法，是一种经典的时间序列分析模型。

（2）FC-LSTM：具有全连接层的长短时记忆网络，是一种经典的递归神经网络。

（3）DCRNN：扩散卷积神经网络在时间维度上使用编码器-解码器结构，在空间维度上使用双向随机游走，是一种基于空域的GCN 方法。

（4）Graph WaveNet：一种用于时空图建模的卷积网络体系结构，在交通流预测问题上取得了很好的效果。

4.3 实验设置

本文基于Pytorch 框架实现了包含8 个堆叠的时空层的TSGCN 模型。其中，时间模块中时间卷积的扩散参数分别为1、2、1、2、1、2、1、2，且时间卷积核的长度在每一层中为2，输出通道为32。

空间模块包含一个分解层和一个双流图卷积层。TSGCN 模型通过分解层将交通流数据划分为稳定分量和动态分量，因此分解层是模型的一个重要组成部分。为了选择核心张量G 在空间上最优的空间维度，本文选择了不同的维度分别进行实验，并基于3 个误差指标进行对比。

由于METR-LA 数据集包含207 个监测点，从[32，64，100，128]中进行核心空间维度的选择。根据如图5 所示的误差值，本文将核心张量的空间维度设为100。同时，在PeMS-BAY 数据集的实验中设为160。作为空间模块另一个重要组成部分，双流图卷积层中的输出通道仍设置为32，其中图卷积层的卷积核均设为1。

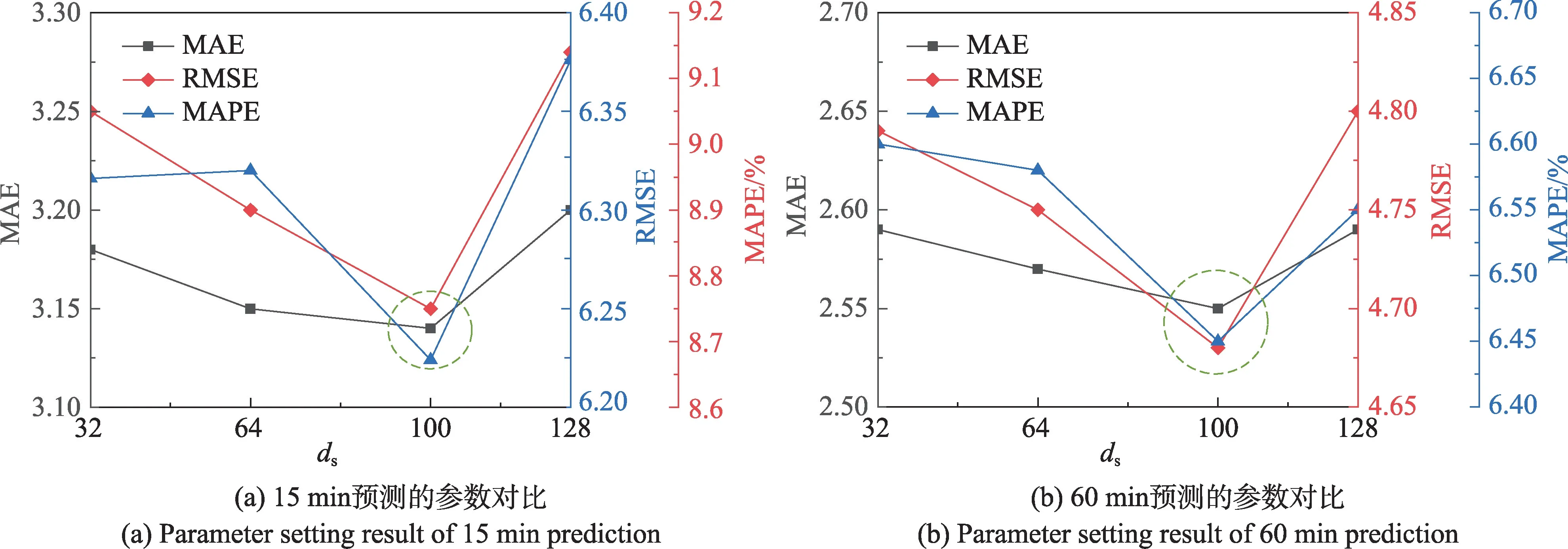
图5 基于METR-LA 数据集的参数ds 设置对比Fig.5 Comparison of parameter ds setting based on METR-LA dataset

TSGCN 模型的训练优化器采用Adam 算法，初始学习率为0.001，在70 个周期后的衰减率为0.1。实验在Intel Xeon CPU和NVIDIA Titan XP显卡上进行。

4.4 实验结果分析

本文在两个真实数据集上将提出的TSGCN 模型与4 个对比方法进行了比较。由于使用了相同的数据集和相同的预测范围，本文引用了文献[17]公开的ARIMA、FC-LSTM、DCRNN 结果，及文献[18]公开的Graph WaveNet 的结果。表1 显示了TSGCN 和对比方法在预测未来15 min、30 min 和60 min 交通流的实验结果。可以看出，本文提出的TSGCN 模型在两个数据集上均表现最佳。并且与对比方法相比，3 个评价指标以相似的幅度减小。例如，与Graph WaveNet相比，在对未来60 min 的流量预测中，在METR-LA数据集上的MAE 和RMSE 分别降低了约11.1%、15.3%；在PeMS-BAY 数据集上的MAE 和RMSE 则分别降低了16.9%、20.1%。

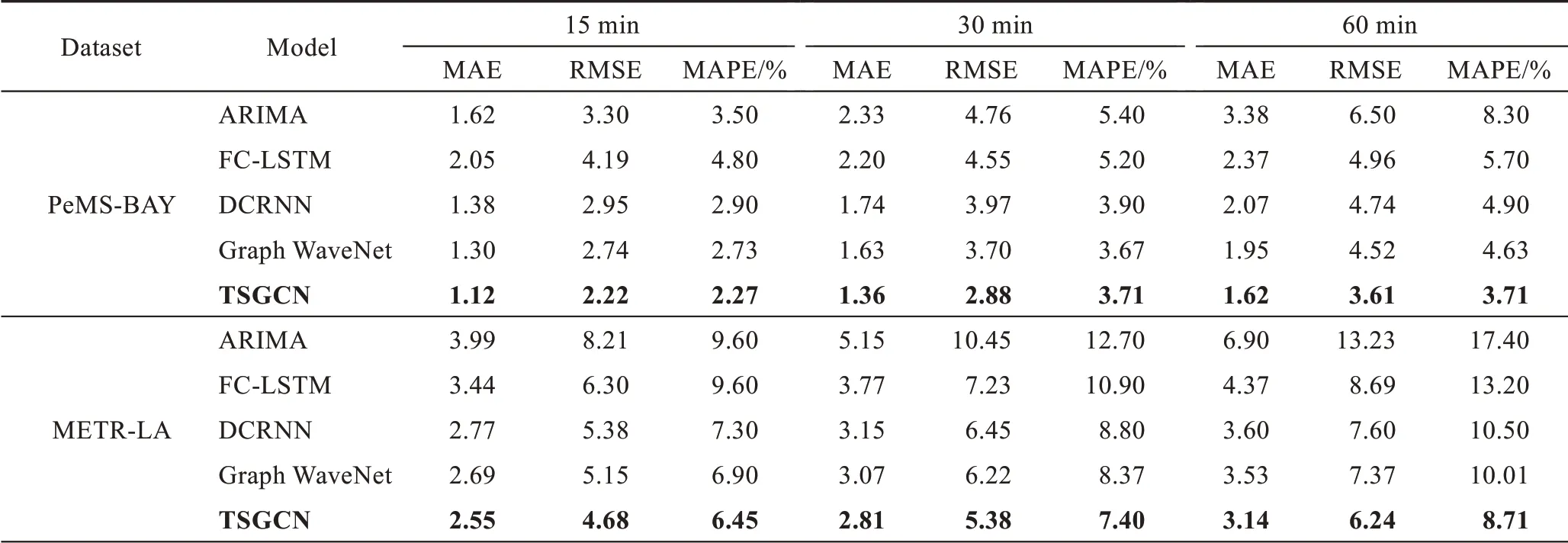
表1 TSGCN 模型与基线模型的性能对比Table 1 Performance comparison of TSGCN with baseline models

相比之下，传统的时间序列分析方法ARIMA 由于无法处理复杂的交通流数据而预测误差最大。此外，同时考虑时间和空间相关性的模型（包括DCRNN、Graph WaveNet和TSGCN）优于仅考虑时间因素的深度学习模型FC-LSTM。值得注意的是，与其他时空模型相比，本文提出的TSGCN 在短期和长期预测任务中都超过了DCRNN 和Graph WaveNet这两个基于空域图卷积的交通流预测模型，这表明考虑动态空间相关性对交通流预测具有不可忽视的作用。

4.5 模型分析

为了更好地分析TSGCN 模型，本文随机选择了一个监测点并对其在测试集上一周内的预测值进行了可视化操作，如图6 所示。TSGCN 模型能检测到出现较大波动的开始和结束时刻，并能够较好地拟合交通流的速度。由图6 可知，在短期预测和长期预测中，较大的误差出现在谷值点。这是由于TSGCN模型将交通流数据划分为稳定和波动分量并分别进行空间相关性建模，而最终的预测结果受稳定和波动两种空间相关性的同时影响。稳定部分受路网和交通习惯的约束部分，在图6 中表示为除25 日和26日两天外其他日期的近似时刻均有一个速度大幅下降的波动。在误差较大的谷值点，TSGCN 的预测值低于真实值，即呈现出类似于过去谷值的特点，体现出稳定空间相关性的影响。此外，TSGCN 模型的预测值与真实值之间存在一定误差，如何更准确地拟合波动谷值处的交通流速度也是下一步要考虑的重点。

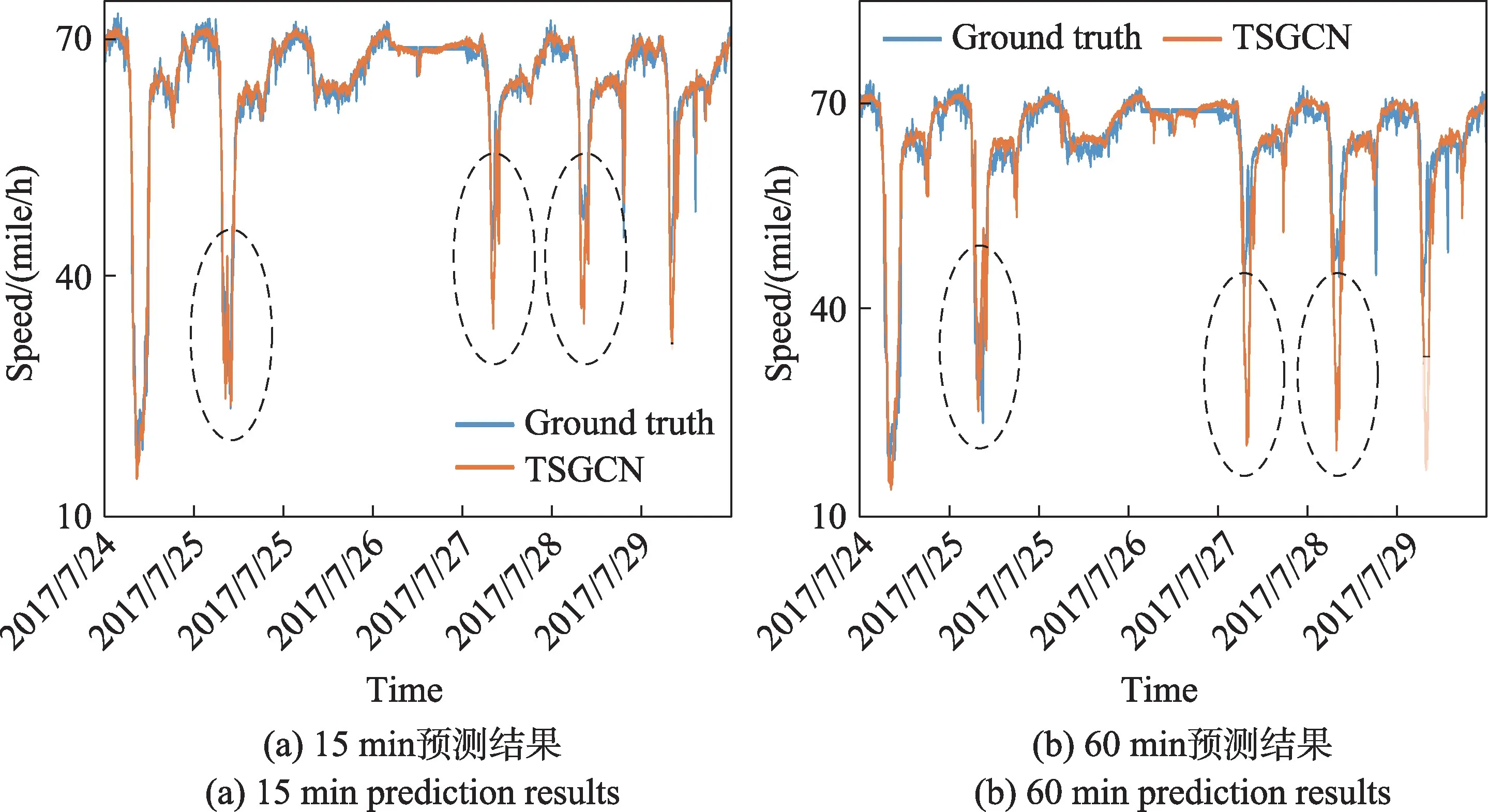
图6 METR-LA 数据集一周内数据可视化结果Fig.6 Visualization results within one week on METR-LA dataset

TSGCN 模型通过分解层将交通流数据划分出动态分量，进一步从动态分量中提取动态空间相关性用于预测。动态空间相关性在更有效的交通流预测问题中起着至关重要的作用。本文提出的TSGCN模型在短期预测和中长期预测问题上都优于其他对比方法。并且随着预测时间的延长，预测性能提升越大，如图7 所示。例如，在METR-LA 数据集上，与目前较新的交通流预测方法Graph WaveNet 相比，对未来15 min 的预测时，本文提出的TSGCN 模型的MAE 误差值降低了5.20%；对于60 min 的预测则降低了约11.1%。可以认为TSGCN 模型分别提取稳定和动态的空间相关性，能够更有效地捕获长时间范围内空间相关性的动态变化。这也表明，空间相关性在短期预测中可以简单视为不变，但是对于长期交通流预测任务，空间相关性的动态变化更为明显和重要。

图7 TSGCN 模型与基线模型在不同预测时间下的MAE 对比Fig.7 Comparison of MAE between TSGCN model and baseline models under different prediction time

5 总结与展望

本文提出了一种用于交通流预测的深度学习框架TSGCN。采用分解层对交通流数据的动态空间依赖性进行建模，将实时交通流数据分解为稳定分量和动态分量。然后，通过双流图卷积层分别从两个分量中分析稳定和动态空间相关性，以捕获更准确的空间相关性以进行动态交通预测。在两个公开的真实交通流数据集上，本文提出的TSGCN 模型优于最新的对比方法。可以证明从交通流数据的稳定和动态分量中提取空间相关性能更好地反映复杂交通流数据的动态变化，并为交通流预测提供更准确的信息。

在以后的工作中，将在交通预测中考虑特殊时间的时间依赖性，包括周末和节假日。此外，还将尝试将外部交通环境信息（例如事故数据和天气信息）引入交通流预测中。