格点插值计算面雨量方法的Python编程实现

李胜

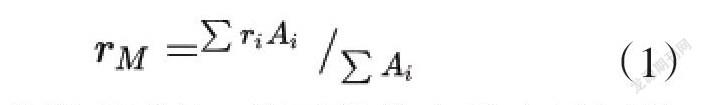
关键词：面雨量；格点；插值；射线法

中图分类号：TP311.1 文献标识码：A

文章编号：1009-3044（2022）36-0039-04

1 前言

近若干年来，随着全球气候变暖，极端天气气候事件呈现增多增强趋势。根据《WMO天气、气候和水极端事件造成的死亡和经济损失图集（1970—2019）》数据显示，50年间，全球共发生1.1万多起与天气、气候和水相关的灾害，共造成了200多万人死亡和3.64万亿美元的经济损失。中国是世界上受气象灾害影响最严重的国家之一，气象灾害所造成的损失占到了自然灾害损失的70%以上。因极端天气，特别是当暴雨、短时强降水等恶劣天气发生时，由于降雨过于集中很快造成大的地表径流，在城市或平原地区可能因排水不及时而产生大量的积水，致使土地、房屋等渍水、受淹而造成雨涝灾害。在山区，由于受地形阻挡作用，常常会形成绕流和爬流等，从而易诱发山体滑坡和泥石流等次生灾害。因此了解降雨区域内降雨总体情况十分必要。

面雨量从定义上讲是指计算统计区域内单位面积上降水量的平均值，能比较客观真实地反映某个区域的整体降水情况。面雨量是水利部门开展洪水预报非常重要的基础数据，开展面雨量计算能更好地为各级政府组织防汛抗洪以及水库涵闸调度、拦蓄泄洪等重大决策提供依据，在气象与水文水利部门的合作中发挥着十分重要的作用，是服务地方经济建设和防灾减灾工作的一个重要手段。

2 面雨量简介

气象学中常用的降雨量，是指一个气象观测站点上测得的可代表观测站点周围一个小区域的平均降水量，也就是通常所说的某地下了多大的雨。雨量是分布得极不均匀的一种气象要素，在大气候环境相似的条件下，山区雨量多于平原，高地雨量多于河谷低地。而对于江河湖泊来说，孤立的点状的雨量数据并不能代表整个流域的降雨情况，流域范围内单位面积上的平均降水量才能客观反映真实降雨情况[1]。

3 面雨量计算

用rM表示面雨量，用ri表示各点实测雨量，用Ai表示该点所代表的面积，面雨量的计算方法如公式（1）所示：

如果简单地求算术平均，是不能代表整个地区的真正面平均雨量的。于是，便发展了一些计算面雨量的方法。以不同的方法决定Ai，就得到不同的面平均雨量计算方法。面雨量常见计算方法有等值线法、数值法、算术平均法等。

3.1 等值线法

等值线法是以相邻两条等雨量线的平均值ri以及两线之间的面积Ai，代入公式（1）即可，但由于雨量等值线往往是不规划的曲线，用此方法计算两条曲线所包含区间的面积Ai，其过程相当复杂[2]。

3.2 数值法

数值法是指泰森多边形法或三角形法。泰森多边形法是将流域内每3个最靠近的雨量站连成一个三角形，流域边缘的站可利用流域外相邻的站来连接三角形。对三角形各边分别作垂直平分线，这些线组成若干个多边形，使得每个多边形内有且只有一个雨量站。每个多边形的面积为Ai，其雨量为ri，代入公式（1），便可求得rM。用此方法计算多边形面积Ai过程更加复杂和烦琐[3]。

三角形法如泰森多边形法那样，将相邻的3个站连成三角形。任意一个三角形的面积为Ai，3个顶点是3个站，雨量分别为ri1、ri2、ri3，3个雨量的平均值是ri，代入公式（1）即可。可见，三角形法相对于泰森多边形法来说，算法上要方便一些，但是计算过程依然烦琐。

3.3 算术平均法

算术平均法相对比较简单易行，将区域内所有站点的雨量计算其平均值即可。用此方法计算面雨量结果的可用性要依赖于区域内站点数量的多寡，而现实情况是区域自动气象站不可能特别密布，这就需要引入格点插值计算方法了。

3.4 格点插值

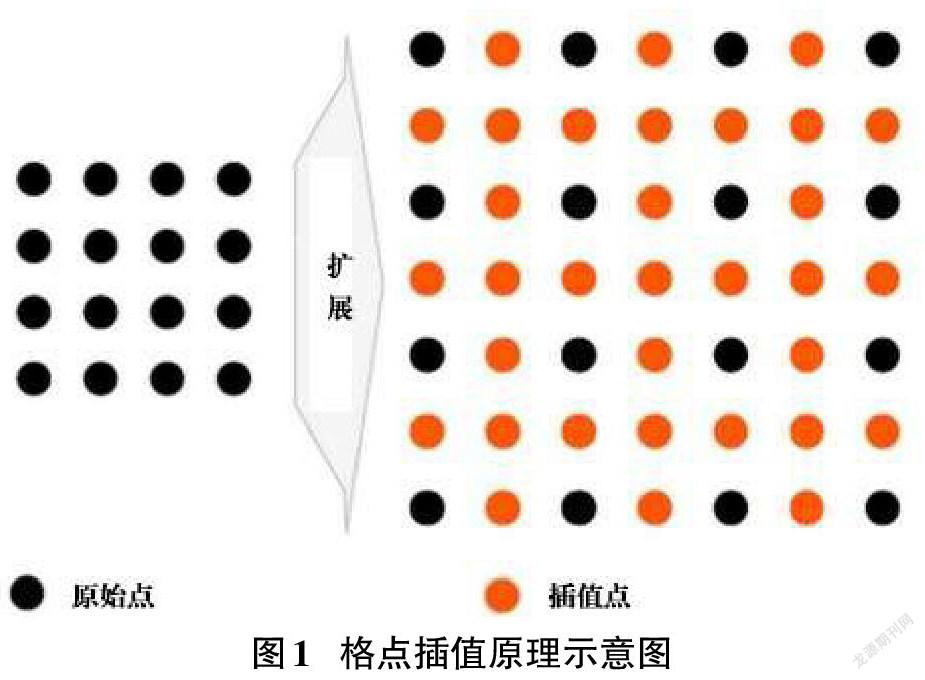
插值法是离散函数逼近的重要方法，即在一定的区域范围内按照一定的间隔，根据离散函数在有限个点处的取值状况估算出函数在其他点处的近似值[4]。其实现原理如图1所示。

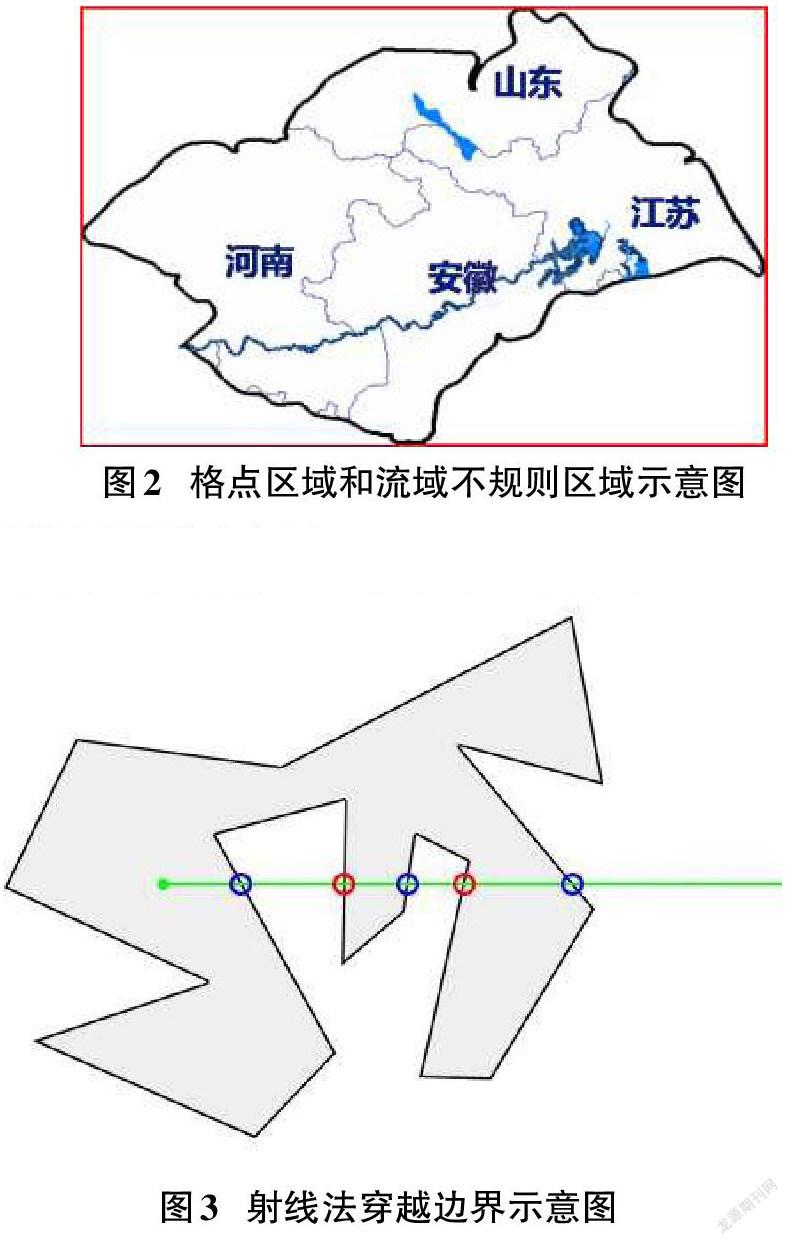
但是，由于格点插值计算的区域是取江河湖泊流域边界上下左右四個顶点所组成的区域（如图2红色外框所包围的区域），是规则的四边形，而实际江河湖泊流域边界是不规则的区间（如图2黑色线条所包围的区域），位于格点区域内，即被包含在格点区域内。因此要对计算出的所有格点进行判断是否位于不规则区间内，只有位于不规则区间内的格点才是计算面雨量所需要的。

3.5 射线法判断格点位置

通常采用射线法即用水平扫描线法或垂直线法即射线法来判断一点是否在区域内。在不考虑非欧空间的情况下，对于平面内任意闭合曲线把平面分割成了多边形区域内、外两部分。当射线穿越多边形区域边界时，要么是进入多边形区域要么是穿出多边形区域[5]。

如果某个点在多边形区域内部，射线第一次穿越边界一定是穿出多边形区域，当再次穿越边界一定是穿入多边形区域；如果某个点在多边形外部，射线第一次穿越边界一定是穿入多边形区域，当再次穿越边界一定是穿出多边形区域。如图3所示。

由于射线是由线段的一端无限延伸的直的线，而多边形区域的边界是固定的，因此射线最后一次穿越多边形边界，一定是穿出多边形，到达外部。假定某点在多边形外部，射线进入和穿出多边形至少需要零次或两次即偶数次才能到达多边形外部。假定某点在多边形内部，射线穿出或穿出、进入、再穿出多边形至少需要一次或三次即奇数次才能到达多边形外部。因此，由射线和多边形边界相交的次数是奇数还是偶数就可以推断出某点是在多边形内部还是在多边形外部。

4 格点插值编程实现

Python作为大多数平台上编写脚本和快速开发应用的编程语言，除自身提供丰富的标准库外，其解释器还易于扩展。NumPy（Numerical Python）是Py⁃thon最为重要的一个扩展模块，特点针对数组运算提供大量的数学函数库，常被用来做数组、矩阵甚至多维运算。其中的meshgrid函数功能是根据传入的两个一维数组参数生成两个数组元素的列表，即将两个一维数组生成一个二维矩阵，对应两个一维数组中所有的（x，y）对。scipy.interpolate是Python实现各种插值法的扩展模块，其griddata函数可以方便实现二维插值。插值方法有最邻近插值nearest、阶梯插值zero、线性插值slinear或linear、样条曲线插值quadratic或cu⁃bic，由于样条曲线插值让插值结果具有更好的平滑性，所以本文选用样条曲线插值[6]。

4.1 计算区域雨量格点值

根据前文面雨量算法思路，先计算出四边形格点，然后判断所有格点是否在不规则区间内，剔除在不规则区间外的格点后，即取得在不规则区间内的格点，最后计算这些剩余格点雨量的平均值，即是最终的面雨量。具体实现过程如下。

4.1.1 计算生成经纬度网格

先根据该区域的经纬度范围计算生成经纬度网格，再根据经纬度网格插值计算雨量的格点值。假定某区域内站点雨量实况文件内容如下（格式为经度，纬度，雨量）：

117.33，32.39，0

......

# 生成经纬度网格，其中minLon，maxLon，min⁃Lat，maxLat分别是某区域的最小经度、最大经度、最小纬度和最大纬度

LonLatArea=[minLon，maxLon，minLat，maxLat]

LonX=np. linspace（minLon， maxLon， int（（maxLonminLon）/经度分辨率））

LatY=np.linspace（minLat，maxLat，int（（maxLat-min⁃Lat）/纬度分辨率））

LonGrid，LatGrid=np.meshgrid（LonX，LatY）

4.1.2 插值计算出雨量格点值

# 先将雨量文件按行读取到列表PreTemp中，然后分别提取经纬度和站点雨量值到Points和Pres列表中

for i in range（len（PreTemp））：

line=str（PreTemp[i][0]）

preinfo=line.split（'，'）

Points. append（[float（preinfo[0]）， float（prein?fo[1]）]）

Pres.append（float（preinfo[2]））

# 根据经纬度网格插值计算出雨量格点值

PreGrid=griddata（Points， Pres， （LonGrid， LatGrid），method='cubic'，fill_value=0）

# 如果插值计算出的雨量小于0，则赋值为0

PreGrid[PreGrid<0]=0

4.2 判断边界内格点

根据射线法基本原理，假若有一疑问点P（x，y），要判断它是否在多边形内，可从该疑问点向左或向右引水平扫描线（即射线）并计算此线段与区域边界的相交次数c。如果c为奇数，认为疑问点在多边形内；如果c为偶数，则疑问点在多边形外。

假定某区域边界文件经纬度文件内容如下（格式为经度，纬度）：

117.40178，31.69473

117.40212，31.69395

......

117.40178，31.69473

4.2.1 判断坐标点是否在外包矩形内先要判断某个格点坐标是否在外包矩形内，即是否在minLon，maxLon，minLat，maxLat范围内，以便快速剔除多余格点，然后利用射线法判断是否在多边形范围内。

# poi是格点坐标，sbox是边界经纬度列表

def isPointInRect（poi，sbox，toler=0.0001）：

if poi[0]>sbox[0][0] and poi[0]<sbox[1][0] and poi[1]>sbox[0][1] and poi[1]<sbox[1][1]：

return True

if toler>0：

pass

return False

4.2.2 判断射线与边界是否有交点

# 判断点，边起点，边终点，都是[lon，lat]格式列表def isRayIntersectsSegment（poi，s_poi，e_poi）：

# 排除与射线平行、重合，线段首尾端点重合的情况

if s_poi[1]==e_poi[1]：

return False

# 线段在射线上边

if s_poi[1]>poi[1] and e_poi[1]>poi[1]：

return False

# 线段在射线下边

if s_poi[1]<poi[1] and e_poi[1]<poi[1]：

return False

# 交点为下端点，对应spoint

if s_poi[1]==poi[1] and e_poi[1]>poi[1]：

return False

# 交点为下端点，对应epoint

if e_poi[1]==poi[1] and s_poi[1]>poi[1]：

return False

# 线段在射线左边

if s_poi[0]<poi[0] and e_poi[1]<poi[1]：

return False

# 求交点

xseg=e_poi[0]-（e_poi[0]-s_poi[0]）*（e_poi[1]-poi

[1]）/（e_poi[1]-s_poi[1]）

# 交点在射线起点的左侧

if xseg<poi[0]：

return False

return True

4.2.3 判断格点坐标是否在边界内

def isPointInPoly（poi，poly，toler=0.0001）：

# 先判断格点坐标是否在外包矩形内，如果不在，函数返回False if not isPointInRect（poi，RectLatLon，toler）：

return False

# sinsc是交点个数

sinsc=0

# 對格点坐标进行判断是否在多边形范围内

for i in range（len（poly）-1）：

s_poi=poly[i]

e_poi=poly[i+1]

if isRayIntersectsSegment（poi，s_poi，e_poi）：

sinsc+=1

return True if sinsc % 2==1 else False

4.3 计算格点面雨量

将上述计算出的属于边界范围内的格点雨量进行算术平均即可求得面雨量。

# 提取并计算边界范围内的格点雨量

gribcnt=presum=0

for m in range（len（PreGrid））：

for n in range（len（PreGrid[m]））：

if isPointInPoly（[LonGrid[m][n]，LatGrid[m][n]]，

AreaPloy，toler=0.0001）：

presum+=PreGrid[m][n]

gribcnt+=1

PreAvg=round（presum/gribcnt，1）

5 结束语

由于不同的面雨量计算方法有不同的出发点和目标，也有其适用条件。在一定条件下有某一种方法比其他方法准确，因此不能笼统地说某种方法最好。随着气象部门观测站点安装越来越密集，站点布局不再是以往零散分布，也已呈现网格化，这些观测站点雨量数据再经格点插值后计算的面雨量可以很好地作为气象预报服务和水文水位预报的重要数据支撑。