基于常系数的Volterra生物数学模型稳定性分析
廖晓花
(闽南理工学院 信息管理学院,福建 石狮 362700)
随着科学技术的不断进步,对于生物科学的相关研究已经成为人类探索自然的重要途径之一.生物数学主要根据生物种群中的定量与定性关系建立不同形式的数学模型,通过对模型的求解进一步分析生物与数学之间的关系,从而能够更好地预测生物变化.
Volterra是生物数学领域重要的研究方法,此方法的提出象征着生物数学领域研究走进黄金时代,且到目前为止常微积分方程、偏微分方程等理论在生物学模型中广泛应用,使得该领域呈现繁荣发展态势,例如文献[1]中利用白噪声对生物数学模型的稳定性进行分析与反馈,通过环境白噪声分析生物数学模型中的增长率、环境容纳量、竞争系数等因素,并根据白噪声对生物数学模型稳定性进行图像转换,以此构建了一套不含噪声的外来入侵生物阶段结构模型.文献[2]在Volterra数学模型的基础上建立能够同时控制变量与系数的种群反馈系统,以静态关系与动态关系作为数学分析的临界条件,并在建立数学模型的过程中判断生物数学模型的立体空间平衡点,针对模型中的连续变化参数,研究病菌的持久性和灭绝性的相关因素.
本文采用常系数对Volterra生物数学模型稳定性进行分析,通过常系数进一步分析Volterra生物数学模型中的潜在关系与相关生物变化特征.
1 具有脉冲种间关系的Volterra生物数学模型
具有脉冲种间关系的Volterra生物数学模型中种间相互作用关系如公式(1)所示
(1)
生物数学模型中种间关系具有偏利性的相互关系,可以表示为
(2)
公式中,z≥0、y≥0、k1≥0、k2≥0、a≥0,其中r1和r2分别代表两个不同规模的种群数量,z和y分别代表两个种群的生物增长率,k代表不同种群的环境最大容纳量,a代表在种群内的每个种群个体对环境的作用.在生物竞争的环境中各个生物种类均为有利种群且受到生物环境的影响.
以上两个Volterra生物数学模型中的生物种群偏利共生关系能够保持一定的持续性,而实际的生态环境中则会由于外界原因导致生物数学模型中的常系数发生永久性变化,产生具有脉冲效果的固定形式种群关系模式如下
(3)
公式中,r、k、n和υ均大于0,z和y分别为常系数Volterra生物数学模型相关算法的解,且z和y分别为模型中种群数的不变集合,每一个非负数解都能够满足常系数下的Volterra生物数学模型种群全局性正解.在生态系统中为了保障生物种群的多样性,需要对生态环境中每个生物种群中的增长率进行判断,以解决生物可持续性与稳定性发展过程中存在的一系列问题[3-5].本文首先应用常系数分析脉冲种间关系的Volterra生物数学模型中的永存定理,其求解公式如下
(4)
公式中,u、r、d、t等种群内系数均大于0,在此过程中获取的解存在严格意义上的正解与负解,公式中存在正解说明在目前的生态环境下种群z和y分别在最大容纳量的边界浮动,在不超出环境最大容纳量的情况下,两种物种的种群发展将会实现可持续生存发展;而公式出现负解的情况则说明在目前的生态环境下两种物种种群的发展呈现竞争状态,且有一个种群的发展曲线逐渐偏离最大容纳量,两个种群的持续发展呈现不平衡状态,这两个种群将不能实现持续性发展[6-7].
对于常系数下的Volterra生物数学模型中生态环境的研究,人们更加注重生态系统中生物种群的渐进性行为,两个种群在生态环境中的共生形式能够利于Volterra生物数学模型的常系数周期获取,在Volterra生物数学模型中确定常系数n、s和d,则有
(5)
若公式(5)成立,则证明两种群在目前的生态环境中无论处于何种生存状态,种群z和y将呈现持续性发展与归一性发展,这种生存状态在自然界中是一种较为普遍的方式[8-10].常系数下的Volterra生物数学模型生物种群的不同发展趋势曲线如图1所示.
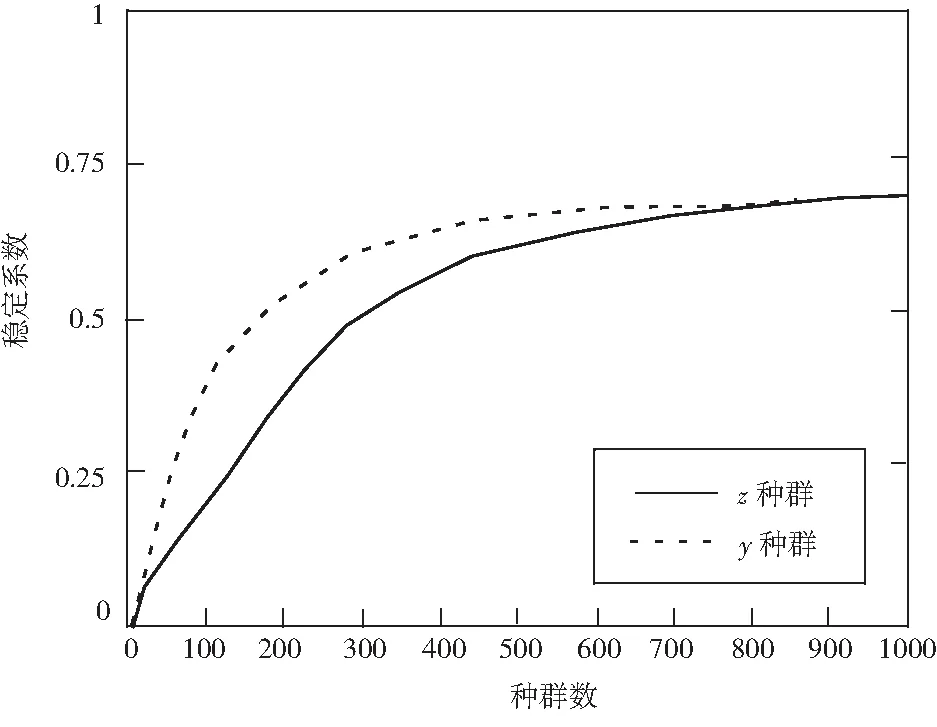
图1 Volterra生物数学模型生物种群的不同发展趋势
2 模型稳定性分析
生态系统中存在着生命周期较短的生物种群或生命周期过长的生物种群,对这两种生物种群进行定性分析.本文主要利用常系数对Volterra生物数学模型中的离散性与耦合性变化关系进行分析[11-12].时滞离散型模型为
(6)
此模型中z种群与k增长率系数能够反映时滞离散型模型中生物种群动力学关系.其中,生物种群死亡周期与该种群的增长率、数量呈现正比线性关系,通过线性关系分析能够获取离散模型中的种群生物周期的稳定性,常系数临界点状态下种群的发展线形图如图2所示.

图2 常系数临界点状态下种群的发展线形图
随着种群数量的不断增长,具有周期性特征的生物种群增长率逐渐平衡,根据差分理论方程的稳定性基本理论得出常系数下的Volterra生物数学模型中周期性种群的稳定性条件以及特征方程在曲线图中的分布,常系数临界点状态下种群的相轨线如图3所示.
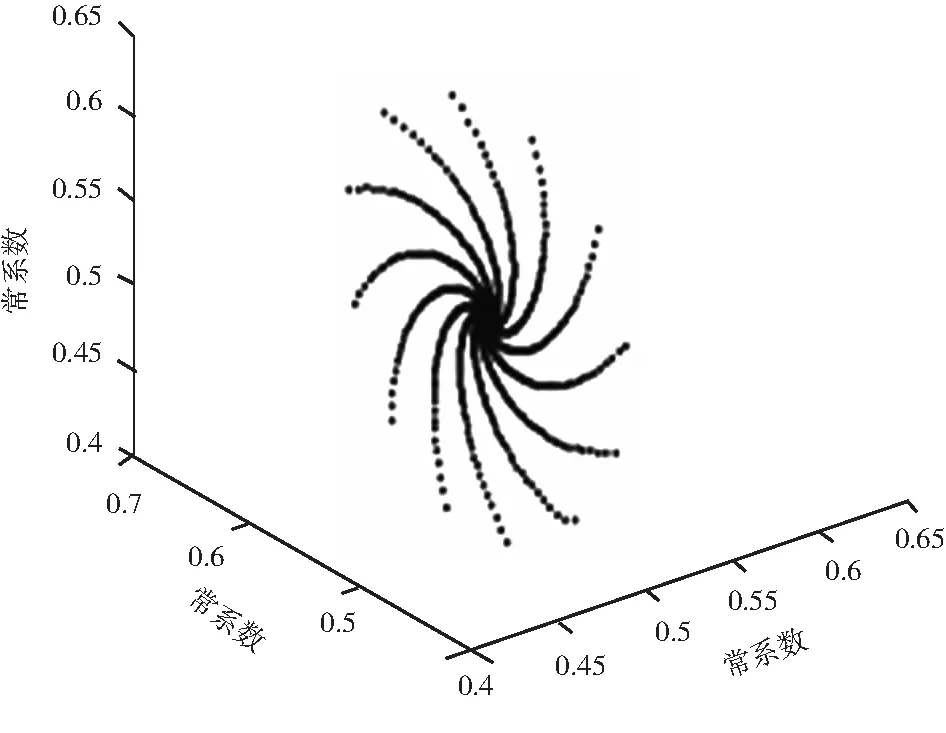
图3 常系数临界点状态下种群的相轨线
Volterra生物数学模型中的输入量与输出量存在着相互作用的关系,因此Volterra生物数学模型表现出时滞耦合现象[13].在生态系统中生物种群存在着捕食、竞争、互利共生等种群关系,分析不同关系下的模型的稳定性.本文将用常系数对Volterra生物数学模型进行更改,通过常系数控制Volterra生物数学模型中空间平衡点,在稳定性分析前期需要确定不同种群的捕食率,再确定不同种群的成熟期与死亡周期,之后采用常系数进行运算,从宏观的角度分析整个生态环境中生物种群的死亡趋势与生长趋势.在Volterra生物数学模型中取不同的平衡点进行计算分析,获取平衡点与种群周期趋势较稳定的常系数,得到不同种群的相轨线如图4所示

图4 不同种群的相轨线
通过具有时滞性的耦合Volterra生物数学模型获取生态系统中的稳定平衡点,对不同物种的发展趋势线性化处理,进而得到常系数下的模型稳定性分析结果[14-15].
3 实验研究
为验证基于常系数的Volterra生物数学模型稳定性方法的效果,通过模拟实验验证该方法的性能.
选择传统的基于动力学状态的生物数学模型稳定性分析方法与基于捕获模型的Volterra生物数学模型稳定性分析方法与本文提出的基于常系数的Volterra生物数学模型稳定性方法进行实验对比.
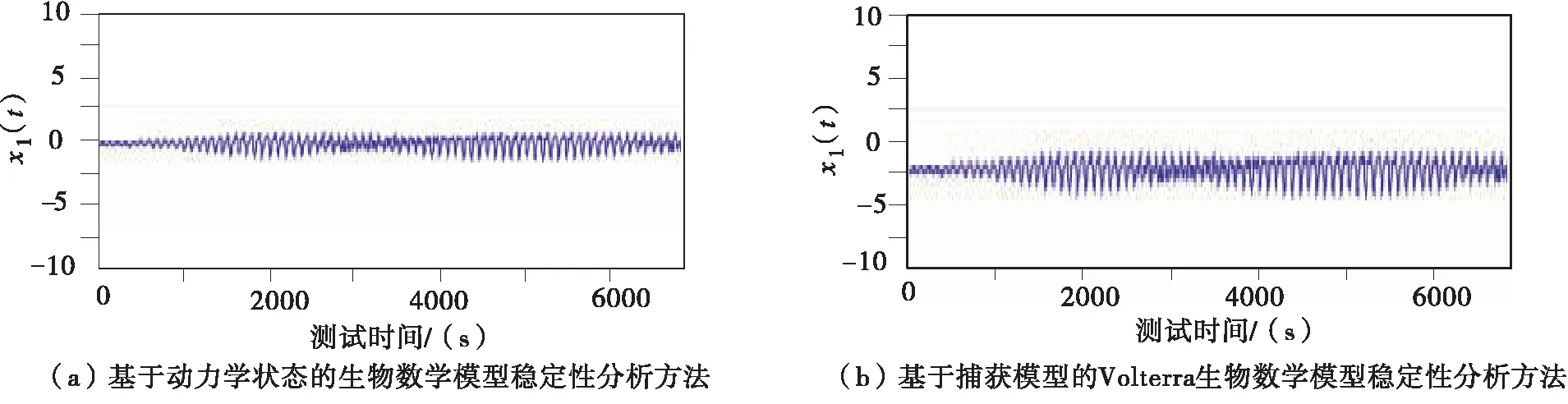
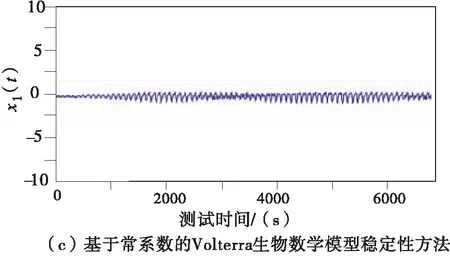
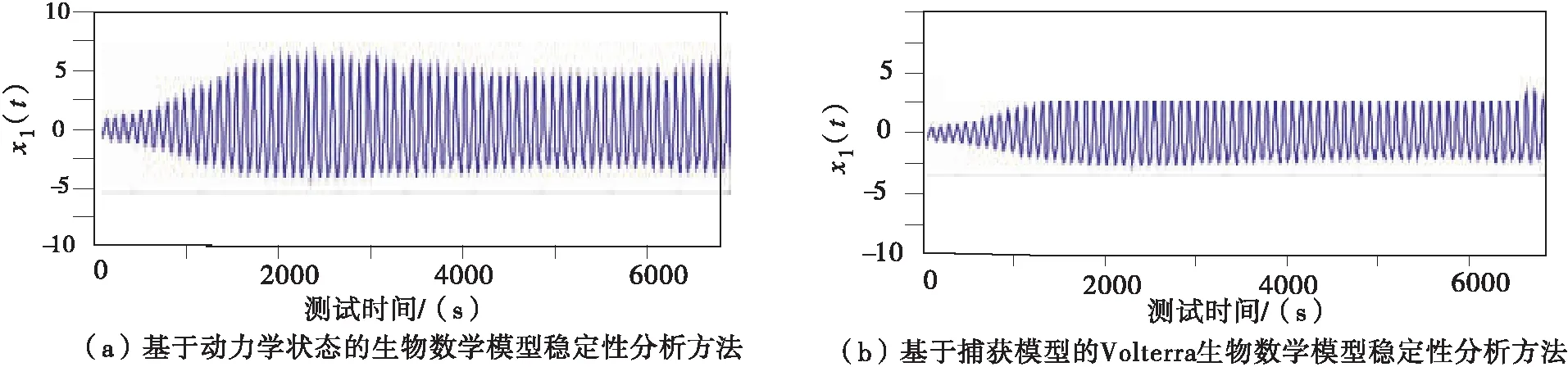
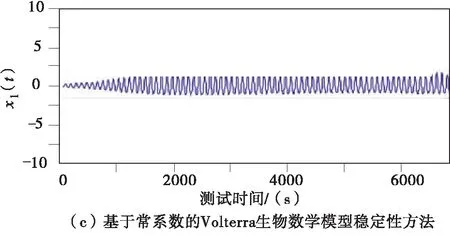
寻找两种偏离种群,种群分别为x(t)和y(t),设定脉冲条件为r=k1=k2=1,则可以证明每隔一段时间种群就会收获一次.比例系数0 当生物系统规模取值为(0.9,0.4)时,不同分析方法得到的稳定性曲线不同,其中生物系统的X序列值如图5所示. 图5 生物系统内部X时间序列图 生物系统的Y序列值如图6所示. 图6 生物系统内部Y时间序列图 分析图5和图6可知,本文提出的基于常系数的Volterra生物数学模型稳定性方法得到的X时间序列图和Y时间序列图数值小于传统方法. 根据生物系统内部X时间序列图和Y时间序列图得到不同种群的稳定性,为更好地确定模型稳定性,本文针对三个种群进行研究,种群分别为x1(t)、x2(t)和x3(t),x1(t)稳定性效果如图7所示. 图7 x1(t)稳定效果图 观察图7可知,传统方法在判定稳定性时,会出现一定的脉冲效应,本文提出的基于常系数的Volterra生物数学模型稳定性方法由于能够分析固定时刻脉冲关系,所以该方法更稳定. x2(t)稳定效果如图8所示. 图8 x2(t)稳定效果图 分析图8可知,在种群为x2(t)时,本文研究的方法稳定性更高,能够精准地分析不稳定的鞍点,能够有效实现对成熟周期进行判定,防止外界干扰,保证分析结果的准确性. x3(t)稳定效果如图9所示. 图9 x3(t)稳定效果图 分析图9可知,本文提出的基于常系数的Volterra生物数学模型稳定性方法的分析效果更好. 在不同种群中,本文提出方法和传统方法都能够进行Volterra生物数学模型稳定性分析,但是不同方法的分析能力不同,这种差异在x1(t)分析方面体现得作为明显,x2(t)其次,x3(t)分析效果差异最弱. 传统的分析方法虽然也能够分析模型稳定性,但是由于会受到外界干扰,所以分析结果准确率较低.而本文提出的稳定性分析方法不仅可以分析脉冲模型,确定噪音,还可以通过剔除噪音提高稳定性分析结果的准确性. 为解决目前存在的生物数学模型稳定性分析方法存在的分析效果较差的问题,本文提出了一种基于常系数的Volterra生物数学模型稳定性分析方法.通过确定脉冲种间关系,建立时滞性离散和耦合Volterra生物数学模型,从而确定该模型的稳定性.实验分析结果表明,本文提出的分析方法能够精准地获得时间序列,从而提高分析结果的准确性.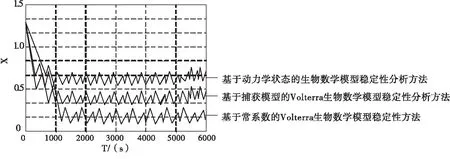



4 结束语

