一种求解信赖域子问题的多割线折线算法

李 亮

(华中师范大学附属息县高级中学，河南 息县 464300)

在无约束优化问题的研究中，信赖域算法不仅具有较好的可靠性，而且具有较强的收敛性，受到无约束优化研究界的高度重视，成为优化研究界的一个研究热点.

无约束优化问题如下

minf(x),x∈Rn,

(1)

其中f(x)∶Rn→R是目标函数，x∈Rn是待求变量.

因为信赖域算法求解无约束优化问题(1)时，每步迭代都必须求解如下形式的信赖域子问题

(2)

其中，g∈Rn为目标函数f(x)在当前迭代点的梯度,B∈Rn×n为目标函数f(x)在当前迭代点的Hessian矩阵，Δ∈R为信赖域半径，δ∈Rn为待求变量.所以信赖域子问题(2)的求解在信赖域算法中至关重要.

目前已经提出了很多求解信赖域子问题(2)的方法，比如赵英良等[1]提出的切线单折线法，赵丹[2]提出的混合折线法,陈争等[3]提出的光滑牛顿法,王希云等[4]提出的双割线折线法，李亮等[5]提出的分段割线法,文献[6]提出的隐式分段折线算法,文献[7]提出的分段切线算法,文献[8]提出的改进的隐式Euler切线法，贾新辉等[9]提出的改进的平均欧拉切线法，武姝廷等[10]提出的基尔方法等.

定理1[11]δ*是信赖域子问题(2)的解,当且仅当存在μ*≥0,使得如下方程组成立

(3)

而且(B+μ*I)是半正定矩阵.

24例动脉瘤患者中CT扫描结果，小型动脉瘤（＜5mm）7例，中型动脉瘤（5～10mm）12例，大型动脉瘤（11～25mm）4例，巨大型动脉瘤（＞25mm）1例，24例动脉瘤中21例存在破口。

由定理1可知，信赖域子问题(2)的精确求解方法即是求解如下方程组

(4)

利用牛顿法[11]求解方程组(4)的步骤

当μ=0时,则取δ*=-B-1g；

因此为了更精确的求解非线性方程φ(μ)=0的近似根，本文利用线性插值法[12]构造了一条多割线折线，并提出了一种求解信赖域子问题的多割线折线算法.

1 多割线折线的构造

对插值节点(μk,yk)，k=0,1,2,…,M采用文献[12]中的线性插值法构造M条直线,每条直线对应的一次函数记为lk(μ),k=1,2,…,M.把构造的M条直线连接起来构成一条多割线折线，符号记为L=[y0,y1,…,yM].

2 多割线折线路径的性质

定理2记多割线折线L=[y0,y1,…,yM]对应的分段函数如下

(5)

则L(μ)满足

①L(μ)为连续单调增函数.

3 算法描述

解信赖域子问题(2)的多割线折线算法的步骤为

步1 给定梯度g,正定矩阵B,信赖域半径Δ，步长h.

步3 令μk=kh，计算yk=f(μk).

4 数值结果

采用文末附录中的测试函数，令多割线折线算法中的步长h=0.1，文献[7]中的欧拉切线算法步长中的参数k=8，然后进行数值实验，把多割线折线算法求解的测试函数在最优解处的函数值分别与文献[1]中的切线单折线法和文献[7]中的分段切线算法求解的测试函数在最优解处的函数值进行比较,并对数值实验结果进行了分析.数值实验结果分别列在表1和表2中,其中Δ表示信赖域半径，fTDL表示切线单折线法求解的测试函数在最优解处的函数值，fSTA表示分段切线算法求解的测试函数在最优解处的函数值，fMSD表示多割线折线算法求解的测试函数在最优解处的函数值.哪种算法求解的测试函数在最优解处的函数值越小，则表明该算法越好.

表1 测试函数1的数值结果

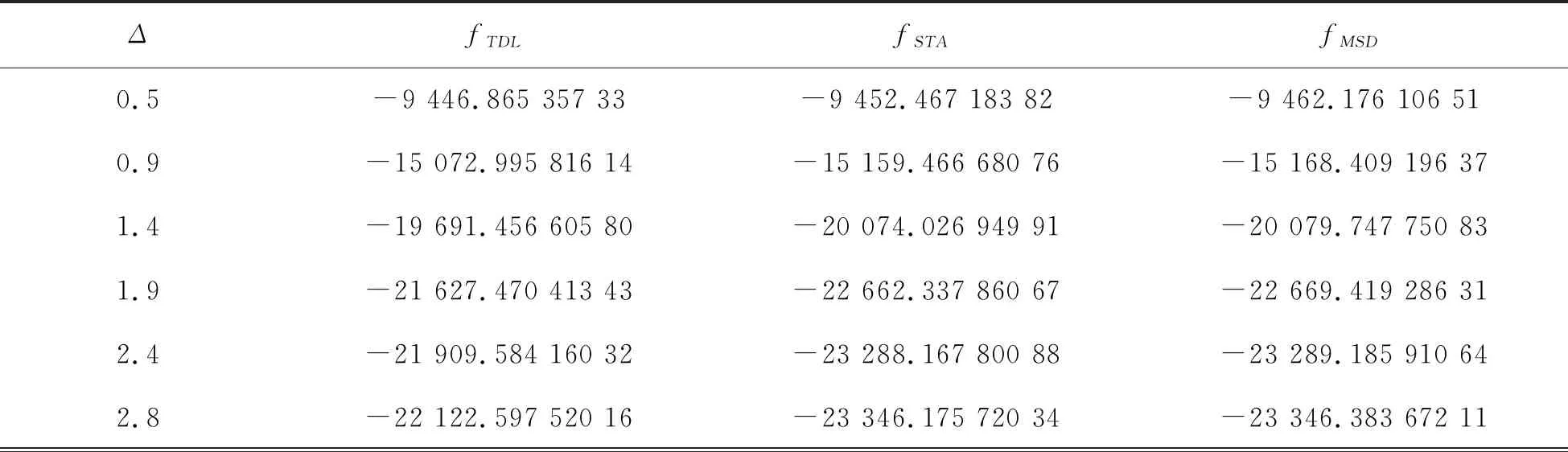
表2 测试函数2的数值结果

ΔfTDLfSTAfMSD3.3-22 316.032 885 48-23 386.275 745 38-23 386.343 192 643.8-22 476.231 429 06-23 416.650 080 99-23 416.680 881 784.3-22 616.807 965 29-23 442.274 587 55-23 442.290 486 984.9-22 766.971 341 43-23 469.004 596 76-23 469.013 302 355.3-22 857.938 076 34-23 484.974 157 06-23 484.979 317 365.7-22 942.494 095 14-23 499.702 926 65-23 499.706 710 636.3-23 058.353 283 21-23 519.738 899 23-23 519.741 167 526.8-23 145.533 588 69-23 534.723 779 98-23 534.725 140 857.3-23 224.657 041 60-23 548.266 788 91-23 548.267 101 817.8-23 296.024 927 90-23 560.440 991 88-23 560.440 577 388.2-23 347.685 789 06-23 569.231 407 96-23 569.230 780 988.7-23 405.613 330 47-23 579.067 428 40-23 579.067 194 459.2-23 456.277 227 86-23 587.653 114 57-23 587.652 425 549.8-23 507.631 575 85-23 596.339 869 59-23 596.339 256 5510.2-23 536.210 666 68-23 601.167 162 89-23 601.166 927 6810.7-23 565.629 335 18-23 606.130 751 82-23 606.130 397 9611.2-23 588.091 984 84-23 609.916 574 35-23 609.916 169 1011.8-23 605.926 946 85-23 612.919 381 27-23 612.919 310 3912.3-23 613.231 507 39-23 614.148 100 54-23 614.148 073 09≥12.59-23 614.333 333 33-23 614.333 333 33-23 614.333 333 33

文中所用测试函数如下