类蜂窝夹层结构振动特性分析及应用研究

陈永清，仇琨，李响

类蜂窝夹层结构振动特性分析及应用研究

陈永清1,2，仇琨2，李响1,2

（1.三峡大学 水电机械设备设计与维护湖北省重点实验室，湖北 宜昌 443002；2.三峡大学 机械与动力学院，湖北 宜昌 443002）

对新型类蜂窝夹层结构进行了振动特性研究，运用Hoff理论对类蜂窝夹层结构进行振动特性分析，计算类蜂窝夹层结构在四边简支边界条件下的振动固有频率方程解。并用有限元软件ABAQUS进行振动模态分析与理论值进行对比，结果表明误差保持在10%以内，吻合度较好，检验了理论公式的可行性。在此基础上研究类蜂窝夹芯壁厚和面板与夹层板厚度比等结构参数对类蜂窝夹层结构固有频率的影响。进一步研究类蜂窝夹层结构的优良性，在蜂窝夹芯胞元数量、材料、边界约束以及其他相关参数相同的条件下，与六边形和正方形蜂窝夹芯结构相比，仿真结果表明：根据蜂窝夹芯结构的整体振动固有频率和振动位移等仿真数据，可知类蜂窝夹层结构的性能更好，并与某型号电动车车身零件频率对比，由仿真数据表明：可应用在此车底盘甲板中。振动分析对未来的蜂窝夹层结构设计具有重要意义，扩展了蜂窝结构在工程振动方面的应用。

类蜂窝夹层结构；固有频率；夹芯壁厚；模态分析

蜂窝夹层结构材料具有高密度、轻质量、隔声、隔热等优良性能，用途广泛，比如在纸箱内运用可极大增强它的抗弯能力同时又减轻纸箱的重量；在交通运输工具、飞机航天等领域中，运用在动车车厢、小汽车底板等，可使动车的运行速度极大提高，也可使汽车的整体稳定性能加强。但汽车运行的时侯使汽车内的类蜂窝夹层结构振动，会对小汽车车身稳定性产生影响，甚至危害自身和汽车的安全，所以对类蜂窝夹层结构进行振动特性研究非常必要。Jack[1]提供了几种夹层结构的设计方法，包括夹层板理论、各向异性理论、层压板理论，以三明治结构为研究对象，考虑蜂窝夹芯剪切的影响，分析三明治壳的振动问题。Zhi-jia Zhang 等[2]主要对蜂窝波纹混合芯夹层梁进行模态性能研究，通过实验和有限元仿真技术分析它的振动特性问题，相关实验和有限元仿真结果表明：频率参数对面板厚度，夹层板相对密度参数影响不大，但是对微穿孔结构有影响，微穿孔直径越大，夹层结构的频率参数呈线性下降。Cetkovic等[3]考虑到横向剪切应力的连续性，运用广义层合板理论对夹层结构的振动问题进行研究，用公式推导了复合材料层合板振动问题的有限元解，在夹层板的离散模型等研究领域作出了重要贡献。Lok等[4]以薄壁桁架夹芯夹层结构为分析对象，计算桁架夹芯板的弹性常数，用双级数三角函数的方法研究厚板夹层板的振动响应问题，并讨论了剪切应变对板厚的影响。Chandrashekhar等[5]主要是进行非线性振动特性分析，考虑沿板厚的横向剪切均匀变化和材料性质的不同，分析了板的线性和非线性固有频率的区别。Reddy J. N[6]主要是研究关于复合材料夹层结构的几种剪切理论对振动频率的不同影响，考虑纵向板厚的抛物线型分布，并分析了一阶剪切变形理论对应力的影响，给出了剪切修正系数，用高阶剪切理论对振动频率的研究结果更为准确。Raville[7]主要是介绍了简支夹层结构自由振动时的实验过程和实验结果，其中忽略了受迫频率的影响，两者有较高的一致性，并分析了夹层结构横向振动的一般性及类蜂窝夹芯材料的面内异性，对以后在振动模态实验方面的研究有重要意义。中科院力学所[8]主要以弹性理论为文章理论依据，考虑了蜂窝夹芯同性或异性、弹性模量和剪切模量的不同、表面弯曲刚度的变化及夹芯的横向变形和其他力学因素等参数影响，分析实体板、弯曲板及蜂窝夹层直板的振动问题，对未来在蜂窝振动特性方向的研究有进一步的完善。卢翔等[9]主要以双层蜂窝夹层结构为分析对象，考虑振动固有频率的计算准确度和夹层板的不同叠加方式的影响，运用逐层理论和三维实体法建立夹层结构上、下面板的振动控制方程。吴晖[10]主要以波纹型夹层结构为分析对象，运用线性微分算子等简便计算方法，考虑纵向压力的作用和夹芯结构横向剪切力的影响，得出纵向压力与夹层结构振动特性之间的相互关系。李响[11]也对波纹夹层结构进行分析研究，考虑了面板夹角大小和夹芯放置方式不同的影响。经验证，与传统波纹夹层结构相比，该结构有更好的性能，夹芯角度变小其性能提升。夹芯纵向放置时可使夹芯结构的变形变小，更加稳固。为波纹夹层结构方面的研究开扩了方向。

综上对不同蜂窝结构进行了分析，本文对李响等[12]提出的新型类蜂窝夹层结构进行振动特性分析，如图1、图2所示。运用Hoff理论对类蜂窝夹层结构进行振动分析，给出了各向同性类蜂窝夹层结构振动固有频率的方程解，并做了关于类蜂窝夹层结构的仿真分析。分析壁厚大小等主要设计参数对类蜂窝夹层结构固有频率的影响，扩展了类蜂窝夹层结构在工程方面的应用。

图1 类蜂窝夹层板结构

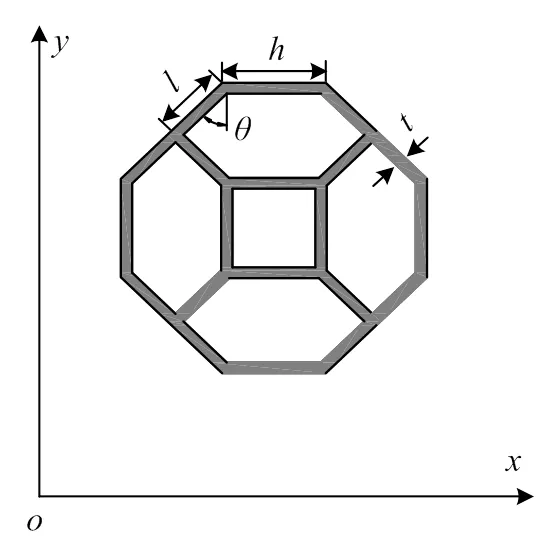
l为类蜂窝夹芯的斜边长的一半，mm；为类蜂窝夹芯的边长，mm；t为夹芯厚度，mm；θ＝45°。

1 类蜂窝夹层板的自由振动控制方程

图3为夹层结构等效示意图。根据Hoff理论，可给出以下基本假设[8]：

（1）面板层与蜂窝夹芯层相比长度较小，所以被当作薄板；

（2）类蜂窝夹芯相对较软，仅考虑夹芯结构的剪切变形。

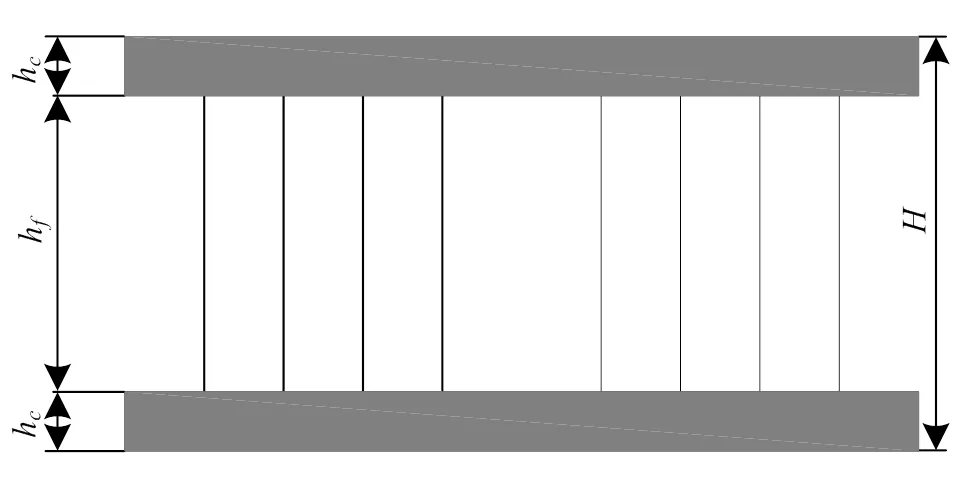
hc为类蜂窝夹层结构上、下面板的厚度，mm；hf为夹芯层的厚度，mm；H为类蜂窝夹层结构总体高度，mm。

弯矩、剪力与广义位移之间的关系为：

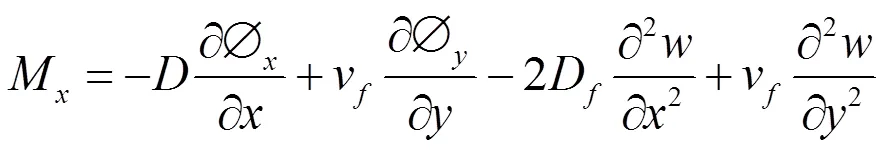
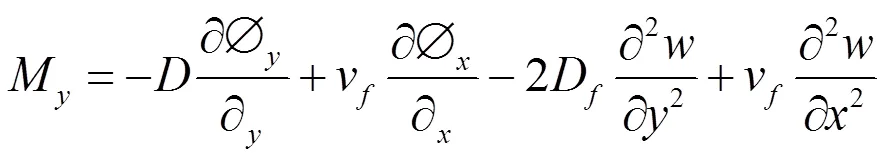
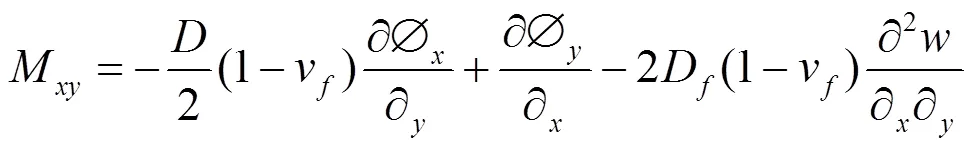
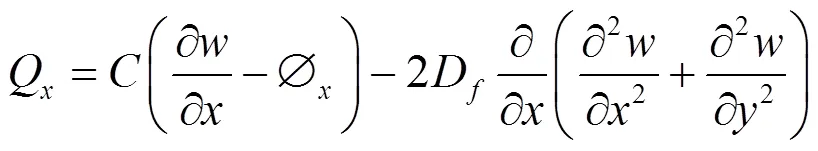
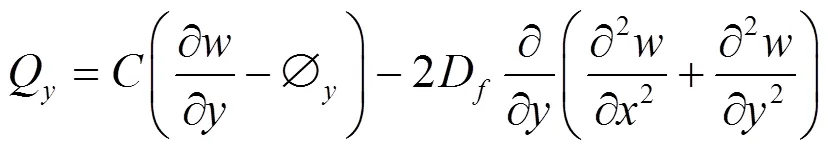
运动方程为：

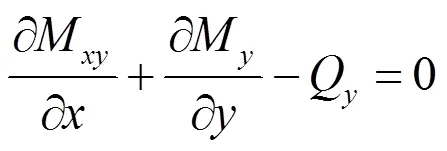
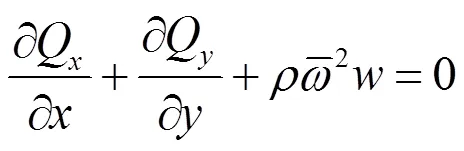
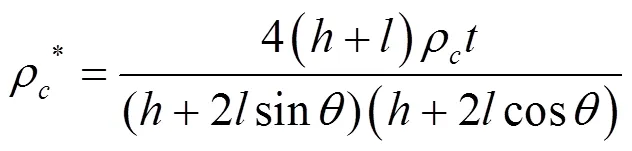
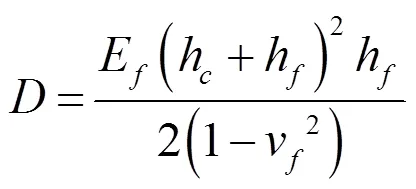
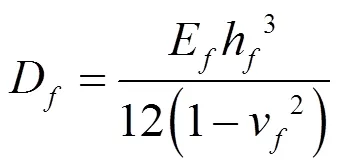
前列腺液中锌离子、PSA及MIP-1α水平与慢性非细菌性前列腺炎患者症状的相关性………………………………………………………………………… 罗 琳，等(7):802

将式（1）～（5）代入式（6）～（8）中，得类蜂窝夹层结构的振动控制方程组为：

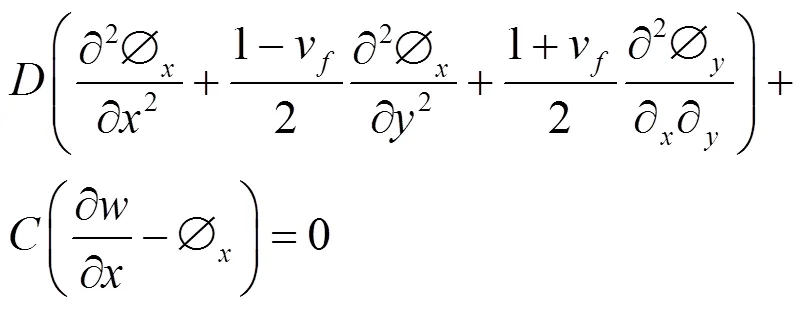
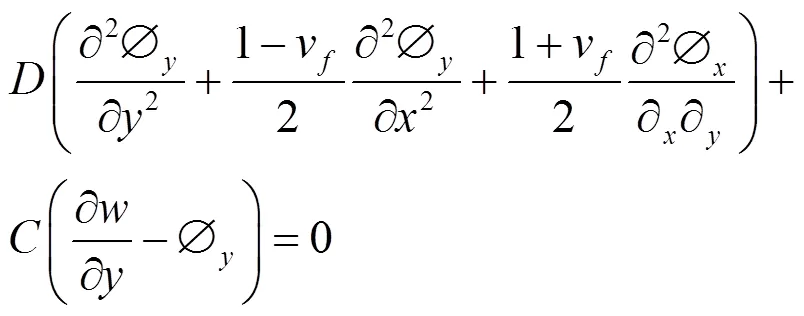
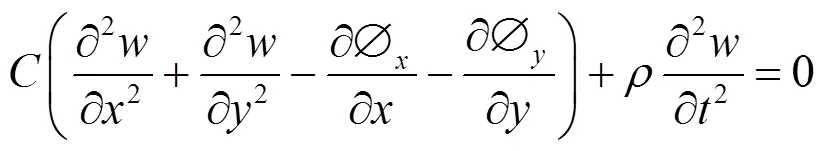
对方程组进行简化，得：

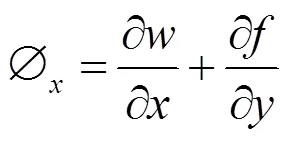
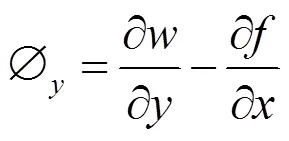
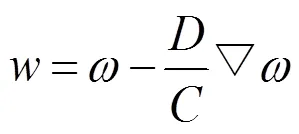
将式（12）～（14）代入式（11）中，得夹层结构振动基本方程为：

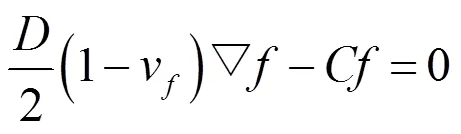
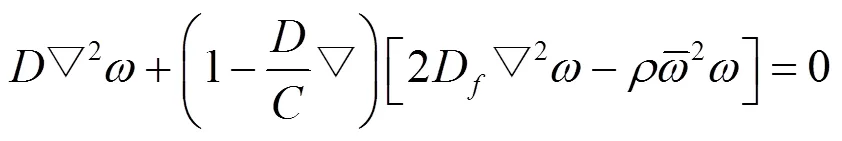
四边简支类蜂窝夹层结构如图4所示，其边界条件为：

＝0，时：

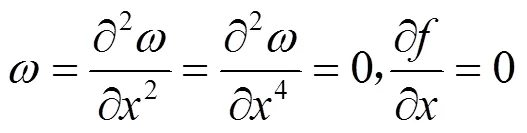
＝0，时：

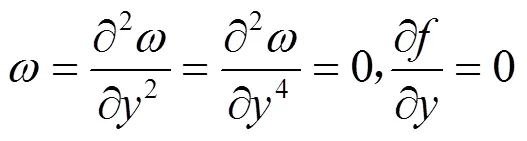
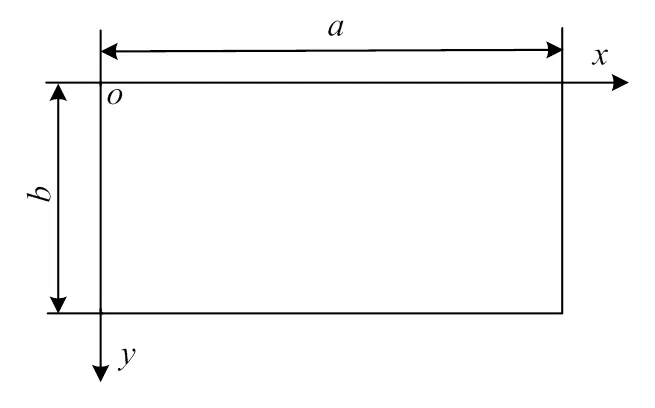
a为上、下面板的长度，mm；b为上、下面板的宽度，mm。

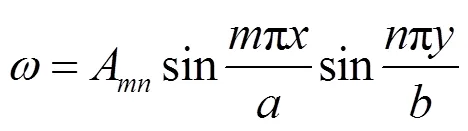
式中：，为频率的阶数，＝1，2，3…，＝1，2，3…

类蜂窝夹层结构振动控制方程为：

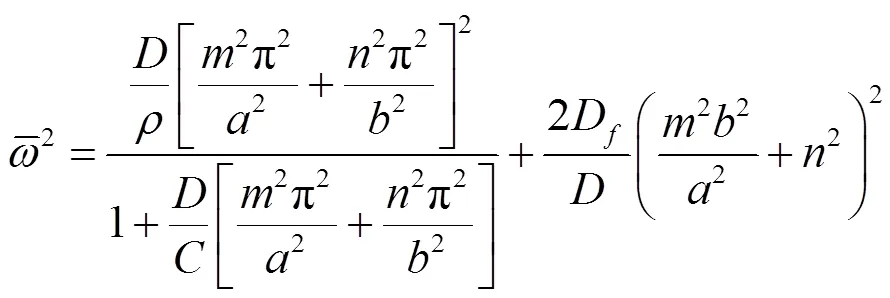
2 类蜂窝夹芯结构的模态分析

为检验本文方法的可行性，采用本课题组李响文中的填充新型类蜂窝夹芯结构的电动车底盘中部甲板的结构[14]。用仿真软件ABAQUS对四边简支边界条件下的类蜂窝夹层结构进行振动分析。类蜂窝夹层结构尺寸如表1所示。材料采用铝合金，密度约为2.78×103kg/m3，弹性模量E＝72400 MPa，泊松比v＝0.3。

图5是类蜂窝夹层结构的前4阶模态图，由有限元仿真结果可知：四边简支条件下类蜂窝夹层结构固有频率的理论结果与ABAQUS仿真模拟结果进行比较，如表2所示，使用ABAQUS仿真和公式计算的方法得到的数据差值在10%以内，一致性较好，检验了理论公式的可行性。

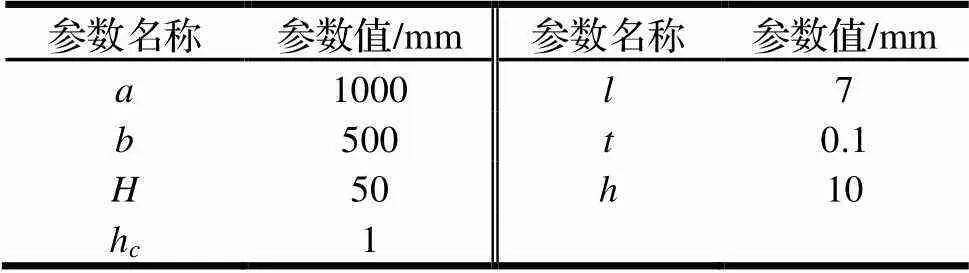
表1 类蜂窝夹层结构有限元模型几何参数

表2 类蜂窝夹层结构固有频率理论计算结果与有限元模拟结果对比

3 夹层板主要设计参数对固有频率的影响

研究夹芯壁厚和面板与夹层板厚度比h/对类蜂窝夹层板固有频率的影响，类蜂窝夹层板材料用的是铝合金材料。类蜂窝夹层结构整体尺寸为：

××＝1000 mm×5000 mm×50 mm

3.1 夹芯壁厚对类蜂窝夹层结构固有频率的影响

仿真结果如表3所示，类蜂窝夹芯壁厚大小在0.5～2.5 mm内变化时，类蜂窝夹层结构的振动固有频率随夹芯壁厚变化的曲线。

由表3可知：保证类蜂窝夹层结构的蜂窝长度、面板大小、夹芯厚度等参数数据不变。改变壁厚的大小，当类蜂窝夹芯壁厚增加时，类蜂窝夹层结构一阶频率依次减少，这是由于增加类蜂窝夹芯壁厚的同时增加了类蜂窝夹层的剪切刚度和夹芯质量，而一阶频率对类蜂窝夹层板质量的影响更为显著。除一阶频率之外，其它各阶固有频率随着类蜂窝夹芯壁厚的增加而提高，由仿真结果图可知：高阶固有频率比低阶固有频率变化幅度更加明显。

3.2 面板与夹层板厚度比hf/H对类蜂窝夹层结构固有频率的影响

仿真结果如表4所示，类蜂窝面板与夹层板厚度比h/在0.005～0.015内变化时，类蜂窝夹芯厚度h随之调整使其整体结构参数不变。类蜂窝夹层结构固有频率随h/变化的曲线。由表4可知，保证其他数据参数不变，改变面板与夹层板厚度比h/，随着h/的增加，类蜂窝夹层结构的一阶频率随之缓慢上升，因为随着面板与夹层板厚度比的增加，弯曲刚度和剪切刚度也随之增加，但是夹层质量几乎不变。除一阶频率之外，其它各阶的固有频率随面板与夹层板厚度比h/的增加逐渐减少。由仿真结果图可知，高阶固有频率相比一阶的变化幅度更大。

由以上振动理论及有限元仿真数据可知：保证其它数据参数不变，影响类蜂窝夹层结构的固有频率及振动模态的主要因素是面板与夹层板厚度比，夹芯壁厚，等效剪切模量。

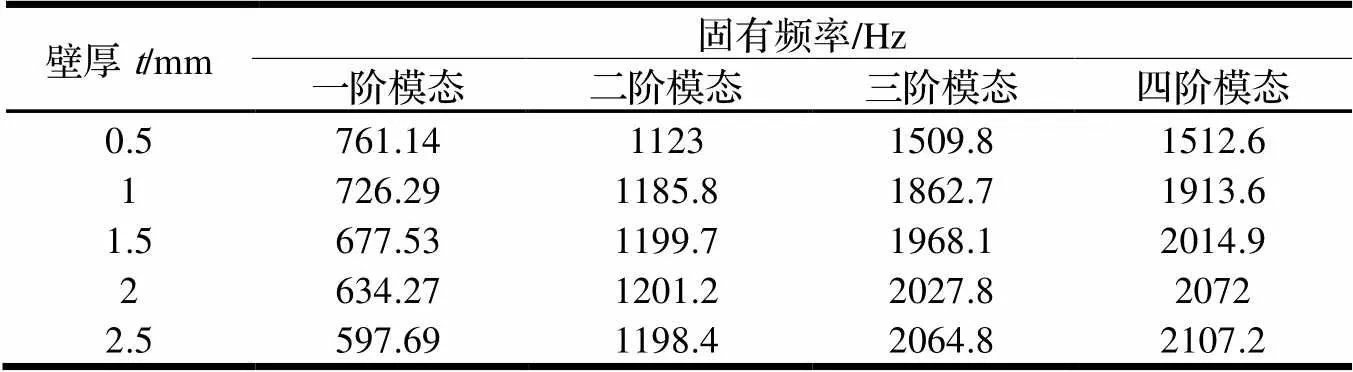
表3 类蜂窝夹芯不同壁厚时的固有频率对比

表4 类蜂窝面板与夹层板厚度比不同时的固有频率对比

4 与不同类型蜂窝夹芯对比

为了进一步验证类蜂窝夹芯的振动特性，将类蜂窝夹芯结构、正方形蜂窝夹芯结构和六边形蜂窝夹芯结构进行仿真模拟对比分析，为了便于比较，在数据参数及仿真设置相同的条件下与类蜂窝夹芯结构对比，进行振动模态分析后得到正方形蜂窝夹芯和六边形蜂窝夹芯的振动模态图。三种蜂窝夹芯的模态分析图如图6所示，三种蜂窝夹芯结构前六阶固有频率如表5所示。

从图6可知，在四边简支条件下进行振动模态分析，当产生振动时正方形蜂窝夹芯结构的面内破坏程度较大，六边形蜂窝夹芯和类蜂窝夹芯面内破坏程度较小。但是由有限元仿真数据可知，六边形蜂窝夹芯产生振动时最大位移是39.4 mm，而类蜂窝夹芯产生振动时最大位移是28.0 mm。从表5中三种夹芯结构前6阶固有频率的对比可知，在相同的情况下，类蜂窝夹芯结构的前6阶固有频率整体上大于其余两种类型的蜂窝夹芯结构。

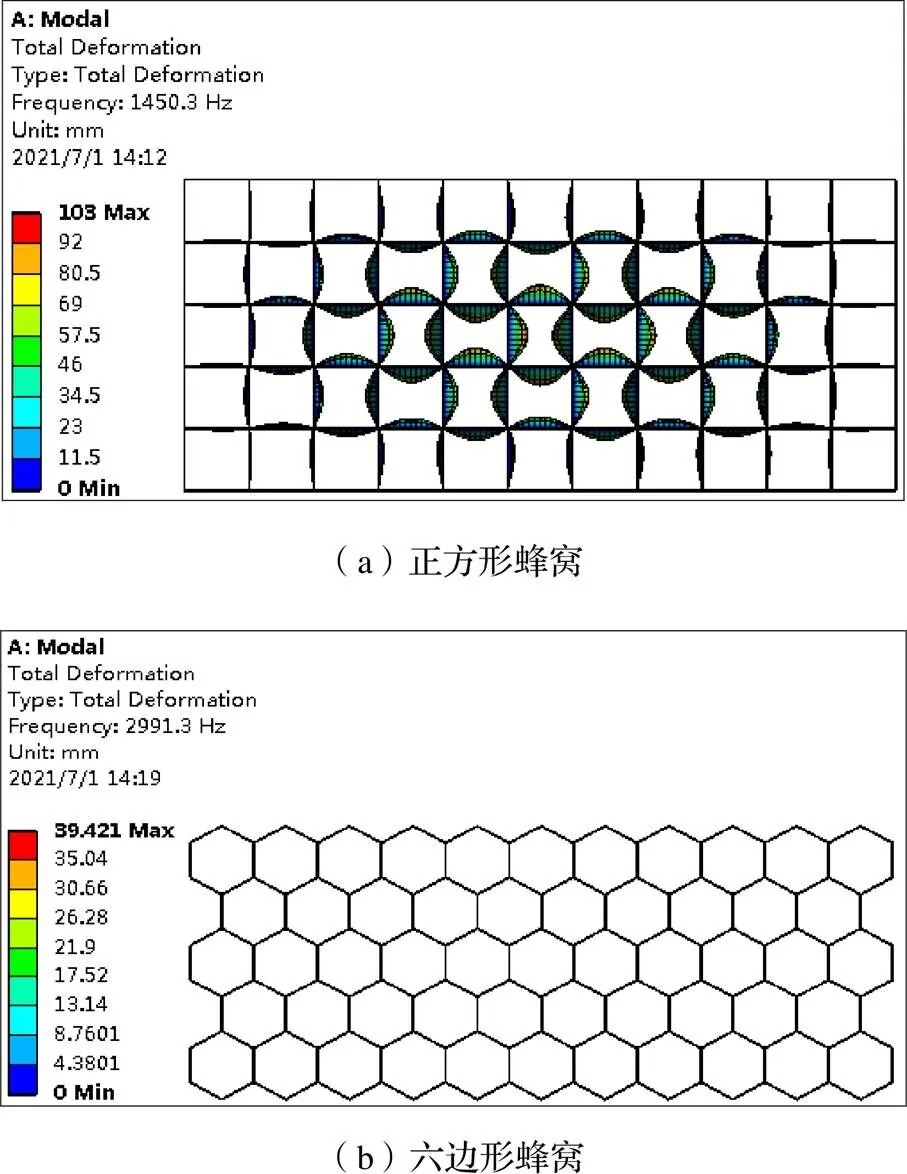
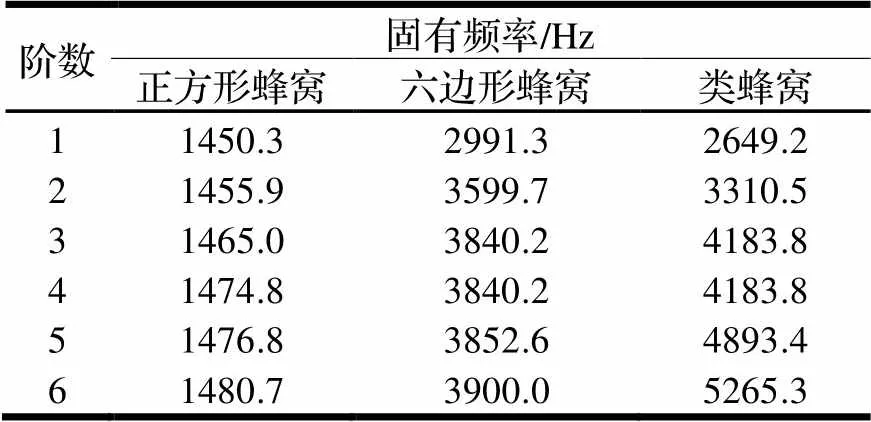
表5 三种夹芯结构前6阶固有频率

根据徐中明[15]研究可知，电动汽车车身的频率为2 Hz左右，轮胎频率为10 Hz左右，汽车悬置系统的振动频率为6～30 Hz。类蜂窝夹芯结构前6阶固有频率远远避开了此类型汽车车身结构的固有频率区间，不会与之产生共振。可满足振动特性要求，并应用在此汽车上。由上述有限元仿真结果可知，从振动固有频率和振动位移上考虑，类蜂窝夹层结构的整体性能更优。

5 结论

以类蜂窝夹层结构为研究对象，对其进行振动特性研究，得到的如下结论：

（1）运用Hoff夹层板理论，计算四边简支边界条件下类蜂窝夹层结构的固有频率，理论计算与有限元模拟结果吻合度较好，振动分析对未来的蜂窝夹层结构设计及应用具有重要意义。

（2）通过有限元仿真计算可知，当类蜂窝夹层结构的蜂窝长度、面板、夹芯等参数数据不变时，增大类蜂窝夹芯壁厚可在整体上提高类蜂窝夹层板振动固有频率，但一阶频率反而有所下降；增大面板与夹层板厚度比，类蜂窝夹层结构的整体的振动频率由于面板与夹层板厚度比的增大而减小，但基频反而缓慢上升。在实际工程应用时可根据具体要求改变结构参数大小进而控制类蜂窝夹层结构的整体频率。由理论及仿真结果可知，影响类蜂窝夹层结构固有频率的主要因素是面板与夹层板厚度比、夹层壁厚、等效剪切模量。

（3）为了进一步验证类蜂窝夹层结构的性能，在相同的条件下，将类蜂窝夹芯与正方形蜂窝夹芯和六边形蜂窝夹芯结构进行仿真模拟对比，根据蜂窝夹芯结构的整体振动固有频率和振动位移等仿真数据可知类蜂窝夹层结构的性能更好。并与某型号电动车车身零件频率对比，得出结论为：类蜂窝夹层结构的整体频率比车身零件频率大可避免共振，可应用于此车底盘甲板中。

[1]Jack R Vinson. The Behavior of Sandwich Structures of Isotropicand Composite Materials[M]. CRC Press：2018.

[2]Zhi-jia Zhang，Qian-cheng Zhang，Fei-chen Li，et al. Modal characteristics of micro-perforated sandwich beams with square honeycomb-corrugation hybrid cores: A mixed experimental- numerical study[J]. Thin-Walled Structures，2019（137）：185-196.

[3]M. Ćetković，Dj. Vuksanović. Bending free vibrations and buckling of laminated composite and sandwich plates using a layerwise displacement model[J]. Composite Structures，2008，88（2）：219-227.

[4]Tat-SengLok，Qian-HuaCheng. Free and forced vibration of simply supported, orthotropic sandwich panel[J]. Computers and Structures，2001，79（3）：301-312.

[5]M. Chandrashekhar，RanjanGanguli. Nonlinear vibration analy-sis of composite laminated and sandwich plates with random material properties[J]. International Journal of Mechanical Sciences，2010，52（7）：874-891.

[6]Reddy J. N. A Simple Higher-Order Theory for Laminated Composite Plates[J]. Journal of Applied Mechanics，1984，51（4）：745-752.

[7]M. E. Raville，C. E. S. Ueng. Determination of natural frequencies of vibration of a sandwich plate[J]. Experimental Mechanics，1967，7（11）：490-493.

[8]中国科学院北京力学研究所固体力学研究室板壳组. 夹层板壳的弯曲稳定和振动[M]. 北京：科学出版社，1977.

[9]卢翔，杨玖月，王瑞鹏，等. 双层蜂窝夹芯结构自由振动特性分析研究[J]. 机械强度，2018，40（5）：1030-1036.

[10]吴晖，俞焕然. 四边简支波形夹层板的振动和稳定[J]. 兰州大学学报，2002（4）：28-32.

[11]李响，李锐，徐兴兴，等. 新型变截面波纹夹层结构抗爆炸冲击性能[J]. 机械，2020，47（10）：6-15.

[12]李响，周幼辉. 超轻多孔类蜂窝夹心结构创新构型及其力学性能[J]. 西安交通大学学报，2014，48（9）：88-94.

[13]张友锋. 弯曲－扭转载荷作用下的类蜂窝夹层结构失效分析[D]. 宜昌：三峡大学，2020.

[14]李响. 承载夹层复合材料的轻量化设计方法及其应用研究[D]. 武汉：武汉理工大学，2011.

[15]徐中明，李晓，刘和平. 纯电动汽车动力总成悬置系统的优化[J]. 汽车工程，2012，34（9）：806-810，815.

Vibration Characteristics Analysis and Application Research of Honeycomb-Like Sandwich Structure

CHEN Yongqing1,2，Qiu Kun2，Li Xiang1,2

(1.Hubei Key Laboratory of Hydroelectric Machinery Design & Maintenance, China Three Gorges University, Yichang 443002, China; 2.College of Mechanical and Power Engineering, China Three Gorges University, Yichang 443002, China )

In this paper, the vibration characteristics of a new honeycomb-like sandwich structure are studied, and the natural frequency equation of the honeycomb-like sandwich structure simply supported with four sides is calculated by using HOFF theory. The vibration modal analysis is carried out with finite element software ABAQUS and the comparison with theoretical value is made. The results show that the error is kept within 10% and the coincidence degree is good, which verifies the feasibility of the theoretical formula. On this basis, the effects of structural parameters, such as wall thickness of honeycomb-like sandwich and thickness ratio of panel to sandwich on the natural frequency of honeycomb-like sandwich structure, are studied. Further study is carried out on the superiority of honeycomb-like sandwich structure. The simulation results show that, compared with hexagonal and square honeycomb-like sandwich structure, with the same number of cells, materials, boundary constraints and other related parameters of honeycomb-like sandwich structure, the performance of the honeycomb-like sandwich structure is better, regarding the natural vibration frequency and vibration displacement. Compared with the frequency of the body parts of a certain type of electric vehicle, the simulation data shows that the honeycomb-like sandwich structure can be used in the chassis deck of the vehicle. Vibration analysis is of great significance to the design of honeycomb sandwich structures in the future, which expands the application of honeycomb structures in engineering.

honeycomb-like sandwich structure；natural frequency；sandwich wall thickness；the modal analysis

TB333

A

10.3969/j.issn.1006-0316.2022.01.002

1006-0316 (2022) 01-0009-08

2021－07－02

国家自然科学基金青年科学基金（51305232）

陈永清（1965－），男，湖北麻城人，高级工程师、副教授，主要研究方向为工程施工特种、工程机械的设计，水电施工专业设备的设计，E-mail：cyq@ctgu.edu.cn。