某型号汽车波纹管液压胀形工艺参数优化研究

刘蕾，周金朝，郭远东，刘超，李萍

某型号汽车波纹管液压胀形工艺参数优化研究

刘蕾，周金朝，郭远东，刘超，李萍

（合肥工业大学 材料科学与工程学院，合肥 230009）

探究波纹管液压胀形成形技术及液压成形过程，优化波纹管成形效果和减薄率。基于正交试验方案，利用有限元技术对成形过程进行数值模拟分析，研究成形内压、轴向进给路径以及保压力对成形效果和减薄率的影响。综合考虑成形高度、减薄率2个指标，得到的较优工艺参数为成形内压为2 MPa，保压力为1.25 MPa，轴向进给路径为在前0.1 s进给5 mm、后0.9 s匀速进给至模具闭合，此时成形高度为12.01 mm，减薄率为9.9%。通过正交试验设计分析，轴向进给路径既是成形高度的显著性影响因素，又是减薄率的显著性影响因素；同时，单独优化一个指标（成形高度、减薄率）时，另一个指标性能会下降，根据正交试验优化结果选取最优参数组合进行模拟验证，得到的试验结果其综合成形质量较高。

液压成形；正交试验；波纹管；有限元分析

金属波纹管是一种具有波纹结构的圆柱形薄壁结构，在轴向、径向等方向变形的情况下具有很高的柔性，此外，它还具有优良的膨胀吸收和机械运动补偿性能。因此，金属波纹管常用于柔性连接元件，在汽车、航空航天和核工业中得到了广泛的应用，并逐渐向高压、大直径、多层方向发展[1-4]。

在目前的金属波纹管生产技术中，常用工艺有轧制、液压成形等[5-7]，许多学者对这些不同工艺方法成形过程中的应力-应变状态进行了研究[8-10]。其中，液压成形是利用油或水等液体介质在管坯内部施加一定程度的压力，同时在管坯的一个或者两个端部利用特定形状的模片进行轴向进给，使管坯在径向产生所需塑性变形的一种成形工艺。影响波纹管液压成形质量的工艺参数涉及多个方面，如模片的轴向进给位移、液体介质的成形内压、管坯自身尺寸等，这些影响因素控制不当，易在液压成形过程中产生起皱、壁厚不均、破裂等缺陷。

Li等[10]和李慧芳等[11]对多层多波Ω形波纹管的液压成形过程进行了仿真，主要分析了成形后的应力和应变场、峰值处壁厚减薄率和各层圆度。李凯[12]对小直径薄壁U型波纹管内压成形过程进行了模拟，获得了应力-应变以及壁厚减薄率的分布演变规律。郭煜敬等[13]则主要通过模拟分析了轴向加载路径和成形内压对薄壁波纹管壁厚减薄率的影响行为。这些研究都是针对特定的金属波纹管的成形过程进行分析，因此为了获得高质量的产品，研究所需波纹管的成形特性并探索合适的成形参数是至关重要的。

文中需要使用304不锈钢管坯成形出具有特定形状的波纹管，其形状是在U形波纹顶部具有直径更小的另一个U形波纹，如图1所示，这对成形内压以及轴向进给的调控要求比普通U形管更高。

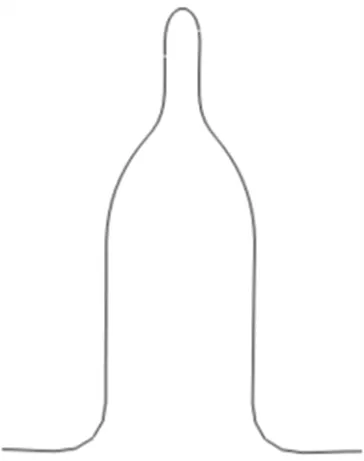
图1 波纹管的几何形状

对中型单层单波不锈钢波纹管进行液压成形数值模拟，并利用数值模拟结合正交分析的方法优化了其工艺参数，避免了工艺参数控制不当导致的褶皱、破裂等成形问题。以成形波高和减薄率为指标，以成形内压、轴向进给路径、保压力为优化因素，实现了工艺参数优化，对该类型波纹管的精确成形提供了参考。

1 有限元模型的建立

波纹管管坯材料为SUS304不锈钢，直径为108.2 mm，波高为12.2 mm，波谷处圆角半径为1.1 mm，厚度为0.2 mm。基于ABAQUS软件有限元模拟平台，建立304不锈钢波纹管液压胀形全过程的三维有限元简化模型。304不锈钢密度为7900 kg/m3，弹性模量为200 GPa，泊松比为0.3，屈服强度为250 MPa，抗拉强度为520 MPa。

文中所成形的波纹管在成形过程中，每一个波形的应力-应变状态较为相似，因此为提高计算效率，只选择其中1个波形进行成形分析。又因为波纹管的结构为轴对称，这里采用1/4个模型进行成形。在所采用的1/4模型中心的横、纵向截面上施加对称约束，使其不会产生位移和转矩。文中采用均匀作用于管坯内表面的施压方式，整个成形阶段模拟时间为1 s。固定右端模片，左边模片采用位移方式沿轴线方向进行运动约束，其位移为20.8 mm；密封圈与管坯端面设置绑定接触，无相对滑动。

管坯网格使用壳单元S4R，模具网格使用刚性单元R3D4。胀形过程采用动态显式算法分析，管坯与模具的接触采用面面接触方式，摩擦采用罚函数法定义，摩擦因数为0.1。波纹管液压胀形有限元模拟模型如图2所示。

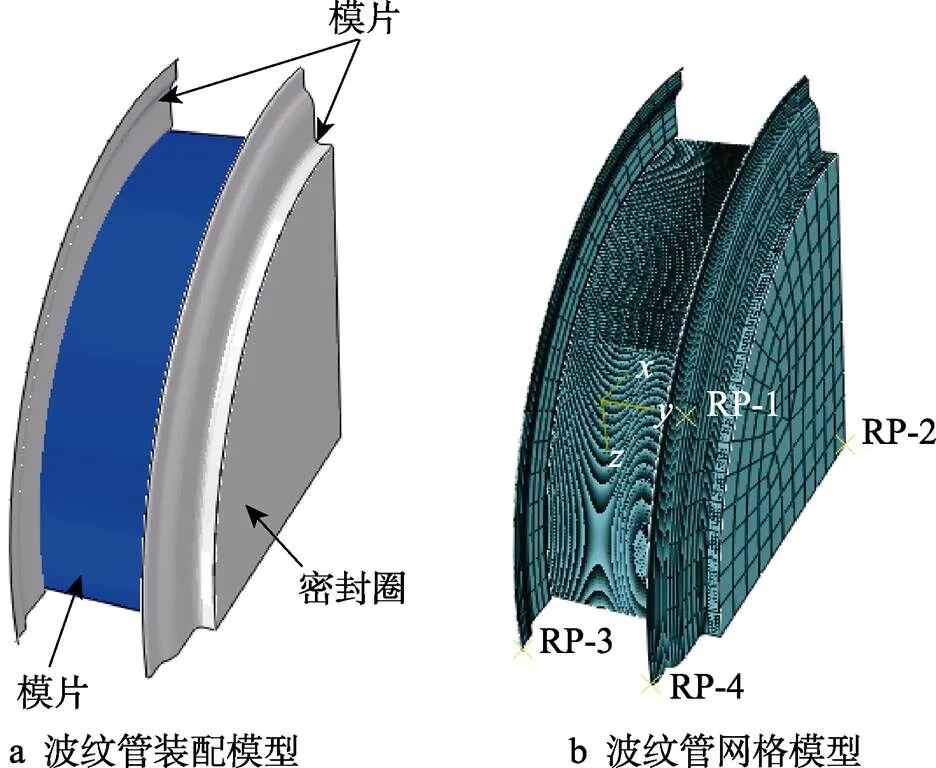
图2 波纹管有限元模型

2 实验设计和结果处理

2.1 波纹管胀形过程应力-应变关系

在假设初始管坯为理想刚塑性材料的前提下，胀形过程中，根据Levy-Mises塑性流动理论，波纹管的应力-应变存在下列关系[14]，即

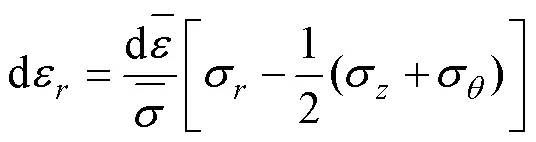
1.2.1.3 健康教育 专责护士每天抽出一定的时间与患者沟通，用通俗易懂的语言讲解相关知识及治疗的配合事项。根据评估内容制定健康教育计划，指导患者纠正不良生活行为，给予日常生活方式指导，如保持正常的坐姿和合理使用枕头等。

根据薄膜理论，文中的管坯壁厚（0.2 mm）远小于半径（108.2 mm），属于薄壁管件，可以忽略径向应力的影响，则式（1）可以简化为：

波纹管在液压胀形过程中，其厚度变化与应力-应变状态有关。由式（2）可以得到：当σ+σ<0时，d>0，主要表现为管坯的厚度增加，此时易发生皱褶等缺陷；当σ+σ>0时，d<0，则厚度减薄，此时则易发生破裂等缺陷；而当σ+σ=0时，d=0，此时厚度保持理想状态一直不变。因此，为了避免各种缺陷，应尽量使管坯处于σ+σ=0的应力状态。

波纹管液压胀形过程中的主要影响因素包括成形内压、轴向进给路径、保压力等。不同的工艺参数和其不同的组合方式可能会导致管坯不同的应力分布状态。需要尽量选择合理的加载路径，避免各种缺陷。

2.2 正交表设计

波纹管液压成形实质上就是管坯在轴向推力和内压力的共同作用下发生的塑性变形，又因为在实际生产中，由于温度、摩擦等客观条件的影响，准确控制轴向推力的大小比较困难，而且使用轴向位移来控制也比较直观，因此使用成形内压A、轴向进给路径B、保压力C作为影响因素来设计因素-水平正交试验。

管材开始发生塑性变形所需要的初始屈服压力s以及管坯产生破裂失效所需要的最小内压力b可由式（3—4）[15]得出：

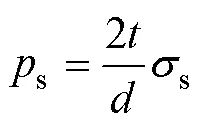
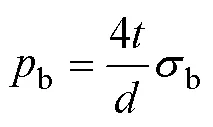
式中：为管材壁厚（mm）；为管材直径（mm）；s为材料屈服强度（MPa）；b为材料抗拉强度（MPa）。

带入304不锈钢的材料屈服强度和抗拉强度，计算得到成形所需内压力为0.924～3.8 MPa。又通过前期模拟可知，当成形内压过小（1 MPa）时，由于内支撑力不够，塌陷缺陷比较明显，如图3a所示；当内压过高（3 MPa）时，金属的塑性变形量就会加大，出现顶出模片的缺陷，如图3b所示，所以折中选择了2，2.25，2.5 MPa的成形内压。而保压力一般只需要>1.2s即可，所以选择1.25，2.5，5 MPa的保压力。

文中的加载路径是指成形内压与轴向进给之间的匹配关系，一般将时间作为中间变量，通过确定和随的变化曲线，从而将二者联系起来。一般对于波纹管液压成形加载路径有台阶形加载路径、双线性加载路径、单线性加载路径以及二次曲线加载路径[17]。文中选择台阶形加载路径、双线性加载路径、单线性加载路径作为正交试验的不同水平。

图3 内压为1 MPa和3 MPa的波纹管成形轮廓

根据因素水平表（见表1）采取L9(33)正交表进行正交试验，正交试验可确定成形过程中的显著性因素[16]，正交试验方案如表2所示。

图4 液压力和轴向进给加载路径的幅值曲线

表1 因素水平表

Tab.1 Factor levels

表2 试验方案

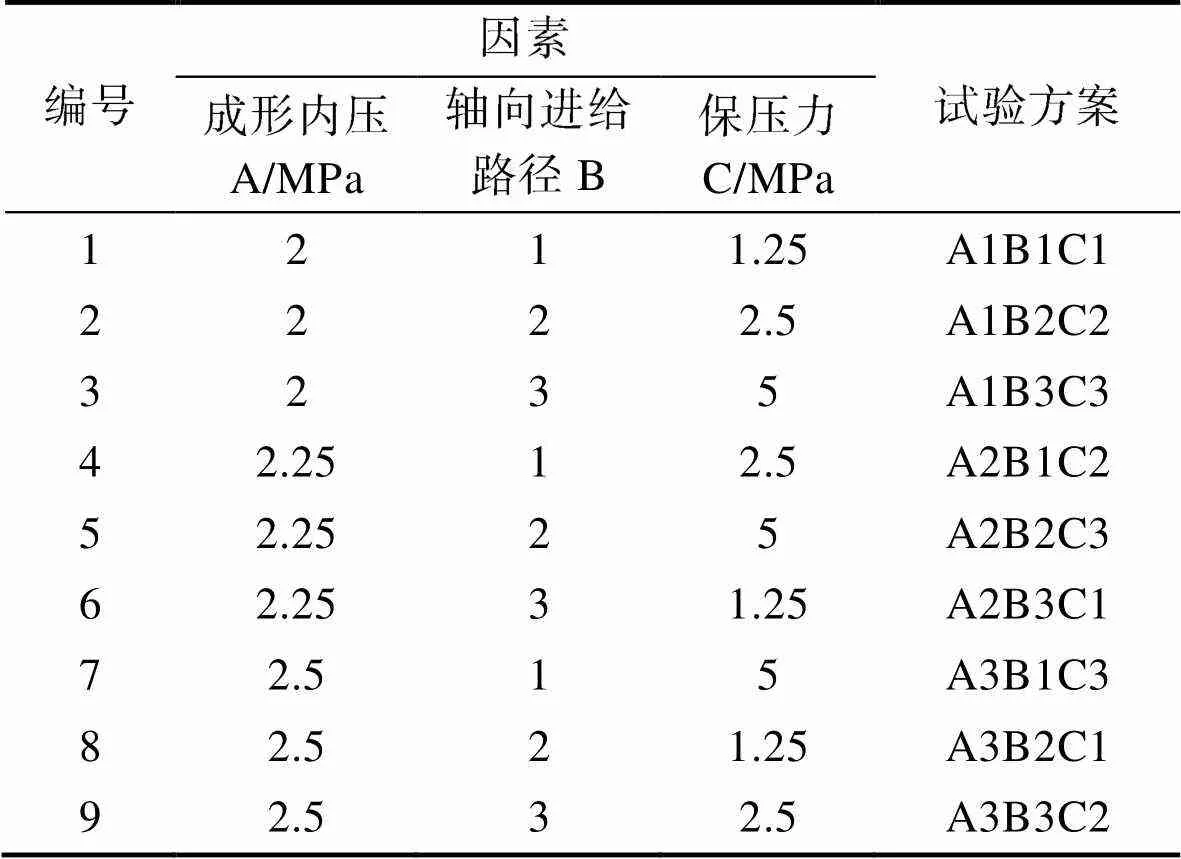
Tab.2 Test plans

2.3 正交试验结果

根据选用的正交试验表进行数值模拟，得出9组成形结果，方案1的模拟结果成形轮廓如图5所示，可以看到管料很好地贴合模片，这证明了加载路径是合理的。但是在2 MPa的内压下，成形出的波峰距直径为120.4 mm的模片顶端有0.3 mm的距离，需要进一步优化。

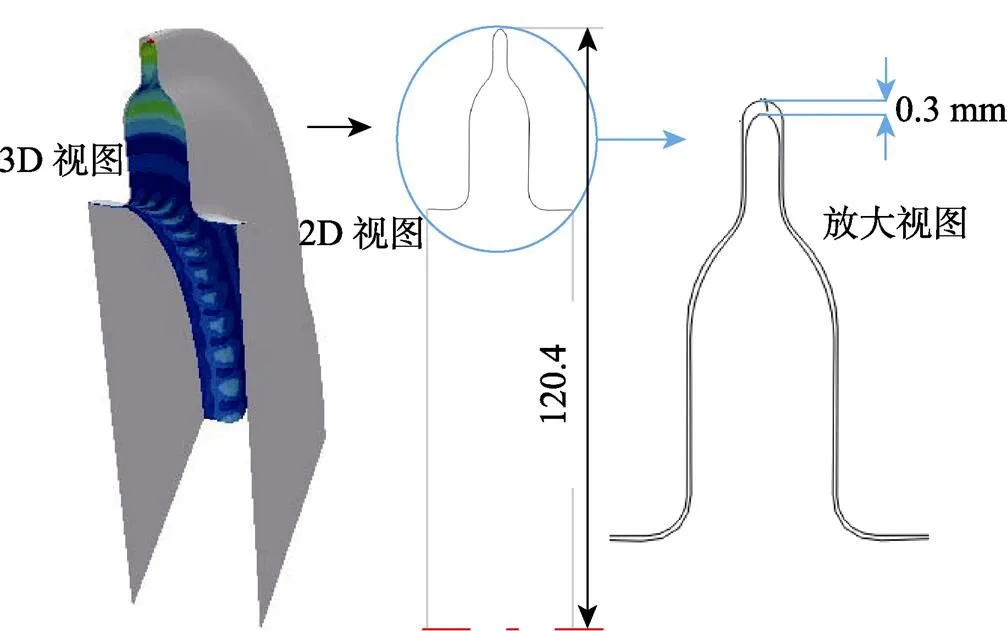
图5 试验方案1的成形轮廓

方案1成形后的等效应力-应变状态见图6。由图6a可以得到，波峰外端区域所受的应力最大，此处成形最困难，成形高度容易达不到要求。从图6b可知，在成形结束时，波纹管不同区域的等效应变值区别明显，应变由大到小的区域分别为波峰外端、波峰、波谷。波峰外端区域的应变最大，是波纹管厚度减薄最严重的区域。

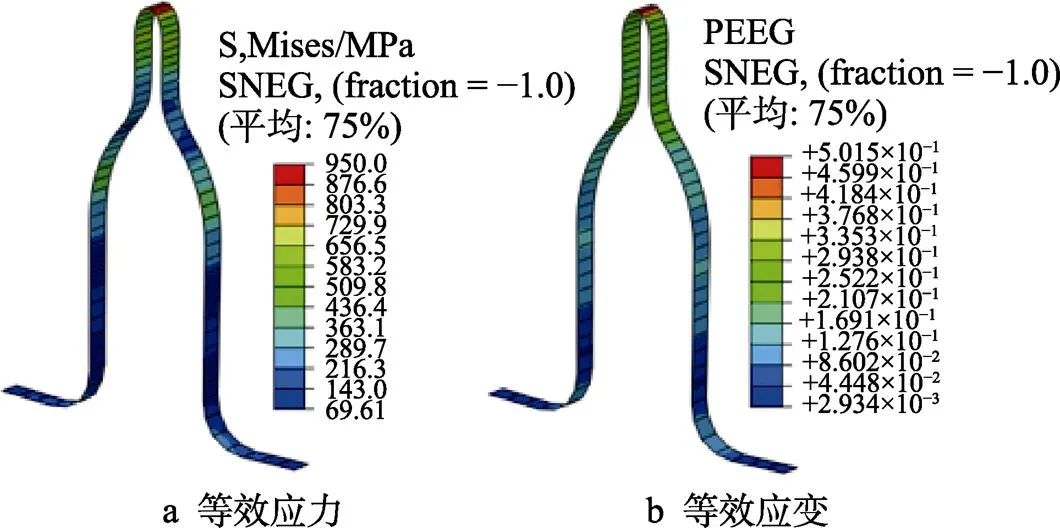
图6 试验方案1的应力应变分布

文中波纹管波形的成形高度需达到12.2 mm，波纹管标准减薄率为15%。同时，9组方案结果如图7所示，可以看到各组成形高度及减薄率区别明显。因此，可以采用波峰外端区域的成形高度和减薄率分别作为正交试验指标，来衡量不同工艺参数下波纹管成形质量。

图7 9组方案的成形高度和减薄率

2.4 结果数据分析

正交试验结果如表3所示。为极差，H表示水平号=1，2，3时分别所对应的试验结果之和。极差数值越大，所对应的因素越重要。因此，对成形高度分析时，三因素影响从大到小分别为：B，A，C。对减薄率分析时，则为B，C，A。由每个因素的H可得到，在成形高度为优选指标时，各个因素下成形高度最高的分别为A3，B1，C3；在减薄率为优选指标时，减薄率最低的为A1，B3，C1。综上可得到，在成形高度为优选指标时，优选组合为B1A3C3；在减薄率为优选指标时，优选组合为B3C1A1。

以成形高度和减薄率作为2个指标，分别对正交试验结果进行分析。由表3可知，在9次试验中，7号方案成形高度最高，为12.18 mm，结合表3可得到其水平组合为A3B1C3；6号方案减薄率最低为9.55%，结合表2可得到其水平组合为A2B3C1。成形结果如图8所示。

表3 正交试验结果

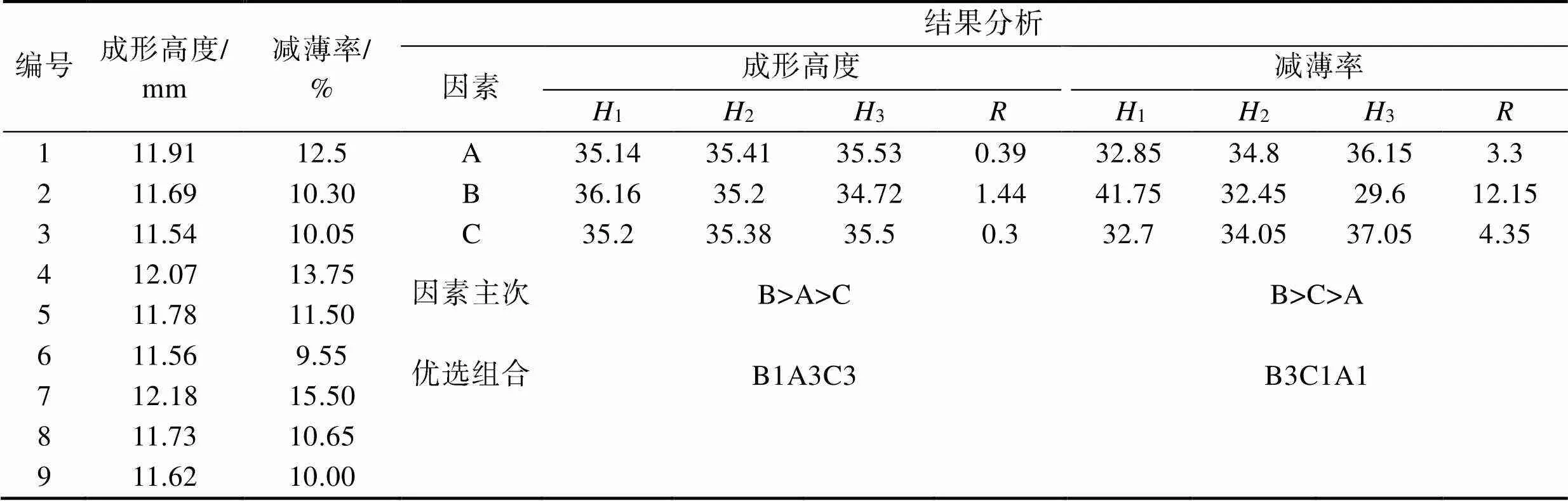
Tab.3 Result of orthogonal experiment

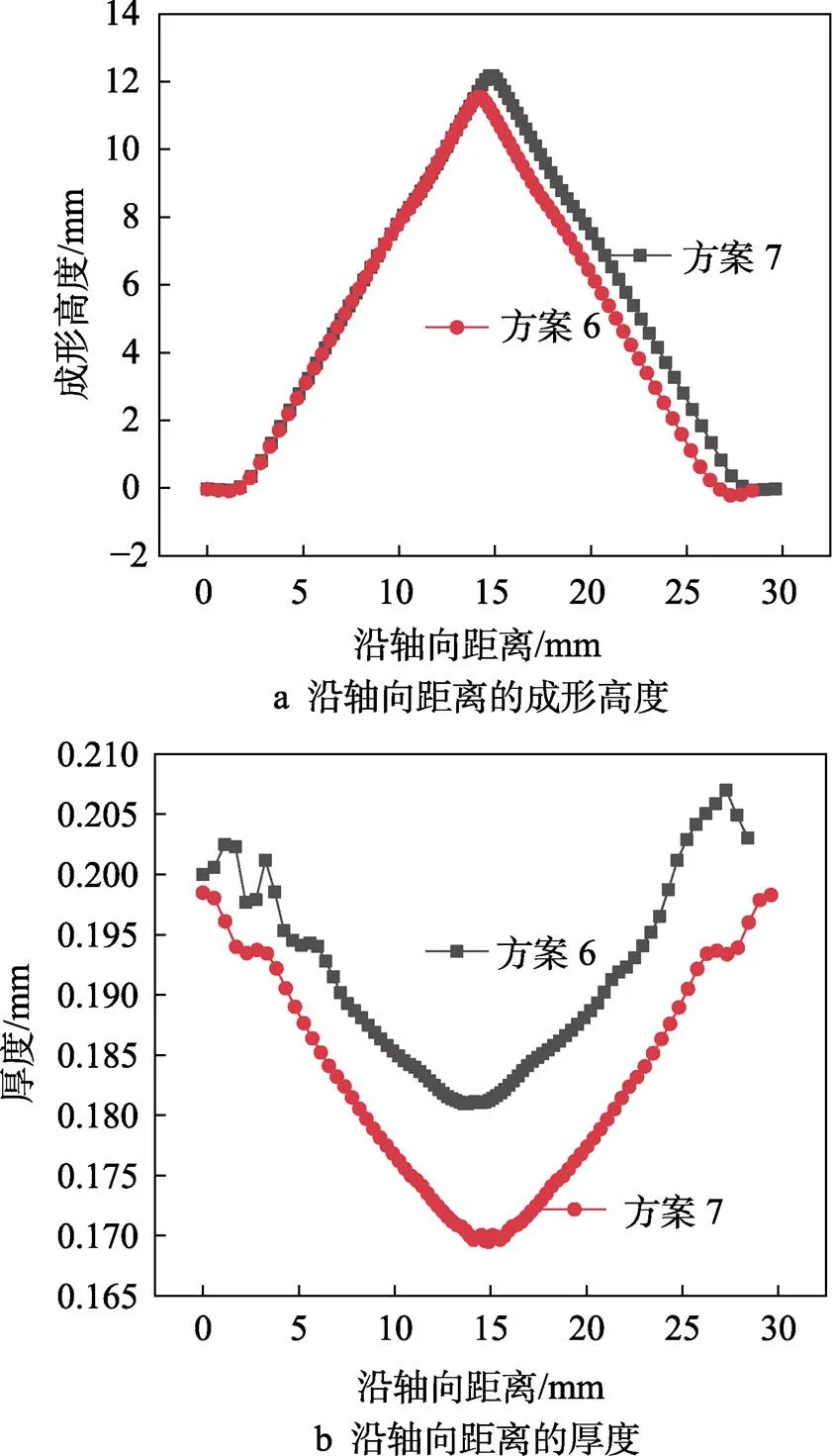
图8 方案6和7的成形高度和厚度

再由表3可得到各因素与成形高度、减薄率的关系曲线，如图9a和b所示。由图9可以直观得到，每个因素对2个指标的影响是相反的，成形高度越高的因素水平，其减薄率越高。

图10和11分别为方案6和7起波、胀形和成形完成时管材的各向应力分布云图。对比图10和11的c及f，可得成形完成时方案7轴向应力值较小、而周向应力值较大，则结合式（2）可知，方案7此时的d更小，说明在板料厚度不变的情况下，成形内压及保压力越大，成形高度越高，其变形量也越大，减薄也越严重。对比图10和11的b及e，结合式（2）可知，方案6胀形时期的（σ＋σ）较小，d接近正值，减薄率会降低。可以得到，在管坯的总轴向进给位移不变的前提下，成形初期坯料进给速度较快（路径3）可以使波纹管的减薄率减小。对比图10和11的a又可得，较快的进给速度下管材会发生褶皱现象，这种现象随着液压力的增大，会逐渐消失。结合表4方案7和6的成形高度，说明在成形初期管坯的轴向进给量越多，最终波纹管的波高越低。

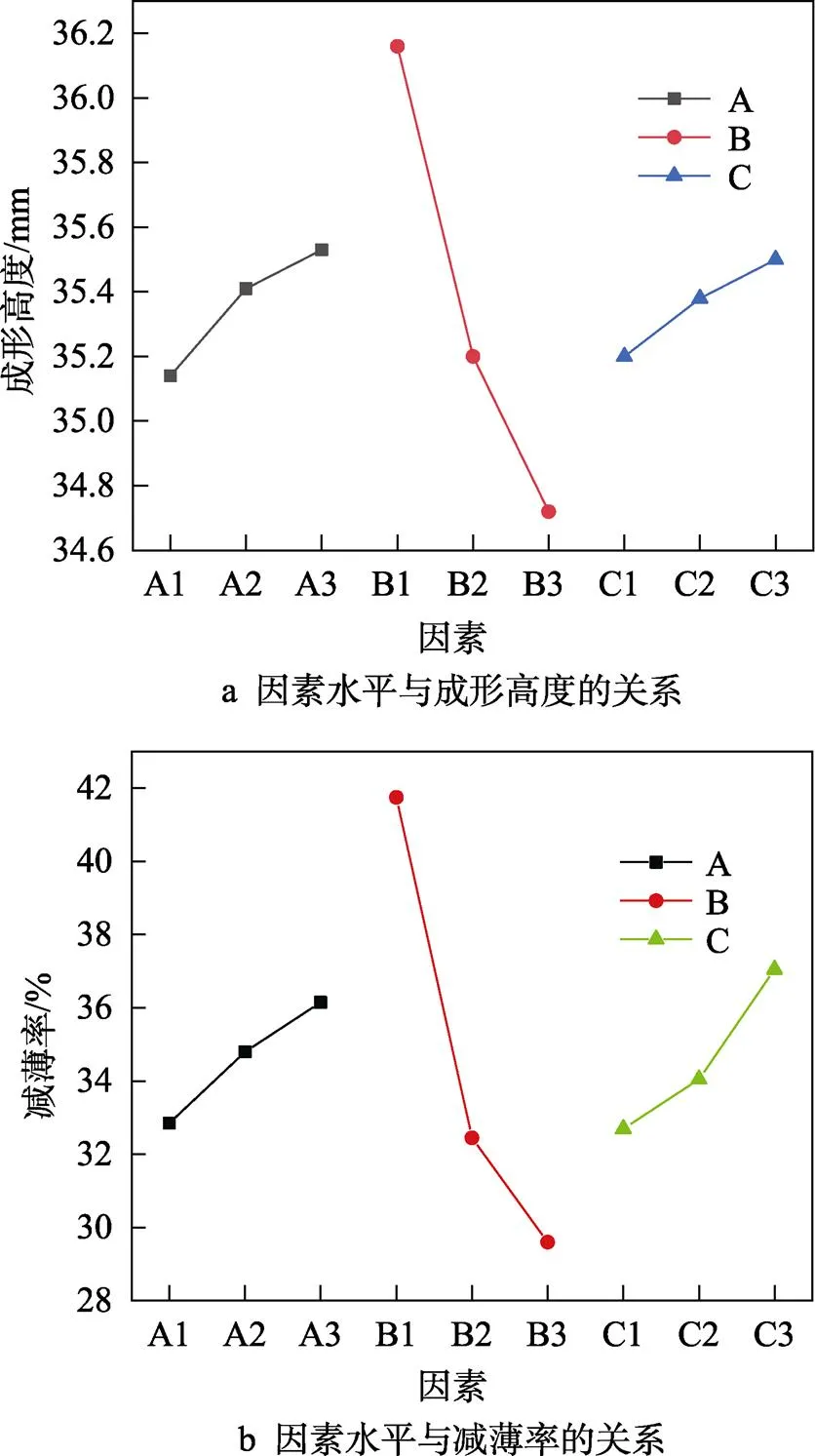
图9 因素-指标图

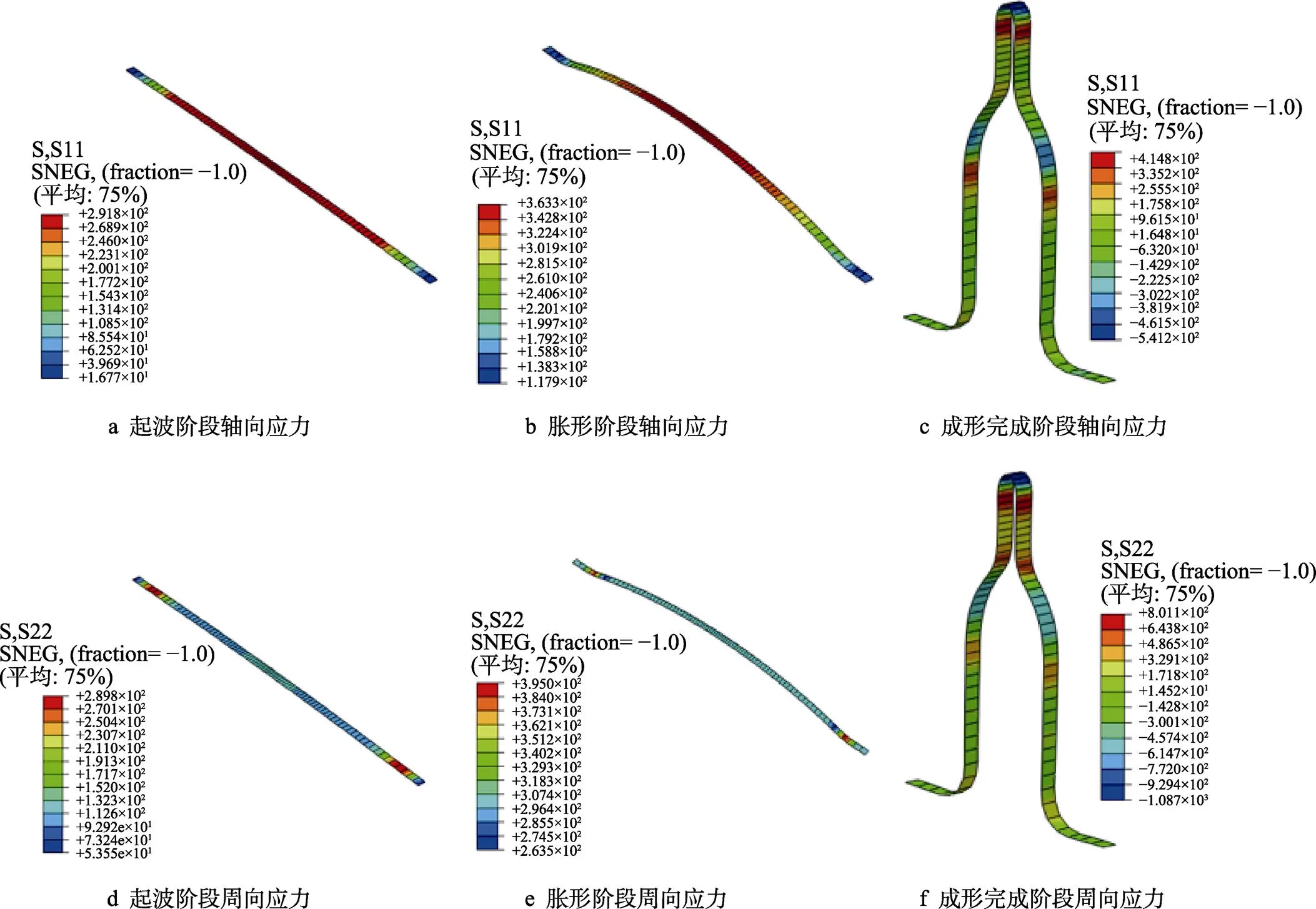
图11 方案7各向应力分布云图(MPa)

2.5 参数优化

对于多种指标的正交试验，可以利用将多种指标转换为一种指标的排队评分法进行数据分析。排队评分法是将各试验所得到的指标值与该指标的优秀值进行评分，各指标的分数相加则为该试验的综合评分。评分数值最高的方案则为最佳方案。文中采用排队评分法分析正交试验数据。对于成形高度指标，将各个试验数据与波纹管波高12.2 mm相减得到相应的评分。对于减薄率指标，将该波纹管的标准减薄率15%减去各个试验数据，得到相应的评分。对每号试验所有指标的分数相加即得综合评分，综合评分结果如表4所示。

表4 排队评分法结果

Tab.4 Result data of queuing scoring method

依据每组试验的评分数值，极差分析如表5所示，其中R为极差，k1，k2k3各自为因素1，2，3水平组合的平均值，K1，K2，K3各自为因素1，2，3水平组合的试验评分数值之和。

表5 排队评分法极差分析

Tab.5 Range analysis of queuing scoring method

由表4可知，6号（A2B3C1）试验评分数值最高为4.81，其成形高度和减薄率的试验结果分别为11.56 mm和9.55%。根据极差分析表，因素主次顺序为BCA，最佳方案是B3C1A1。该方案不在已做过的9组试验中，必须追加一组模拟方案10。方案10所得成形高度和减薄率的试验结果分别为12.01 mm和9.9%，经过评分得到分数为4.91明显优于6号，所以得到优化方案10。

3 结论

1）根据正交试验，确定了成形参数影响显著性排序及影响规律。轴向进给路径是模拟结果中对成形高度和减薄率最主要的影响因素。其他因素里，成形内压及保压力越大，成形高度越高，减薄也越严重。成形初期快速进给有利于减小波纹管的减薄率，但是同时成形初期会出现褶皱，最终波纹管波高比较低。

2）通过正交试验后的数据分析，确定了模拟实验范围内的最佳成形工艺参数。通过综合评分法中的排队评分法，对成形高度和减薄率2个指标综合衡量，得到的优化参数为成形内压为2 MPa，保压力为1.25 MPa，轴向进给路径在前0.1 s进给5 mm、后0.9 s匀速进给至模具闭合。此时综合成形质量较高。

[1] FARAJI G, MASHHADI M, NOROUZIFARD V. Evaluation of Effective Parameters in Metal Bellows Forming Process[J]. Journal of Materials Processing Technology, 2008, 209(7): 3431-3437.

[2] ZHE Yuan, HUO Shi-hui, REN Jian-ting. Mathematical Description and Mechanical Characteristics of Reinforced S-Shaped Bellows[J]. International Journal of Pressure Vessels and Piping, 2019, 175: 103921-103931.

[3] KUMAR J, KUMAR S, JEYATHILAK R K, et al. Effect of Design Parameters on the Static Mechanical Behaviour of Metal Bellows Using Design of Experiment and Finite Element Analysis [J]. International Journal on Interactive Design and Manufacturing (IJIDeM), 2017, 11(3): 535-545.

[4] 詹梅, 石丰, 邓强, 等. 铝合金波纹管无芯模缩径旋压成形机理与规律[J]. 塑性工程学报, 2014, 21(2): 108-115.

ZHAN Mei, SHI Feng, DENG Qiang, et al. Forming Mechanism and Rules of Mandreless Neck-Spinning on Corrugated Pipes[J]. Journal of Plasticity Engineering, 2014, 21(2): 108-115.

[5] HU Sheng-han, EL-ATY A ABD, CHENG Cheng, et al. The Influence of the MRE Forming Medium and Axial Feeding on the Forming Quality of Thin-Walled Inconel 718 Bellow Manufactured by a Bulging Process: Finite Element Simulation and Experimentation[J]. The International Journal of Advanced Manufacturing Technology, 2021, 112(1/2): 387-400.

[6] LEE S. Study on the Forming Parameters of the Metal Bellows[J]. Journal of Materials Processing Technology, 2002, 130: 47-53.

[7] 丁子祈, 何乃辉, 韩先洪. 金属波纹管热屈曲成形数值模拟研究[J]. 塑性工程学报, 2020, 27(11): 109-114.

DING Zi-qi, HE Nai-hui, HAN Xian-hong. Numerical Simulation Study on Thermal Buckling Forming of Metal Bellows[J]. Journal of Plasticity Engineering, 2020, 27(11): 109-114.

[8] BECHT C. Fatigue of Bellows, a New Design Approach[J]. International Journal of Pressure Vessels and Piping, 2000, 77(13): 843-850.

[9] BELAEV A, ZINOVIEVA T, SMIRNOV K. Theoretical and Experimental Studies of the Stress-Strain State of Expansion Bellows as Elastic Shells[J]. St. Petersburg Polytechnical University Journal: Physics and Mathematics, 2017, 3(1): 7-14.

[10] LI Jin-nan, YU Hong-jie, QIAN Cai-fu, et al. Hydroforming Simulation and Analysis of Ω-Shape Expansion Joint[J]. IOP Conference Series: Materials Science and Engineering, 2019, 504(1): 012049.

[11] 李慧芳, 叶梦思, 钱才富, 等. 多层多波Ω形波纹管液压成形的数值模拟[J]. 压力容器, 2018, 35(6): 70-77.

LI Hui-fang, YE Meng-si, QIAN Cai-fu, et al. Numerical Simulation of Hydraulic Forming of a Multi-Layered and Multi-Corrugated Ω-Shape Bellows[J]. Pressure Vessel Technology, 2018, 35(6): 70-77.

[12] 李凯, 苗晓军, 皇涛, 等. 内压对小直径薄壁U型波纹管成形规律的影响[J]. 锻压技术, 2020, 45(10): 66-72.

LI Kai, MIAO Xiao-jun, HUANG Tao, et al. Effect of Internal Pressure on Forming Law of Thin-Wall U-Shaped Bellows With Small Diameter[J]. Forging & Stamping Technology, 2020, 45(10): 66-72.

[13] 郭煜敬, 王志刚, 金光耀, 等. 液压成形波纹管减薄率的数值模拟研究[J]. 浙江工业大学学报, 2019, 47(1): 58-62.

GUO Yu-jing, WANG Zhi-gang, JIN Guang-yao, et al. Numerical Simulation Research on Thickness Reduction Ratio of the Bellows[J]. Journal of Zhejiang University of Technology, 2019, 47(1): 58-62.

[14] 夏彬. 中小直径波纹管内压成形技术的研究[D]. 哈尔滨: 哈尔滨工业大学, 2011: 13-14.

XIA Bin. Research on the Hydroforming Technology of Small Diameter Bellows[D]. Harbin: Harbin Institute of Technology, 2011: 13-14.

[15] 唐治东. 波纹管液压成形过程的数值模拟与实验研究[D]. 杭州: 浙江工业大学, 2015: 23-24.

TANG Zhi-dong. Numerical Simulation and Experimental Study of Bellows Hydroforming[D]. Hangzhou: Zhejiang University of Technology, 2015: 23-24.

[16] 崔磊. 基于响应面法的双层波纹管液压胀形工艺参数优化[D]. 西安: 西安石油大学, 2019: 14-15.

CUI Lei. Optimization of Hydroforming Process Parameters of Bi-layered Bellows Based on Response Surface Method[D]. Xi'an: Xi'an Shiyou University, 2019: 14-15.

Optimization of Hydraulic Bulging Process Parameters of a Certain Type of Automobile Bellows

LIU Lei, ZHOU Jin-zhao, GUO Yuan-dong, LIU Chao, LI Ping

(School of Materials Science and Engineering, Hefei University of Technology, Hefei 230009, China)

The work aims to investigate the hydraulic expansion forming technology and hydraulic forming process of bellows, so as to optimize the forming effect and thinning rate of bellows. The effects of forming internal pressure, axial feed path and holding pressure on forming quality and thinning rate were studied by numerical simulation of the forming process with finite element technology based on an orthogonal test plan. Taking into account the two indicators of forming height and thinning rate, the optimum process parameters were obtained with an internal forming pressure of 2 MPa, a holding pressure of 1.25 MPa, an axial feed path of 5 mm in the first 0.1 s and a uniform feed in the second 0.9 s until the mould closed, at which time the forming height was 12.01 mm and the thinning rate was 9.9%. The orthogonal test design analysis shows that the axial feed path is a significant influence factor on both the forming height and the thinning rate; at the same time, when optimizing one index (forming height, thinning rate) alone, the performance of the other index decreases. The optimal combination of parameters is selected for simulation verification based on the orthogonal test optimization results, and the test results obtained are of high comprehensive forming quality.

hydroforming; orthogonal test; bellows; finite element analysis

10.3969/j.issn.1674-6457.2022.02.003

TG376

A

1674-6457(2022)02-0014-08

2021-07-05

长丰县-合肥工业大学创新引导资金重点项目（JZ2020YDZJ0121）

刘蕾（1996—），女，硕士生，主要研究方向为精密塑性成形工艺与仿真。

李萍（1973—），女，博士，教授，主要研究方向为精密塑性成形工艺与仿真。