分段导轨式动态无线充电系统电压波动性研究
李卫龙,李云俊,时运通,夏晨阳
(1.安徽省煤炭科学研究院,安徽 合肥 230001;2.中国矿业大学,江苏 徐州 221116)
随着全球环境和能源问题的日渐凸显,发展电动汽车显得颇为重要。然而传统电动汽车有线插拔式充电方式存在使用不方便、存在积尘、接触损耗和触电等安全隐患。
电动汽车无线充电技术成为目前研究的热点,其作为无线电能传输(wireless power transfer,WPT)技术的一种,基于感应耦合电能传输(inductively coupled power transfer,ICPT)技术的电动汽车无线充电系统具有传输功率水平较高,能实现中距离无线传输等特点[1-4],可以很好地适应电动汽车静态无线和动态无线充电应用场景[5],因此得到了广泛的关注和研究。
动态无线电能传输技术的产生可弥补静态无线电动汽车充电时间久、续航能力差等问题[6],可实现电动汽车在行驶过程中边走边充,有效地减少电池存储装置自身的重量,减轻电动汽车充电时间长和续航差等问题。
动态无线电能传输根据原边发射线圈的结构可分为线圈阵列式、分段导轨式、长导轨式[7],国内外对于分段导轨式动态无线电能传输的研究最多。对于如何减少电动汽车在行驶过程中系统电压输出波动这一问题,国内外研究学者进行了深入研究,并提出了一系列的方法,主要集中于控制环节的加入[8]、拓扑补偿的设计[9-10]、磁耦合机构的设计[11-12]3个方面,以及三者的结合使用[13-14]。
韩国KAIST研究团队主要研究导轨式动态无线电能传输,自2009年至今先后提出六代电动汽车动态无线电能传输系统[15]。从第四代起该研究团队采用双极性发射线圈配合DD型拾取线圈,降低了磁耦合机构的绕线成本;但动态无线充电过程中互感波动导致的功率波动问题均未得到解决。文献[16]采用阵列式原边发射线圈,优化磁耦合机构尺寸,以减小副边接收线圈在移动过程中的互感波动,该方式的成本较高,逆变器的控制也较为复杂。文献[17]提出了渗透型分段导轨结构,在线圈连接处增加补偿线圈,以减小动态充电过程中的电压波动。文献[18]提出原边采用三相导轨线圈,副边采用DD型线圈的动态无线充电系统,利用三相交流的相位差来减小动态充电过程中的电压波动问题,但与此同时带来了磁耦合机构成本高和系统效率低的问题。文献[19]设计I型双极性原边发射线圈配合多个副边接收线圈使用,从而避免双极性发射线圈的互感过零问题和互感波动问题。文献[20-21]中对原边发射线圈磁耦合机构进行建模,使副边感应到的电压波动更小,但在原边存在能量浪费和设计复杂等问题。文献[22]通过控制原副边电流,让系统有较高效率和更小的电流波动,但需要实时监测互感进行,系统控制比较复杂。
本文对恒压输出补偿LCCL-S双接收拓扑电路在分段导轨式动态无线充电系统中的2种传能状态分别进行建模分析,得出系统的传输特性。后对磁耦合机构进行优化分析,先以取得互感最大值为优化目标得出副边磁耦合机构的最优尺寸比,再基于最优尺寸以降低互感波动为优化目标得出最优的副边磁耦合机构尺寸,使磁耦合机构在单位用线量下获得最大互感值的同时减小磁耦合机构移动过程中互感的波动率。最后,搭建200 W的实验平台验证本文对双接收电路简化理论的正确性和磁耦合机构优化方案的正确性。
1 分段导轨式动态无线充电系统结构与原理分析
1.1 分段导轨式动态无线充电系统原理
电动汽车分段导轨式动态无线充电系统的基本组成结构如图1所示。系统包括2部分,分别是原边发射装置和副边接收装置:原边发射装置由多组分段导轨构成,并对每段导轨进行编号,原边电路包括整流环节、逆变环节、原边补偿网络、切换开关和原边发射线圈,通常铺设于道路表面以下,将电能转换为磁场能量;副边接收装置包括副边接收线圈、副边补偿网络、整流环节、储能装置(电池),通常位于汽车底部,将磁场能量转换为电能。
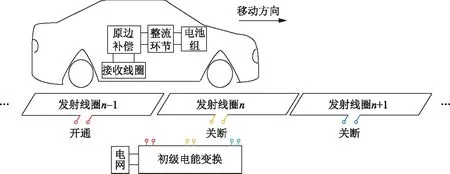
图1 分段导轨式动态无线充电系统
分段导轨式动态无线充电系统的原边发射线圈由多个导轨线圈排列组成,线圈尺寸介于线圈阵列式和长导轨式的原边线圈之间,既可以减少原边线圈的切换频率,又可以有效减少磁泄漏。根据原边发射线圈切换状态,电动汽车分段导轨式动态无线充电系统可分为3个阶段,磁耦合机构的位置关系如图2所示。
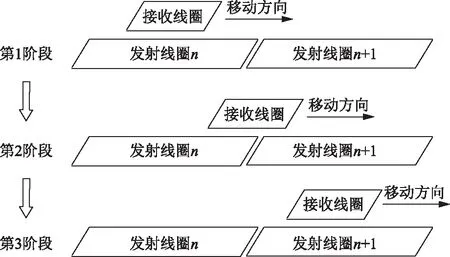
图2 磁耦合机构位置示意图
1.2 分段导轨式动态无线充电系统拓扑
分段导轨式动态无线充电系统中,原边线圈交接处上方磁场变化剧烈,对于采用常规的单极性接收线圈配合单极性发射线圈作为动态无线充电系统的磁耦合机构,其互感在原边线圈交接处附近会存在较大的跌落,开环状态下互感的波动会影响系统电压输出,甚至使系统失谐。
本文采用LCCL-S拓扑补偿双接收电路,电路如图3所示,图中:Udc为直流输入电压,MOS管S1—S4组成高频逆变电路,电感L1、电容C1、电容CP1、电感LP1(相应变量符号为L1、C1、CP1、LP1)和电感L2、电容C2、电容CP2、电感LP2(相应变量符号为L2、C2、CP2、LP2)组成原边LCCL补偿拓扑,电容CS1、电感LS1(相应变量符号为CS1、LS1)和电容CS2、电感LS2(相应变量符号为CS2、LS2)分别组成2个独立的S补偿拓扑,二极管VD1—VD4、VD5—VD8分别组成2个整流电路,电容Cd1、电容Cd2(相应变量符号为Cd1、Cd2)为滤波电容,RL为系统负载(电阻符号为RL)。
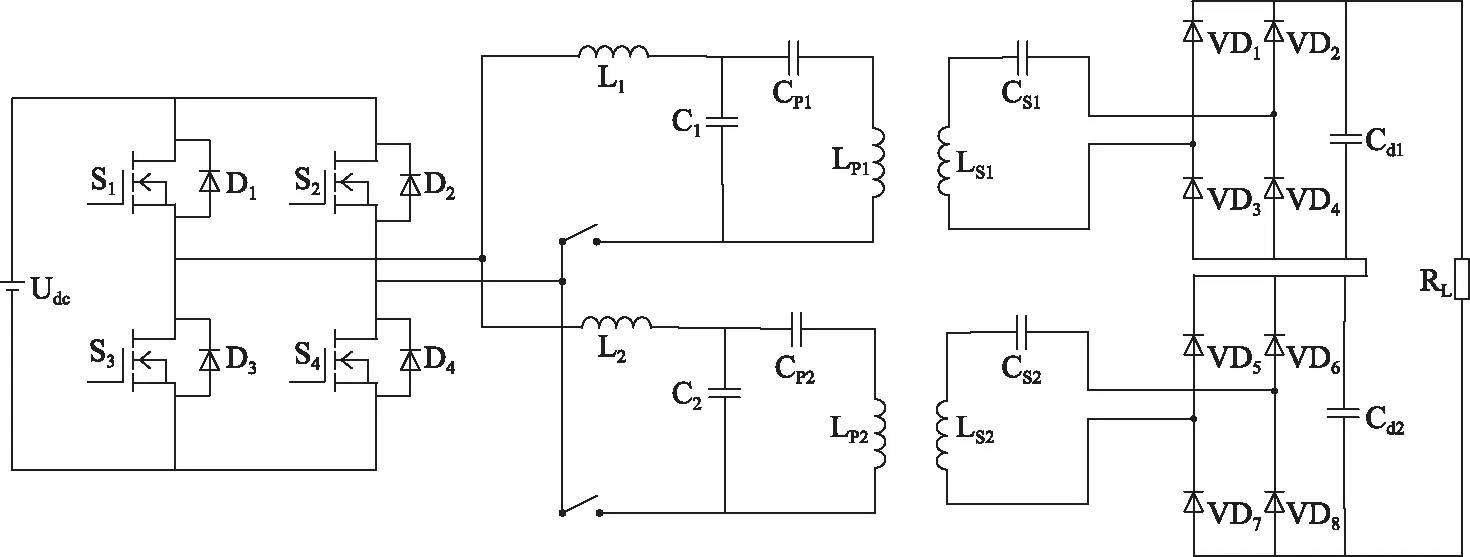
图3 LCCL-S补偿双接收ICPT系统
本文采用双极性发射线圈和双接收副边线圈作为磁耦合机构,副边两接收线圈不直接相连,经过独立的补偿拓扑以及整流环节后再经过串联后输出。本系统可实现磁耦合机构原、副边线圈的互感总和保持恒定,系统的输出电压保持恒定。
1.3 分段导轨式动态无线充电系统磁耦合机构
本文原边的发射线圈采用双极性线圈,两相邻线圈通入的电流相位相差180°,原边发射线圈结构如图4(a)所示,箭头代表某一时刻电流方向。副边接收线圈为一个矩形线圈和一个DD线圈的组合,两线圈之间没有直接相连,其中DD线圈和矩形线圈的大小相等,两者上下叠置,结构如图4(b)所示。副边两线圈处于解耦状态。
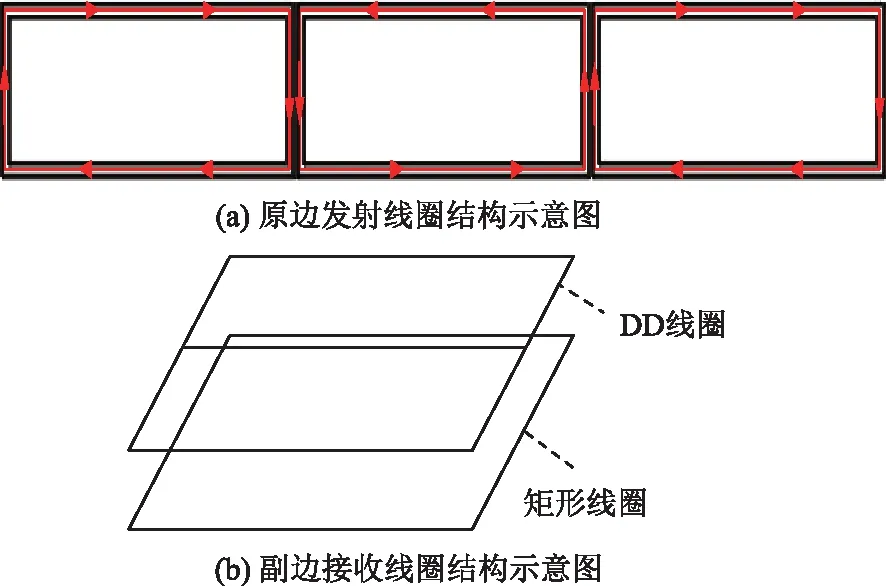
图4 磁耦合机构
当副边线圈在单个原边发射线圈之上移动时,副边矩形线圈与原边线圈互感值相对恒定,当副边线圈移动至原边两发射线圈交接处附近时,副边矩形线圈与原边线圈互感值急剧跌落,此时DD型线圈与原边线圈互感值迅速增加。副边两接收线圈与原边的发射线圈互感之和保持一定的范围,减小了磁耦合机构互感总和的波动。
2 动态无线充电双输出系统建模分析
分段导轨式动态无线充电系统存在2种工作模式:①副边磁耦合机构在仅运行在单根发射导轨之上,此时原边仅有1个发射线圈工作,系统工作在单输入双输出模式;②副边磁耦合机构运行至2根发射导轨连接处,此时原边靠近副边两发射线圈同时工作,系统工作在双输入双输出模式。以下分别对2种状态进行建模分析。
2.1 单输入双输出系统建模
LCCL-S[20]拓扑单输入双输出ICPT系统的等效电路如图5所示,图中:Ui为等效输入交流电压,Rref为副边两电路的反射电阻,US1和US2为副边两接收线圈在原边发射线圈所产生的磁场中的感应电压,RP为发射线圈的等效串联电阻,RS1和RS2为两接收线圈的等效内阻。由于副边两接收线圈处于解耦状态,图中没有表示副边两接收线圈互感电压。
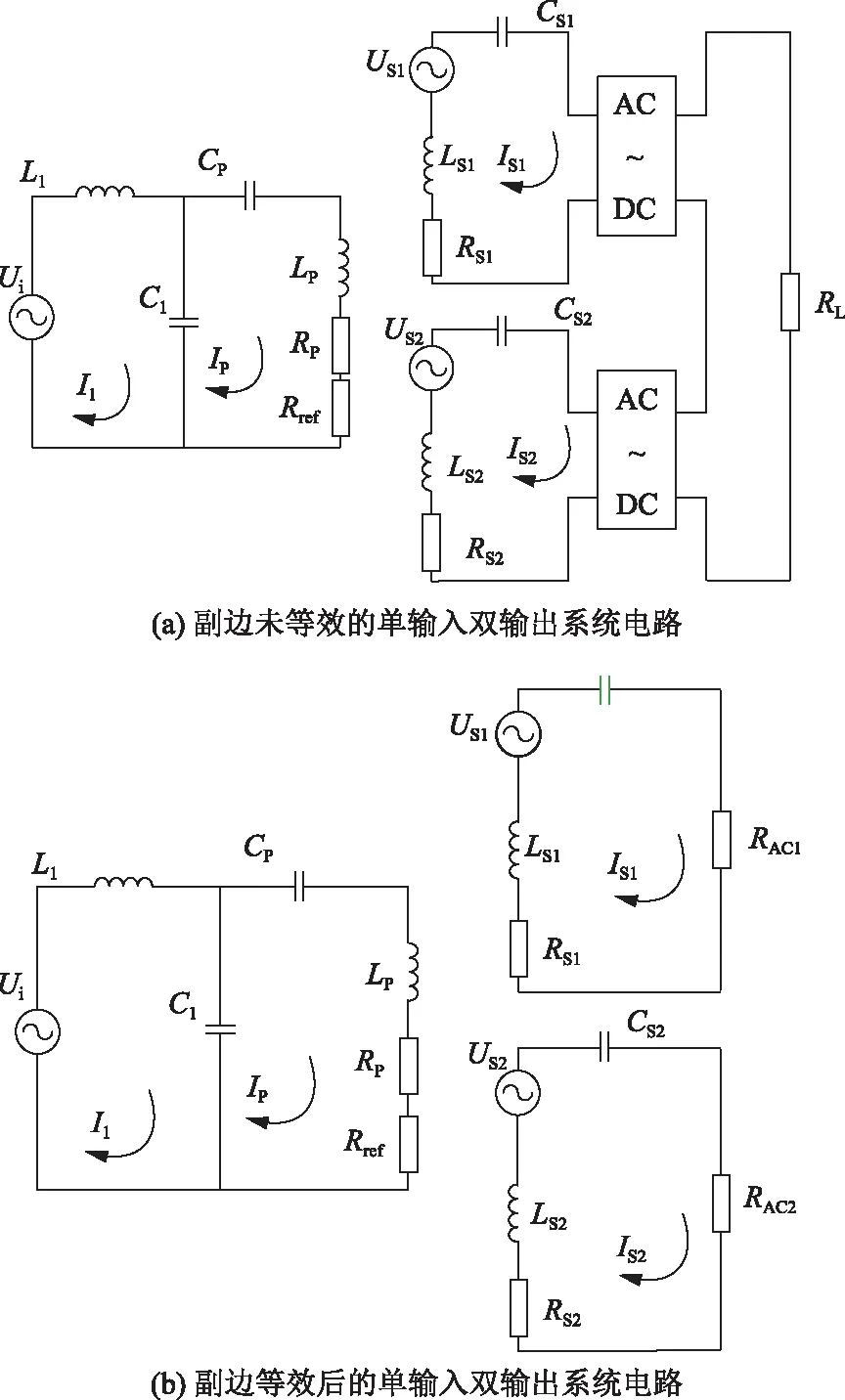
图5 单输入双输出系统电路
记副边两线圈与原边线圈之间的互感分别为M1、M2,原边交流电源所在回路电流为I1,原边发射线圈所在回路电流为IP,副边两接收线圈所在回路电流分别为IS1、IS2,整流环节前的电压分别为Ua1、Ua2,整流环节后的电压分别为Uo1、Uo2,整流环节后的电流分别为Io1、Io2,RL1、RL2,RAC1、RAC2分别为副边两串联电路的直流等效负载及其交流等效负载。
补偿拓扑参数设计关系为:
(1)
式中ω为工频角频率。
基于基尔霍夫电压定律,图5(b)等效电路的数学模型为:
(2)
US1=ωM1IP;
(3)
US2=ωM2IP.
(4)
联立方程式(2)—(4)可得:
(5)
(6)
(7)
(8)
(9)
整流环节前后的等效电压关系为:
(10)
(11)
整流环节前后的等效电阻关系为:
(12)
(13)
记RAC1、RAC2之和为RAC,则
(14)
由副边两接收电路的串联关系,联立式(8)、(9)可得两等效电阻关系如式(15)所示,再结合式(14)可得等效电阻RAC1的表达式如式(16)所示。
(15)
(16)
联立方程(5)—(14)可得图5(a)中负载两端电压
(17)
由式(17)可知,在保证副边两线圈与原边线圈的互感之和M1+M2恒定时,可实现系统输出电压相对恒定。
2.2 双输入双输出系统建模
LCCL-S拓扑双输入双输出ICPT系统的等效电路如图6所示,由于原边发射线圈的电路参数相同,补偿拓扑电路的参数设计也相同 ,另外本文建模分析忽略了原边发射线圈间的互感影响。
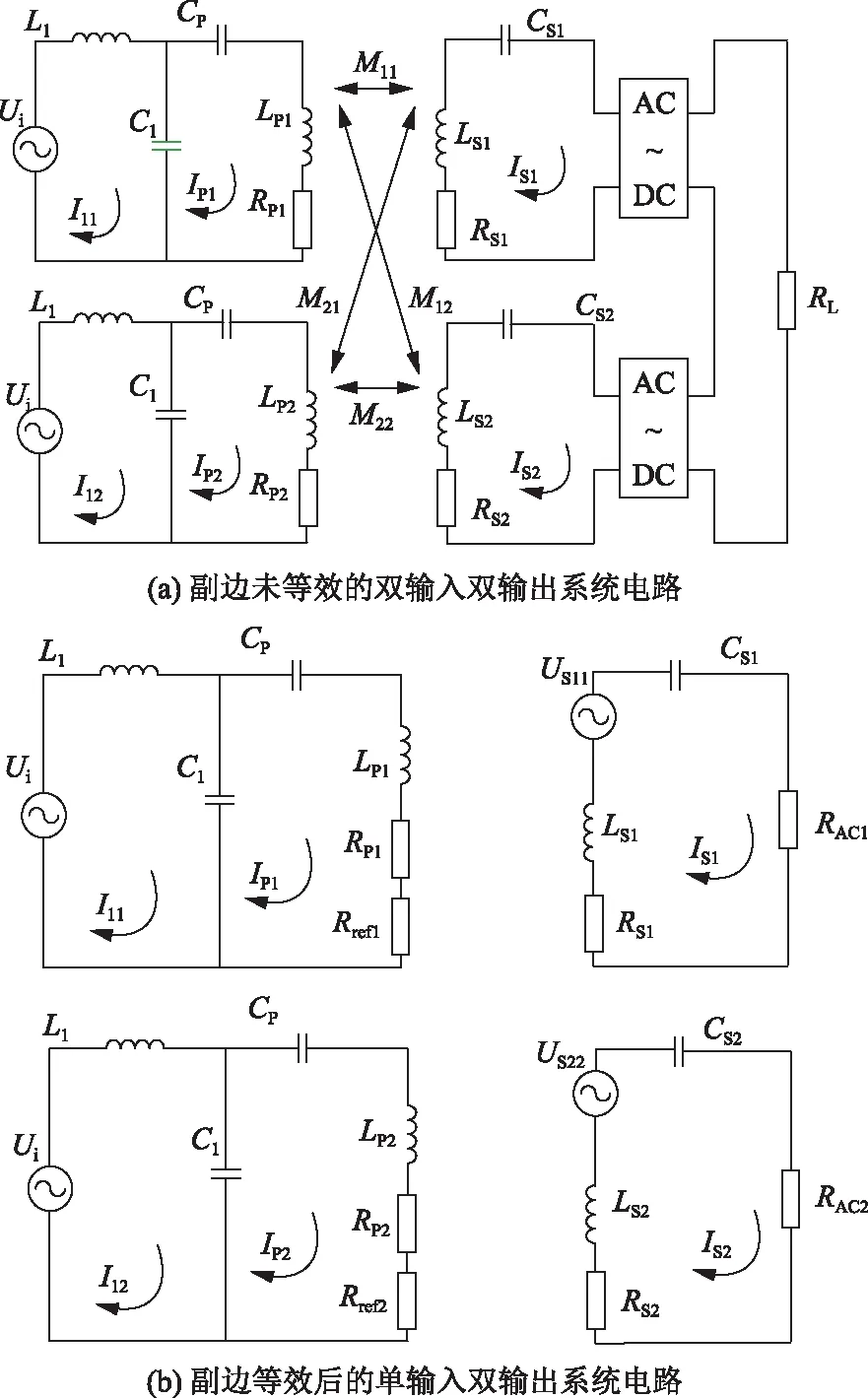
图6 双输入双输出系统电路
记副边两线圈与原边两线圈之间的互感分别为M11、M22、M12、M21,原边两线圈交流电源所在回路电流为I11和I12,原边两发射线圈所在回路电流为IP1和IP2,Rref1为副边两接收电路在原边第1个发射电路上的反射电阻之和,Rref2为副边两接收电路在原边第2个发射电路上的反射电阻之和,US11为副边第1个接收电路在2个原边发射线圈产生的磁场中的感应电压,US22为副边第2个接收电路在2个原边发射线圈产生的磁场中的感应电压。
基于基尔霍夫电压定律,图6(b)等效电路的数学模型为:
(18)
US11=ω(M11IP1+M21IP2).
(19)
US22=ω(M12IP1+M22IP2).
(20)
求解方程组(18)可得原边两发射线圈所在回路的电流相等,如式(21),副边等效交流电阻两端电压分别如式(22)、(23)所示,电流分别如式(24)、(25)所示。
(21)
联立方程(18)—(20)可得:
(22)
(23)
(24)
(25)
副边两接收电路为串联关系,联立式(24)、(25)可得两等效电阻关系如式(26)所示,再结合式(14)可得等效电阻RAC1的表达式如式(27)所示。
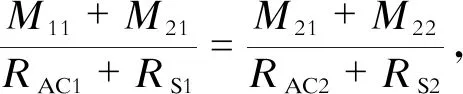
(26)
RAC1=
(27)
联立式(24)、(25)可得图6(a)中负载两端电压
(28)
由式(28)可得,对于双输入双输出系统,保持原副边线圈间的互感和恒定即可实现系统的输出电压相对恒定。综上所述,本文基于LCCL-S补偿的动态ICPT系统保证原边线圈与副边组合线圈的互感总和为定值,即可实现系统输出电压相对恒定。
3 磁耦合机构的设计与优化
本文原边发射线圈为分段导轨式双极性线圈,副边两接收线圈分别为方型线圈和同等尺寸的DD型线圈,磁耦合机构三维坐标系如图7所示,xy平面为地面,副边线圈移动方向为y轴正方向,z轴方向表示原副边线圈之间的距离。另外,与y轴平行的线圈边长称为线圈的长,与x轴平行的线圈边长为线圈的宽。
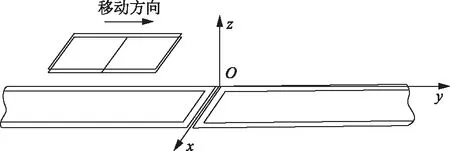
图7 磁耦合机构三维坐标系
3.1 副边磁耦合机构的互感波动分析
图8所示为位于矩形线圈上方h高度平面中平行于y轴的对称轴上Q点坐标示意图。

图8 水平对称轴上方坐标
坐标轴原点建立在矩形线圈的中心位置,矩形线圈的长(线段2、线段4)为2a,矩形线圈的宽(线段1、线段3)为2b。4条导线对点Q所产生的磁感应强度在z轴上的分量BZi(i对应矩形线圈的每个线段编号)为:
(29)
(30)
(31)
(32)
式(29)—(32)中:I为线圈中流过的电流;μ0为真空磁导率。
利用软件绘制矩形线圈中的4条导线在水平对称轴上方h处的磁感应强度分布曲线,如图9所示。分段导轨式原边发射线圈在线圈交接处磁场分布急剧变化,另外,可以看出长边导线所产生的磁感应强度在中间点取极大值,在导线端点附近不存在极值点。矩形线圈中磁感应强度的极大值点主要是受短边导线的影响。
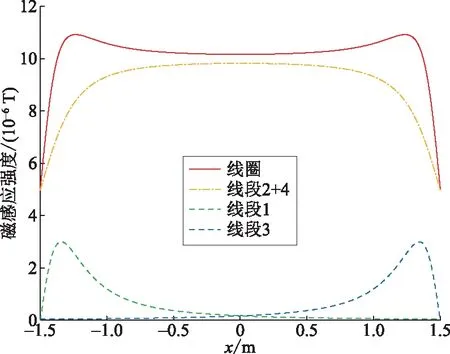
图9 不同导线作用下的磁感应强度分量分布曲线
记导线端点到磁感应强度极大值点的水平距离为Δy。对式(31)求导可得:
(33)
从式(33)中可以看出,Δy与矩形线圈长边导线的长度无关,与位置高度和矩形线圈短边导线长度有关,且受位置高度的影响较大,受矩形线圈短边导线长度的影响较小。
3.2 副边磁耦合机构的尺寸比优化
副边磁耦合机构位置示意图如图10所示,图中:SQ为副边矩形线圈,SDD为副边DD线圈,n为原边线圈编号,h为原副边线圈间的距离。如图10(a)所示,当副边磁耦合机构在单个原边长导轨线圈之上运动时,只有单个原边线圈供电,此时副边方型线圈从原边线圈中汲取电能,DD线圈上感应电压几乎为0。
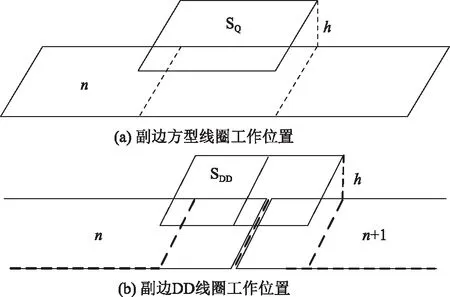
图10 副边磁耦合机构位置
如图10(b)所示,当副边磁耦合机构运动至原边2长导轨式线圈交接处附近时,2个原边长导轨式线圈同时供电,此时副边磁耦合机构中矩形主线圈和DD型辅助线圈共同起作用。当副边磁耦合机构的中心点恰好运动至原边两长导轨式线圈交接处时,DD型辅助线圈从原边线圈中汲取电能。
记副边磁耦合机构的长与宽之比为β、互感取得极大值所对应的长与宽之比为βM。通过固定副边单匝矩形线圈的用线量,改变矩形线圈的长宽之比β,可得到矩形线圈互感值取极大值所对应的长宽比。取原副边磁耦合机构高度为h=0.1 m,原边长导轨线圈的长为3 m,宽为0.25 m。副边单匝线圈用线量C为1 m,图10(a)所示的互感值随副边方形线圈SQ长宽比的变化曲线如图11所示,图10(b)所示的互感值随副边线圈SDD长宽比的变化曲线如图12所示。
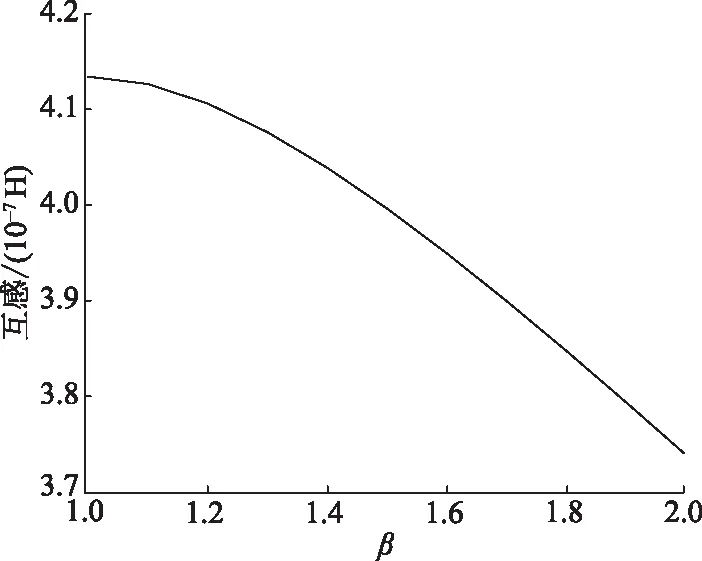
图11 矩形线圈互感值随长宽比的变化曲线

图12 DD型线圈互感值随长宽比的变化曲线
上述副边线圈SQ和SDD在固定用线量下优化原副边互感,分别得到当SQ、SDD长宽比β为1、1.6时,原副边互感取极大。现在改变副边单匝线圈用线量C,得出副边矩形线圈SQ与原边线圈之间互感值极大值和其所对应的副边线圈长宽比值,以及副边线圈SDD与原边线圈之间互感值极大值和其所对应的副边线圈长宽比值,相应曲线如图13所示。
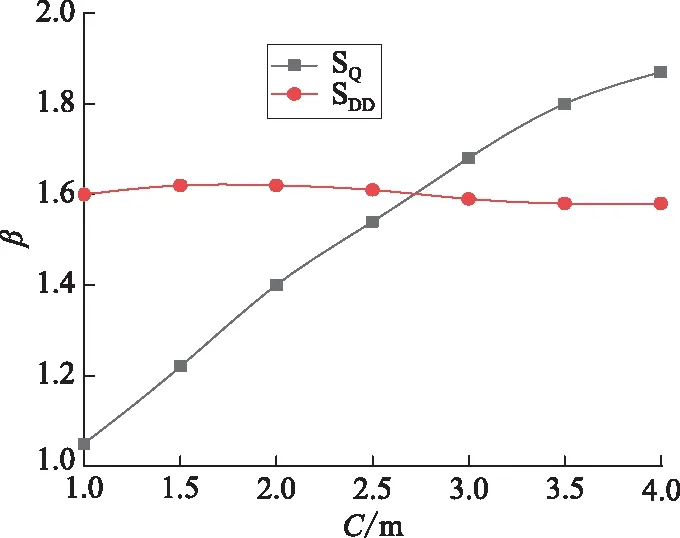
图13 互感极大值所对应的线圈尺寸比变化曲线
由图13可得,固定原副边磁耦合机构高度和原边长导轨线圈的长宽,单匝线圈用线量C变化时,副边磁耦合机构中DD型线圈SDD与原边长导轨线圈之间互感值极大值所对应的副边耦合机构长宽比值β几乎不变,而副边矩形线圈SQ原边长导轨线圈之间互感值极大值所对应的副边耦合机构长宽比值β随单匝用线量而增加,综上,本文选副边磁耦合机构的长宽比β为1.6。
3.3 基于最优尺寸比下的磁耦合机构尺寸优化
当副边磁耦合机构的中心点从第一个原边长导轨线圈中心移动至两长导轨线圈交接处时,原副边磁耦合机构的互感存在极大值、极小值,分别位于P点(Δy为互感极大值点到导轨间距离)、V点(两导轨间),具体位置如图14所示。
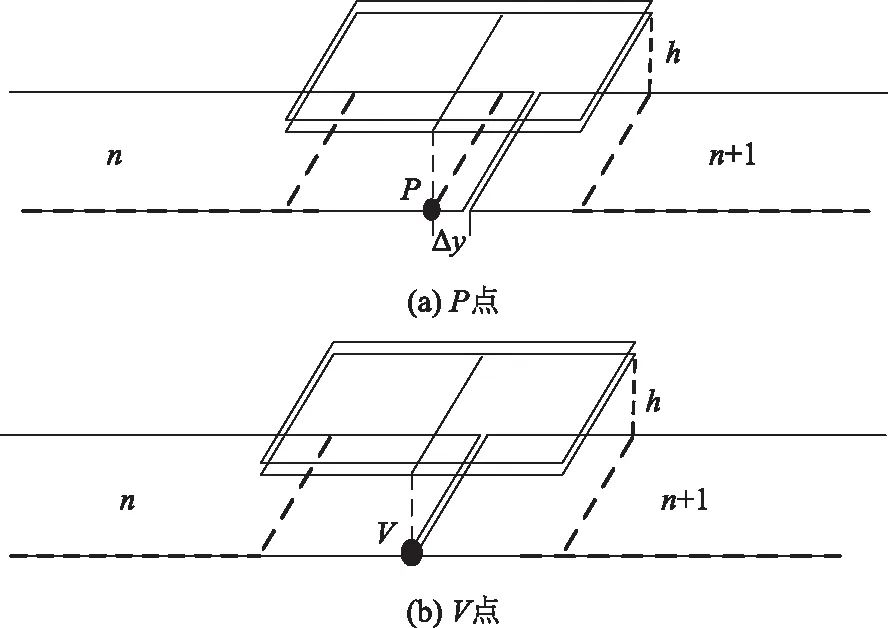
图14 P点和V点所对应的磁耦合机构位置示意图
记P点和V点间互感值变化率
(29)
式中MP和MV分别为原副边线圈在P、V点处的互感值。
本文选取原边线圈长边长为3 m,宽为0.25 m。由前文分析可知β值最优取1.6,原副边线圈高度h为0.1 m,改变原副边线圈的宽b,得出P点和V点间互感值变化率δ关于原副边线圈宽b的变化曲线,如图15所示。
从图15中可以求出P点和V点间互感值变化率δ的极小值以及对应的原副边磁耦合机构宽b的取值,b=0.254 m。
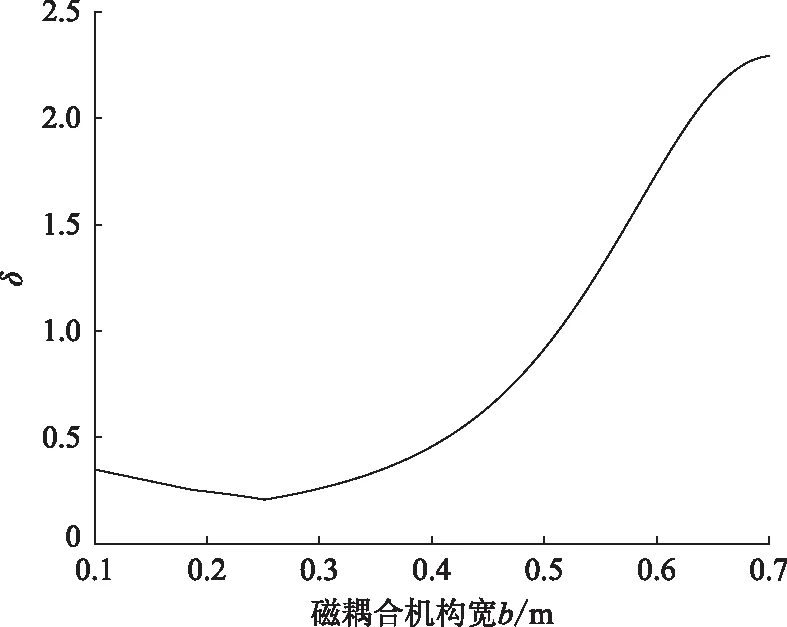
图15 互感值变化率δ关于线圈宽度b的变化曲线
综上所述,本文分段导轨式动态无线充电磁耦合机构的设计优化步骤流程图如16所示。
3.4 磁耦合机构的仿真分析
磁耦合机构的结构参数见表1。
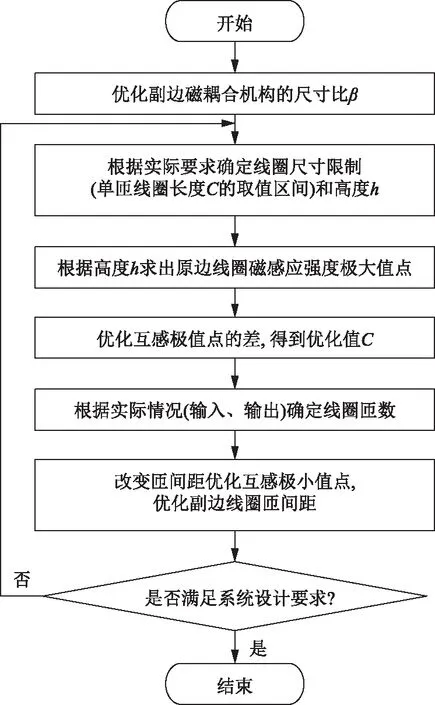
图16 磁耦合机构设计流程

表1 磁耦合机构仿真结构参数
利用有限元仿真软件求解副边磁耦合机构由一个原边长导轨线圈中间位置移动至相邻另一原边长导轨线圈中间位置过程中,原边磁耦合机构与副边磁耦合机构各线圈之间的互感值,如图17所示,图中:MP-Q为原边磁耦合机构与副边主线圈的互感值,MP-DD为原边磁耦合机构与副边DD型辅助线圈的互感值,MP-DDQ为原边磁耦合机构与副边磁耦合机构的互感值。其中,原边长导轨线圈同一时间只有一个导通,当副边磁耦合机构移动至原边两长导轨线圈交接处时,前一线圈断开,后一线圈导通,以单个原边长导轨线圈边缘为零点,取原边长导轨线圈的长为3 m。结合系统设计要求,选择线圈匝数为5,此时磁耦合机构的互感值为MP-DDQ=8.055 μH。
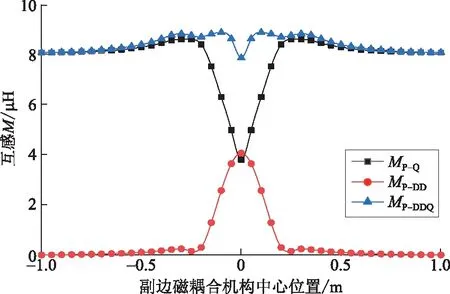
图17 磁耦合机构的互感仿真变化曲线
4 实验验证
为验证磁耦合机构设计优化的正确性,按照表1参数绕制线圈,利用阻抗分析仪测量参数值。固定原边线圈的位置,以原边两线圈交接处为起点,向两侧移动副边磁耦合机构,由于起点两侧测量互感曲线是对称,因此实际测量中只测量计算了副边磁耦合机构从0以0.1 m为步长移动至1 m所对应的互感值。绘制如图18所示的磁耦合机构互感仿真值与实测值的对比图。由图18可知,实际测量曲线和互感仿真曲线有较好的一致性,实验测量中的互感相较于仿真值波动误差不大于4.7%。
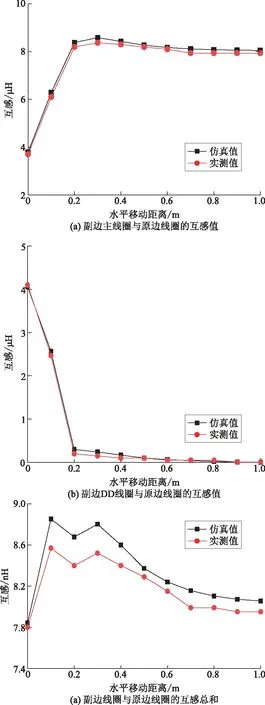
图18 磁耦合机构互感仿真值与实测值
为验证理论和仿真的正确性,利用上述绕制的磁耦合机构搭建系统功率为200 W的实验平台,如图19所示。
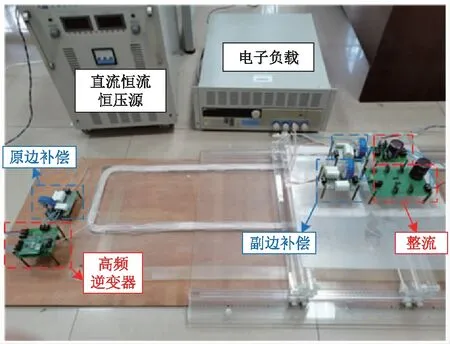
图19 实验平台
实验参数见表2,表中:Ud为直流源输出电压,LP、RP原边发射线圈自感、内阻,CP、C1、L1为原边发射电路LCCL补偿拓扑中的电容、电感,LSQ、RSQ为副边矩形接收线圈的自感、内阻,CSQ、C2Q、L2Q为副边矩形接收线圈LCCL补偿拓扑的电容、电感,LSDD、RSDD为副边DD接收线圈的自感、内阻,CSDD、C2DD、L2DD为副边DD接收线圈LCCL补偿拓扑的电容、电感,f0为逆变器工作频率,RL0为系统负载。
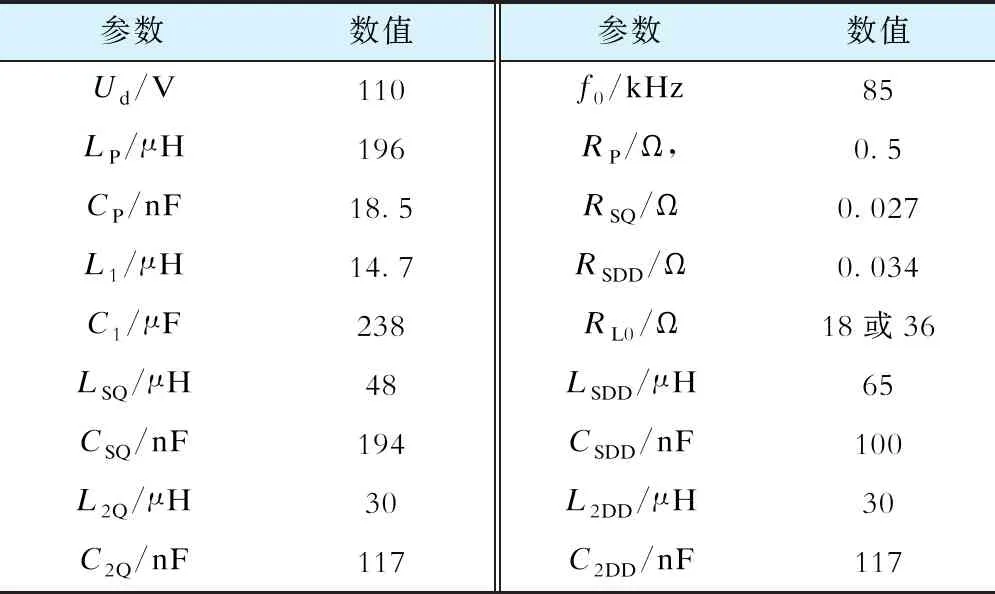
表2 实验平台参数
电子负载阻抗设置为18 Ω,测得逆变器输出电压和电流波形以及系统输出电压,逆变器的输出电压波形和电流波形同相位,系统处于完全谐振状态,输出直流电压为59.8 V。在某一时刻,将负载从18 Ω切换至36 Ω,系统的输出电压有微小波动,很快稳定,恒压模式下在负载切换后,系统输出电压有较小的波动,系统具有较好的负载无关性。
当负载为18 Ω时,移动副边磁耦合机构,通过功率分析仪读取系统输出电压及系统效率,绘制如图20所示曲线。
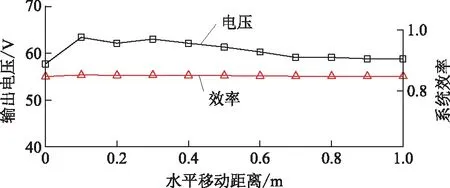
图20 系统输出参数随副边移动的变化曲线
由图20可得,本文的双接收动态无线电能传输系统的输出电压在58~65 V之间,电压波动范围在8.3%以内;系统的效率受互感波动的影响较小,副边磁耦合机构移动中,系统效率保持在85%左右。
5 不同系统比较
不同系统间参数比较见表3。文献[21]中原副边采用串联电容补偿(series and series ,SS),原边设计为长导轨式,采用多副边接收,保持输出电压的稳定性,但原边线圈一直工作,造成能量浪费;文献[22]中采用恒压恒流输出模式,原副边采用电感、电容、电容(双边LCCL)补偿,原边采用阵列式线圈进行发射,一定程度上增加了系统的设计难度;文献[23]采用恒压输出(LCCL-S)补偿,根据原副边的实时互感来调节线圈中的电流,使系统效率高和输出电流稳定,但需要实时对互感进行监测,系统控制比较复杂。
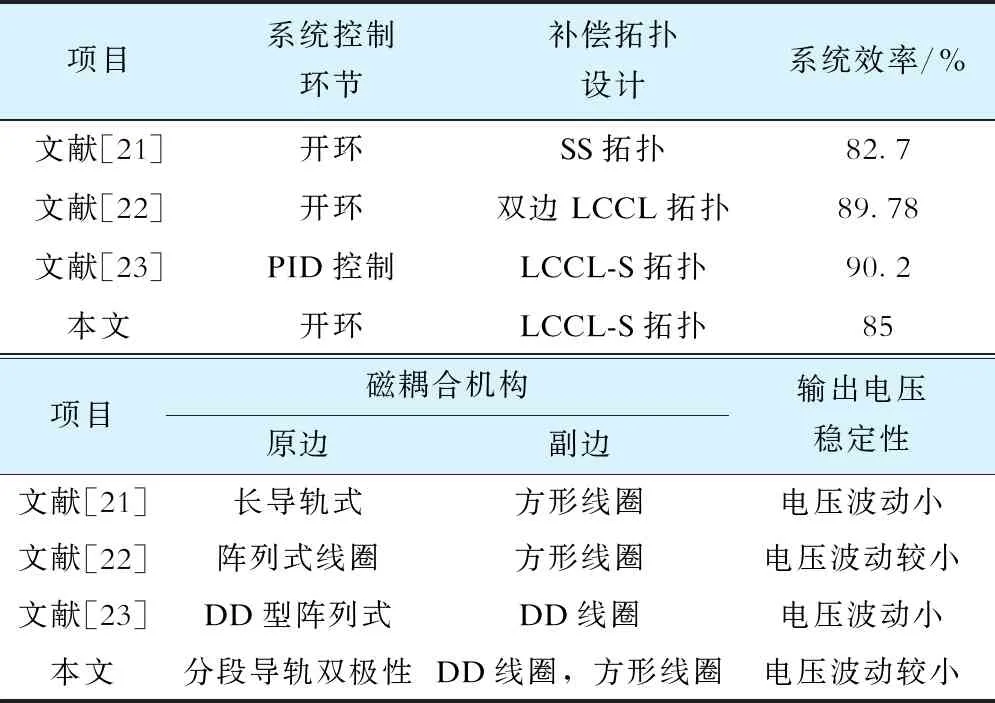
表3 不同系统间参数比较
6 结束语
本文针对分段导轨式动态无线充电过程存在的互感波动所带来的输出电压波动问题,研究一种组合型副边接收线圈结构。双接收线圈经独立的拓扑补偿后串联输出,可实现副边两接收线圈与原边的互感值之和为定值时,系统输出电压保持恒定。对磁耦合机构进行优化设计,得出最优的副边线圈尺寸比,基于最优尺寸比进一步优化线圈单匝用线量,降低磁耦合机构的互感波动,最后通过仿真和实验证实了磁耦合机构优化方法和双接收回路设计方法的可行性。本文优化后的磁耦合机构互感波动率相较于仿真误差在4.7%以内,开环状态下系统的输出电压波动在8.3%以内,效率保持在85%左右。

