基于机器学习的操作系统故障自动诊断方法
卢士达,刘文意,王亮,宋轶慧,方晓蓉
(国网上海市电力公司信息通信公司,上海200122)
1 引言
因为传感器网络内节点个数较多,且拥有较高水准的自主性,各个传感器节点的能力与能量都极其有限。若在恶劣的网络环境下,网络拓扑会一直处于高度动态变化中,所以创建有效的传感器网络是一项极富挑战性的工作[1]。在传感器网络中,操作系统是上层应用与协议运行的基础,运行在各个节点内,起到管理节点与网络内的软、硬件资源的功能,是影响全局网络优良的关键因素[2]。因此,对操作系统进行故障诊断是相当必要的环节。
关于操作系统故障诊断问题,文献[3]提出一种融合专家经验的序列数据趋势识别方法。该方法基于专家对趋势特征的描述,使用模糊矢量形式描述序列数据变化趋势,通过趋势识别决策树,实时判断数据趋势类型,提高故障诊断准确性。文献[4]提出一种基于光学灰度图像辨识的故障诊断方法。该方法按照实时监测数据构造系统运行状态图像,利用CCD 摄录方法截取灰度图像,从不同分辨率的系统灰度图像近似直方图中提取系统灰度图像特征。将这些特征和标准特征间的欧式距离对比,把目前状态划分成相距最小的标准特征类。但上述方法均无法较好适用于操作系统故障诊断中。
因此,本文提出一种基于机器学习的操作系统故障自动诊断方法。通过建立基于AR-连续HMM的操作系统故障诊断模型,大幅提高诊断精确性,分析机器学习机理与优势,构建自组织竞争神经网络,并代入相似性图方法,得到高效率、高准确性的操作系统故障自动诊断模式,增强操作系统使用流畅性,为用户提供更为优质的网络服务。
2 基于AR-连续HMM 的操作系统状态分析
隐马尔可夫模型(Hidden Markov Model,HMM)可通过系统内各项因素来全面分析运行状态,其中,N表示模型内马尔可夫链的状态个数,把t时段马尔可夫链的状态描述为qt。M是各个状态相对的可能观测值,M个观测值是V1,V2,…,VM,t时段的观测值是Ot,且Ot∈(V1,V2,…,VM)。π是原始概率分布向量,将其定义为:

式中,

A代表状态转移概率矩阵:

式中,

B是一个观测值概率矩阵,B=(bjk)N×M,且:

关于连续HMM,B为观测值概率函数,将其记作:

因此,可以把HMM定义成λ=(N,M,π,A,B),同时化简成:

固定模型λ所生成的某个观测值序列O的概率,即为模型λ与状态序列S同时产生的联合概率:

模型λ的参数估计可运用极大似然方法进行计算:
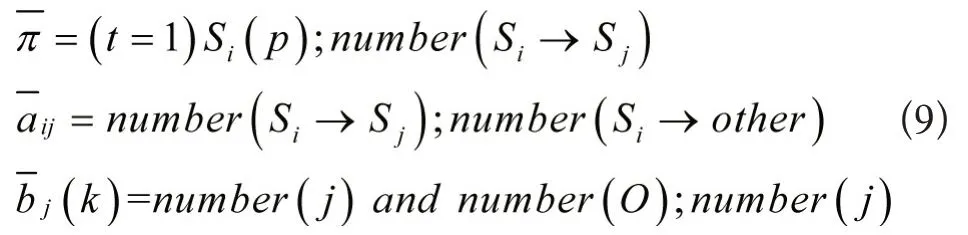
在t=1 时刻,处于状态Si的概率;从状态Si转移到Sj的平均次数。
从状态Si转移到Sj的平均次数,从状态Si转移到其他状态的平均次数。
处于状态j和出现观测O的平均次数;或者单独处于状态j的平均次数。
给予一个固定观测值序列O,HMM的训练通过原始模型完成,利用极大似然估计方法[5],逐渐更新模型参数,提高观测序列概率,最后约束条件为P(O|λ)的值为最大。
操作系统振动序列可呈现出随机时序xt的观测值,这与其本身的前一个或前几个时段观测值相关[6],将此种随机序列的前后时段关联性,采用线性回归模型的随机差分解析式进行描述,具体记作:

由此,把线性自回归模型AR(p)的参变量φj当作振动信号特征值。特征提取详细流程为:首先把信号零均值进行归一化处理,将相等长度预处理之后的振动信号分割成T段,对各段提取25阶自回归模型的参变量φj,把该特征值当作系统状态观测值,构成完整的观测序列。
为了更好地完成操作系统故障自动诊断,就要构建持续高斯密度混合HMM 模型,Markov 链是5 状态左-右型,状态原始概率是:

各个状态的观测概率是通过两个高斯概率密度函数综合判定的,该观测值概率密度函数是:
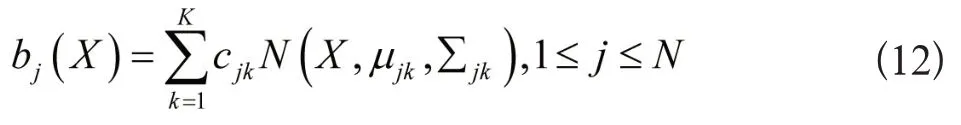
其中,N(X,μjk,∑jk)代表多维高斯概率密度函数,μjk是平均值向量,∑jk是方差矩阵,K是构成bj(X)的混合概率密度函数数量,cjk表示组合系数,并符合以下条件:

为了增强故障诊断模型的平稳性,采用数量较多的观测值序列进行模型训练[7],校正后的计算表达式即为故障诊断模型的最终形式,将其记作:
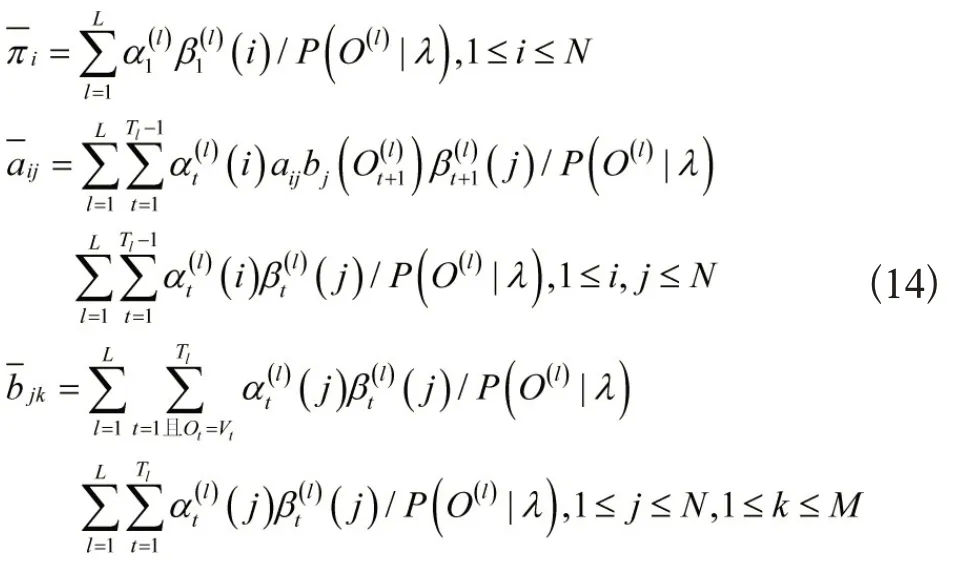
其中,α是前向变量,β 是后向变量,L是观测值序列个数。
3 机器学习下操作系统故障自动诊断
3.1 机器学习下故障模式区分
机器学习是现阶段人工智能领域内发展最迅猛的学科之一,它能运用已有的经验改进操作系统的全局性能。机器学习的定义是:针对某种任务T与性能度量P,假如一个计算机程序使用经验E在任务T内用P来衡量的性能获得提高。
现有的操作系统故障诊断技术,在面向日益繁杂的网络环境时,均存在诊断知识很难获取及更新缓慢的缺陷。但基于机器学习的故障诊断却具备超强的学习能力,不但能够从复杂的网络环境内自动学习诊断知识,还可以完成自身更新,继而改进自身性能,更好地服务于网络故障诊断[8]。基于机器学习的网络故障诊断关键集中在人工神经网络、支持向量机两种诊断方法。因为人工神经网络拥有优秀的非线性拟合性能,因此本文使用人工神经网络来完成操作系统故障自动诊断目标。
在诸多人工神经网络模型中,最常见的为误差反向传播神经网络,即BP 神经网络。BP 神经网络是一种单向传播的多层前向网络,包括输入层、隐含层与输出层。其学习模式是一种有监督学习,在输出层对比网络真实输出与相对预期输出的偏差均方差,假如无法获得满意的偏差准确度,使用梯度下降法调节每层神经元权重,最后让偏差为最低。
本文把自组织竞争神经网络引入操作系统故障识别中。自组织竞争神经网络内仅有输入层与竞争层组成的两层网络,不包含隐藏层,具体参见图1。它是一种使用无监督学习模式的神经网络,不需要预先明确标准形式,网络经过Kohonen规则对输入层实施自适应学习与类别区分,同时把标准形式利用权值矩阵的行混合网络相融合。
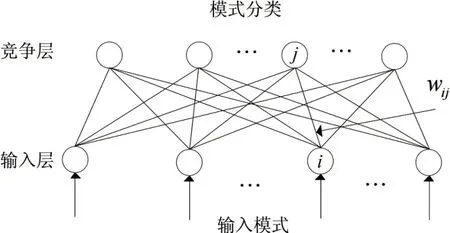
图1 自组织竞争神经网络示意图
自组织竞争神经网络的基础思路为:网络竞争层每个神经元竞争对输入矢量的响应机会,最后只有一个神经元为获胜者。则和获胜神经元相关的每个连接权值会向更有利于其竞争的方向进行转变,获胜神经元就是输入矢量的分类。把竞争层的输出过程记作:
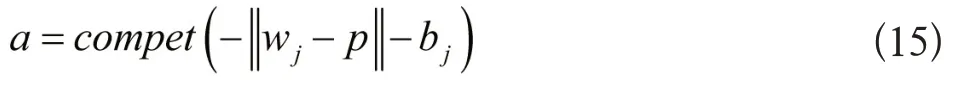
其中,p 代表输入矢量,wj、bj分别为j神经元的权值矢量与域值。
竞争层的传输函数compet是一个二值函数,该函数把最大输入神经元的输出设定成1,其余全部神经元的输出均是0。域值是用于调节神经元的获胜概率,利用降低此神经元域值来提高其获胜几率。与此同时,域值也能增强经常获胜的神经元临界值,令其获胜概率明显减小。修正与获胜神经元连接的权值,其余连接权值维持原样。权值校正方程为:

式中,l 代表学习速度,体现出学习时连接权值的大小。通过上述过程可知,自组织竞争神经网络能够有效完成故障的模式区分,为故障诊断提高先决条件。
3.2 基于相似性图的故障自动诊断方法
为了进一步提高操作系统故障诊断的及时性,使用基于相似性图的故障自动诊断,具体过程如下。
图2是故障自动诊断的架构图,架构图内包括离线模型训练与在线故障诊断。若两个组件是相互关联的,在两个指标之间构建一个连接,连接权重是两个指标的相关度。建立替代图的目的是:假如明确某个时间与某个故障具备关联,则其余时间对该故障识别没有任何作用;假如没发生和故障相关的事件,而发生了代替图内的其他事件,则同样证明可能产生故障。
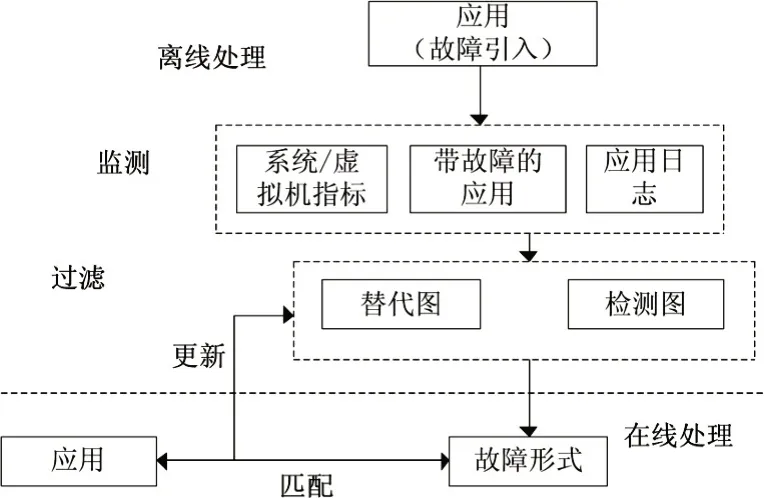
图2 故障自动诊断架构示意图
组件之间的相关度包含:若两个事件用固定的次序实现,则两个事件是相关的;若探测指标X是Y的一部分,则两个探测指标是相关的;若探测指标X抵达临界值后产生Y事件,则探测指标X与事件Y相关。
如果两个组件分别是X、Y,使用NMI推算两个组件的相关度:

式中,H(X)、H(Y)均为Shannon信息熵,I(X,Y)是参变量之间的相关度。算出随机的组件对NMI 值后,就会得到其相关性矩阵。
获得相关性矩阵后,对有关探测指标与事件实施分组。此方法对相关性矩阵进行聚类分析,把各个探测指标与事件当成一个分组,使用迭代模式对最接近的分组进行融合,最后随机两个分组之间的相关度均低于事先定义的临界值时,分组算法结束。
在操作系统中,以上组件之间的架构不会产生任何变化,但因为用户行为的改变致使以上分组的稳定性较差。比如,在数据库服务器处理数据包请求的过程中,系统占据较多的CPU,而处理本地文档复制会占据相当大的内存。在这两类操作中,操作系统内包含不变量,使用一致性分数来描述分组在两种操作行为下的不变量,其公式为:

式中,C代表某个分组,n是此分组内的关联数量,ni代表第i个关联出现的次数。式(19)代表两个操作行为内没有不变量。所以可以看出,相同分组内的探测指标与事件能够互相替代。
操作系统内的故障是一系列事件的集合,不同的事件在故障诊断内拥有不同权重。把事件集合根据逻辑与事件关联组成一个有向图,同时使用有相同内容的关键事件来描述故障形式。因为操作系统中涵盖数量众多的监测数据,关键事件构成的故障形式能够极大提升故障诊断速率。
在关键事件的诊断过程中,首先使用有向图描述事件和故障形成的关联。假如事件A先于事件B发生,则A至B具备一条有向边。在创建有向图时,一条终点是故障的路径即为一个系统故障。根据事件在指定故障路径内出现的次数,把事件划分成极其活跃、活跃、一般与不活跃四种类型。为了完成故障自动诊断目标,使用社会网络影响力排名对事件的关键性实施排序。在创建完毕的有向图内,在亲密度、权重与时间延迟下,对事件的关键性进行排名。
在故障F内,事件e的亲密度是:

式中,#e为e在F内出现的次数。
事件e的权重是时间故障路径数量的倒数,具体记作:
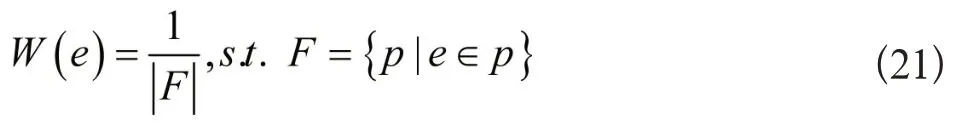
在故障F内,事件e的时间延迟表示此事件持续时间的指数函数:

式中,α、β均为指数函数参变量。
最后按照事件的亲密度、权重与时间延迟,对事件关键性实施排名,具体过程为:
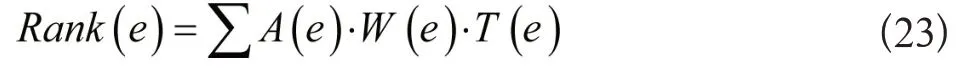
对故障事件进行排名后,把排名值Rank(e)最高的时间当作关键事件,同时实现准确高效的操作系统故障自动诊断。
4 仿真实验
为了验证本文方法性能优越性,与文献[3]、文献[4]方法进行仿真对比实验。在操作系统正常运行时,对系统引入故障来判别三种方法性能优劣。实验使用的评估标准是AUC、AUC的值越高,表明方法的故障检测效果越佳。在实验中,依次考虑故障已知与未知两种状态。实验结果如图3所示。
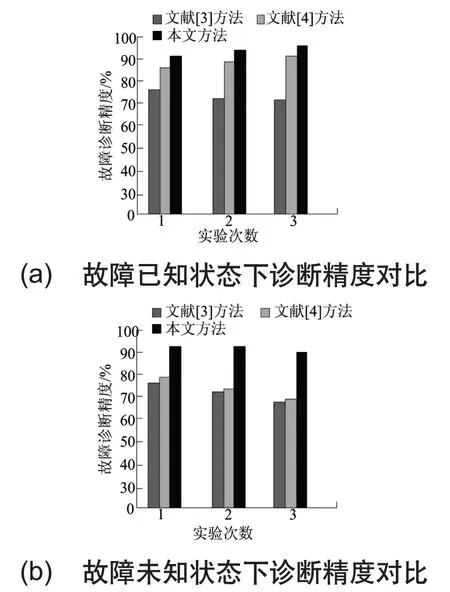
图3 故障已知、未知状态下故障自动诊断精度对比
从图3中可知,本文方法的AUC 均为最高的。在故障已知状态下,文献[4]方法与本文方法相差不多,但远优于文献[3]方法,原因在于文献[3]方法对故障诊断存在较强主观性,稳定性不高;在故障未知状态下,所提方法的故障检测精度均优于两种文献方法,这是由于本文方法使用机器学习模式下的故障诊断方法,摆脱了诊断知识很难获取及更新的缺陷。
图4是三种方法的召回率和错误检测率的关联结果。
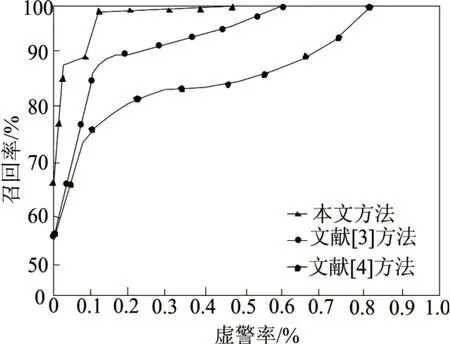
图4 召回率和错误检测率的关联示意图
从图4中可知,伴随错误检测率的提升,召回率逐步变大。本文方法的曲线在最上方,文献[3]方法的曲线在最下方。证明在同样错误检测率情况下,本文方法召回率最高,原因在于本文方法运用相似性图法提升了故障诊断精度,使故障自动诊断性能更优,鲁棒性更强。
5 结束语
为了深入优化操作系统的性能,本文基于机器学习对操作系统故障进行自动诊断,建立AR-连续HMM 操作系统故障诊断模型,增强诊断精确性。引入相似形图方法,完成高精度故障自动诊断目标。将所提出的诊断方法应用于计算机操作系统的故障诊断,可以提高系统的应用性能,降低操作系统的故障发生率,有利于帮助操作系统更好地运行。

