考虑无功补偿的中/高压配电网双层协调控制方法

毛彦伟,陈晓宇,吴佩莹,陈佳明,郑旭初

（1．绍兴大明电力设计院，浙江绍兴 321000；2．浙江优能电力设计有限公司，浙江宁波 315000）

1 引言

最近几年以来，配电网分布式电源中可再生资源渗透率以及电子设备数量持续增加，如果大量的分布式电源接入配电网后，会导致接入点电压持续下降，网损会随着电压的下降而增加，控制误差也会随之增加。现阶段，配电网双层协调控制问题已经成为当前研究的热点话题。相关专家针对中/高压配电网双层协调控制技术方面展开研究，例如庄慧敏等人[1]设定网络损耗为最小目标函数，以此组建优化模型，利用二阶锥规划算法对模型求解，实现配电网外层控制；内层控制以外部控制步长的关键点进行在线优化控制，有效抑制关键节点的电压波动。吴晓飞等人[2]分析通信网络中光伏逆变器的无功电源，组建电压区分以及主导节点选择模型，设计上层全局优化以及下层分区优化的双层协调控制策略。虽然以上方法取得了十分满意的研究成果，但是由于没有针对无功补偿方面的内容展开研究，导致系统电压水平与网损不能达到实际应用所需要的水平，控制误差仍需大幅度降低。为了使上述问题得到有效解决，设计并提出一种考虑无功补偿的中/高压配电网双层协调控制方法。

2 中/高压配电网双层协调控制

2.1 控制模型构建

无功补偿主要是指电力系统在运行过程中，采用并联的方式实现电能输出。在进行系统设计的过程中，大部分通过无功补偿方式确保系统的运行[3-4]，但是这样会导致配电网负载经常感觉到系统存在阻抗。

为了确保电压系统的稳定性，需要使无功功率达到平衡稳定的状态，同时还需要注意电网运行过程中无功备用容量。以下分析无功补偿对电网的作用：

(1)无功补偿能够稳定电压[5]，同时提升电力系统的供电质量。

在进行无功补偿前，电压损耗△U为：

上式中，UN代表电力系统线路末端电压值；R代表电力系统线路等值电阻值；X代表电力系统线路等值电阻；P代表电力系统线路末端有功负荷；Q代表电力系统线路末端无功负荷。由公式(1)可知，在求解出参数P、X后，能够将损耗问题转换为有功功率或者无功功率问题，在此研究中将其设定为有功功率[6-7]。

上式中，PL、QL分别表示三相交流系统的有功功率与无功功率。在安装电容之后进行无功补偿，线路电压损耗计算公式为：

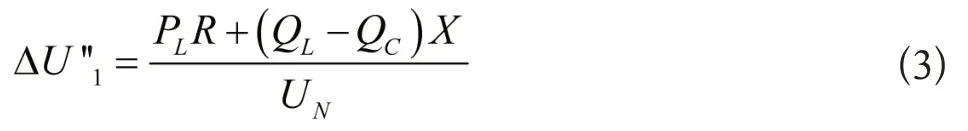
上式中，QC表示无功补偿容量。由公式(3)可知，电压损耗的变化实质就是通过降低无功功率完成电力系统的无功补偿[8]。补偿前后的电压损耗对比值为：

从公式(4)可知，电压损失的变化和无功补偿量的大小是呈正相关的。

(2)提升功率因素，降低功率损耗：

采用公式(5)表示功率因数：

在对电力系统进行无功补偿时，电力负荷呈感性特性状态，这主要是由于电压分量高于电压矢量造成的。为了有效解决该问题，需要提升功率因数，当无功补偿容量为QC时，功率因数的计算式如下：

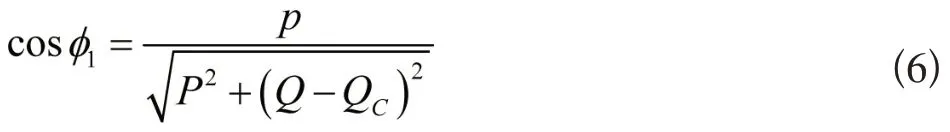
对电力系统进行无功补偿时，需要降低线路的负载损耗[9]。在配电的过程中，会出现电压偏差大以及线路损耗较大等情况。为了保证电力系统稳定完成无功补偿，需要优化配电网无功功率，使中/高压配电网的内部功率达到均衡的状态。

三相交流功率的计算式为：

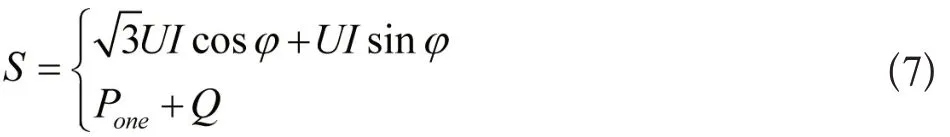
上式中，S代表三相交流系统的无功功率；Pone代表三相交流系统的有功功率；I代表线电源。

在未进行无功补偿前，线路上的有功损耗为：

此时线路上的无功损耗△Q表示为：

在线路末端进行容量为QC的无功补偿时，线路损耗△P＇为：

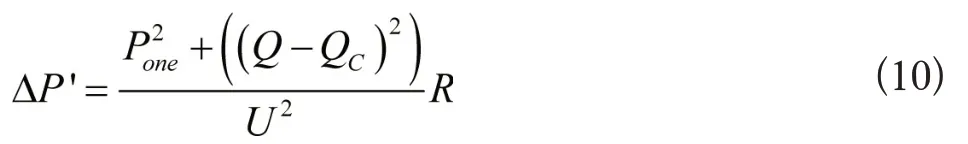
补偿前后进行对比，有功损耗的下降值为：

变压器的有功损耗计算式为：

变压器的无功损耗QT能够表示为以下的形式：

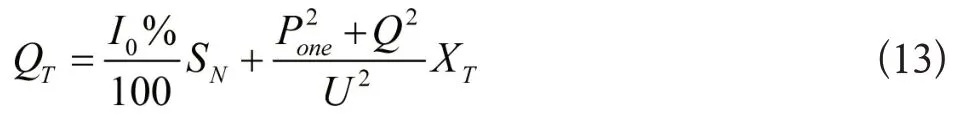
PT和QT的后半部分为负载损耗，则补偿之后的负载损耗可以表示为：

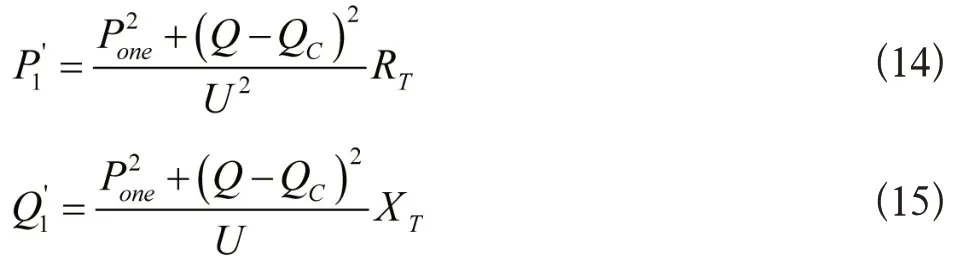
在配电网中，由于大部分线路在运行的情况下是感性的，在只考虑电压的条件下，需要通过潮流实现电压在纵分量的损耗，具体的计算式如(16)所示：

变压器的电压损耗计算式为：

结合以上分析，获取最佳无功补偿方式。同时根据确定配电网无功电压补偿多种优化指标，构建中/高压配电网双层协调控制模型，模型具体的表达式为：

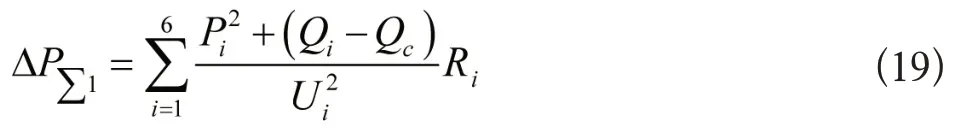
2.2 中/高压配电网双层协调控制模型求解

分布式电源在接入配电系统后，系统的运行状态会受到各种因素的影响。以实现最小电压偏差为目标，设定中/高压配电网双层协调控制的目标函数为：

上式中，Vi表示节点电压，VN表示节点平均电压，Vilim代表节点电压的期望值，即：

当系统在接入电子设备以后，系统内部功率波动较为明显。为了有效保证系统的稳定运行，需要综合考虑状态变量不等式约束：

声呐分辨力是指在多目标环境下对相邻2个目标的最小可分辨能力，一般按照目标的方位、距离、速度和加速度等参数来分辨，其中距离分辨力和速度分辨力仅取决于信号的形式及其参数。在采用匹配滤波的条件下，模糊函数是与目标距离和速度有关的信号回波通过匹配滤波器之后的输出[2]，可用来衡量信号对具有不同距离和不同速度的2个目标的分辨能力。当目标相对静止时，回波信号仅体现出时间延迟和衰减;当目标相对运动时，回波信号还会产生多普勒频移和时间上的压缩或展宽。

在上述分析的基础上，采用模拟退火粒子群算法对2．1小节所组建的模型进行求解，具体的求解步骤如下所示：

(1)将算法中各个参数分别进行初始化处理，其中c1、c2为学习因子，Pc为算法中各个参数的交叉概率，Pm为变异概率，λ为粒子温度冷却系数，tmax为算法的最大迭代次数。

(2)由N个粒子随机组成种群，同时对粒子的位置以及速度进行初始化处理。

(3)计算粒子适应度值，评价粒子适应度值，同时将计算结果放置于pibest中，对比不同粒子的适应度值，将最优适应度值放置于pgbest中。

(4)分别计算不同的粒子的初始问题，具体的计算式如下：

(5)更新不同粒子的位置以及适应度值。

(6)通过交叉概率对下一代种群中的粒子进行交叉运算，通过模拟退火思想判定是否接受新一代的粒子，对交叉计算结果进行优化处理，其中判定公式为：

(7)经过步骤(6)进行交叉运算后，形成全新的粒子个体，利用变异概率进行变异计算，结合模拟退火思想判定是否接受新一代的粒子。

(8)将公式(26)作为模拟退火算法判定过程的主要依据：

(9)当算法没有达到设定的迭代次数时，进入步骤(5)重新进行计算；当算法达到迭代次数后，输出优化结果，获取最优中/高压配电网双层协调控制方案。

3 仿真实验

为了验证所提出考虑无功补偿的中/高压配电网双层协调控制方法的有效性，进行仿真测试。实验在电力系统接入位置随机选取15个节点，设定有功出力为0．1p．u，功率为1．0，初始电压为1．0V。

(1)电压/(V)：

利用表1给出三种不同方法的节点电压变化情况。

分析表1中的数据可知，所提方法在进行无功补偿后，相比另外两种方法，电压水平得到明显提升。

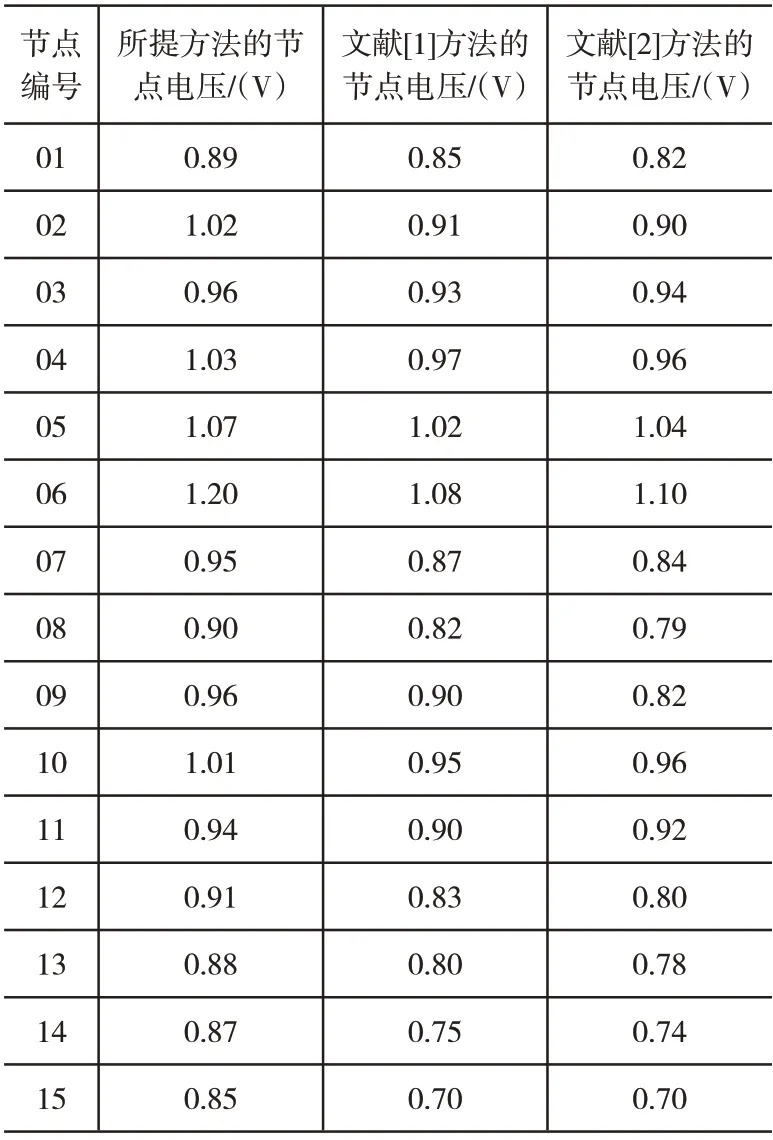
表1 不同方法节点电压变化情况

(2)网损/(p．u)：

利用图1给出三种控制方法的网损变化情况：

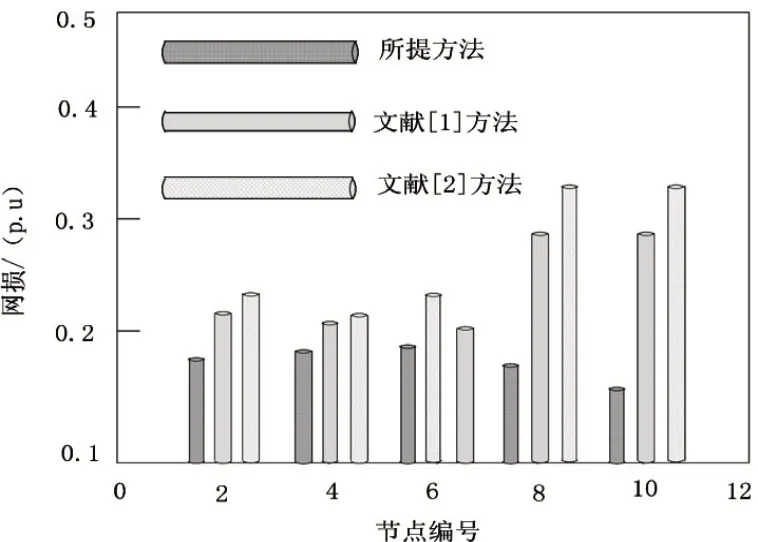
图1 不同方法网损对比结果

分析图1中的实验数据可知，与另外两种方法相比，所提方法的网损明显更低一些，主要原因是：所提方法在进行无功补偿以后，有效提升高端电压，当电压上升后，网损得到有效降低。

(3)控制误差/(%)：

控制误差指的是双层配电网中，上、下层控制参数与双层配电网协调控制规定参数的比值。将控制误差作为评价指标，其中控制误差越低，则控制结果越理想；反之控制误差越高，则控制结果较差。控制误差的计算公式为：

其中，Kχ表示上层配电网协调控制参数，Kμ表示下层配电网协调控制参数，Ks表示双层配电网协调控制规定运行参数。利用表2给出具体的实验结果：

表2 不同方法控制误差对比结果

由表2中的实验数据可知，在三种方法中，所提方法的控制误差最低。当所提方法的电压水平得到有效提升以及网损得到有效降低后，促使所提方法的控制误差得到明显改善，能够获取最佳控制方案。

4 结束语

针对传统方法存在的一系列问题，设计并提出一种考虑无功补偿的中/高压配电网双层协调控制方法。仿真实验结果表明，所提方法能够有效降低控制误差以及网损，提升系统电压水平，有效实现中/高压配电网双层协调控制。