基于VMD-维纳滤波的时间序列去噪
汪春华,冯焱侠
(1.西安航空学院电子工程学院,陕西西安 710077;2.西安理工大学自动化与信息工程学院,陕西西安 710048)
1 引言
时间序列分析方法在金融、工业领域的数据分析中具有重要的应用价值。该方法根据系统有限长度的观察数据,建立可反映序列中隐含的动态依存关系的数学模型[1-2]。然而常见的时间序列具有一定的随机和波动性。随机性一般可看作是噪声干扰项,通常认为是传感器产生的随机噪声。为了提高时间序列处理和分析的准确性,需要对噪声进行去除。
时间序列中的去噪方法包括传统的中值滤波、均值滤波以及维纳滤波、卡尔曼滤波等。其中维纳滤波和卡尔曼滤波基于时间序列的自相关性,具有较好的去噪效果,但仅适用于平稳时间序列。小波变换也可用于噪声的去除,通过对序列进行时间尺度的分解,寻找不同时间尺度下的特性,具有较高的准确性,其缺点是需要设定基函数[3]。
近年来,时间序列分解技术得到了广泛关注。这里,经验模态分解(EMD)将具有不同时间尺度的信号逐级分解,不需要复杂的递推迭代和矩阵运算,其缺点是易产生虚假分量和模态混叠等[4]。集合经验模态分解(EEMD)在采样频率较高时去噪性能优于EMD,缺点是存在端点效应等问题[5]。变分模态分解(VMD)采用非递归的形式,假设每个模态具有各自中心频率,寻找可再现输入信号所有模式的集合[6]。VMD分解的缺点是无法确定分解的模态,影响了时间序列分解的可靠性。
本文结合改进VMD 方法和维纳滤波实现时间序列随机噪声的去除。首先,提出基于余量序列和其它固有模态分量之间的互相关性,建立VMD 模态个数估计模型;其次,采用VMD方法对序列分解,实现平稳化并去除高频噪声;然后采用维纳滤波对各模态序列消噪;最后就仿真和实测数据对提出的去噪模型进行验证。
2 VMD分解
2.1 VMD原理
VMD 将原始时间序列数据分解为若干个固定模态分量(IMF),每个IMF 都为调频调幅子序列,将各个IMF解调到各自的基频带宽上以实现各个模态带宽之和最小,且满足模态重构组合之后近似等于原始信号[6]。VMD求解包括变分构造和变分求解.
a)变分构造
假设通过分解得到K个模态分量uk(t),k=1,2,…,K,以各个模态所占带宽之和最小为目标,寻找最优IMF分量。
1)对模态分量uk(t)进行Hilbert变换,得到各个IMF的解析信号和对应的单边谱:

其中,δ(t)表示单位冲击信号。
2)假设每个模态的中心频率为ωk,对其乘指数项使其频谱调制到各自的基频:
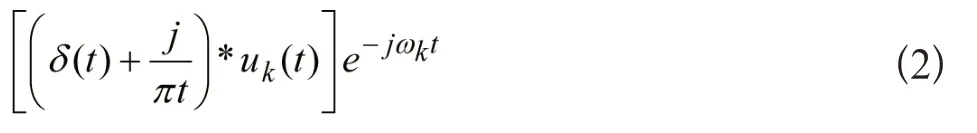
3)计算K个模态信号带宽,通过求解上述调制后信号梯度的2范数得到变分约束问题:
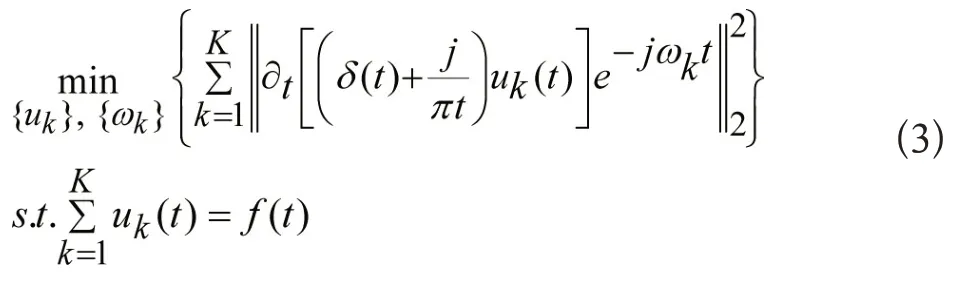
其中,ωk和uk(t)分别表示模态中心频率和模态分量IMF,f(t)表示原始信号。
b)变分求解
结合拉格朗日乘子法以及二次乘法算子交替算法,将变分约束问题变换成非约束问题,首先,对约束问题引入拉格朗日乘法算子θ(t)和惩罚因子C,则非约束问题如下:
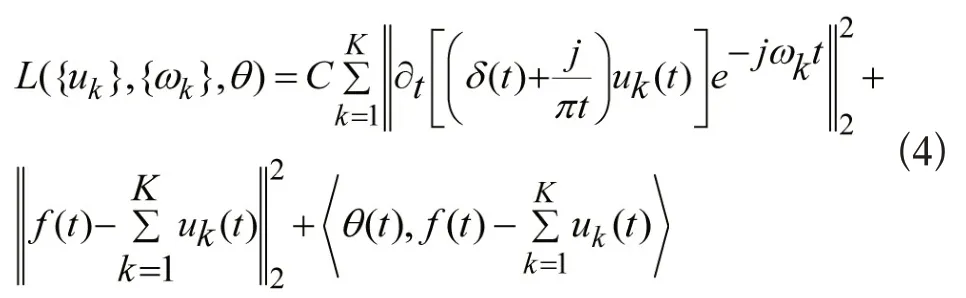
式中,惩罚因子可使信号重构时有较高精度,拉格朗日乘法算子使得约束条件更加严格。
对式(4)采用乘法算子交替算法进行求解,然后利用2范数下Parseval/Plancherel 傅里叶等距法变换到频域,最终可得到其二次问题的解为:
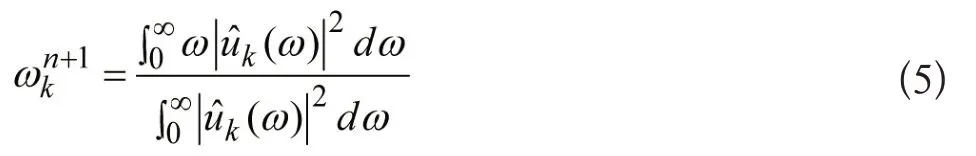
VMD中所求的各个模态和中心频率在频域内迭代,最终通过傅里叶逆变换从频域得到时域解;各个模态的中心频率作为其功率谱的中心,不断循环迭代[7-10]。这里,拉格朗日乘法算子的更新公式如下所示:

这里,当学习因子τ为非零值时,可保证得到的各个模态具有较高的重构精度。
2.2 改进VMD算法
作为一种非递归分解方式,VMD的分解模态个数需要人为设定,这种分解个数非自适应问题是VMD的一个缺陷。当设定的模态个数过小时,出现欠分解,信号中的多个时间尺度的分量可能出现在同一个模态中;反之当模态个数过大时,某个模态分量可能存在于多个模态分量中,出现频谱断裂现象。目前对于模态个数估计尚缺乏通用且准确的方法[11-12]。
互相关系数可以表示两个时间序列的相关程度。当两个时间序列相似度越高,含有的频率成分越接近,互相关系数越接近于1[13-18]。当分解模态个数最优时,使用VMD 对序列进行分解之后,得到的余量可视为噪声,除去余量的其它模态序列不具有高频噪声分量,且余量与其它IMF 之间不相关[19]。基于此,本文采用互相关系数来确定模态个数K。假设经VMD 分解得到的余量序列为c(n),其它模态分量重构的序列为f(n),则二者的互相关函数为:
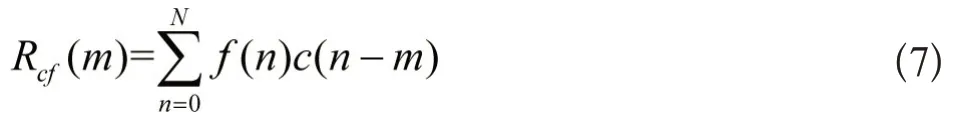
其中,N为序列模态个数,m为时间间隔。对Rcf(m)进行标准化得到标准互相关函数:
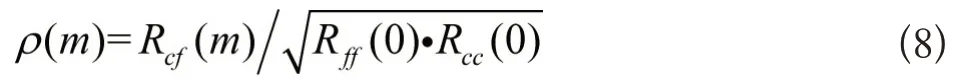
其中,Rcc(0)和Rff(0)分别为两个模态序列的自相关函数。由于时间间隔m为1时,序列之间的相关性最大,故本文取时间间隔m为1时互相关函数的值作为互相关系数,以此确定最优模态分解个数,即:
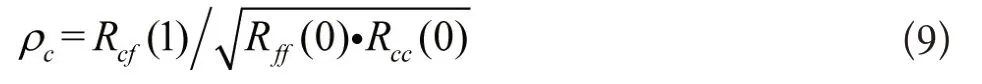
3 VMD-维纳滤波的去噪模型
3.1 维纳滤波
维纳滤波是基于最小均方误差基础上,基于时间序列相关性以及噪声与信号之间的非相关性设计滤波器。维纳滤波适用于加性噪声的去除,通过设计滤波器的传递函数使得输出尽可能接近原信号。维纳滤波器一般采用变换域求解方法,在最小均方误差基础上,求解传递函数。理论上,任何信号都可认为是白噪声产生的,如图1所示。假设白噪声的自相关序列为:

图1 信号的白噪声产生模型

则信号s(n)自相关序列的z变换为:

图2是维纳滤波的Z域求解框图。很显然,其滤波函数可写为:

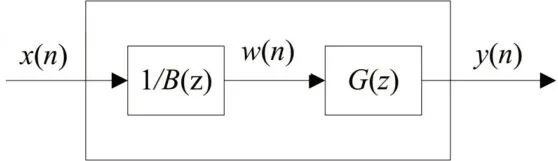
图2 维纳滤波的Z域求解
对于实际的因果信号,其最优滤波函数可写为:
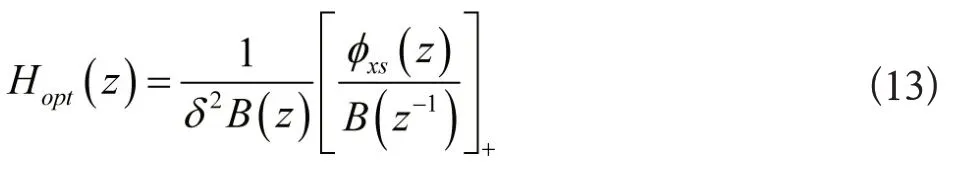
维纳滤波的优点是最小均方误差意义下的最优滤波器。其缺点是要求时间序列为平稳序列,对于非平稳信号的滤波效果较差。本文建立VMD-维纳滤波的去噪模型,首先采用VMD分解原信号,消除非平稳性,然后采用维纳滤波去噪。
3.2 预测流程
本文结合改进VMD 和维纳滤波实现时间序列去噪的流程如下:
1)采用互相关系数的计算公式(9),确定VMD 分解的最优模态个数。
2)采用VMD 对时间序列进行分解,实现平稳化并消除高频的余量序列。
3)采用维纳滤波的公式(13)对各模态序列分别进行滤波。
4)对滤波后的模态序列进行重构,即为去噪后信号。
4 结果与分析
选取平均绝对误差(MAE)作为评价滤波性能指标,如下所示:

式中,yi与分别表示原始信号和滤波后信号,N表示总的样本数。
通过仿真信号来验证本文提出方法的有效性。原信号包含四个不同频率的正弦信号,并添加一个均值为0方差为0.8 的高斯白噪声。然后,对该仿真信号进行VMD分解,当分解个数K依次为2,3,4,5,6,7,8时,不同K下余量与模态重构信号的互相关系数如图3所示。从图中可看到当K=7时,互相关系数均为最小值,因此最优的模态个数设为7。
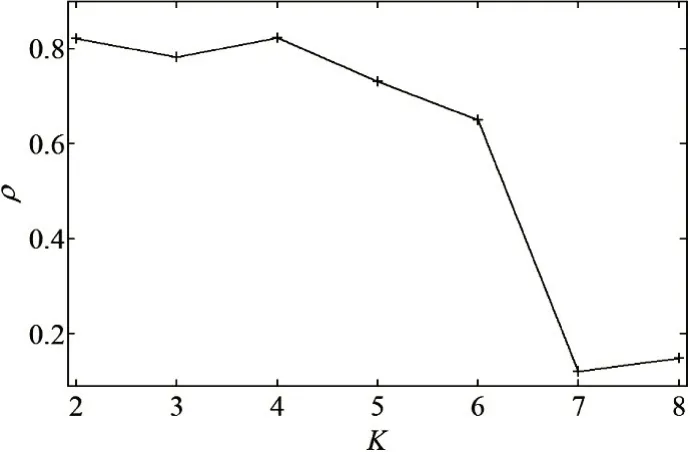
图3 不同K对应的互相关系数
接下来,分析模态个数K对VMD 滤波结果的影响。采用上述仿真信号,分别添加方差为0.8的均匀分布噪声和高斯白噪声。表1和表2分别给出了均匀分布白噪声和高斯白噪声时,不同模态个数K下单纯采用VMD方法的滤波结果的误差比较。从表1可以看出,对于包含了四个频率的时间序列,VMD中的互相关系数取最小值时的最优模态个数为K=7,此时滤波误差MAE 也取最小值。表2高斯白噪声的滤波结果与此类似。表1和表2的结果验证了基于互相关系数的模态个数估计模型的正确性。

表1 模态个数对滤波结果的影响(均匀分布噪声)

表2 模态个数对滤波结果的影响(高斯白噪声)
分别选取中值滤波、均值滤波、维纳滤波、EMD-维纳滤波与本文VMD-维纳滤波方法作比较。表3和表4分别给出了添加了均匀分布噪声和高斯白噪声后这几种方法的滤波结果,可看出,本文提出VMD-维纳滤波模型的去噪效果最佳,优于传统的维纳滤波以及EMD-维纳滤波方法,表明本文提出方法的性能。这是因为,基于互相关系数可以准确得到模态个数,改进VMD模型既消除了模态间的混叠并去除了原时间序列的高频噪声,同时实现了模态序列的平稳化;在此基础上采用维纳滤波,保证了滤波的效果。

表3 不同方法滤波性能比较(均匀分布噪声)

表4 不同方法滤波性能比较(高斯白噪声)
接下来以实测数据对去噪模型进行验证。实测数据为陕西省某区域区的电力负荷数据。首先采用VMD 方法进行分解,确定模态集合中的余量,然后计算不同模态个数K下的除余量后各分量负荷序列的互相关系数。图4为K取不同值时,余量序列与各模态分量之间的互相关系数,从中可以看出,不同K下得到的互相关系数均小于0.3,而当K取4时,余量和负荷模态重构后的互相关系数最小。因此,最优模态个数为4。

图4 不同K的模态分量的互相关系数
最后,将余量去除后的负荷序列进行重构,然后采用维纳滤波进行滤波得到滤波序列,经过VMD-维纳滤波后的负荷曲线较平滑,去除了原始实测序列中由于传感器附加的随机噪声干扰,有利于序列的后续建模分析。
5 结束语
提出了一种基于改进VMD 和维纳滤波的时间序列去噪方法,得到如下结论:
1)针对传统VMD模型存在的模态个数难以确定问题,基于余量序列与模态之间的互相关性确定最优模态个数,提升了时间序列模态分解的可靠性。
2)针对维纳滤波仅适合平稳信号的特点,首先采用VMD 分解,一方面消除了原始序列的非平稳性,同时降低了模态之间的频率混叠,并消除了原序列中的高频噪声;然后采用维纳滤波对各模态进行滤波,有效提升了去噪的性能。
最后需要指出的是,本文建立的去噪模型针对的是具有一定随机分布的白噪声。而实际中的时间序列可能还包括一些异常点(野值点),这些野值点也极大地影响序列分析的可靠性,下一步将改进方法以提高模型的适用性。

