船舶轴带无刷双馈电机并网滑模控制策略研究

刘春勇，高 岚

(武汉理工大学 能源与动力工程学院，湖北 武汉 430063)

无刷双馈电机(Brushless Doubly-Fed Generator，BDFG)具有双馈交流感应电机的优势，同时取消了电刷和集电环，作为船舶轴带发电机的应用前景值得期待[1]。船舶轴带发电系统并入主电网与柴油发电机共同为营运提供电力支撑，起到节能增效的作用；系统又能够吸收电网电能来驱动推进器，起到增强船舶生存能力的作用[2]。并网是轴带发电系统并入主电网稳态供电的起始点，并网时刻由于待并机与在网机之间差额电压引起的瞬态冲击电流不容忽视[3]。

针对BDFG的并网研究还不多见[4]。标量控制方案并网后，功率绕组输出端电压受电网电压钳位，无法实现电网电压跟踪控制[5]。通过在电网端与功率绕组输出端之间串联电抗器能够实现标量并网控制，但基于稳态模型的标量控制方案动态响应能力欠佳[6]。为获得较快的动态响应和简单的控制结构，采用直接转矩控制(DTC)同步并网控制方案[7]。Sadeghi等[8]提出基于简化电机模型的直接转矩并网控制，实现了并网平滑切换。DTC实现并网控制，开关频率不固定，转矩脉动无法避免。并网控制常采用矢量控制方案实现。高国章等[9]采用定子电压矢量控制保证输出电压幅值、频率的稳定，使用锁相环跟踪输出电压相位，实现并网控制，未进行并网过渡过程分析。但矢量控制在系统状态参数摄动和外界干扰时，难以得到理想的并网控制性能[10]。

滑模控制(Sliding Mode Control，SMC)处于滑动模态后对系统状态参数和外界扰动具有完全鲁棒性，具有快速控制、参数设计简单、易于实现等特点，在双馈电机并网控制中得到应用[11]。

本文借鉴双馈电机并网滑模控制方式，基于定子磁场定向机理，提出一种BDFG并网滑模控制策略。从BDFG运行原理入手，根据BDFG数学模型设计并网滑模控制器。利用MATLAB/Simulink平台进行参数摄动和外界扰动下仿真实验，并与传统PI控制性能对比，验证滑模并网控制系统的动态性能和鲁棒性。

1 BDFG运行原理与数学模型

1.1 BDFG运行原理

无刷双馈电机内部包含定子绕组和转子绕组(Rotor Winding，RW)，定子绕组上嵌有彼此独立、极对数不同的2套绕组，即功率绕组(Power Winding，PW)和控制绕组(Control Winding，CW)，BDFG发电系统结构框图如图1所示。PW通过断路器与电网相连，CW与变换器相连。PW侧变换器负责能量双向流动、单位功率因数控制、直流环节电容电压稳定，CW侧变换器为实现BDFG并网控制目标提供幅值、频率可调的交流励磁。

图1 BDFG发电系统结构框图

根据BDFG运行原理，可以得到电机驱动转速Nr与定子两套绕组频率关系:

fp=fc+Nr(pp+pc)/60，

(1)

式中，pp、pc分别为PW极对数、CW极对数；fp、fc分别为PW频率、CW频率。PW连接船舶工频电网，频率fp=50 Hz，定子两绕组极对数为定值，发电机驱动转速Nr与CW输入频率fc为变量。船舶在变工况下航行，主机转速改变会引起BDFG输出端频率发生改变，而船舶用电设备需要恒频交流电。因此控制器需要调节CW输入频率适应转速变化，实现BDFG变速恒频发电目标。

1.2 BDFG数学模型

首先建立定子磁场定向MT旋转坐标系下BDFG数学模型。PW侧电磁量采用发电机惯例，CW、RW侧电磁量采用电动机惯例[12]。

电压方程:

(2)

(3)

(4)

磁链方程：

(5)

(6)

(7)

式中,Ψ、i、u分别表示各定转子绕组磁链、电流、电压；下标M、T代表M-T坐标系下各电磁分量对应的M轴分量、T轴分量；下标s、p、c、r分别表示与定子绕组、PW、CW、RW相关的电磁量；s为微分算子；Rp、Rc、Rr分别表示PW相电阻、CW相电阻、RW相电阻；Lp、Lc、Lr、Mpr、Mcr分别为PW全自感、CW全自感、RW全自感、PW互感、CW互感；ωp、ωc、ωs分别为PW电角频率、CW电角频率、定子电角频率，三者之间关系为ωp-ppωr=ωc+pcωr=ωs,ωr为转子机械角频率。

电磁转矩Te方程：

Te=3ppMpr(ipTsipMr-ipMsipTr)/2-3pcMcr(icTsipMr-icMsipTr)/2。

(8)

机械运动方程表达式：

Jsωr=TL-Te-fωr，

(9)

式中，TL为柴油机输入机械转矩；J为转动惯量；f为摩擦因数。

2 BDFG空载并网滑模控制器设计

2.1 空载并网控制

空载并网控制实质是根据电网信息和发电机状态参数计算出满足并网条件的CW励磁，并通过CW侧变换器提供励磁，使电机输出端电压与电网电压始终保持相同的幅值、频率、相位。

并网前电机PW端未接入电网，处于空载运行状态，功率绕组电流分量为零。由于电机稳态时运行在工频条件下，电阻远小于电抗，忽略PW电阻。定子PW各电磁量空间关系如图2所示，取PW磁链Ψps与M轴相互重合，T轴在逆时针方向上超前M轴90°。在空间上，PW电压ups落后于PW磁链90°，即PW电压与PW磁链T轴负方向重合。d、q分别为旋转坐标系d轴、q轴，θp、θr分别为PW与静止坐标系α轴之间的转角、转子绕组与α轴之间的转角。

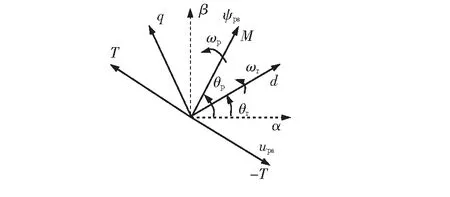
图2 定子PW各电磁量空间关系

结合式(2)～(7)，并省略RW电阻，化简得：

(10)

根据CW电压和磁链方程得：

(11)

式(10)、(11)构成基于定子磁链的并网矢量控制设计依据，可设计PI控制器。

2.2 滑模控制器设计

根据滑模控制思想进行滑模控制器设计。定义滑模超平面M轴分量和T轴分量：

(12)

式中，“*”为参考值。

对式(12)求导，并代入式(11)可得：

(13)

选定指数趋近律：

(14)

式中，k1、k2、k3、k4为滑模控制器参数，其值均大于0。

同时，采用饱和函数sat(s)代替开关函数sgn(s)进一步削弱抖振。结合式(13)、(14)得：

(15)

式中,由于计算复杂，定义4个变量分别为：

(16)

采用Lyapunov函数可以验证设计的滑模控制器具有渐进稳定性。根据以上分析，设计轴带BDFG空载并网滑模控制框图如图3所示。icabc、upabc、Udc分别为CW三相电流、PW三相电压、逆变器直流侧电压。

图3 轴带BDFG空载并网滑模控制框图

3 仿真分析

为验证滑模控制策略的有效性，在MATLAB/Simulink平台上搭建BDFG并网PI控制仿真模型、SMC仿真模型，并进行分析。BDFG参数(均已折算至PW侧)如表1所示，同步转速为500 r/min。电网相电压有效值为220 V，电网频率50 Hz。滑模控制器参数为k1=k3=1 500，k2=k4=5；PI控制器采用的参数为P=224，I=18 189。

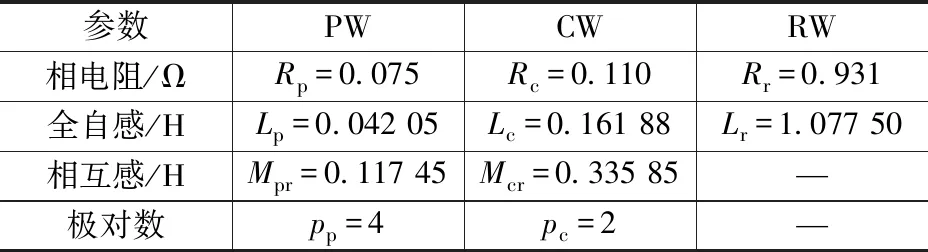
表1 BDFG参数

3.1 空载并网仿真

电机启动在亚同步转速400 r/min运行，在0.06 s时，转速突变至500 r/min，并网仿真波形如图4所示。

由图4知，SMC控制下启动，电机输出端电压与电网电压之间的差值逐渐变小，约0.3个周期(6 ms)趋近于零，而PI控制约1.5个周期(30 ms)趋于稳定状态。转速突变时，PI控制电压超调量为16%，电机输出端电压在SMC控制下与稳态时波形近似。可见，滑模控制改善了PI控制动态响应能力较差、超调量大的问题。

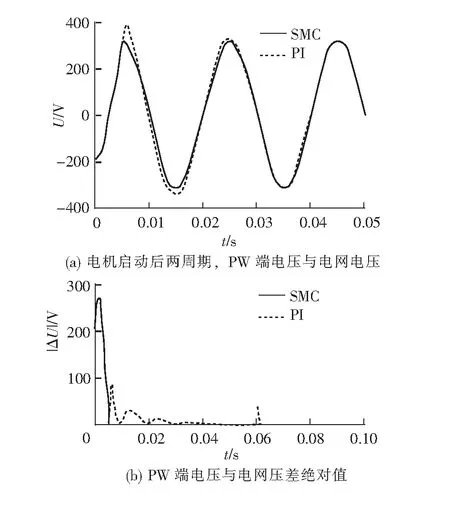
图4 SMC和PI并网控制仿真波形

3.2 电网电压波动仿真

船舶电网是孤网、小容量系统，大容量负载投入或切除易对船舶电网产生冲击，使电网电压波动。设定电网电压0.15 s时下降15%，并在0.2 s恢复至给定值，电网电压扰动下定子端电压响应波形如图5所示。

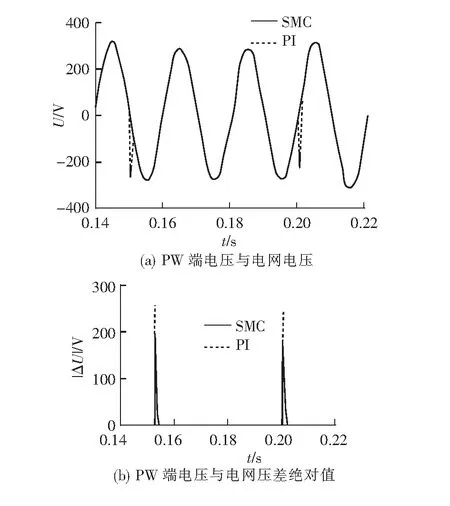
图5 电网电压扰动下，PW端电压响应波形

由图5知，电网电压波动时，PI控制、SMC均具有较好的动态响应时间，PI控制下的电压偏差约260 V。与PI控制相比，SMC下电机电压超调量下降22%。因此，SMC具有较好的电网电压跟踪性能。

3.3 电机参数摄动仿真

通过空载和堵转试验参数辨识得到的电机参数存在一定测量噪声。同时电机实际运行过程中，难免受内部磁场饱和影响导致电感值减小，环境温度升高导致绕组电阻增大。设置0.3 s时，电机转子电阻设定值增大50%，同时转子电感设定值减少3%，电机参数摄动时，定子端电压与电网电压差绝对值如图6所示。

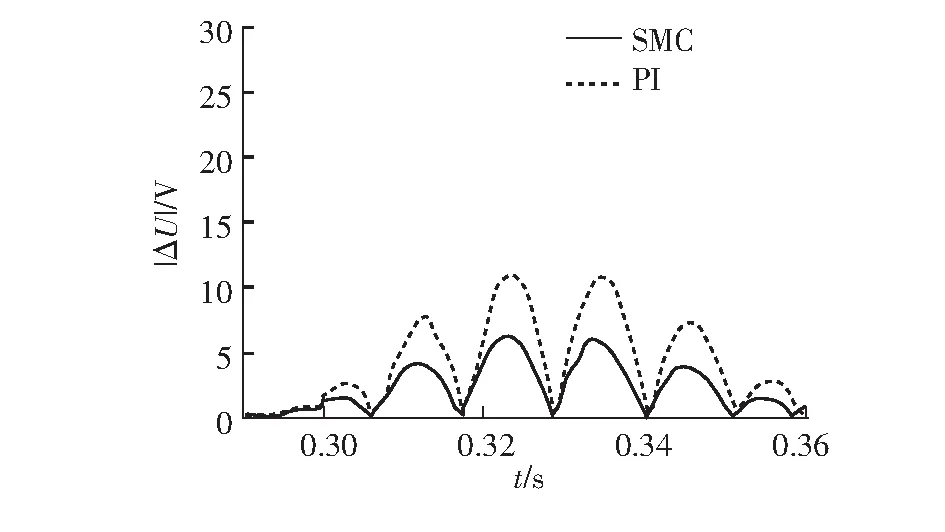
图6 电机参数摄动时定子端电压与电网电压差绝对值

由图6知，PI控制受电机参数摄动影响明显，稳态误差较大。SMC时电压稳态误差下降1.9%，保持了较好的电压跟踪性能，表明SMC在电机参数摄动时具有较好的鲁棒性。

3.4 系统并网过渡过程分析

仿真过程如下：电机稳定运行在400 r/min，满足并网条件，0.5 s启动并网，系统采用SMC并网时，功率绕组与转子绕组电流过渡过程如图7所示。ipa、ipb、ipc分别为功率绕组三相电流，ira、irb、irc分别为转子绕组三相电流，由图7可以看出，开关合闸后，PW电流波动幅值较小，未出现瞬态冲击电流，同时转子电流平滑过渡，实现了发电系统无瞬态冲击电流并网。

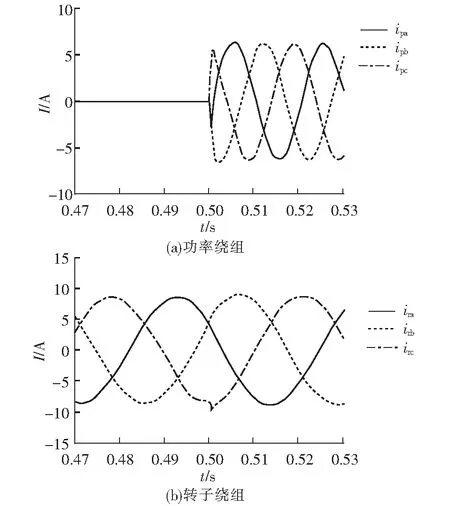
图7 SMC并网时，功率绕组与转子绕组电流过渡过程

4 结束语

为降低并网对船舶电网的影响，基于定子磁场定向原理提出船舶轴带BDFG空载并网滑模控制策略。实验结果表明：SMC能够在0.3个时钟周期跟踪电网电压，并网时稳态误差几乎为零，且未出现瞬态冲击电流，转子电流过渡平滑；与PI控制相比，电网电压扰动时电压超调量下降22%，电机参数摄动时电压稳态误差下降1.9%，具有较强的鲁棒性，提高了轴带发电系统的并网性能。