基于极限学习机的输配一体储能系统选址定容协同优化策略
郑 重,苗世洪,张松岩,姚福星,张 迪,韩 佶
(1. 华中科技大学电气与电子工程学院强电磁工程与新技术国家重点实验室,湖北 武汉 430074;2. 华中科技大学电气与电子工程学院电力安全与高效湖北省重点实验室,湖北 武汉 430074)
0 引言
近年来,全球环境气候问题突出,以风电、光伏为代表的新能源电站发展迅猛。由于风电、光伏等新能源发电方式具有随机性、波动性等强不确定性特征,其大规模接入将导致弃风弃光、潮流倒送、电网失稳等一系列问题日益严峻。在此背景下,储能系统凭借其自身所具有的调节灵活、响应迅速、安全可控等特性,逐渐引起社会各界的广泛关注。2020年3月11日,国家发改委印发《关于加快建立绿色生产和消费法规政策体系的意见》,在促进能源清洁发展方面指出,要加大对储能技术、多能互补的政策支持力度[1]。目前,储能技术正朝着转换高效化、高能量密度化和低应用成本化的方向发展。随着储能技术的研究和应用日渐成熟,储能系统的合理规划被公认为是促进清洁能源消纳、提高电网运行经济性和安全性的有效手段。
储能系统的有序接入是其技术经济性得以充分展现的重要前提。针对配电网储能选址定容问题,国内外学者已经开展了大量相关研究。文献[2]提出了一种多能互补发电系统中分布式电源与广义储能的双层优化规划方法。文献[3]提出了一种考虑源网荷灵活性资源的配电网储能优化配置方法,并采用内嵌潮流计算的多目标复合差分进化算法进行求解。文献[4]以储能系统荷电状态为参量,提出了基于可变功率修正系数的储能系统充放电控制策略,并以此为基础构建了计及风电场投资、运行成本和储能运行寿命的储能容量优化模型。文献[5]综合考虑火电煤耗运行成本、风电弃风功率、储能建设成本等优化目标,提出了一种计及风险备用约束和多能源机组组合调度约束的输电网风储联合配置的规划方法。文献[6]计及设备投资、储能运行、风电消纳等约束,建立了涵盖规划决策、运行评估的输电网风储两阶段联合规划模型。上述文献主要研究了储能电站在输电网和主动配电网背景下的选址定容优化问题,未充分计及输电网和配电网间存在的协同关系,电网整体资源利用不充分,存在一定局限性。
随着智能电网的不断发展,输电网与配电网间信息数据耦合不断增强,输配电网协调优化必要性日益彰显[7-9]。现有输配协同优化方法主要可以分为集中式和分布式2 类。其中,传统集中式算法将输配电网视为统一整体,以系统整体经济性最优为目标进行计算;传统分布式算法将输配协同优化问题分解为输电网及配电网优化子问题,并利用节点边际电价LMP(Locational Marginal Price)和购电功率等边界观测量反复迭代,进而实现输配电网信息协同。文献[10]提出了一种基于LMP 和配电网联络线购电功率交互的输配电网协调优化算法——异构分解HGD(HeteroGeneous Decomposition)算法,计及电网直流潮流约束,将输配一体经济调度问题分解为输电网经济调度和配电网经济调度2 个子问题,并通过迭代获取模型最优解。文献[11]在传统HGD 算法的基础上,通过数值拟合求解LMP 对负荷的灵敏度,提升传统HGD 算法收敛性。与此同时,鉴于传统分布式优化算法具有需要反复迭代、计算时间较长的问题,文献[12]提出了一种非迭代解耦的协调求解方法,通过网损修正提升算法精度,相较于传统分布式算法计算效率得以提升。文献[13]提出了一种基于改进广义Benders 分解的输配电网协调经济调度方法,并利用预定可行割集的方式减少迭代次数。综上所述,现有部分输配一体优化算法采用直流潮流模型,由于输配电网有功无功无法解耦,该方式下的计算精度难以得到保证。此外,现有输配一体优化算法研究主要集中在调度层面,设计输配一体协同的储能选址定容算法较少涉及。与此同时,目前关于输配一体协同优化核心是通过输电网与配电网间反复交互迭代获取全局最优解。当网络规模扩大时,输电网优化及配电网子问题计算次数将进一步增加,算法收敛性面临严峻挑战。
针对以上问题,本文提出了一种基于极限学习机ELM(Extreme Learning Machine)的输配一体储能系统选址定容协同优化策略。首先,以电网经济性最优为目标,计及电网安全稳定约束及联络线功率约束,建立基于二阶锥松弛的输配一体储能选址定容模型。其次,推导包含二阶锥约束的输电网节点边际电价TLMP(Transmission Locational Marginal Price),并通过ELM 分别构建输电网及配电网储能选址定容状态表征模型,实现输、配电网子优化问题的快速响应。然后,以TLMP 和配电网需求功率为交互变量,提出基于ELM 的输配一体储能系统选址定容优化算法,以获取储能系统全局最佳安装位置及容量。最后,通过算例分析验证了本文所提算法的有效性及鲁棒性。
1 输配一体储能选址定容优化模型
随着智能配电网、主动配电网建设的不断推进,输配电网数据信息大量交互、深度耦合,输电网向配电网提供电能支撑,配电网潮流分布亦对输电网存在一定制约,传统优化算法将配电网“被动地”视为输电网的固定负荷节点,无法获取系统全局最优解,适应性和可移植性亦较差,显然已不再适用。鉴于此,本文首先建立输电网及配电网储能选址定容模型,并进一步利用二阶锥松弛对模型非凸约束进行转化,建立输配一体储能选址定容优化模型,为后续算法的提出奠定基础。
1.1 输电网储能选址定容优化模型
1.1.1 目标函数
输电网储能选址定容模型以系统发电成本Ftrans,gen、网损成本Ftrans,loss、储能设备投建等年值Ftrans,invest、火电机组启停成本Ftrans,shut和弃风弃光成本Ftrans,abandon最小为优化目标,具体表达式如下:
1.1.2 约束条件
1)功率平衡约束。
输电网运行时应考虑如下系统有功及无功平衡约束:



式中:Ti,on、Ti,off分别为机组i持续运行时间和持续停运时间;Ti,on,min、Ti,off,min分别为机组i最小持续运行时间和最小持续停运时间。
1.2 配电网储能选址定容优化模型
1.2.1 目标函数
配电网储能选址定容优化模型以购电成本、网损成本、弃风弃光成本和储能设备投建等年值之和最小为优化目标,具体表达式如下:

1.2.2 约束条件
配电网功率平衡约束、潮流约束等约束表达形式及变量定义与输电网对应约束(式(8)—(15))类似,具体见附录A。
1.3 基于二阶锥松弛的输配一体电网储能选址定容优化模型
1.3.1 基于二阶锥松弛的模型非凸约束转化
由上述分析可知,本文所建立的输电网储能选址定容模型和配电网选址定容模型中均包含潮流约束等典型非凸约束,如式(8)所示。考虑到目前非凸优化问题无法使用成熟商业软件进行求解,同时启发式算法在求解非凸优化问题时存在全局搜索能力差、精度低等缺陷[2],因此本文引入二阶锥松弛技术[15],将输电网及配电网储能选址定容非凸优化问题转换为凸优化问题,从而降低模型求解难度。以输电网储能选址定容模型为例,介绍该模型的二阶锥松弛过程。首先定义变量如下:

式中:Ft-d为输配电网总体经济性优化目标;ND为配电网总数量。
值得说明的是,本文以1个输电网与k个配电网组成的系统为例进行分析,类似地,本文所提模型与算法能够自然地推广至m个输电网与k个配电网所组成的系统。
输配一体电网储能选址定容优化模型约束即为输电网储能选址定容模型与配电网储能选址定容模型约束的并集。
综上,本文所建立的输配一体储能选址定容模型如下:
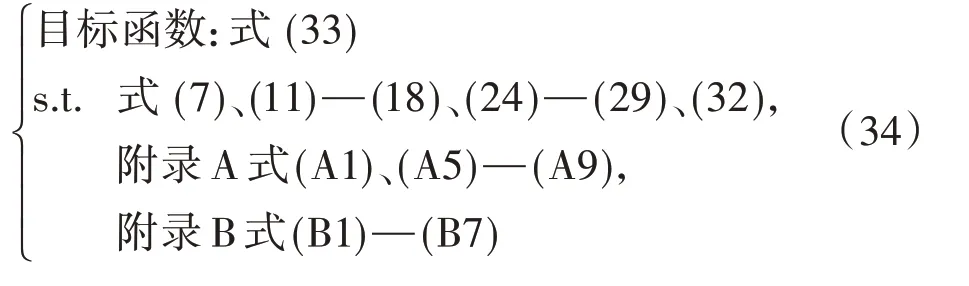
2 基于ELM 的输配一体储能选址定容模型求解
在建立输配一体储能选址定容模型后,由于传统输配一体优化算法存在计算时间长、收敛困难、全局搜索能力差等缺陷,本文进一步提出基于ELM 的输配一体储能选址定容算法,从而改善算法计算时间及收敛性。
2.1 包含二阶锥约束的输配电网LMP推导
TLMP 和配电网购电功率是表征输配电网协同运行机制的重要指标,能够充分反映输配协同过程中输电网优化信息。TLMP 定义为满足输电网节点新增单位负荷的系统边际成本[16]。在输配电网协同优化领域,TLMP 具有反映输电网电能生产成本、引导配电网购电计划制定、促进输配协同优化问题收敛至全局最优解等重要作用。目前,部分学者在研究输配一体优化问题时采用出清电价或以直流潮流为基础的电网LMP[17-18],该方法虽然计算简单,但无法充分表征电力供需关系。与此同时,传统TLMP求解方法亦无法解决模型二阶锥约束所导致互补松弛条件出现二次项的问题,以输电网二阶锥约束为例,式(32)对应的互补松弛条件为:

式中:λcone为式(32)所对应的拉格朗日乘子。
由于式(35)为二次项形式,因此传统方法将难以直接获取对应TLMP,从而极大地增加了模型求解复杂度。鉴于此,在基于二阶锥松弛的输配一体电网储能选址定容优化模型的基础上,本文进一步推导含二阶锥约束的TLMP 表达式。首先,对二阶锥约束的互补松弛条件形式进行等价变形。以输电网二阶锥约束为例,式(35)所示的互补松弛条件可表示为:

至此,本文完成了含二阶锥约束的输配一体储能选址定容模型TLMP 推导,为输配电网交互关系的有效表征提供理论基础。
2.2 基于ELM的输配电网状态表征模型
由上述分析可知,传统输配一体协调优化算法通常需要反复迭代求解输电网子优化及配电网子优化问题,随着迭代次数的提升,算法的时间复杂度和空间复杂度主要来源于输配电网子优化问题;此外,电压等级的升高、网络拓扑的复杂化均将导致算法的计算时间、计算精度和收敛性受到极大挑战。鉴于此,本文提出一种基于ELM 的输配电网储能选址定容状态表征模型。ELM是一种新型单隐层前向神经网络。与传统智能算法相比,ELM 训练过程中不需要调整网络的输入权值以及隐元的偏置,能够产生唯一的最优解,因此具有学习速度快且泛化性能好的优点[19]。
应用研究成果表现为建立拥有自主知识产权的PKPM系列绿色建筑规划设计软件集成系统:包括场地优化设计软件、居住区规划软件、日照设计软件、园林设计软件、能耗计算软件、节能设计软件、能效测评软件、自然采光软件、室内自然通风设计计算软件和绿色建筑评价软件,如图2~图11所示。
ELM的输入矩阵和输出矩阵可分别表示为:
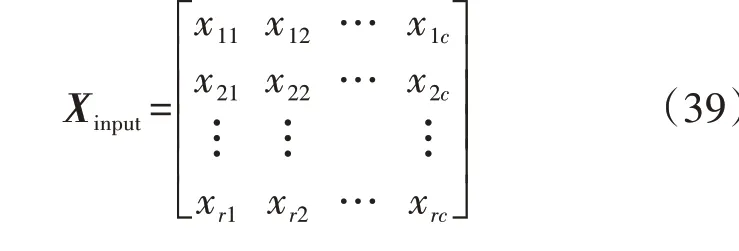

式中:Xinput、Youtput分别为ELM 输入矩阵和输出矩阵;c为ELM 训练样本数量;r为输入向量维度;s为输出向量维度。
进一步地,假设输入层S与隐层B连接权值矩阵W和隐层B与输出层F连接权值矩阵β分别为:

式中:G(·)为ELM 网络的隐层传输矩阵;wi·=[wi1,wi2,…,wir](i=1,2,…,l)为连接权值矩阵W的第i个行向量;x·j=[x1j,x2j,…,xrj]T(j=1,2,…,c)为输入矩阵Xinput的第j个列向量。
由于输配一体储能选址定容模型中数据量冗杂,输配电网间高度耦合,因此对于输电网和配电网选址定容模型而言,确定系统控制变量、状态变量是实现ELM 迅速表征的首要前提。针对本文所研究的输配电网储能选址定容问题,需要分别训练2 类ELM,即输电网状态表征模型及配电网状态表征模型,分别对应输电网及配电网储能选址定容子优化问题。其中,输电网控制变量、状态变量分别设置如下:


式中:Xtrans,input、Ytrans,output、Xdis,k,input、Ydis,k,output分别为输电网ELM 训练输入矩阵、输电网ELM 训练输出矩阵、第k个配电网ELM 训练输入矩阵和第k个配电网ELM训练输出矩阵。
综上,本文进一步构建基于ELM 的输电网状态表征模型及配电网状态表征模型,具体流程如下。
步骤1:分别确定输电网和配电网控制及状态向量[Xtrans,control,Ytrans,state]、[Xdis,k,control,Ydis,k,state]。
步骤2:数据输入。分别以输电网和配电网为研究对象,初始化输入层S和隐层B连接权值矩阵Wtrans、Wdis,k以及隐层神经元的阈值btrans、bdis,k。
步骤3:确定隐层神经元激活函数,本文选择sign函数作为隐层神经元激活函数。
步骤4:依次计算输电网及配电网隐层输出矩阵Gtrans(·)、Gdis,k(·)及输出层权值矩阵βtrans、βdis,k,并最终根据式(39)—(45),分别构建输电网状态表征模型和配电网状态表征模型。
2.3 基于ELM的输配一体储能选址定容算法
2.3.1 算法流程
在2.1 节和2.2 节的研究基础上,本文进一步提出基于ELM 的输配一体储能选址定容算法。该算法将TLMP 和配电网购电功率作为交互变量,通过基于ELM 的输配电网状态表征模型实现输电网及配电网储能选址定容子问题求解,并构造算法收敛判据,迭代求解直至算法收敛后输出系统储能选址定容优化结果。算法流程图如附录D图D1所示。
2.3.2 算法最优性验证
下面本文将进一步对算法的最优性进行证明。由附录D图D1可知,本文所提出的基于ELM的输配一体储能选址定容算法收敛判据为:



综上,本文提出的基于ELM 的输配一体储能选址定容算法能够充分计及输配电网状态交互,同时利用ELM 的快速响应特性,克服了传统算法在计算时间和收敛性方面的缺陷,算法的最优性亦得到有效证明,具有优秀的应用价值。
3 算例分析
本文算例采用如图1 所示的T6D7D9 系统进行分析,该系统包含1个输电网及与之相连的2个配电网。系统基本参数见文献[20],本文以锂电池储能为例开展算例分析,储能系统参数见文献[21],输配电网网架参数及锂电池基础参数见附录E 表E1—E4。在本文算例中,仅考虑配电网向输电网购电,不允许配电网潮流返送。
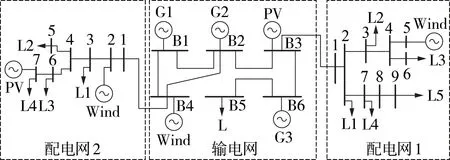
图1 算例系统结构图Fig.1 Structure diagram of example system
本文分别从计算精度、鲁棒性及算法有效性等多个维度进行深入探讨,具体结果如下。
3.1 状态表征模型精度验证
为验证本文所提出的基于ELM 的输配电网状态表征模型的计算精度,在本文算例中,利用输电网及配电网选址定容子优化程序得到600 组数据,选取其中的50%作为训练数据,剩余的50%作为测试数据,输电网及配电网1、配电网2 的300 组测试样本对应的训练误差如图2所示。

图2 ELM训练误差Fig.2 Training errors of ELM
由图2 可知,输电网、配电网1 和配电网2 的ELM平均训练误差分别为-0.15%、-2.60%和-2.25%,输电网、配电网1 和配电网2 的ELM 绝对训练误差分别为0.52%,2.82%和2.68%,系统ELM 绝对训练误差为2.05%。可见ELM 训练误差基本控制在±2%误差带以内,最大训练误差控制在10%以内,ELM 的训练精度得以有效验证。因此,本文所提出的基于ELM 的输电网及配电网状态表征模型能够有效反映输电网与配电网变量之间的耦合关系,在确保输电网和配电网储能选址定容优化模型求解精度的前提下,降低了模型计算复杂度,提升了模型收敛速度。
3.2 算法对比
HGD 算法是一种较为经典的输配电网交叉迭代算法[10],广泛应用于输配电网协调优化调度、控制等领域。本文将基于ELM 的输配一体储能选址定容算法与传统集中式算法和基于HGD 的分布式算法(简称HGD 算法)进行对比,由于基于直流潮流的HGD 算法计算误差较大,精度较低,不具有代表性,因此本文选取基于交流潮流的HGD 算法和集中式算法与本文算法进行对比,分别构建了以下3 种场景:场景1,输配电网协同进行储能选址定容,利用本文所提出的基于ELM 的输配一体储能选址定容算法进行优化,进而获取储能选址定容结果;场景2,利用HGD 算法获取储能选址定容结果;场景3,利用集中式算法获取储能选址定容结果。
场景1—3下的结果对比如表1所示。
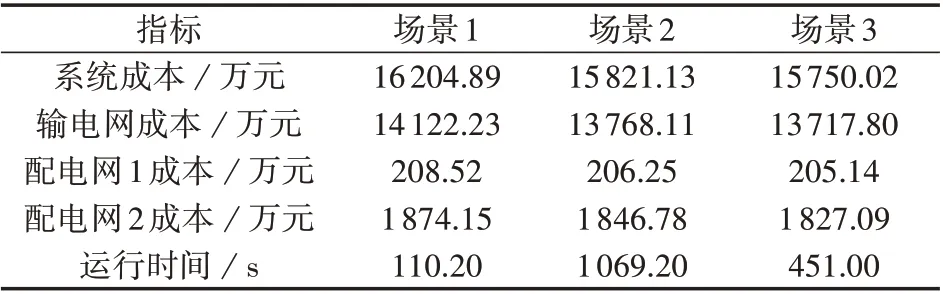
表1 3种场景的算法对比Table 1 Comparison of algorithms among three scenarios
由表1 可知,本文所提出的基于ELM 的输配一体储能选址定容算法与传统集中式算法和HGD 算法求解结果基本保持一致,3 种算法的输配电网优化目标求解误差控制在3%以内。与此同时,由于本文算法利用ELM 的构造输配电网状态表征模型替代了HGD 算法的输配电网子程序优化过程,在输、配电网独立优化过程中节省了大量时间,因此本文算法在计算效率方面相较于传统集中式算法和HGD算法优势更显著。
3.3 算法初值敏感性分析
算法的初值敏感性是衡量输配一体选址定容算法收敛稳定性的重要依据之一。由上述分析可知,本文算法在初始化过程中首先需要给定TLMP,进而通过迭代获取模型最优解。而部分传统分布式优化算法求解结果受初值影响较为严重,为研究TLMP初值是否将对算法最终结果及收敛性产生显著影响,本文进一步针对所提算法的初值敏感性开展算例分析,分别构建以下3 种场景:场景4,在场景1 的基础上增加[0,10%]Llmp随机误差;场景5,在场景1的基础上增加[-10%,0]Llmp随机误差;场景6,在场景1的基础上增加[0,20%]Llmp随机误差;场景7,在场景1的基础上增加[-20%,0]Llmp随机误差。
分别对场景4—7 进行优化求解,场景1 与场景4—7求解结果对比如表2所示。

表2 算法初值敏感性分析Table 2 Sensitivity analysis of algorithm initial value
由表2可知,场景1与场景4—7相比,最大计算误差为0.07%,即本文所提出的基于ELM 的输配一体储能选址定容算法针对不同计算初值的最终计算结果误差均保持在0.1%以内,相较于传统分布式算法,本文算法所具备的良好的鲁棒性及适应性得以充分体现。
3.4 输配一体与输配分离场景对比
为进一步体现本文所提出的输配一体储能选址定容算法在资源协同方面的优势,本文针对输配分离场景及输配协同场景开展算例分析,构建输配分离场景如下:场景8,输电网及配电网分离进行储能选址定容。在此场景下,配电网视为输电网侧固定负荷节点,首先初始化TLMP,并依次进行配电网优化及输电网优化,输配电网在选址定容过程中无交互迭代过程。
场景1 与场景8 的对比结果如表3—5 所示,配电网购电量、输配电网储能系统全时段出力等结果见附录F图F1—F5。
由表3 可知,场景1 相较于场景8 而言,系统总经济成本下降了717.73万元,其中,输电网总经济成本下降了632.77 万元,配电网1 总经济成本下降了58.37 万元,配电网2 总经济成本下降了26.58 万元,系统中各主体经济性均得到不同程度的改善。与此同时,输配一体储能选址定容场景能够显著降低网络损耗,相较于场景8,场景1 的输电网网损下降了19934.73 MW·h,配电网网损下降了1505.24 MW·h;此外,在场景8 中配电网2 新能源弃电量增加了3 723 MW·h,清洁能源消纳问题进一步凸显。
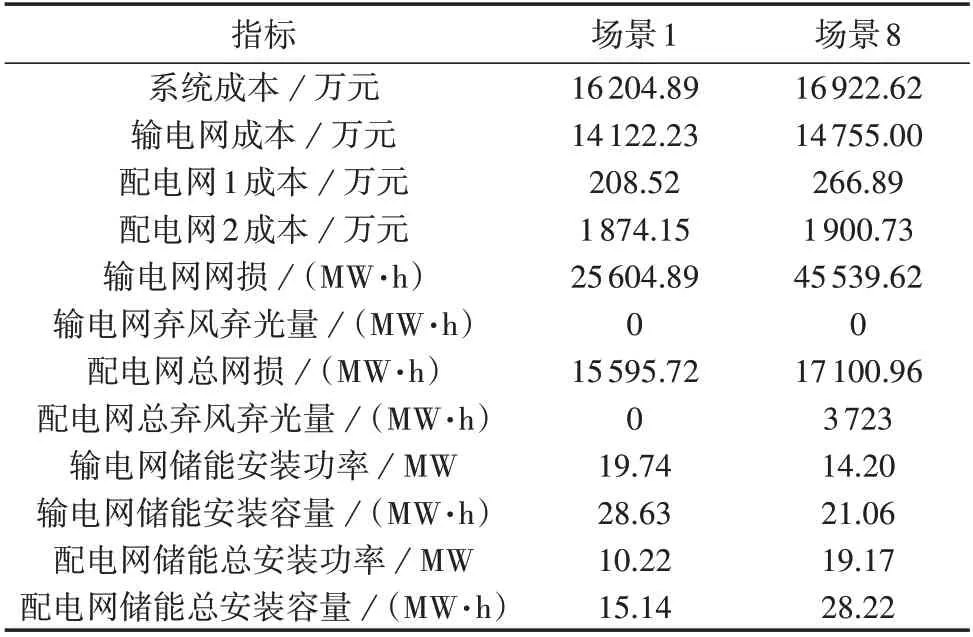
表3 场景1与场景8对比结果Table 3 Comparison of results between Scenario 1 and Scenario 8

表5 场景8储能选址定容方案Table 5 Energy storage location and capacity determination scheme of Scenario 8
通过对比附录F 图F1—F5 可知,TLMP 能够充分表征输电网优化信息并将其传递至配电网,配电网将根据不同典型日时段下的TLMP,主动调节自身运行状态,并通过购电功率需求的方式反馈配电网优化信息,最终达到三者的利益均衡。场景8 中配电网与输电网资源缺乏有效协同,因此相较于场景1,场景8 中配电网1、配电网2 均需要投建更多储能系统,以满足自身运行经济性需求,故而造成显著的投资冗余;此外,为了提升输电网及配电网自身运行经济性,场景8 中储能系统需要反复充放电进行调节,全网资源缺乏有效协同。因此,计及输配协同的储能选址定容场景能够充分考虑输配电网潮流耦合关系,从系统整体角度确定电网储能系统最优安装位置及对应安装容量,实现系统全局优化。
综上,相较于输配分离储能选址定容场景,输配一体储能选址定容场景能够更加充分地调用全网资源,通过状态变量所反映的信息主动调节输电网及配电网运行状态,合理调控全网储能系统资源,从而实现降低系统网损,促进清洁能源消纳,提升系统经济性的目标。
3.5 大规模网络算例分析
为验证本文所提算法在大规模算例网络中的优势,进一步针对T118D33D33 网络开展算例分析,系统算例结构图见附录G图G1。
选取本文算法、HGD 算法和集中式算法进行对比分析,结果如表6所示。

表6 3种算法结果对比Table 6 Comparison of results among three algorithms
由表6 可知,在计及输配电网交流潮流的T118D33D33 算例系统中,由于计算规模较大,采用传统集中式优化算法已经出现了计算无法收敛的情况,同时相较于传统HGD 算法,本文算法能够在确保输电网及各配电网计算误差小于2%的情况下,计算时间缩短了98.06%,求解效率提升效果显著。
值得说明的是,受气候、地形等自然因素的影响,风电及光伏机组出力具有间歇性、波动性、随机性等特点。为研究风光不确定性对本文模型及算法的影响,本文进一步构造风光不确定性场景并开展算例分析,其结果见附录H。
随着输配电网规模的不断增大,模型决策变量与约束条件亦将增加,本文算法在收敛性和计算速度方面的优势将得以进一步凸显。
4 结论
本文以输配电网整体经济性最优为目标,计及输配电网安全稳定运行约束,构建了基于二阶锥松弛的输配一体电网储能选址定容优化模型,并同时提出了一种高效、准确的输配一体储能系统选址定容优化策略,最终通过算例仿真得出以下结论。
1)相较于输配分离储能选址定容场景,本文所建立的输配协同储能选址定容场景中系统总经济成本下降了717.73 万元,系统总网损下降了21439.97 MW·h,新能源消纳量提升了3723 MW·h。因此,本文所建立的基于二阶锥松弛的输配一体储能选址定容模型,能合理利用系统可调控资源,有效促进清洁能源安全消纳,降低网络损耗,提升输电网及各配电网经济性,实现“互利共赢”的目标。
2)相较于传统集中式及分布式算法,本文所提出的基于ELM 的输配一体储能选址定容算法能将计算时间缩短75%以上。因此,本文所提算法能够在确保算法计算精度的前提下,显著降低计算复杂度,提升算法收敛性,实现输配电网储能系统的全局最优配置。
输配协同储能选址定容优化问题本质上是一个高维非凸优化问题,求解复杂,收敛性难以保证。在确保输配电网计算精度的前提下,进一步提升本文所提模型及算法在复杂场景下的鲁棒性和收敛性,是需要进一步研究的问题。与此同时,随着系统网络规模的进一步扩大,本文所提模型及算法将拥有更加广阔的应用前景。
附录见本刊网络版(http://www.epae.cn)。

