基于改进KDE法和GA-SVM的多风电场聚合后输出功率长期波动特性预测方法

肖 白，邢世亨，王茂春，杨森林，苟晓侃

（1. 东北电力大学电气工程学院，吉林 吉林 132012；2. 国网吉林省电力有限公司延边供电公司，吉林 延吉 133000；3. 国网青海省电力公司，青海 西宁 810008）

0 引言

为应对传统化石资源枯竭和环境污染等问题，我国大力开发利用风能资源。然而风的随机性和不确定性使得大规模风电并网给电力系统规划与运行带来不利影响［1］。正确分析、把握和利用风电功率波动特性是实现含风电电力系统优化规划、调度和控制的基础［2-4］。

风电功率波动特性就是对风电输出功率波动在单位时间内变化情况的描述与刻画。对不同时段内风电功率波动特性的研究对应于处理含风电电力系统中不同方面的问题。考虑到电力系统规划工作通常是以年为单位的，需要把握未来某年内的风电功率波动特性，而电力系统日前调度和实时控制工作通常是以天和分钟为单位的，需要把握未来一天或几分钟内的风电功率波动特性，因此本文将前者称为长期波动特性，将后者称为短期波动特性。

未来的风电功率波动特性是未知的，通常需采取预测手段。预测过程中涉及采样时间尺度的问题，即数据的采样间隔选取问题，目前常用的采样间隔为5 min、15 min、1 h 和1 a。由于风电功率波动特性分析的单位时间不同于风电功率预测中的采样时间尺度和预测周期，但它们之间又有匹配关系，因此研究规划目标年的风电功率长期波动特性不但具有重要的理论意义，而且对于解决大规模风电并网导致的电力系统规划难题具有重大的工程实用价值。

目前针对风电功率长期波动特性的研究较少。文献［5］提出一种基于利用持续功率曲线刻画风电功率长期波动特性的风电场群功率汇聚外送输电容量的静态优化方法；文献［6］构建考虑相关性的光伏电站群等值功率模型，同样在利用其持续功率曲线刻画光伏功率长期波动特性的基础上，建立一种光伏电站群外送输电容量的优化配置方法；文献［7］利用持续功率曲线建立风电与光热、风电与光伏联合外送容量配置模型。上述研究都是直接将历史风电或光伏输出功率长期波动特性在未来场景下进行应用，而没有考虑和处理未来场景下风电或光伏发电装机容量的增长导致输出功率长期波动特性改变的问题。

目前针对风电功率短期波动特性的研究较多。文献［8-9］定量分析风电功率波动在不同时间、空间尺度下的分布特性；文献［10-11］对大规模风电功率波动规律进行研究，分析多风电场间和风电机组间的平滑效应。在风电功率预测方面的方法较多且研究主要针对恒定装机容量下的风电短期或超短期时序特性。文献［12-14］采用隐马尔科夫链、马尔科夫链蒙特卡洛MCMC（Markov Chain Monte Carlo）法和自回归滑动平均模型ARMA（AutoRegressive Moving Average model）等方法建立多风电场的输出功率时间序列预测模型。然而，由于在含大规模风电的电力系统规划中，规划目标年的风电装机容量由当前年的风电装机容量和待建风电场的装机容量构成，在当前年不可能有新增装机输出功率的历史数据，因此无法直接套用现有的风电功率预测方法和风电功率短期波动特性的分析方法。

考虑到规划目标年与当前年的风电装机容量不同，风电功率波动特性受到装机容量的影响，需要对规划期内某一规划目标年的风电功率长期波动特性进行预测。文献［15］利用风电实测数据模拟风电场群的汇聚过程，建立风电场群持续功率的汇聚演变模型，为获取规划目标年的风电场群输出功率长期波动特性提供了思路，但其精度有待进一步提高。

针对上述问题，本文首先对风电功率长期波动特性的刻画方式进行分析并选择最佳的表征方法；其次利用改进核密度估计KDE（Kernel Density Es⁃timation）法和基于遗传算法GA（Genetic Algorithm）寻优的支持向量机SVM（Support Vector Machine）（简称GA-SVM）构建多风电场在各聚合阶段的输出功率概率密度演变预测模型；然后对预测结果进行反演得到规划目标年含待建风电场的多风电场聚合后的持续功率曲线；最后通过工程实例分析证明本文方法的正确性和有效性。

1 风电功率长期波动特性预测方法基本原理

本文提出一种基于改进KDE法和GA-SVM预测多风电场聚合后输出功率长期波动特性的方法。

首先，基于在役风电场实测运行数据，综合考虑时序功率曲线、持续功率曲线和数理统计方法，确定风电功率长期波动特性的最佳表征与刻画方式，并揭示多风电场聚合过程中风电功率随装机容量增大的变化规律。

其次，运用改进KDE 法计算含多风电场所有可能聚合过程中各装机容量下的输出功率概率密度分布。

然后，结合规划目标年风电场装机容量信息，建立基于SVM 的多风电场聚合后规划目标年输出功率概率密度的演变预测模型，其中在优化SVM 参数的过程中采用GA进行寻优。

最后，根据多风电场聚合后输出功率的概率分布与持续功率曲线的对应关系，反演出与规划目标年输出功率概率密度相对应的持续功率曲线，并用其表征多风电场聚合后的规划目标年输出功率长期波动特性。

2 风电功率长期波动特性的刻画

2.1 风电功率长期波动特性的表征方法分析

时序功率曲线可以直观地反映各时刻的风电功率情况，通过计算其差分值来刻画风电功率的短期波动特性，是实现电力系统优化控制和调度的基础，但其无法直观地反映风电场群在一段时间内的输出电量大小和输出功率最大值。

持续功率曲线可以直观地反映发电利用小时数、发电量、风电保证容量、风电功率上限和最大发电小时数等特征指标，便于刻画风电功率的长期波动特性，是对含大规模风电电力系统进行规划的重要工具。基于在役风电场实测运行数据，图1 给出了用于描述风电功率长期波动特性的年持续功率曲线。图中，横坐标为年持续时间，纵坐标输出功率为以装机容量为基准的标幺值（后同），曲线表示风电输出功率波动特性情况。曲线上点A—D分别表示一年中风电输出功率最大值、输出功率上限值、保证输出功率值和输出功率最小值。根据选择的置信度不同，点B、C的位置会发生变化。E为曲线与坐标轴围成的面积，表示风电等效年满发利用小时数，根据曲线也较易推得风电的年发电量和容量系数等指标。

图1 风电的年持续功率曲线Fig.1 Annual duration power curve of wind power

数理统计法通过计算风电功率的概率分布以及方差、最大值、最小值、差分量等统计量来刻画风电功率的波动特性，而且易于得到风电功率波动特性的量化值，但是由于在制定电力系统规划方案的过程中，需要用到风电输出功率的幅值大小及一定时间内的电量大小来处理电力电量平衡的问题，因此基于数理统计法得到的风电功率波动特性量化值不便于直接用于电力系统规划。

由于准确刻画风电功率概率分布有利于掌握风电功率长期波动情况，因此本文基于在役风电场实测运行数据给出某风电场输出功率概率密度曲线，如图2 所示。由图可知，该风电场的输出功率具有低输出功率部分的概率密度高、高输出功率部分的概率密度低的特点。

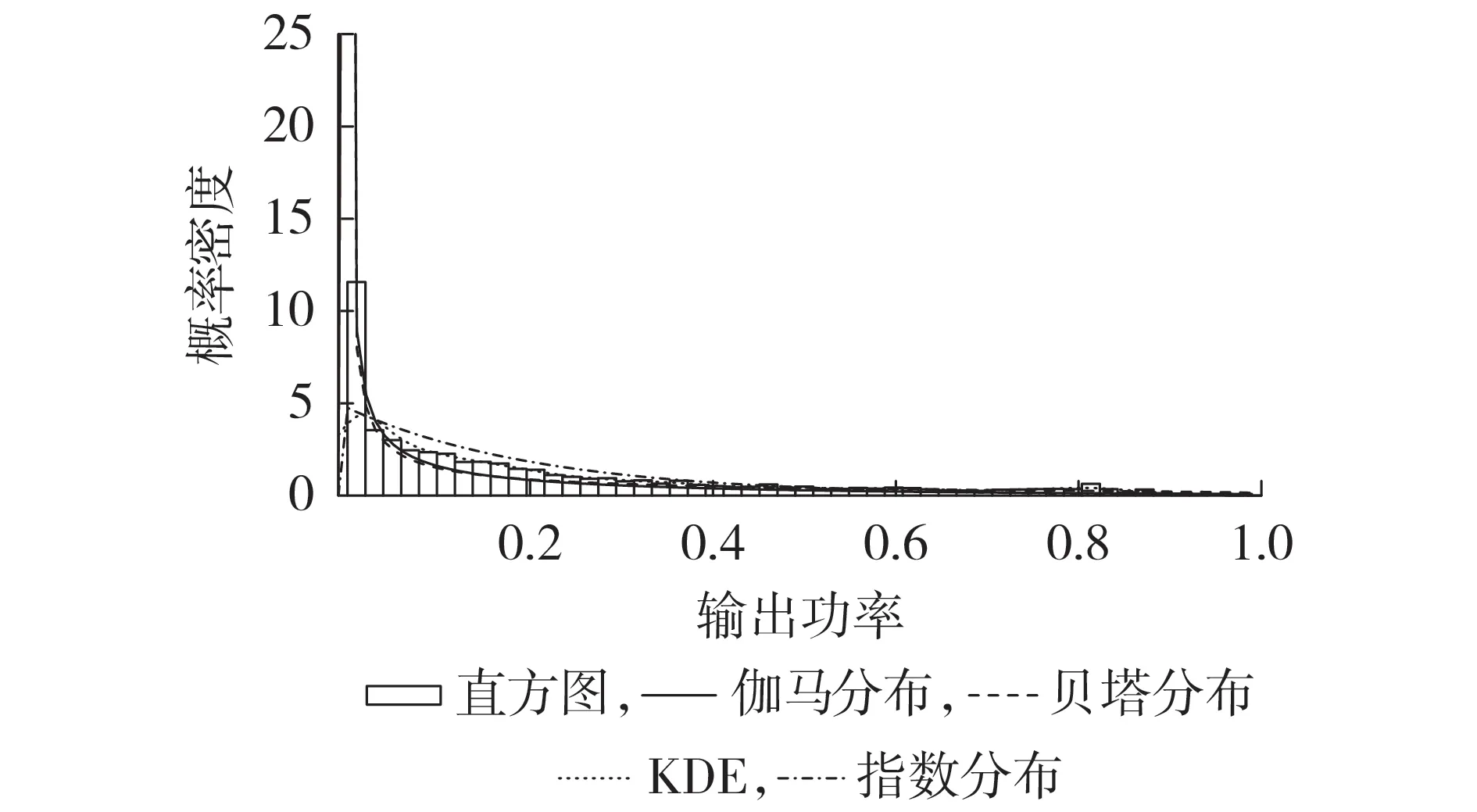
图2 风电功率概率密度曲线Fig.2 Probability density curves of wind power

综上，本文采取将数理统计法中的概率分布和持续功率曲线相结合的手段来研究含大规模风电电力系统规划中如何表征和刻画风电功率长期波动特性的问题。

2.2 多风电场聚合过程中装机容量与风电功率的随动变化关系

由于各风电场的地理位置和装机容量不同以及风资源的时空差异性，多风电场聚合过程中不同阶段都会呈现不同的输出功率波动特性。若采用持续功率曲线法来描述多风电场聚合过程中风电功率随着装机容量增大而表现出的变化规律，则可用式（1）表示。

式中：i=1，2，…，I为多风电场聚合过程中的阶段数，I为聚合阶段总数；j=1，2，…，J为第i个聚合阶段参与聚合的风电场数量，J为风电场总数；Fi，j为第i个聚合阶段共计j座风电场聚合后从装机容量到风电持续功率向量的映射；Si，jN为第i个聚合阶段共计j座风电场聚合后的总装机容量；Pi，j=[Pi，j1，Pi，j2，…，Pi，j Z]T为第i个聚合阶段共计j座风电场聚合后的风电持续功率向量，Z为总持续时间，Pi，jq(q=1，2，…，Z)为第i个聚合阶段共计j座风电场聚合后持续时间为q的风电输出功率。

若采用数理统计法来描述多风电场聚合过程中风电功率概率密度随着装机容量增大而表现出的变化规律，则可用式（2）表示。

式中：Gi，j为第i个聚合阶段共计j座风电场聚合后从装机容量到风电功率概率密度向量的映射；f i，j=[f i，j0，f i，j k，…，f i，j1]T为第i个聚合阶段共计j座风电场聚合后输出功率概率密度向量，k=0，1/M，2/M，…，1为风电功率水平，即将多风电场聚合后的输出功率区间［0，1］p.u.进行M等分，f i，j k为第i个聚合阶段共计j座风电场聚合后在第k个风电功率水平下的输出功率概率密度。

根据历史负荷数据研究多风电场聚合过程中的持续功率曲线与功率概率密度曲线随着装机容量增大而呈现出的变化关系。其中，在多风电场第i个聚合阶段时，通过“装机容量-功率概率密度曲线”的映射关系可得到概率密度曲线，通过“装机容量-持续功率曲线”的映射关系可得到持续功率曲线。数据分析表明，随着参与聚合的风电场数量的增加，各聚合阶段的装机容量逐渐增大，聚合后风电持续功率曲线和功率概率密度曲线逐渐呈现如下非线性变化规律：

1）多风电场聚合过程中风电的持续功率曲线随着装机容量增大呈现头部逐渐降低、中间部分逐渐变宽、尾部逐渐抬高的变化规律；

2）多风电场聚合过程中风电功率概率密度曲线随着装机容量增大呈现头部和尾部逐渐降低、中间部分逐渐抬高的变化规律。

3 多风电场聚合过程中不同装机容量的风电功率概率密度曲线生成

针对风资源不确定性导致的风电功率不确定性，采用数理统计法进行分析是有效的，本文利用概率密度曲线进行分析。

鉴于在描述数据分布特性时，KDE 法［16-17］不依赖于参数估计模型的选择，而且能够有效地避免直方图估计对直方图组距大小和位置的依赖，因此本文采用KDE 法生成多风电场聚合过程中不同装机容量的风电功率概率密度曲线。KDE 法的表达式为：

式中：f̂(p)为风电功率p的KDE 函数；n为样本总数；h为窗宽；K(⋅)为核函数；pm为风电功率p的第m个样本值。

本文选择高斯函数作为核函数，采用经验法则求取窗宽，如式（4）所示。

式中：σ为风电功率样本四分位数。

应用KDE 法获取多风电场聚合过程中不同装机容量的风电功率概率密度分布时会存在边界效应的问题，为此，本文利用一种反射的边界修正方法对边界处概率密度估计值进行修正，该方法在添加以边界为轴的反射数据后求取概率密度，以此来修正KDE 法在边界区域的边界效应，改进KDE 法的表达式为：

式中：pL、pU分别为多风电场聚合后输出功率的下限、上限值。

图3 为修正边界效应前、后多风电场聚合后风电功率概率密度估计曲线。由图可以看出，通过KDE 法生成的风电功率概率密度曲线在输出功率［0，1］p.u.的范围之外有非零值，这显然是不合理的，而通过改进KDE 法生成的概率密度曲线则修正了该误差。

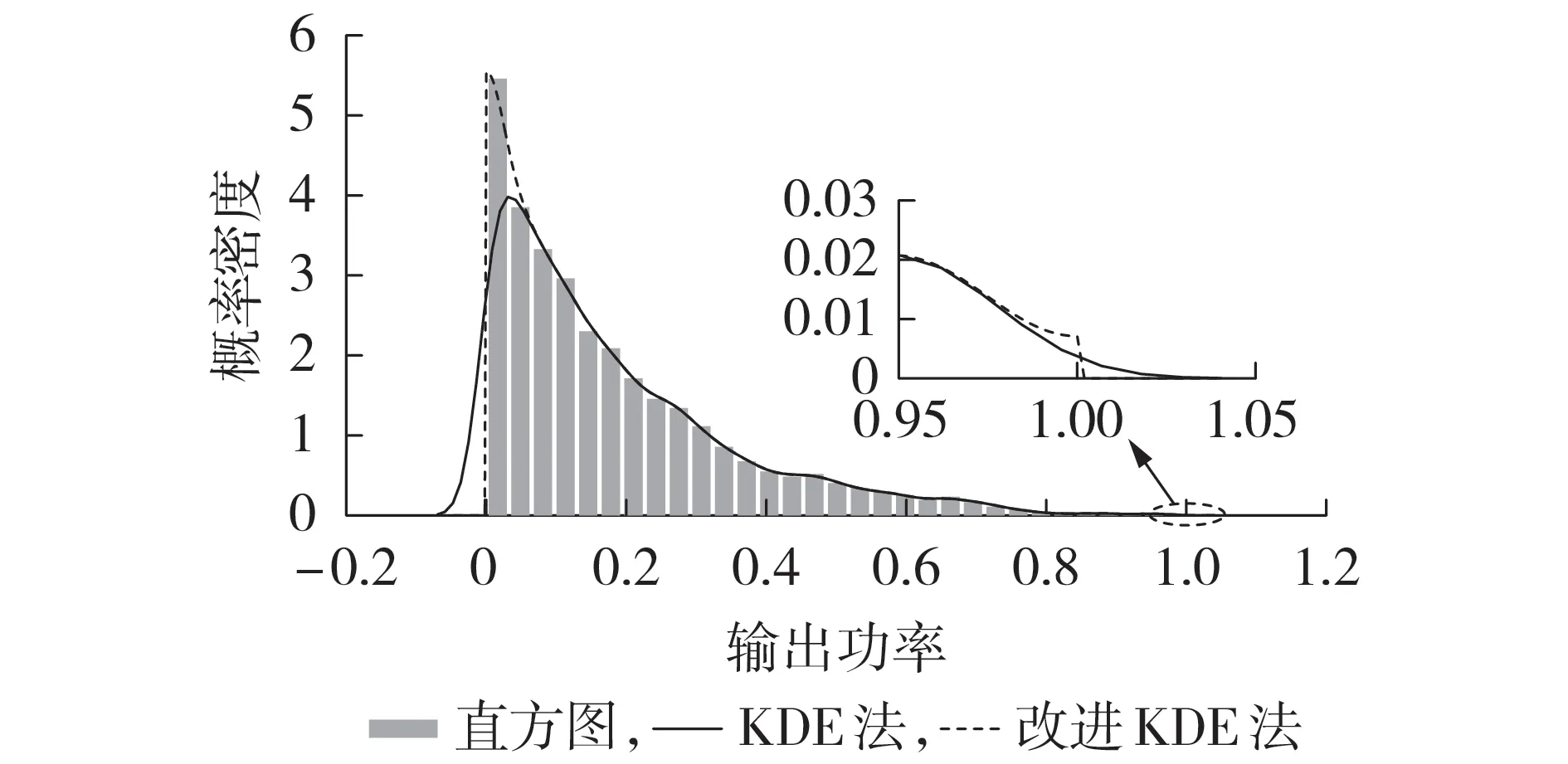
图3 KDE法改进前、后的比较Fig.3 Comparison between before and after improvement of KDE method

4 建立基于GA-SVM的多风电场聚合后输出功率概率密度演变预测模型

鉴于SVM 是基于结构风险最小化原则的有监督学习算法［18-20］，在将其用于回归预测时，其基本原理是利用非线性映射将低维输入变量映射到高维空间，构建线性回归模型，以寻找最优超平面，使得所有样本点距离超平面的总偏差最小，因此本文利用多风电场聚合过程中风电功率概率密度曲线随着装机容量增大而变化的规律，采用SVM 构建多风电场聚合后输出功率的概率密度演变预测模型。SVM的优化目标函数为：

式中：R为优化目标变量；w、bt为最优超平面参数，w为权重向量，bt为第t个时刻的偏移量；c为惩罚因子；ε为不敏感损失函数；ξt、ξ*t为第t个时刻的松弛因子，有如式（7）所示关系；xt、yt分别为训练样本在第t个时刻输入、输出值；φ(⋅)为SVM的核函数。

5 风电功率概率密度分布反演持续功率曲线

对多风电场聚合后在规划目标年的风电功率概率密度分布预测结果进行积分，得到风电功率概率分布曲线，即多风电场聚合后风电功率在［0，1］p.u.区间内不同功率水平的概率值，利用式（9）可计算出多风电场聚合后在规划目标年内不同功率水平的风电功率持续时间，最后将对应输出功率值降序排列即可得到持续功率曲线。

式中：tk为多风电场聚合后风电功率水平为k时的持续时间；Pk为风电功率水平为k时的概率值；[⋅]表示就近取整。

6 实例分析

以我国西北某省已经投运的22 座风电场为例，对多风电场聚合后规划目标年风电功率长期波动特性进行预测。附录A 图A1 给出了该地区风电场的分布及其接入站点信息，可以看出风电场分布范围广且不均衡。

本文将首先建成的17 座风电场（总装机容量为1406.5 MW）的建设年份作为历史年，并将这17座风电场的实测风电运行数据和装机容量作为建模域；将22 座风电场（总装机容量为1 903 MW）均建成的年份作为规划目标年，并将这22 座风电场的实测风电运行数据和装机容量作为预测域。根据风电总装机容量在达到1406.5 MW前各历史年风电功率长期波动特性随装机容量逐渐增大呈现的变化规律，利用所提方法预测风电总装机容量达到1 903 MW 时规划目标年输出功率的长期波动特性。

在建模域中以每个历史年中建设的风电场参与聚合的次序和阶段为例，来说明多风电场在逐步聚合的过程中输出功率随装机容量增大而变化的规律性，如表1所示。

表1 多风电场各汇聚阶段对应的总装机容量Table 1 Total installed capacity of multiple wind farms at each convergence stage

各聚合阶段的风电持续功率曲线如图4 所示。利用改进KDE法生成的对应概率密度曲线见图5。

图4 多风电场聚合过程中不同装机容量下的风电持续功率曲线Fig.4 Duration power curves of wind power during aggregation process of multiple wind farms under different installed capacities

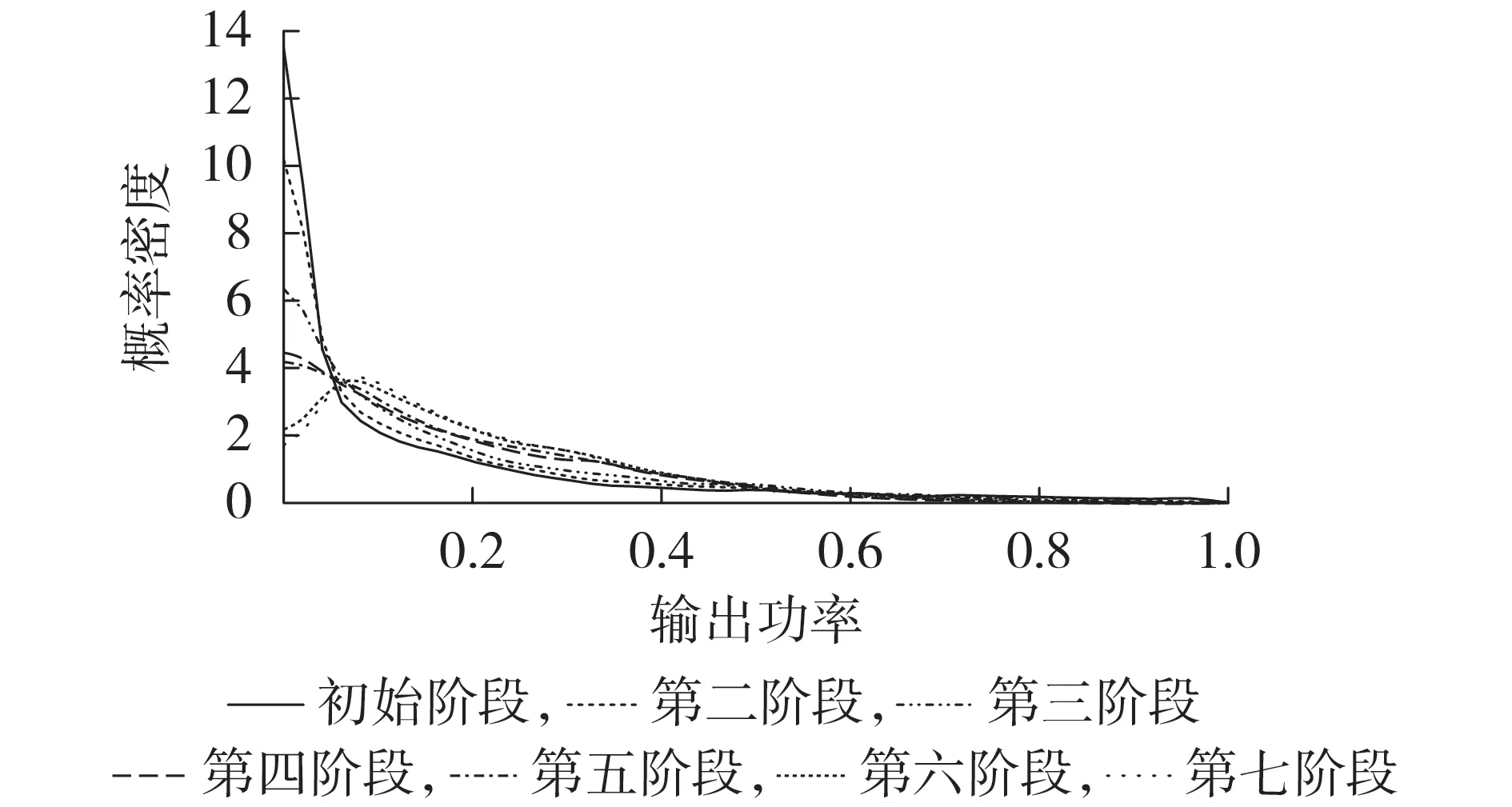
图5 多风电场聚合过程中不同装机容量下的风电功率概率密度曲线Fig.5 Probability density curves of wind power during aggregation process of multiple wind farms under different installed capacities

利用式（1）—（9）实现基于改进KDE 法和GA-SVM的多风电场聚合后规划目标年风电功率长期波动特性预测方法。其中，GA 迭代次数为100 次，种群规模为20 个，惩罚因子c的取值范围为［0，100］，核函数参数γ的取值范围为［0.01，10］。优化目标选择为训练集的交叉验证误差最小，K-折交叉验证K-CV（K-fold Cross Validation）参数为5 折。经过多次试验，GA-SVM 模型输入嵌入维数l为5，风电功率区间等分数M取500，总持续时间Z取8 760 h。另外，为了能够在保证结果合理的基础上节省SVM 训练时间，将接入场站相同的风电场聚合成一个等效风电场群。为避免建模域中由于多风电场聚合顺序的特定选择可能给规划目标年预测结果带来的不利影响，综合考虑建模域17 座风电场所有可能的聚合顺序，将等效后的风电场按排列组合方法进行聚合，模拟多风电场聚合发展过程建立建模域样本，并对装机容量相同的样本进行合并，化简样本容量，根据聚合后呈逐渐递增趋势的风电装机容量序列长度确定聚合阶段总数I，得到建模域样本容量。

利用式（7）计算得到多风电场聚合后规划目标年的风电功率概率密度曲线，如附录A 图A2中红色曲线所示。采用前馈型反向传播BP（Back Propagation）神经网络和反馈型Elman 神经网络作为对比，对与GA-SVM 模型相同的风电功率概率密度样本进行训练和预测，通过试值法设置BP 神经网络和Elman 神经网络的输入层、隐含层和输出层节点数分别为6、4、1，训练次数为1 000 次，学习率为0.01，训练函数为trainlm方法。采用各方法得到多风电场聚合后规划目标年的风电功率概率密度曲线，如附录A 图A2所示。各方法的预测精度对比如表2所示。

表2 概率密度预测精度评估结果Table 2 Evaluation results of prediction accuracy for probability density

由附录A图A2和表2可知，相比于BP、Elman神经网络，采用结构风险最小化的GA-SVM 得到的多风电场聚合后输出功率概率密度曲线的预测结果误差明显更小，预测精度明显更高。

通过式（8）对GA-SVM 预测出的规划目标年风电功率概率密度进行反演，得到多风电场聚合后规划目标年风电的持续功率曲线，如图6所示。图6中同时给出了最小二乘趋势外推的线性回归法的预测曲线以及实测的风电持续功率曲线进行对比。

图6 多风电场聚合后规划目标年风电持续功率曲线预测结果Fig.6 Prediction results of duration power curves of wind power for multiple wind farms after aggregation in planning target year

附录A 图A3 给出了通过2 种方法得到的多风电场聚合后规划目标年风电持续功率曲线的预测误差曲线。采用均方根误差和平均绝对误差评价不同方法的预测效果，如表3 所示，表中均方根误差、平均绝对误差、最大绝对误差均为标幺值。

表3 误差指标对比Table 3 Comparison of error indexes

由图6、附录A 图A3 和表3 可知，本文提出的基于改进KDE法和GA-SVM的多风电场聚合后输出功率长期波动特性预测方法，在评价预测结果的4 个误差指标方面均远优于最小二乘趋势外推的线性回归法。

此外，对KDE 法改进前、后对规划目标年多风电场聚合后输出功率长期波动特性预测结果的影响进行分析。采用KDE 法建立多风电场聚合过程中输出功率概率密度样本，同样利用GA-SVM 采用相同预测模型进行预测，KDE法改进前、后的预测结果如图7和图8所示。

图7 风电功率概率密度预测曲线对比Fig.7 Comparison of predicted probability density curves for wind power

图8 KDE法改进前、后持续功率曲线预测结果对比Fig.8 Comparison of prediction results of duration power curves between before and after improvement of KDE method

由图7和图8可知，在求取风电功率概率密度分布时采用改进KDE 法可有效解决边界效应问题。KDE 法改进前、后最大发电小时数预测绝对误差分别为237 h 和5 h，年满发利用小时数预测绝对误差分别为12 h和1 h，可见改进KDE法有效提高了预测精度。

7 结论

本文提出一种用于预测规划目标年多风电场聚合后输出功率长期波动特性的方法，得到如下结论。

1）揭示了多风电场聚合后输出功率长期波动特性随着装机容量的增大而呈现的非线性变化规律。突破了传统风电功率预测方法必须在装机容量一定的情况才能使用的约束条件，为实现在风电装机容量发生变化的未来年场景下有效预测风电功率长期波动特性奠定了理论基础。

2）给出了一种在没有新建风电场输出功率数据的情况下，准确刻画规划目标年含新建风电场的多风电场聚合后输出功率长期波动变化特性的方法。

3）在利用改进KDE法和GA-SVM预测多风电场聚合后规划目标年的风电功率长期波动特性的过程中，采用持续功率曲线法和数理统计法相结合的方法，该方法更适用于表征和刻画含大规模风电的电力系统规划中风电功率长期波动特性，与现有方法相比，本文方法具有更高的预测精度。

鉴于规划期风电场建设的容量、位置和数量等因素都会对规划目标年风电功率长期波动特性预测精度产生影响，笔者计划下一步对计及这些因素的风电功率长期波动特性开展深入研究。

附录见本刊网络版（http：//www.epae.cn）。