考虑规模化储能的配电网电压分布式控制

王 枭，何怡刚，马恒瑞，刘小燕，张 慧，高文忠

（1. 武汉大学电气与自动化学院，湖北 武汉 430072；2. 青海大学新能源光伏产业研究中心，青海 西宁 810016；3. 丹佛大学电气与计算机工程系，美国 丹佛 80208）

0 引言

加快储能有效融入电力系统发、输、用各环节，对于保障电力可靠供应与新能源高效利用进而实现“双碳”目标具有重要意义［1］。传统集中式储能受地理条件等因素的限制，装机容量增速呈逐年下降趋势；相比之下，需求侧分布式储能技术正得到迅速发展。近年来，信息通信技术的应用赋予分布式储能自主参与电网调控的能力，通过微电网、虚拟电厂、主动配电网等方式实现有效的潮流管理，就地解决系统中局部电压支撑等问题［2-3］。分布式储能是需求响应的重要功率来源，具有容量小、数量规模大、灵活性高、响应速度快等特点。那么，如何协调这些覆盖辽阔地理区域的多元化储能设备，为电力系统提供快速、有效的局部电压支撑，是规模化储能资源利用所要解决的重要问题。因此，有必要开展基于规模化储能的配电网电压分布式控制研究，从而达到快速平抑可再生能源出力对电网电压影响的目的。

配电网的电压调节可以采用集中式的控制结构，由控制中心调度区域内所有的分布式储能设备。考虑到未来电网中将存在大量可用的储能资源，集中式控制需实时感知设备与电网状态并下发控制指令，控制中心的数据吞吐量大、计算负担重，导致通信成本过于高昂，因而无法有效提高风、光等可再生能源的消纳水平。采用相邻通信原则的分布式控制具有抗干扰性强、扩展性好、即插即用和保护隐私等优点［4］，更适合当前背景下分布式储能系统的协调调度，也符合电力系统去中心化的总体趋势。在分布式控制结构中，由信息网互联的储能设备可视为具有决策能力的智能体，多智能体间通过相互配合以实现协同控制的目的［4］。

常见的分布式电压控制方法有一致性控制和分布式优化2 种。一致性控制方法是多智能体网络的主要控制手段，被广泛应用于孤网状态下的微电网控制，可直接同步分布式电源节点上的电压［5］。在一般的大电网系统中，更多的研究采用主从一致性方法，令分布式发电设备集群具有主动参与电力系统调控的能力，如文献［6］中的多智能体领导者采用简单的比例积分（PI）控制调整一致性平衡点，但只可用于电网关键节点的电压调节。相比于单纯实现储能设备间的一致性，系统运营商或储能设备提供商更希望优化配置其管理下的储能资源，在满足电网服务要求的基础上降低设备使用成本，使收益最大化。虽然一致性控制可以通过增量成本一致性，达到类似经济调度的效果［7］，但针对实际物理设备的运行极限，此类方法只能靠限幅环节加以约束。

分布式优化方法为解决规模化储能的优化调度问题提供了统一框架，优化模型的目标函数与储能的使用成本及回报有关，设备及电网的运行限制可在约束条件中体现。分布式优化方法将集中式优化模型分配给各智能体协同解决，能够实现储能资源的快速优化配置，但难点是如何获得具有较好收敛性的分布式求解算法。大量现有研究将分布式优化方法应用于电力系统的电压调节，如采用交替方向乘子算法ADMM（Alternating Direction Method of Multipliers）、对偶分解法等［8-10］；文献［11］提出了基于梯度投影法的分布式电压控制方法，在优化问题的求解中利用与电网结构相关的正定矩阵调整变量迭代方向，在保持目标函数下降的同时得到了完全分散式的控制率；基于相同的思路，文献［10］采用的对偶下降法收敛速度更快，但要求输电线路具有均一的阻抗比以及设备间的两跳相邻通信。相较于上述文献采用的一阶优化方法，ADMM 在实际应用中体现出了更好的收敛性与鲁棒性［12］。文献［13］给出了基于ADMM 的配电网电压控制方法，与文献［14］采用的分布式电压控制相似，信息网中每个智能体自身优化问题中需包含相邻节点的耦合变量，通过一致性约束解决了经典ADMM 中要求中央协调单元的缺点，但这类方法增加了各节点决策变量数，加重了计算及通信负担，更适合微电网群或区域电力系统间的协调调度，且难以应对优化模型中的强耦合约束。文献［2］给出了一种无需迭代求解的分布式电压控制，节点电压估算需沿着配电网辐射方向序贯进行，因而难以适用于节点数较多的电网系统。

基于上述分布式电压控制方法的适用场景及规模化储能的运行特点，本文提出了一种面向规模化储能的电网电压完全分布式控制策略。首先，针对本文研究问题建立优化模型，在模型预测控制MPC（Model Predictive Control）框架内构建了问题的数学描述；然后，基于改进型ADMM［15］，利用优化模型的对偶一致性转换，实现了优化模型的完全分布式求解；最后，通过仿真算例验证了所提方法的有效性与适用性，当储能设备数量显著增加时，能够在有限的时间内给出最优的储能功率设定，在超大规模储能系统的开发利用中体现出了更好的扩展能力。

1 电压控制模型

本节建立了以配电网潮流方程为基础的储能电压支撑问题数学描述，为后续分布式求解算法提供模型基础。

1.1 配电网潮流模型

配电网的拓扑结构可通过图论模型构建，图论模型为G=(N，E)，其中G为有向图，N 为配电网中所有节点的集合（除公共连接点外），N 中的元素个数为N，E为输电线路集合。典型的配电网一般具有辐射状结构，可用线性的DistFlow 模型描述线路潮流与节点电压之间的关系［11］，即：

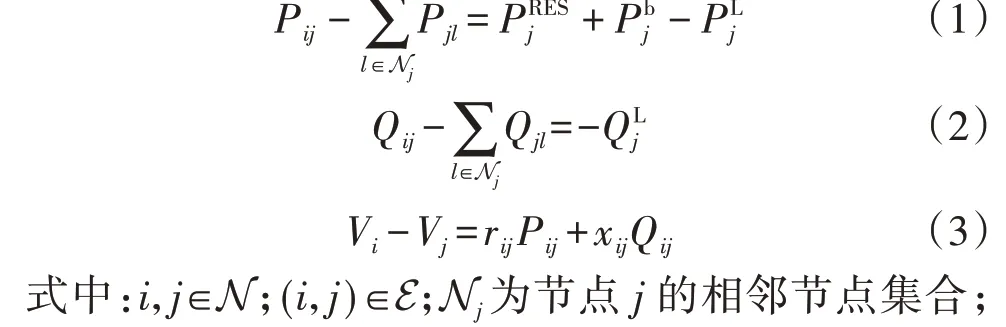
式中：M为G 的关联矩阵；Dr、Dx分别为E 中所有线路电阻、电抗组成的对角矩阵。R、X可视为配电网节点电压与注入功率的敏感度矩阵，一般不具有稀疏性结构。

1.2 考虑配电网电压支撑的优化问题建模

基于优化的控制方法能够系统解决电网的电压控制问题，使电网与分布式储能设备的运行约束得到满足。考虑到一般中低压配电网较高的阻抗比，系统的有功潮流对电压的影响更为明显［10］，因此本文仅考虑储能系统的有功控制，但本文所提出的控制框架可推广到同时考虑储能有功、无功支持的情况。单一储能设备的充、放电通过底层的换流器控制实现，在本文考虑的时间尺度下，可忽略换流器控制回路的暂态过程。考虑到储能系统模型的时间耦合特性，本文基于MPC 框架，针对未来一段时间范围H构建优化模型。

假设配电网每个节点都连接有一个储能设备，对于i∈N，在任意时刻有：

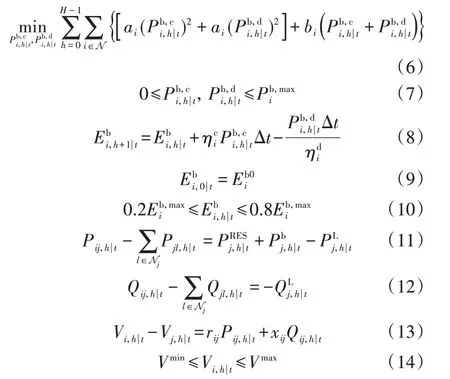
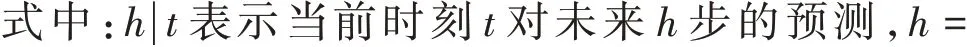
2 基于对偶一致性ADMM 的优化问题快速分布式求解

分布式优化方法一般利用优化模型设计的稀疏性特点，在问题迭代求解的过程中寻求解的分布式计算。相比于一般的一阶分布式优化方法，ADMM采用问题的增广Lagrangian 函数，在大规模优化问题求解中体现出更快的收敛速度［12］。针对上述得到的MPC 优化模型（式（6）—（14）），首先得到优化模型的标准形式；然后基于原始问题的对偶形式转换，利用一致性ADMM 实现优化问题的完全分布式求解。图1 给出了实现分布式求解过程中，优化模型间的转换关系。

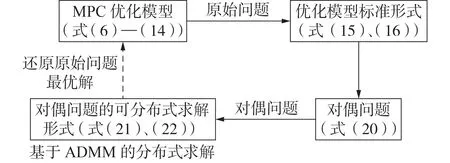
图1 优化模型间的转换关系Fig.1 Transformation relation among optimization models

2.1 优化模型的标准形式

分析优化模型中的耦合与非耦合约束条件，将其表示为如下标准形式（式（15）为目标函数，式（16）为耦合约束），以方便后续的分布式求解。

2.2 基于对偶一致性ADMM的优化模型求解

针对优化模型标准形式（式（15）、（16））开展分布式求解方法研究，经典ADMM 一般需采用中央协调单元单独构建优化问题处理耦合约束（式（16）），因而无法实现完全分布式的优化模型求解。考虑到中央协调单元可能具有与原始优化问题相似的变量规模，算法迭代时间将大量消耗于此，因此其计算复杂度将随着设备数量增加而显著提高，表现为扩展性上的不足，难以应对大规模的优化问题求解［17］。为了克服传统ADMM 的不足，文献［18］首次提出考虑一致性约束的改进ADMM，实现了弱耦合约束优化问题的分布式求解；文献［19］进一步将该方法推广到优化模型中包含全局等式约束的情况，即强耦合约束条件中包含问题的整个决策变量空间；针对具有全局不等式约束的优化问题，文献［15］提出一种分布式求解方法，可更好地解决本文考虑的分布式电压控制问题。

首先，将约束条件（式（16））表示为等式约束的形式，具体如下：

式中：fi(xi)表示原始问题的目标函数（式（15））；y∈R2N×H-，为耦合约束（式（16））的对偶变量；trace{·}表示矩阵的迹。

然后，根据式（18）的Lagrangian 函数得到如下对偶函数：

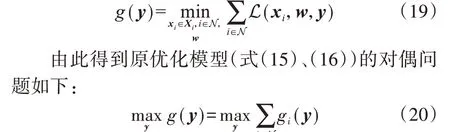
根据式（19）的表达形式可知，对偶问题（式（20））具有可拆分的目标函数。假设对偶间隙为0，可通过求解对偶问题还原原始问题的最优解。

为了实现对偶问题的分布式求解，考虑网络中各节点目标函数gi(yi)，以对偶变量y的本地副本yi∈R2N×H为决策变量，引入一致性约束条件使其收敛到相同值，即得到对偶问题（式（20））的可分布式求解形式如下：

3 仿真算例

为了验证所提算法在实现大规模储能设备协同调压中的有效性，本文基于IEEE 33 节点系统［20］对调压效果进行了分析，比较了集中式优化方法与分布式优化方法的控制效果，讨论了所提方法的扩展能力。

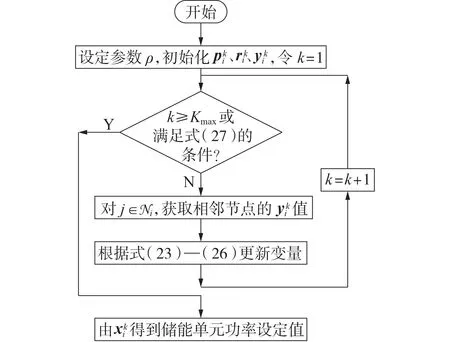
图2 储能分布式电压控制策略流程图Fig.2 Flowchart of distributed voltage control for energy storage devices

附录A 图A1 给出了分布式控制结构下储能设备与配电网示意图，其中聚合商可视为一系列储能设备的领导者，其职责是接收电力系统运营商的服务控制请求，并分配所获收益。电力系统、储能设备及其分布式控制系统组成了物理信息网络。IEEE 33节点系统参数可由文献［20］获得。

3.1 仿真设置

储能设备的额定参数（额定功率、额定能量、充电效率、成本系数）在给定的范围内随机产生，其参数范围如附录A 表A1 所示，所有储能设备的初始SOC值设为50%，充、放电效率取值相同。储能设备的通信网络可完全独立于配电网结构，这里仅要求网络图论模型的无向性与连通性［15］；因此，假定分布式储能具有环状的通信网络结构，对于储能设备｛1，2，…，N｝，其在配电网中的接入节点随机选择，每个储能设备包含5 个相邻的储能设备，忽略通信延时。仿真实验中，在配电网随机接入了11 个光伏发电系统，24 h 内的光伏发电情况见附录A 图A2（a），采样周期为5 min，该数据可由文献［21］获得。

此外，仿真中随机选择了10 个功率消耗随时间变化的有功负荷，其数据可由文献［22］获得，负荷的功率变化情况见附录A 图A2（b），负荷功率基准为IEEE 33 节点系统的原始运行点。配电网允许的电压范围设为0.95～1.02 p.u.，配电网公共连接点处的电压设为1 p.u.。对于本文所采用的分布式优化算法，ρ设为0.01，算法循环的退出条件为：

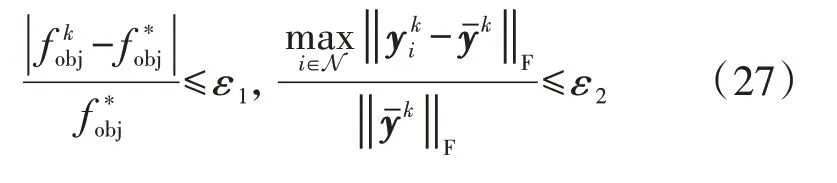
仿真实验中的优化问题采用YALMIP 调用优化程序CPLEX 求解，仿真步长与Δt均设为5 min，仿真总时长为24 h，MPC 的预测时长H设为1 h。本文使用一台Core i5 16 GB 的计算机，采用MatPower 对系统进行仿真。

附录A 图A3 给出了无储能支撑下配电网不同节点的电压变化情况。可以看出，无储能电压支撑下，系统部分节点电压位于允许范围之外，在接近中午时光伏出力处于较高水平，电网电压升高明显。

3.2 算例1：IEEE 33节点系统调压效果分析

在该仿真算例中，基于对偶一致性ADMM 的分布式调压效果见附录A 图A4，所有分布式储能设备的充、放电功率与SOC 情况见附录A 图A5。可以看出：储能设备大部分时间工作于放电状态，支撑配电网电压使其位于0.95 p.u.以上；在光伏系统出力明显升高时（10:00—15:00），储能系统工作在充电状态，保证部分节点电压不超过1.02 p.u.的上限，且未发生储能充、放电功率同时非零的情况。图3 比较了优化模型在集中式优化与分布式优化下的目标函数值。综上可见，本文采用的分布式电压控制能够得到与集中式优化相似的储能运行成本与电压支撑效果，即收敛到问题的全局最优。

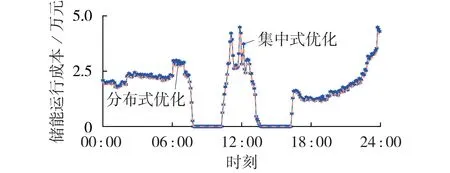
图3 集中式优化与分布式优化下储能设备运行成本比较Fig.3 Comparison of operation costs of energy storage devices under centralized and distributed optimization

3.3 算例2：协同大规模储能的算法扩展性分析

为了进一步验证分布式优化在协同大规模储能设备时的优良特性，本算例比较了不同储能设备数量情况下，集中式优化与分布式优化的计算时间。对系统32 个节点，增加每个节点接入储能设备的数量，用Nsc表示。在仿真分析中，调整了通信网络中每个储能设备相邻节点的数量，以加快算法收敛。针对不同的储能设备数量，设每台设备的相邻节点数为5Nsc，ρ的值调节为ρ0/Nsc，其中ρ0为Nsc=1 时ρ的取值。针对式（27）中的目标函数和对偶变量收敛性判断条件，图4 给出了Nsc分别取为1、5、10、50（对应的储能设备总数分别为32、160、320、1 600）时，一个控制周期内对偶一致性ADMM 的收敛速度，可见算法能够在适当的循环次数（145 次）达到给定的迭代终止条件，说明分布式优化可以通过优化通信网络结构设计来实现有限迭代次数后收敛［23］。

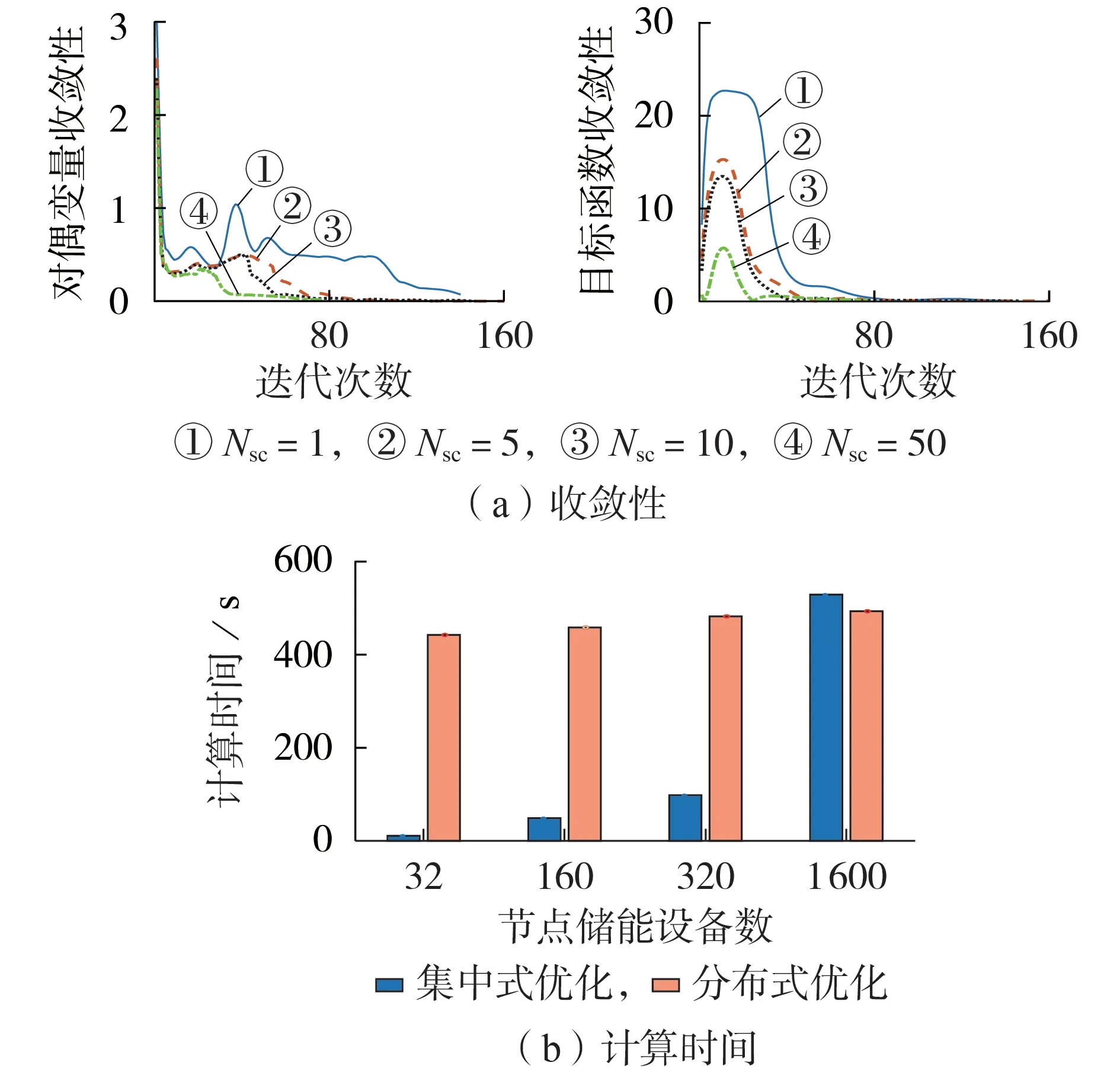
图4 不同Nsc下对偶一致性ADMM的收敛性与计算时间比较Fig.4 Convergence and computation time with dual consensus ADMM under different Nsc values

表1 列出了集中式优化与分布式优化1 次迭代所用时间，分布式优化方法每次迭代的计算时间对问题规模敏感性不高，当系统中每增加1 个储能设备，也对应增加了1个分布式的控制器。从图4可以看出，集中式优化的计算时间随储能设备数量的增加而显著提高，而分布式优化的计算时间随储能设备数量的增加变化不大。这是因为分布式优化框架下，每个储能设备决策变量的长度只与预测时长有关。综合图4和表1的结果可知，分布式优化的计算时间对协同储能设备数量变化的敏感度不高，在储能设备数量较少的情况下，分布式优化的迭代计算导致其所需时间更长，此时集中式优化的计算时间更短，但是随着储能设备数量的增加，集中式优化的计算时间显著提高，而分布式优化的计算时间变化不明显。这表明了分布式优化在协调超大规模分布式储能设备时的优越性。当继续增加每个节点的储能设备数量（Nsc=1000），MATLAB 由于计算机内存不足无法给出结果，这也从侧面验证了集中式优化在处理大规模优化问题时需要大量的存储空间，控制中心更面临设备间通信带宽与时延等问题，因而难以扩展到大规模储能设备的协同控制中。

表1 集中式优化与分布式优化计算时间比较Table 1 Comparison of computational time between centralized and distributed optimization

4 结论

本文针对需求侧大规模储能设备的协同电压调节问题开展研究，提出了基于对偶一致性ADMM 的分布式电压控制方法，能够应对电网系统与储能设备运行约束，为电网提供高效、可靠的电压支撑。仿真结果表明，分布式优化方法具有与集中式优化方法相似的储能设备功率调度与电压支撑效果，在协调大规模分布式储能设备的应用场景中体现出更好的扩展性。

附录见本刊网络版（http：//www.epae.cn）。