基于分形插值的轨压曲线拟合方法

蒲 瑜，苏铁熊，马富康，李良钰，徐春龙

(1.中北大学能源动力工程学院，山西 太原 030051) (2.中北大学机电工程学院，山西 太原 030051) (3.中国北方发动机研究所，天津 300400)

高压共轨柴油机由于高功率、低排放、低油耗等优点，被广泛应用于农业、工业以及交通运输等领域。在运行时，高压共轨系统会通过各种传感器检测发动机的实际运行状况，但受燃油冲击、传感器精度、电磁干扰以及通信故障等因素影响，采集到的轨压曲线会出现缺失值或异常值。因此，研究能较为精确地还原轨压信号的整体变化趋势与局部波动特征的插值方法对研究高压共轨运行状态至关重要。

在使用三次样条插值法[1]、Lagrange插值法[2]等传统插值方法时，由于其两个插值点之间用直线或曲线连接，无法体现插值点之间的局部波动特征，因此在处理类似轨压曲线等波动剧烈的时间序列时不是很理想。李春等[3]将分形插值法应用于一些复杂非线性曲线的插值拟合中；郭秀婷等[4]将纳什效率系数等作为衡量插值精度的指标；喻亮等[5]运用分形插值方法拟合铝电解槽阳极导杆等距时间电压降曲线，证明了在铝电解槽中熔融电解质与铝液界面的波动曲线是非线性的，具有分形特征。代入不同的垂直比例因子，分形插值曲线的形态是不同的，证实了垂直比例因子对分形插值生成的曲线具有一定的影响，将分形插值曲线和传统插值曲线比较,证实了分形插值拟合曲线具有优越性。

本文参考这类非线性曲线的插值拟合方法，将分形插值法应用于轨压曲线的插值拟合中。实验证明，分形插值法相较于传统插值方法如三次样条插值法、Lagrange插值法等可以取得更高的精度。

1 分形插值原理

分形插值法是一种由美国数学家M.F.Barnsley提出的构造分形曲线的方法，它是一种基于IFS(iterated function system, 迭代函数系统)、能够反映插值点之间局部波动特征的插值方法。描述云彩、山脉、森林的轮廓等这些大自然几何体以及非线性变化的曲线时，分形插值法可以得到比三次样条插值法、Lagrange插值法等传统插值方法更高的精度。

设存在一组插值数据C：

C={(xi,yi)∈I×R,i=0,1,2,…,N}

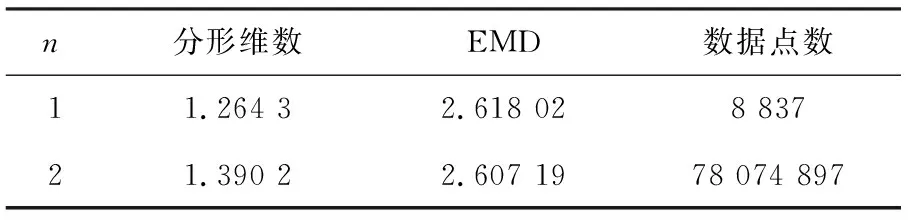
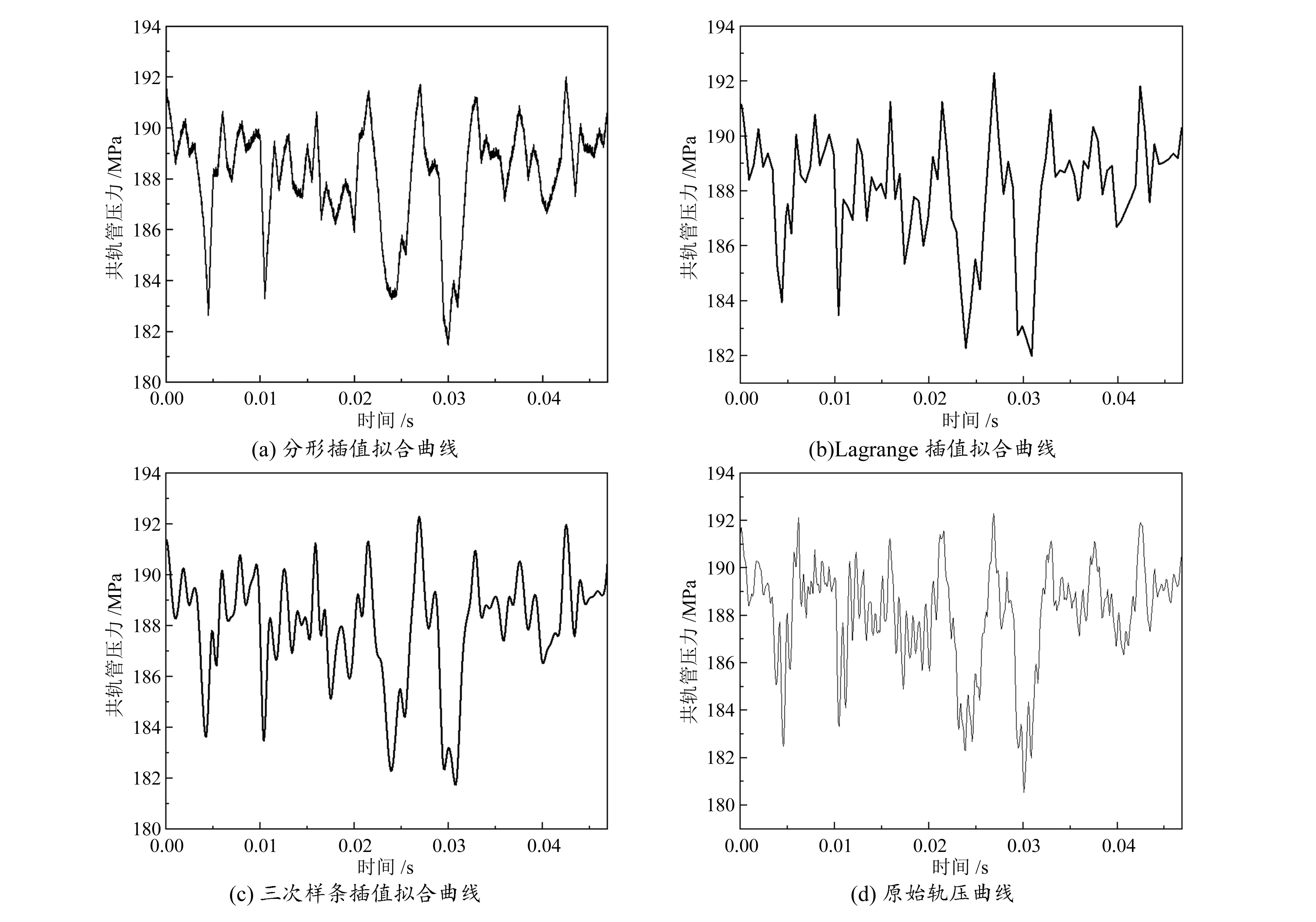
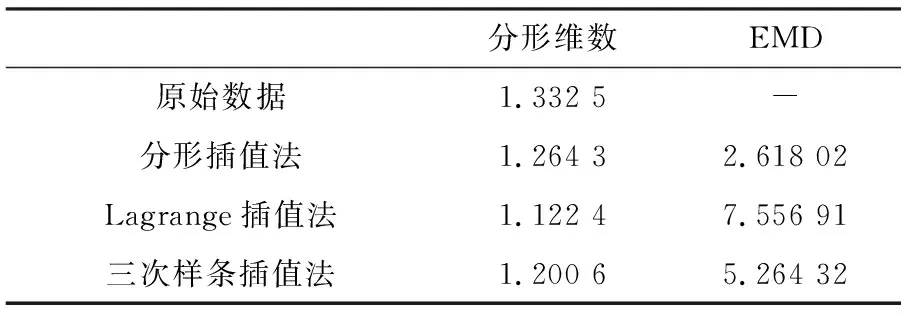
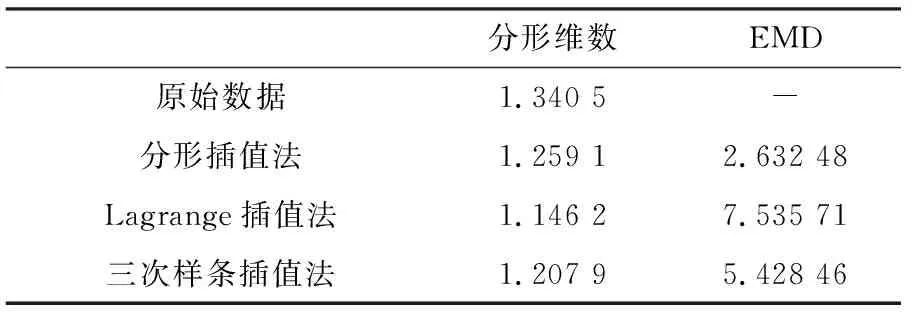
x0

I=[x0,xN]

(1)

式中：(xi,yi)为一组数据点；N为非负整数。f(x)为插值函数，对于每一个xi,都有f(xi)=yi，且插值数据(xi,yi)不共线。

吸引子G={(x,f(x)),x∈(x0,xN)}，为插值数据的连续图像。

设映射函数Wi为：

(2)

且满足如下条件：

(3)

式中：x,y为未知数；ai,bi,ci,di,ei,fi均为常数。

依据IFS的条件推导映射函数可得：

(4)

式(4)中仅di为自由变量，称为垂直比例因子，其他未知数皆可通过代入插值数据获得。本文通过分形维数D衡量插值函数的局部波动特征，可通过式(5)求解：

(5)

由式(5)可知，分形维数仅与自由变量di有关。把插值数据代入式(6)中，迭代到收敛至吸引子G附近，即可完成分形插值拟合。

2 衡量插值方法的指标

EMD(地球搬运距离)是一种通过一次线性规划计算两个几何或向量距离的算法，在评估两个多维分布的差异性方面有着广泛的应用。对于任意两条空间曲线，其EMD值越小，说明其相似性越高，差异性越小；其EMD值越大，说明其相似性越低，差异性越大。

设存在如下两条曲线：

(6)

其中：

(7)

式中：k,l均为正整数；xi∈RH,yi∈RH,Wxi∈R,Wyj∈R,H为正整数。

通过求解式(8)中的最优解得到fij：

(8)

式中：dij为xi与yj之间的距离。

由此得到XY两条曲线的EMD为：

(9)

3 分形插值的实验验证

3.1 实验数据的提取与分析

为提取轨压曲线，对共轨系统进行台架实验。该实验系统包括德尔福(DELPHI)高压共轨式燃油喷射系统、汉斯曼22 kW喷油泵实验台、EMI-II型瞬态参数值测试和分析系统、EFS8233型共轨喷油器电磁阀控制仪、EFS8244型轨道压力控制仪、轨道压力传感器、高精度角度传感器及高强度联轴器等。测试系统如图1所示。

图1 共轨系统实验图

图2所示为共轨系统轨压曲线与频谱图，频谱图的纵坐标P表示该频率在所有计算频率中的占比。该曲线表现出明显的非线性与较强的波动性，且频率混杂严重，频率范围较广。该曲线共有470个数据点，从中提取94个数据点作为初始插值数据。

图2 轨压曲线与频谱

3.2 垂直比例因子对插值曲线的影响

由式(4)可知，确定插值数据后，仅存在垂直比例因子一个自由变量，所以可以认为垂直比例因子是影响插值精度的重要因素。图3是不同垂直比例因子的插值曲线，图4是不同垂直比例因子的分形维数。由图4可以看出，随着|di|的增大，分形插值曲线波动程度随之增大，局部波动特征更加明显，分形维数也随之增大。

图3 不同垂直比例因子的插值曲线

图4 不同垂直比例因子的分形维数

但是分形维数并非越大越好，图5所示为不同垂直比例因子下的EMD值，从图中可以看出，di的取值严重影响插值精度，故本文将EMD作为选取垂直比例因子|di|的依据。当di=-0.035时，EMD最小，为2.618，代表此时分形插值曲线与原始轨压曲线相似度最高，故选取di=-0.035。

图5 垂直比例因子对EMD的影响

3.3 迭代次数对插值曲线的影响

插值点数m与迭代次数n、初始插值点数q之间的关系如下：

m=(q-1)2n+1

(10)

表1为不同迭代次数对各个指标的影响，从表中可以看出，虽然随着迭代次数的增加，插值曲线的误差随之减小，但是迭代次数的增加并不会明显提高插值曲线的精度，却会显著增加计算复杂程度，增加数据点数，故本文中实验的迭代次数采用1次。

表1 迭代次数对各个指标的影响

3.4 分形插值与传统插值方法的对比

分别使用Lagrange插值法与三次样条插值法对轨压曲线进行插值拟合，图6所示为3种插值方法拟合的曲线与原始曲线。从图中可以看出，分形插值法相较于其他传统插值方法可以更好地保留原始轨压曲线的整体变化趋势，并且能够更加精细地还原局部波动特征，而其他传统插值方法由于使用光滑曲线连接插值点，无法还原局部波动特征。

图6 不同插值方法的对比

表2为3种插值方法的EMD值与分形维数对比。由表可知，在表征数据波动程度的分形维数这一指标上，分形插值的分形维数最接近原始数据；在表征插值误差的EMD这一指标上，分形插值的误差最小，比Lagrange插值法减小了65.3%，比三次样条插值法减小了50.3%。

表2 第一次实验插值效果对比

对共轨系统再次进行台架实验，提取轨压曲线。分别使用3种插值曲线进行插值拟合。表3为第二次台架实验所得的轨压曲线3种插值方法的EMD值与分形维数对比。从表中同样可以得出，在表征数据波动程度的分形维数这一指标上，分形插值法最接近原始数据；在表征插值误差的EMD这一指标上，分形插值法的误差最小，比Lagrange插值法减小了67.1%，比三次样条插值法减小了53.2%。

表3 第二次实验插值效果对比

表4为第三次台架实验所得的轨压曲线3种插值方法的EMD值与分形维数对比。从表中同样可以得出，在表征数据波动程度的分形维数这一指标上，分形插值法最接近原始数据；在表征插值误差的EMD这一指标上，分形插值的误差最小，相比Lagrange插值法减小了65.1%，比三次样条插值法减小了51.5%。

表4 第三次实验插值效果对比

相比Lagrange插值法与三次样条插值法等传统插值方法，分形插值法在处理波动较为剧烈的轨压曲线时，可以较好地保持曲线的波动特性，并拥有更高的插值精度，与原始曲线吻合更好，相比传统插值算法具有明显的优势。

4 结论

本文使用分形插值法对轨压曲线的缺失数据进行插值拟合，对分形维数及插值误差随着垂直比例因子的变化规律进行了分析，找到了具有插值误差目标的最佳垂直比例因子，通过与其他传统插值法进行对比，得出如下结论：

1)垂直比例因子是影响分形插值曲线的重要影响因素，选取合适的垂直比例因子可以显著提高分形插值的精度。

2)在处理波动剧烈的轨压曲线插值拟合问题时，分形插值法相比传统插值方法如Lagrange插值法与三次样条插值法等可以在反映局部波动特征的同时，具有更小的插值误差，分形插值曲线的EMD分别比Lagrange插值曲线和三次样条插值曲线减小了65.3%和50.3%。相比传统插值方法，分形插值更具有优势。