隔震结构-设备组合体系的优化设计研究

党 育，王宝平，李国宝

（兰州理工大学土木工程学院，甘肃兰州 730050）

引言

国内外多次地震的震害经验显示：隔震技术能有效减轻地震作用，提升房屋的抗震设防能力，因此，对一些使用功能有较高需求的建筑，如医院、变电站、电信控制中心、金融系统（银行、证券、保险）的信息和数据中心等，多采用隔震技术来提高抗震性能。这些建筑物内精密仪器设备密集，且在人们的生产生活和抗震救灾中起着关键作用，一旦设备破坏，中断运行，会影响整个建筑甚至整个行业系统的正常工作，造成巨大的经济损失。对这类放置有重要设备的功能性隔震结构，整个建筑的抗震性能主要由设备的抗震性能决定。虽然隔震技术可减小地震作用，改善设备的抗震安全性，但由于设备与结构之间具有复杂的动力相互作用，且设备和结构具有不同的动力响应特性和设防要求，而目前的隔震结构设计是将设备作为等效静荷载，忽略结构与设备的动力相互作用，仅依据结构的抗震性能进行隔震设计，不考虑设备的抗震安全性。特别是当设备与楼层的质量比超过1%时，设备与结构的动力相互作用不能忽略［1］，而此时设备对结构的作用类似于一个调谐质量阻尼器（TMD），设备的动力参数还会影响到隔震结构的减震效果。所以，对于放置有设备的功能性隔震结构，目前的设计方法并不能完全保证设备安全、维持建筑功能，应该将隔震结构-设备作为一个组合体系，考虑隔震结构和设备的动力相互作用，并同时满足隔震结构和设备的抗震安全，进行相应的隔震结构设计。

对于隔震结构-设备组合体系的研究，主要集中于动力分析和试验验证方面。2011 年～2014 年NEES/E-Defense 对一个全比例医院隔震建筑进行实验［2－3］。研究发现：采用隔震技术，在近断层地震中，医院仍可维持功能，但在俯冲型长周期长持时地震中，家具和有脚轮的医疗设备会有较大位移，医院部分区域功能中断。KONSTANTINIDIS 等［4］讨论了隔震系统参数对不同摩擦系数的设备滑移反应的影响，结果发现：隔震一般可有效减小设备的滑动，但在一些特殊位置，特别是在高烈度时或低摩擦系数时，隔震会增加设备的滑动；国巍等［5］采用随机振动的方法，分析了非线性主体结构对子结构动力响应的影响规律；韩淼等［6］将隔震结构和设备均简化为线性，考虑隔震结构与设备的相互作用，分析了设备质量、设备阻尼比和隔震层阻尼比等因素对楼面反应谱的影响；周经纬［7］分析了主子结构频率比、质量比和阻尼比对系统动力特性的影响，最终取质量比下的各参数的平均值作为主子结构的最优参数。另外，研究者提出在隔震结构中增设TMD，或者将结构中的一部分设置为TMD，以减小隔震结构的位移，并给出了TMD的最优参数［8－10］。

以上研究说明：在设计分析隔震结构时，需要更加明确设备的反应。同时，当设备与楼层的质量比超过1%时，设备对主体结构的作用类似于TMD，但参数必须配置得当才能起到减震作用，而且设备除了减小主体结构的振动外，自身也要减震，直接采用隔震结构-TMD的优化参数并不合适。因此，本文针对隔震结构-设备组合体系，考虑隔震结构与设备的相互作用和非比例阻尼影响，给出了一种隔震结构-设备组合体系的优化设计方法，该方法基于多种群遗传算法，得到隔震层和设备的最优动力参数，使设备和隔震结构同时满足抗震安全。

1 考虑动力相互作用的隔震结构-设备组合体系运动方程

隔震结构-设备组合体系的计算简图如图1所示，隔震结构简化为层剪切模型，共n+1层，设备简化为一个线性单自由度体系，位于第i层。图中，mb、kb和cb分别为隔震层的质量、刚度和阻尼，m1～mn、k1～kn和c1～cn分别为上部结构各层的质量、刚度和阻尼，将设备类似于TMD，me为设备的质量，ke和ce分别为设备与结构连接处的刚度和阻尼。由此，可写出隔震结构-设备组合体系的运动方程为：

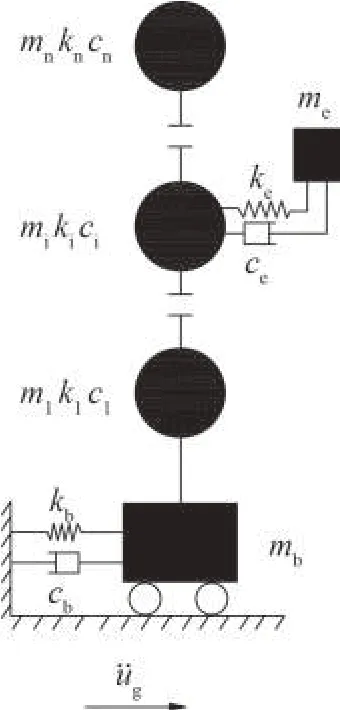
图1 隔震结构-设备组合体系计算简图Fig.1 Calculation diagram of isolated structure-equipment composition systems

C为组合体系的阻尼矩阵，由于隔震结构中隔震层与上部结构阻尼特性截然不同，同时，设备阻尼也与上部结构不同，对于这类典型的非比例阻尼结构，可采用分区瑞利阻尼，得到隔震结构-设备组合体系的阻尼矩阵：

式中：C0为组合体系的瑞利阻尼矩阵：

Cr为考虑隔震层和设备的余项阻尼矩阵：

αb、βb、αs、βs、αe和βe分别为隔震层、上部结构和设备的瑞利阻尼比例系数：

式中ωn和ωm为组合体系第n阶和第m阶振型频率；ξb、ξs和ξe分别表示隔震层、上部结构和设备的阻尼比。

由此，可依据以上公式进行动力分析，得到隔震结构-设备组合体系的响应。

2 隔震结构-设备组合体系的优化方法及实现

2.1 优化模型

隔震结构-设备组合体系的动力响应不仅与隔震结构和设备的动力参数有关，还与设备所在楼层、设备与结构的质量比、频率比有关。但如果将隔震结构和设备的所有动力参数均选为优化参数，会使该优化问题过于复杂。从已有研究可知［1］：设备位于不同楼层位置对设备的动力响应影响较小，误差不超过5%，因此，设备所在位置不作为优化参数。其次，虽然设备与结构的质量都会显著影响组合体系的动力响应，但在实际的工程设计时，设备质量和结构质量都很难调整，也不作为优化参数。最后，由于隔震结构的动力响应主要由隔震层参数决定，上部结构的动力参数也不作为优化参数。这样，最终选取隔震结构-设备组合体系的优化参数为：隔震层刚度kb、隔震层阻尼cb、设备与结构连接处的刚度ke和阻尼ce。

为了优化设计方便，以上各阻尼系数用阻尼比代替，则隔震结构-设备组合体系的优化参数为：

式中：kb为隔震层的水平等效刚度；ξb为隔震层的等效阻尼比；ke为设备连接处刚度；ξe为设备连接处的阻尼比。

对于隔震结构-设备组合体系，既需要保证隔震结构的抗震安全，还需要保证设备的功能维持。对于隔震结构，抗震安全意味着上部结构在设防地震时层间位移角满足相应要求，且在罕遇地震时隔震层位移不超过限值。对于设备，参考《石油浮放设备隔震技术标准》（SY/T0318-98）［11］，该标准不仅适用于石油设备，对于其他浮放设备也有很好的适用性［12］。该标准要求，在设防地震作用下，设备应不受损坏并且维持正常运行。同时，将设备分为加速度敏感型和速度敏感型，对应的设备抗震能力用容许加速度或速度来表示。因此，设备功能维持意味着设防地震时设备加速度或速度满足容许值。也就是说，隔震结构-设备组合体系的设计需要满足以上3个目标，对于这样一个多目标优化问题，可将3个目标进行归一化处理，并认为各目标同等重要，将3个目标值进行平均。由于本文设定的设备与精密机床相似，是加速度敏感型。这样，目标函数可写为：

式中：ae为设防地震下设备的最大加速度；aemax为设防地震下设备的加速度限值，应按照制造部门提供的设备耐震指标确定，若无法提供该指标时，可通过试验法或类比法得到［11］；θs为设防地震下，上部结构各层中最大层间位移角；θmax为最大层间位移角的限值。对于设置有重要设备的功能性隔震结构，依据《建筑隔震设计标准》（送审稿）［13］的要求，设防地震下主体结构基本不受损坏或不需修理即可继续使用，对于钢筋混凝土框架结构，θmax=1/400；ub为罕遇地震作用下，隔震层最大水平位移；umax为隔震层的水平位移限值，依据《建筑抗震设计规范》（GB50011-2010）［14］的要求，umax=min(0.55D,3tr)，D为支座的有效直径，tr为支座内部橡胶总厚度。

则约束条件为：

这样可得到隔震结构-设备组合体系的优化模型如式（14）至式（18）。

2.2 优化方法及步骤

尽管以上优化模型中，目标函数和约束条件均与设计变量存在一定联系，但无法用函数关系式严格地表示出来，因此，难以构建出满足传统优化方法要求的数学模型，此外，对于复杂优化问题，传统优化方法很难给出全局最优解。因此，选用多种群遗传算法（Multiple Population Genetic Algorithm，MPGA）对该问题进行求解。多种群遗传算法通过扩展优化搜索种群，借助移民算子和人工选择算子，显著提高了遗传算法的局部和全局搜索能力，并增加了优化效率［15］。

本文用MATLAB 的Sheffield 遗传算法工具箱和文献［16］给出的移民算子函数immigrant（）和人工选择算子函数EliteInduvidual（），实现隔震结构-设备组合体系的参数优化的MPGA 求解，优化流程如图2 所示，具体步骤如下：

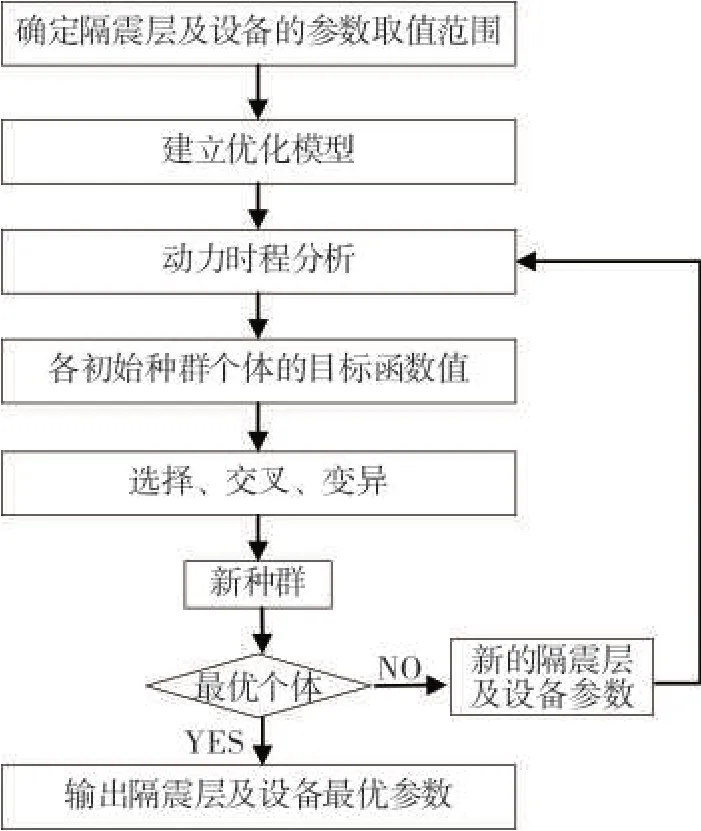
图2 隔震结构-设备组合体系的优化流程Fig.2 Optimization flow of isolated structure-equipment composition systems

（1）根据支座在重力荷载代表值下的竖向压应力限值要求，预判隔震支座直径大小，给出设计变量kb和ξb的取值范围，考虑设备与结构的连接方式，给出设计变量ke和ξe的取值范围，用MATLAB 的遗传算法工具箱，对各设计变量进行二进制编码形成位串，随机生成多个独立的初始种群；

（2）将各初始种群的参数解码后，与上部结构组成隔震结构-设备组合体系的动力分析模型，进行动力时程分析，求得各初始种群对应的结构响应；

（3）用求得的各结构响应计算约束条件和目标函数值，若约束条件中有一个不满足，则采用惩罚策略，将目标函数值扩大数倍；

（4）将求得的目标函数值再传递到MATLAB 遗传算法工具箱，经过编码得到种群中个体的适应度；

（5）对个体进行选择、交叉、变异以及移民运算，生成新种群，并在每个进化代中，借助人工选择算子筛选出各种群中的最优个体，保存在精华种群中；

（6）重复步骤（2）～（5），直至精华种群中最优个体的最少维持代数满足设定的终止条件，程序结束。

另外，在优化过程中，隔震层参数和设备参数不断改变，会导致结构周期变化，要满足输入地震动的频谱和持时等特征与结构模型匹配，需要不断改变输入的地震动，这不仅影响了优化效率，还使得时程分析的结果离散性较大，为了简化分析并保证地震波满足设计要求，取地震动为标准人工波，即：在设防地震和罕遇地震时，分别输入1条人工波，该人工波有足够的持时，且对应的反应谱与规范设计反应谱在各周期点的误差均小于5%。这样无论隔震层参数和设备参数如何改变，标准人工波均可满足时程分析的选波要求。优化过程中所选用的地震动如图3所示。

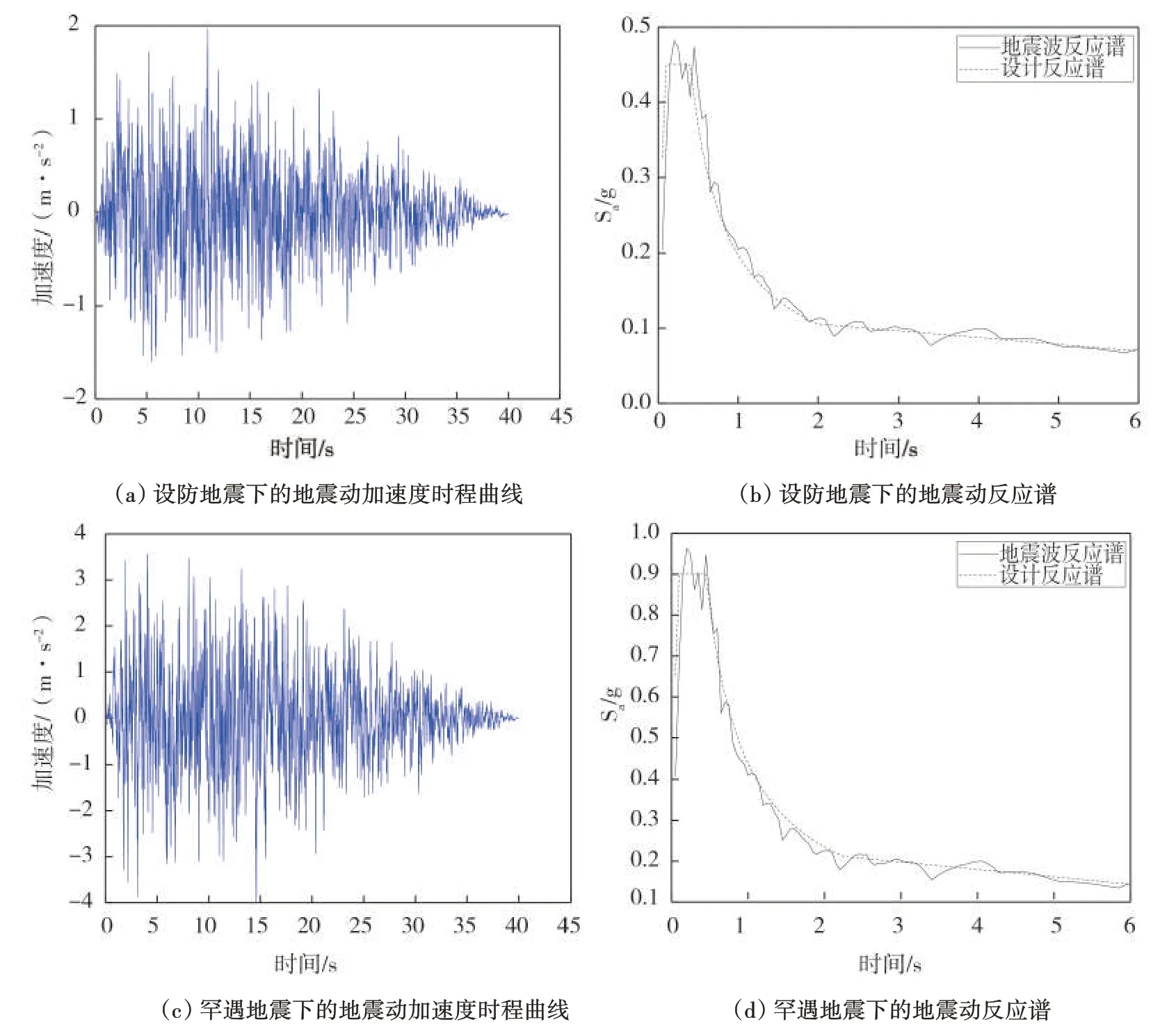
图3 优化过程中用的标准人工波Fig.3 Standard artificial waves used during the optimization process

3 工程实例及分析

3.1 隔震工程概况

某实际隔震结构，乙类建筑，地上6 层，建筑高度21.6 m，上部结构为钢筋混凝土框架结构。设防烈度8度（0.2 g），设计地震分组第二组，场地类别II类。隔震层质量为63 831 kg，上部结构各层质量和刚度见表1。设备放置在第三层，质量13 000 kg，设备与楼层的质量比为1.6%，大于1%，设备与结构的相互作用不可忽略。设备自振频率22.5 rad/s，设备所能承受的最大加速度为200 cm/s2。原设计共有38 个隔震支座，支座布置如图4所示。隔震支座的力学性能参数见表2。

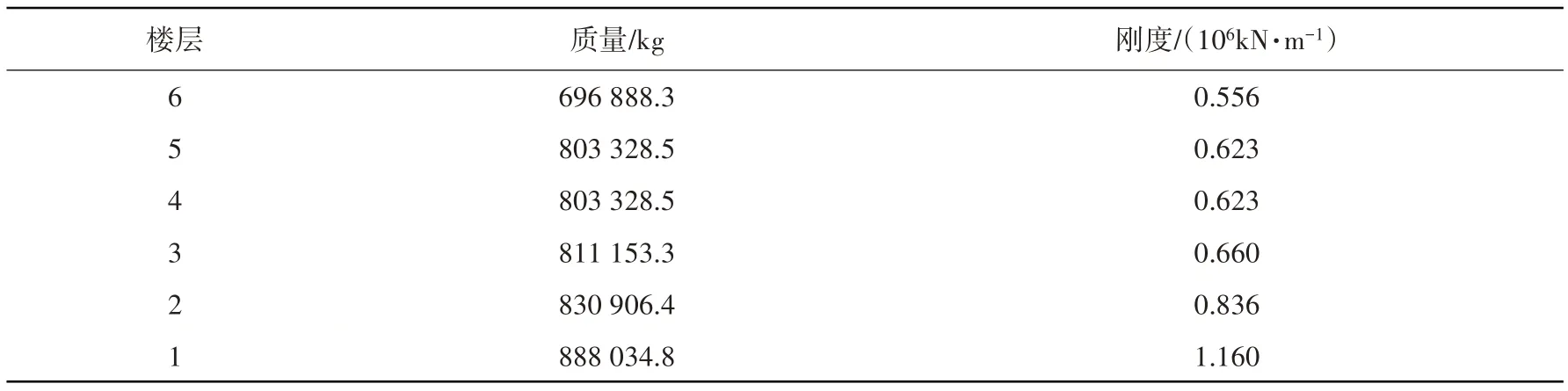
表1 上部结构各层质量和刚度Table 1 Mass and stiffness of the superstructure

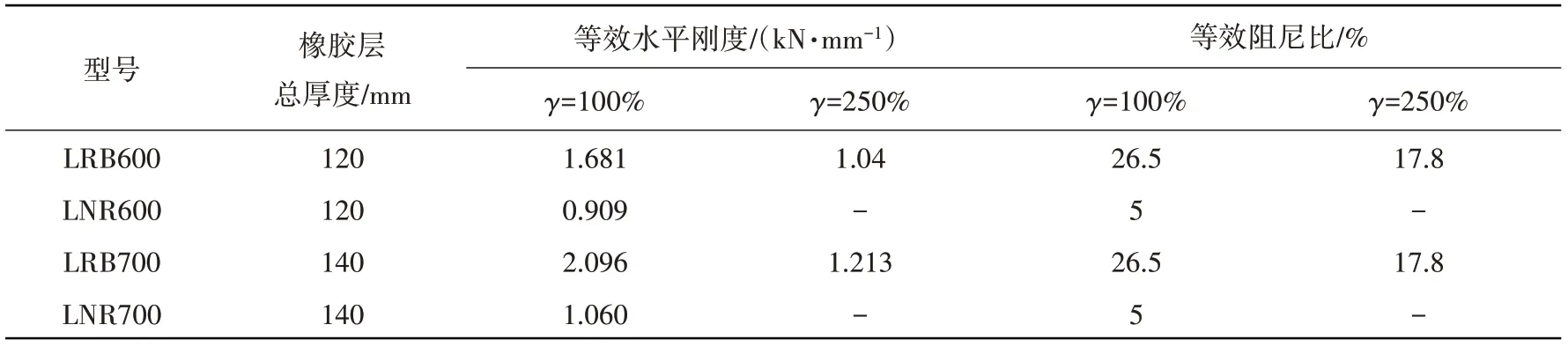
表2 隔震支座性能参数表Table 2 Seismic performance parameters of seismic isolated bearing

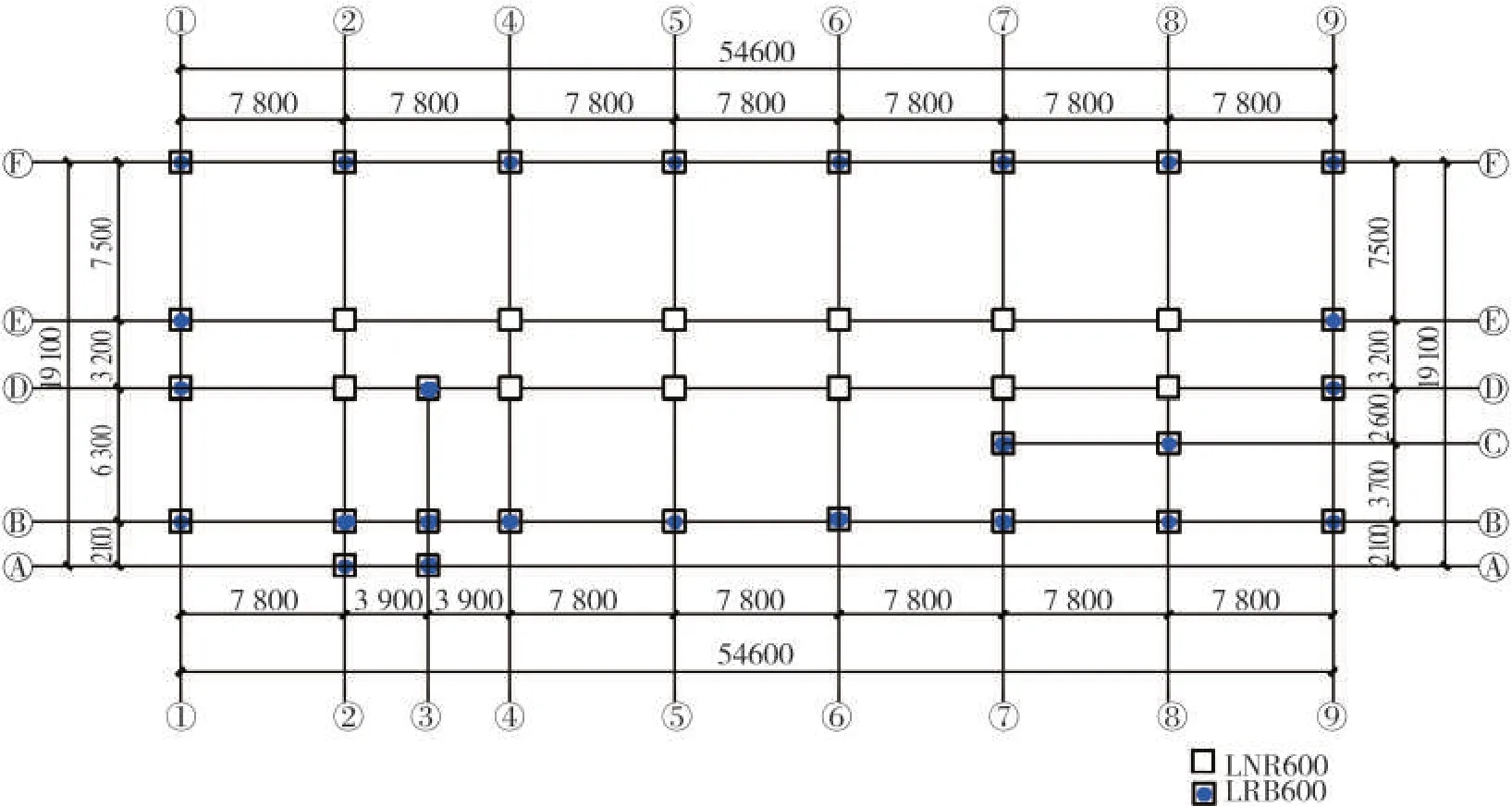
图4 原设计的隔震支座平面布置图Fig.4 Original isolated arrangement of the isolated buildings

考虑到该设计结果要与优化结果进行对比，对该设计方案代入标准人工波，并分别调整设防地震和罕遇地震下的加速度峰值为200 cm/s2和400 cm/s2，时程分析计算得到上部结构的水平向减震系数为0.4，设防地震下上部结构的最大层间位移角为1/850，小于1/400，罕遇地震下各隔震支座的最大位移224 mm，小于支座容许位移330 mm，因此，原设计的隔震支座布置方案可保证隔震结构抗震安全。但在设防地震下，设备加速度为349 cm/s2，大于设备容许加速度200 cm/s2。因此，原设计不能保证设备在地震作用下安全运行。

3.2 隔震结构-设备组合体系的优化过程及结果

3.2.1 工程优化及结果

对该工程采用隔震结构-设备组合体系的优化方法，进行隔震结构-设备组合体系的设计。

首先，该建筑为乙类建筑，各支座竖向压应力限值为12 MPa，依据各柱底的重力荷载代表值，初选得隔震支座直径为600 mm 和700 mm，且各直径的支座可以采用两种类型：LNR 和LRB。由于支座直径大于500 mm，按《建筑抗震设计规范》的要求［14］，隔震支座等效刚度和等效阻尼比取γ=100%的相关数值。这样，在所有隔震支座布置中，隔震层参数最小的情况是所有支座均为LNR600，各参数最大的情况是所有支座均为LRB700。当所有支座布置为LNR600 时，依据已有的隔震支座参数表，隔震层的等效刚度和等效阻尼比为：

kb=38 × 0.909=34.542 kN/mm，ξb=0.05

当所有支座均为LRB700时，隔震层的等效刚度和等效阻尼比为：

kb=38 × 2.096=79.648 kN/mm，ξb=0.265

因此，隔震层参数范围为：kb=[3.4542,7.9648]× 107N/m，ξb=[0.05,0.265]。

其次，设备在楼板放置时，可采用固定连接，也可简单放置其上，或采用空气弹簧、橡胶防滑垫或阻尼润滑材料等装置。通常设备与楼板固定连接采用螺栓或焊接，故连接处的阻尼比取为0.02，连接处的刚度近似为设备刚度，设备刚度ke==6.58 × 106N/m。若设备采用隔震垫等装置与楼板连接，参考《石油浮放设备隔震技术标准》（SY/T0318-98）［11］，依据设备质量13 000 kg，可选择多个硅油阻尼型隔震垫并联，则连接处的水平刚度为1.04 × 106N/m，等效阻尼比为0.15。

因此，设备参数范围为：ξe=[0.02,0.15]，ke=[1.04,6.58]× 106N/m。

目标函数为：

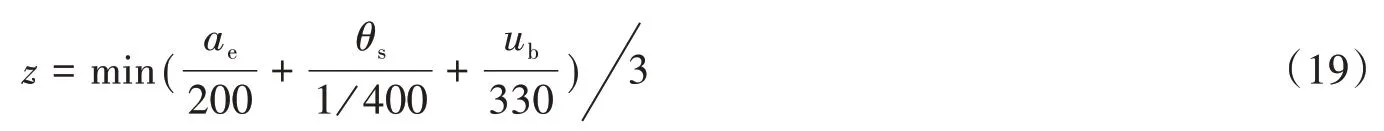
其中：由于初步选定的最大的隔震支座直径为700 mm，最小的支座直径为600 mm，umax取最小隔震支座对应的容许值，即min(0.55D,3tr)，由表2 可知：直径为600 mm 的隔震支座橡胶总厚度为120 mm，则umax=min(0.55× 600,3× 120)=330 mm。

约束条件为：

将以上模型进行MPGA优化，最终得到的隔震层和设备的最优参数为：

kb=5.782 × 107N/m；ξb=0.225；ξe=0.15；ke=4.614 × 106N/m

3.2.2 原设计方案与优化方案结果对比

表3列出了原设计方案与优化方案在设防地震下各层的最大层间位移角。

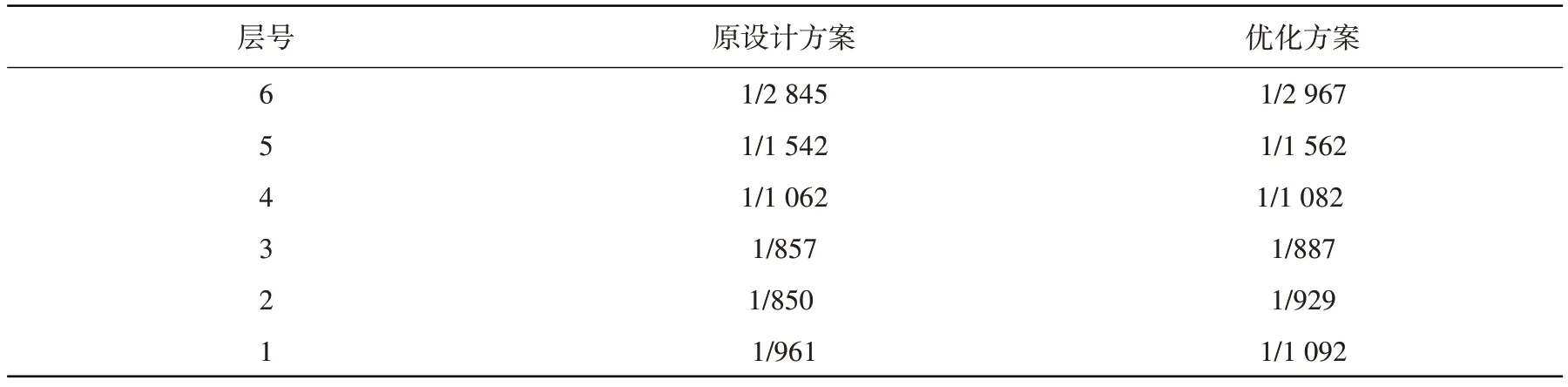
表3 优化方案与原设计方案在设防地震下的最大层间位移角Table 3 Inter-story drift ratio in the optimal and original schemes under moderate earthquake

从表3可以看出：优化方案的各层层间最大位移角均小于原设计方案，说明优化方案在设防地震下对上部结构的保护要优于原设计方案。

此外，与原设计方案相比，采用优化方案后，罕遇地震下隔震层位移由224 mm减小至175 mm，减小幅度为22%。因此，该优化方案的减震效果要优于原设计方案。

图5为设防地震下原设计方案与优化方案的设备加速度时程曲线。

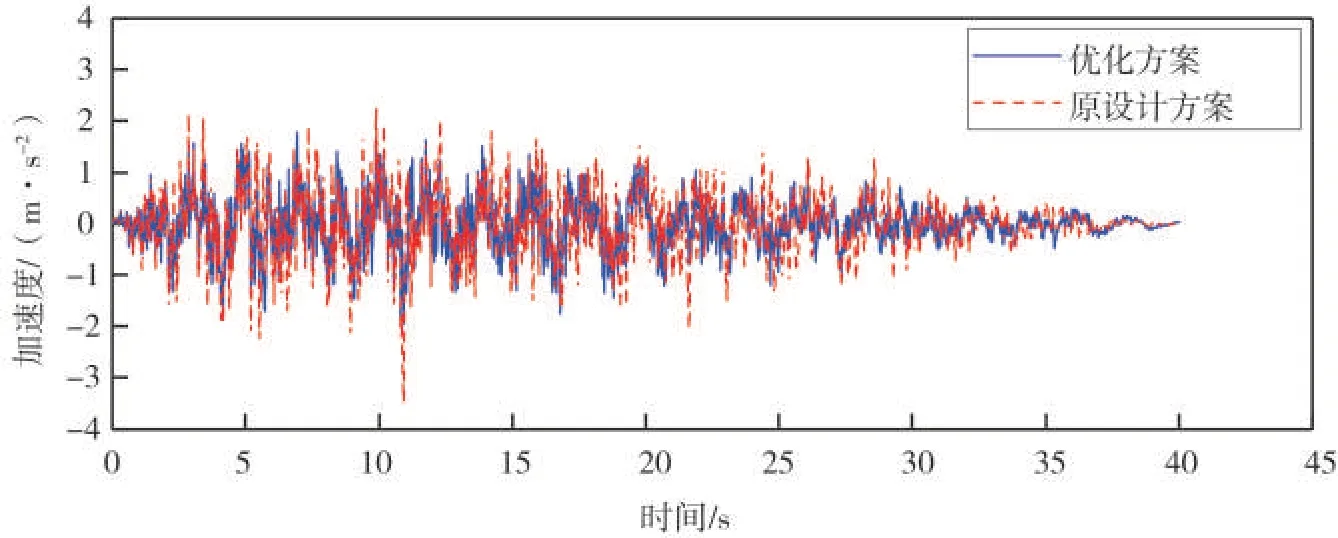
图5 设防地震下原设计方案与优化方案的设备加速度时程曲线对比Fig.5 Acceleration time history of the equipment in the optimal and original schemes under moderate earthquake

由图5 可知：原设计方案的设备峰值加速度为349 cm/s2，优化方案的设备峰值加速度仅192 cm/s2，优化方案对设备加速度的减小幅度达到45%，采用优化方案后，设备的加速度小于容许加速度200 cm/s2，说明采用该方案，除了可保证隔震结构抗震安全，还可保证设备安全。

考虑到以上结果仅为输入1条人工波得到的，为了验证该优化方案在其他地震动情况下也满足要求，按《建筑抗震设计规范》（GB50011-2010）［14］的选波要求，按建筑场地类别和设计地震分组，并满足频谱、持时和幅值的要求，在设防地震和罕遇地震情况下，分别选取5条实际强震记录和2条人工波，地震记录见表4。

表4 选择的地震波Table 4 Selection of seismic waves

将以上地震动代入优化方案并进行时程分析，并将各条地震动的分析结果进行平均，计算结果与1条人工波的结果对比，见表5。

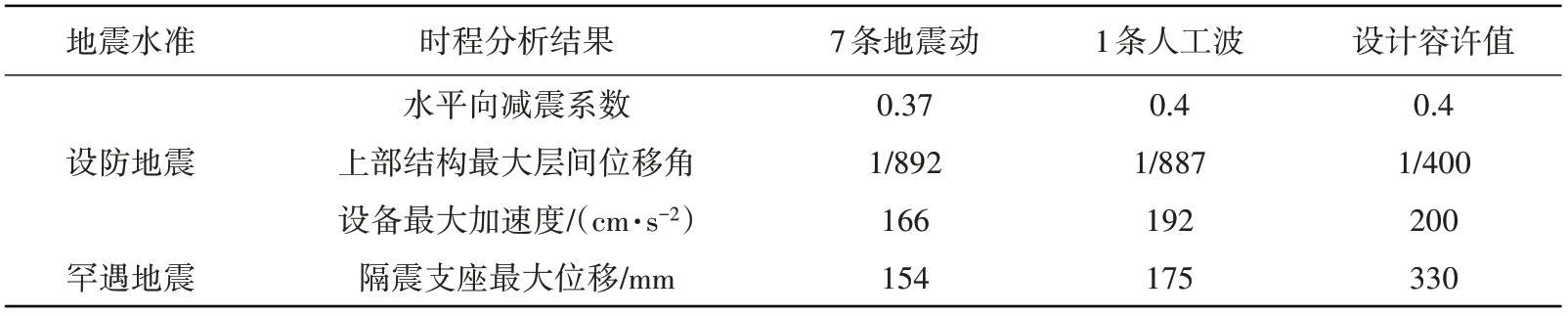
表5 人工波与7条波的结果对比Table 5 Comparison of the results between artificial wave and 7 waves

从表5可看出：7条地震动的结果均满足设计要求，并且均小于1条人工波的计算结果。

4 结论

本文考虑隔震结构与设备的非比例阻尼影响，建立了隔震结构-设备组合体系的动力分析模型，给出了基于多种群遗传算法的隔震结构-设备组合体系的优化设计方法，并用一个工程实例进行分析，得到如下结论：

（1）原设计可保证隔震结构抗震安全，但在设防地震下，设备加速度大于容许值。因此，仅考虑隔震结构的抗震安全，对于设置有重要设备的隔震结构，并不能保证设备在地震中正常运行，建筑功能不中断。

（2）采用优化方案的设备和隔震层动力参数，与原设计方案相比，设防地震下上部结构各层层间最大位移角均略有减小，设备加速度峰值减小45%，罕遇地震下隔震层位移减小22%。说明优化方案可同时使设备与隔震结构达到较好的减震效果，且可保证设备的抗震安全。