本科泛函分析课程教学思政的探讨

赵 霞

（重庆师范大学数学科学学院，重庆 401331）

1 泛函分析课程教学思政的必要性

1.1 泛函分析课程教学现状

泛函分析课程是数学专业学生的一门专业基础课程，是一个数学专业学生所必须要掌握的分析知识，这些分析知识是进一步学习其他数学专业课程的基础。这个课程逻辑性强，具有一定难度系数，学生们总认为泛函分析是一门枯燥乏味，极难理解的课程。

泛函分析课程主要以课堂教学为主，讲授过程主要以课本知识点为中心，通过对定义的讲解、引理定理的推导以及课后习题的解答完成泛函分析的教学。整个课程主要目的是使学生们学习好泛函分析这门基础课，掌握好泛函分析的基础知识以及相关结论，能够在进一步学习其他课程中应用到泛函分析知识。

1.2 泛函分析课程教学存在的问题

首先，由于泛函分析主要是由大量的定义、定理、公式组成，需要大量的逻辑推理，是一个难度系数很大的学科。其可见的应用也是对其他数学学科的抽象应用，很少具有与实际生活相结合的应用，从而使同学们对泛函分析产生了枯燥乏味，难以理解的想法。

其次，泛函分析课程课堂形式单一，上课以老师讲为主。虽然老师全身心投入讲解过程，对知识点的讲解由简入难，层层递进，推理严密，但对于学生的接受情况并不是很了解，不能保证每个学生或者大部分的学生都理解听懂老师的讲解。

再次，泛函分析课程主要以基础知识教育为主，融入的德育教育相对较少。泛函分析是一门基础性学科，表面上看都是定义，公式和定理，看似一门与思政建设毫无关系的学科，但是数学中也会蕴含一些做人做事的道理，以及一些人生观，价值观。老师需要从泛函分析的知识点以及证明方式方法中去挖掘思政元素，将基础知识教育与德育有机结合。

2 泛函分析课程教学思政建设目标

泛函分析是一门基础学科，它能够渗透到很多其他方向。在泛函分析课程的教学过程中必须发挥教师的主观能动性，润物细无声地融入思政元素，将思政与教学相融合。

2.1 增加对泛函分析课程的兴趣

教师以泛函分析的教学内容为基础，借助知识点、数学史以及数学方法等恰当地融入思政元素，激发学生的想象力与好奇心，增加学生们对泛函分析的兴趣，使教书育人贯穿课堂始终。

2.2 掌握泛函分析基础课程

通过融入思政元素，让泛函分析基础知识与人生哲理相结合，使知识点更容易接收消化；通过采取不同形式的上课方式，让学生自行去理解、总结知识点之间的关系，以及知识点与思政元素之间的联系，从而打牢知识根基。

2.3 树立正确的人生观和价值观

将泛函分析的知识点与思政元素相结合，培养学生正直诚信的品质、责任感、创新精神和爱国精神，帮助学生提高解决实际问题的能力，使学生今后能更好地融入和服务社会。

3 泛函分析课程教学思政规划方案

3.1 转化教学形式

以课堂讲授为主的形式转化为讲课和研讨相结合的上课形式。老师都自认为全身心投入讲解过程，对知识点的讲解也是由易到难、层层递进，但对于学生的接收情况并不是很了解，忽略了学生对知识点的掌握程度以及教书育人的本质。老师首先通过讲课传授知识点并进行相应的思政教育，再通过研讨让学生自行去理解总结知识点之间的关系，以及知识点与思政元素之间的联系。讲课和研讨相结合的上课形式，既能引起学生的好奇心，打牢基础知识，提高课堂教学效率，也潜移默化地进行了思想教育。

3.2 采取措施吸引学生兴趣

3.2.1 通过与已学知识的结合

泛函分析主要是将有限维空间的知识点推广到无限维空间，因此我们可以将有限维空间的例子作为引入，加强与基础课的融会贯通[1]，能够让学生产生兴趣和好奇心。比如n维欧式空间是度量空间的特殊例子，从而极限、稠密集、连续映射就可以类似的延拓到度量空间；n维欧式空间也是 Hilbert空间的特殊例子，n维欧式空间里面的内积、正交、投影也适用与Hilbert空间；有限维空间中的矩阵是有界线性算子的特例，矩阵的共轭转置对应于有界线性算子的伴随矩阵，矩阵的特征值对应于有界线性算子的谱。

3.2.2 通过数学家的故事

在泛函分析的教材中，会看到很多以名字命名的数学定理以及数学不等式，包括Hilbert空间、Young不等式、Holder不等式、Cauchy不等式、Minkowski不等式、Banach空间、Han-Banach延拓定理、Banach-Steinhaus定理、Baire纲定理等等。我们可以讲述上述数学家的生平，以及让学生们自己去调查数学家的生平并分享他们的故事，体会数学家严谨的专研精神以及他们对科学真理追求的严谨态度。

David Hilbert是天才中的天才，被誉为“数学世界的亚历山大”，也被称为“数学界的无冕之王”。以Hilbert命名的数学名词多如牛毛，有些连Hilbert本人都不知道。比如有一次，Hilbert问系里的同事“请问什么叫做Hilbert空间？”。Hilbert相信每个数学问题都能够得到解决，这一信念对数学科研工作者具有极大的鼓舞。1930年，Hilbert在接受哥尼斯堡荣誉市民称号的讲演中，再次宣称：“我们必须知道，我们必将知道。”Hilbert去世后，这句话就永远地刻在了他的墓碑上。

Augustin Louis Cauchy曾经有个绰号叫苦瓜，这是由于他平常不怎么说话，如果说话也很简短，使人摸不着头绪，像一颗苦瓜一样。Cauchy的身边朋友很少，只有一群嫉妒他聪明的人。Cauchy平时除了看 Lagrange的数学书，就是看《效法基督》这种灵修书籍，这使他又获得了一个外号，“脑筋劈哩啪啦叫的人”，简单的说，其实就是“神经病”。传说Cauchy年轻的时候，向巴黎科学院学报投稿，由于他投稿的速度非常之快，稿件也非常之多，这使得巴黎市几乎所有纸店的存货都被印刷厂抢购了，并导致了市面上纸价大涨，纸张短缺。于是巴黎科学院决定，每篇论文发表的篇幅必须以4页为限，从而Cauchy的一些长篇论文就只能改投其他国家的刊物。

3.3 融入思政的教学设计

3.3.1 通过数学史增强学生的使命感与社会责任感

利用科学家的人格魅力，以他们为榜样，通过他们的示范作用，对学生进行思政教育。通过与泛函分析内容相关的老一辈数学家例如关肇直、田方增先生等的爱国敬业致力泛函分析科研与人才培养的事例，激发学生深沉的爱国热情和浓厚的济人济事济天下的家国情怀，让学生们充分意识到作为当代青年，必须认真学习科学知识，将来为祖国的发展和繁荣富强做出应有的贡献。

田方增在中学时期就感受到中国深受帝国主义的欺凌和封建军阀的压迫，自然而然地萌发出了爱国热情，希望将来的中国能够独立自强。1935年，田方增投身参加了“一二九”爱国运动，并于次年2月积极参加了中华民族解放先锋队，将自己的青春奉献给了为抗日战争和党的事业。新中国成立之后，田方增从法国回到中国，为中国泛函分析的发展做出了积极的贡献。

关肇直在新中国诞生之际，毅然决然地放弃了取得博士研究生学位的机会，束装回国，积极投身于新中国的建设中。关肇直先生主要从事数学、系统科学以及系统科学的研究。为了发展军工和航天等事业，20世纪60年代开始，关肇直先生就投入到现代控制理论的研究，在导弹制导、潜艇控制以及人造卫星测轨等项目中作出了一系列非常重要的贡献。

3.3.2 在泛函分析知识点中挖掘思政元素

泛函分析抽象难懂，都是一些公式、引理、定理，看似与思政没有任何关系，我们需要深层次去挖掘泛函分析知识点中的思政元素，如果能够将泛函分析知识点与思政元素相结合，或许能够让学生们容易理解。下面将列举几个从泛函分析的定理以及定义中挖掘的思政元素。

定理1[4]（Hahn-Banach延拓定理）假设X是一个实的或复的线性空间，Z是X的一个子空间，p（x）是定义在X上的次线性泛函。如果f是子空间Z上的实或复的线性泛函，并且满足

那么存在f的一个延拓，其是X上线性泛函，并且满足

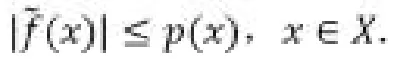
Hahn-Banach延拓定理表明一个算子只要在一个子空间上的范数能够得到控制，那么这个算子就能延拓到整个空间上，并且其范数也能够得到控制。虽然个人的影响力很小，但是几个人或者一群人的影响力可能就足以撼动世界，千万别“不以善小而不为，不以恶小而为之”。

定义2[4]（Hilbert空间）一个完备的内积空间则称为Hibert空间。

定义3[4]（Banach空间）一个完备的赋范空间则称为Banach空间。

由于不同空间的定义不一样，它们具有不同的特征，从而导致它们有不同的结论。Hilbert空间和Banach空间是两个不同的空间，满足不同的规则，Hilbert空间由于有定义内积，从而上面有正交和投影算子等，而Banach空间上没有内积的定义，不存在正交和投影算子。从而引导大家做事要有原则，要在一定的规则规矩下办事，不能越界。

定理4[4]设X是一个内积空间，M是X的完备子空间，则对每一个x∈X，存在唯一的y∈M，使得||x-y||=d(x,M)。

泛函分析中的定理都有很多条件，在这些条件下结论才成立，此定理要求M是X的一个完备子空间，如果M在X中不完备，则结论就不一定对了。虽然很多问题、项目需要同学们创新，但是在创新的情况下也需要有前提，符合规则的创新才是值得赞扬和提倡的，超出规则的创新就会被淘汰。

通过挖掘泛函分析课程知识点的思政元素，让专业教育与思政教育有机融合，既讲解了专业知识，增加了课堂的乐趣，也在潜意识中灌输了为人处世的方式方法。

3.3.3 在泛函分析证明方法中学习做人做事

泛函分析解决问题有很多方法，包括从结论出发去证明定理，根据等价定义证明结果，利用已知结果直接得出结论等。在这些方法中我们希望能够适时地融入思政教育，将一些做人做事的道理渗透到教学中。

定理5[3]设X和Y是两个赋范线性空间，T是从X到Y的线性算子，则以下条件等价

a、T将定义域中的有界集映到有界集；

b、存在常数M0，使得对一切x∈X有||Tx||M||x||；

c、T在定义域内的一点连续；

d、T在定义域内处处连续。

泛函分析中会有很多等价定义，例如定理5，赋范线性空间上的有界线性算子就具有以上四种等价定义，在证明一个算子是有界线性算子时可能直接用定义证明并不容易，但可以转化为其他等价定义来证明。因此，在生活中，一些实际问题并不是轻而易举就能解决，如果最开始的决策是错误的，事情很可能发展得越来越复杂，在这种情况下不要轻言放弃，及时改变思路，转换思想，进而化难为简。

泛函分析的定理证明可以从结论出发去寻找工具和条件，这样有目的性地解决问题才能认清问题的本质，明白条件的作用和意义。

定理6[3]假设X是一个赋范线性空间，Y是一个Banach空间，那么B(X→Y)是一个Banach空间。

证明B(X→Y)是Banach空间则需要证明其每个Cauchy序列都收敛，从而任取一个Cauchy序列{Tn}，然后得到对每一个x∈X，{Tnx}构成空间Y的一个Cauchy序列，从而可以明白条件Y是Banach空间的作用，继而完成证明。在生活中遇到问题时，我们得通过问题去寻找原因与本质，寻找到了原因才不至于再次犯错或者出现同样的问题。

泛函分析的学习过程需要总结，课本内容很多，习题也很多，老师并没有时间一一讲解，比如一些度量空间，Hilbert空间以及 Banach空间的证明，老师只能就一些例子给了证明结果，学生们需要认真总结证明过程，自己尝试对一些例子的证明，只有认真总结之后遇到类似的问题才能够利用类似方法解决，能够举一反三。凡事都要自己尝试，并不是只是眼睛看会了，在吸取别人的经验的同时，总结出一套自己解决问题的方法，这样遇到事才会游刃有余，这样才能学得活，记得牢[4]。

引理7[5]（Minkowski不等式）设，那么，并且成立不等式||f+g||p||f||p+||g||p。

泛函分析很多引理虽然其有着存在的意义，但其主要目的是为了证明某个重要定理。通过此引理能够得到p1时，按范数||·||p构成赋范空间。我们从中引导学生们要有一定的服务意识和奉献精神。

泛函分析解决问题的方法众多，很多方法都蕴含了人生哲理以及做人做事的道理，通过泛函分析解决问题的方法，挖掘其与思政建设的关系，融入思政教育。

4 结语

泛函分析是数学专业学生的一门专业必修课课，课程难度系数相对较大，趣味性弱。老师需要在泛函分析教学的过程中转换教学模式，挖掘思政元素，融入思政教育，增加学生对泛函分析课程的兴趣。让学生在掌握泛函分析基础课程知识点的同时能够学会一些做人做事道理，树立一些正确的人生观和价值观。