具有饱和发生率和恢复率的HIV模型稳定性分析*
张馨予,王丽媛
(兰州交通大学 数理学院,甘肃 兰州 730070)
0 引言
艾滋病病毒即HIV病毒主要破坏人体免疫系统,其主要攻击T淋巴细胞,并大量损伤T淋巴细胞,导致病毒入侵,使人体免疫功能遭到破坏。自文献[1]中首次引入HIV的CTL免疫反应模型,HIV模型就引起了众多研究者的关注与讨论,并建立了很多CTL免疫模型进行研究[2-10]。发生率和恢复率均是传染病动力学中不可或缺的重要因素。研究发现,饱和发生率比线性发生率更能反应出T淋巴细胞被感染后的变化趋势。2015年,文献[11]提出了带有饱和发生率的CTL免疫反应模型,即模型(1):
(1)

(2)
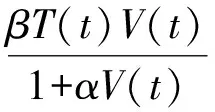
1 解的非负性和有界性
引理在初始条件T(0)>0,I(0)≥0,V(0)≥0,C(0)>0的情形下,模型(2)的解(T(t),I(t),V(t),C(t))是非负的,且始终有界。

假设存在最小的时间t2>0使得V(t2)=0,代入模型(2)的第三个方程得到
通过求解方程可以得到




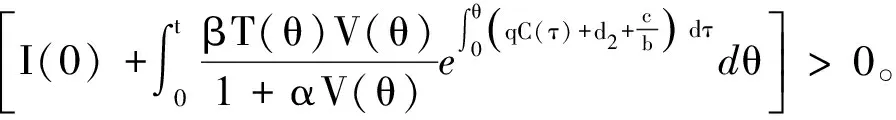
故模型(2)的解是非负的。因此,当T(0)>0,I(0)>0,V(0)>0,C(0)>0时,解是非负的。
下面证明解的有界性。令
对L(t)求导,得
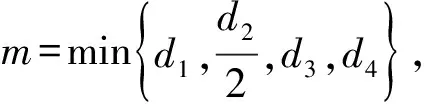
故模型(2)的解始终有界。
由模型(2)的前两个方程得

λ1-d1T(t)-d2I(t)-qI(t)C(t)=
λ1-d1T(t)-I(t)[d2-qC(t)]≤
λ1-n(T(t)+I(t)),n=min{d1,d2}。
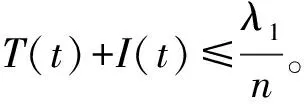
于是得
由模型(2)的第四个方程得

由引理可得模型(2)的正向不变集为
(3)
下面就在Ω里研究模型(2)的动力学性态。
2 基本再生数和平衡点
基本再生数是HIV模型中,为了刻画在发病初期疾病传染时的一个重要阈值,它表明了在一个全部都是未感染的T细胞中混入一个已感染T细胞,在其平均感染周期内所能传染的T细胞数量。
根据下一代矩阵的方法[14],得到
即有
因此,下一代矩阵为
FV-1=

将无病平衡点代入,并得到基本再生数

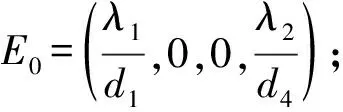
证明令
通过求解方程得到
其中V*为下面方程的正解:


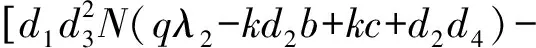
d3N2β(kλ1b-d4λ1-d4c)-(d1α+β)·
(qbλ2d3N2+d2d3d4N2b-cd3d4N2)]V*+
N2[qd1d3λ2b+d4(d1d2d3b-Nbβλ1-d1d3c)]=0。
由此可以得到V*的一元三次方程A1V*3+A2V*2+A3V*+A4=0,通过根与系数关系有


d3N2β(kλ1b-d4λ1-d4c)-(d1α+β)(qbλ2d3N2+
d2d3d4N2b-cd3d4N2)]<0,
A4=
N2[qd1d3λ2b+d4(d1d2d3b-Nbβλ1-d1d3c)]>0
。
由解的非负性可知,在域Ω中模型(2)有一个正平衡点E*。
3 稳定性分析
3.1 无病平衡点稳定性分析
定理21)若R0<1,则无病平衡点E0是局部渐近稳定的;
2)若R0>1,则无病平衡点E0是不稳定的。
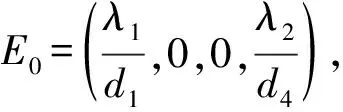
它的特征多项式为
(ω+d1)(ω+d4)·

即得
得到特征值
ω1=-d1,ω2=-d4。
由根与系数关系可得
根据Hurwitz判据可以得出,当R0<1时,所有的特征值都有负实部,当R0>1时,特征值存在一个正值。因此,结论得证。

证明设(T(t),I(t),V(t),C(t))为模型(2)满足初始条件(3)的任一正解。为方便计算,构造出正定的Lyapunov函数,
沿轨线求导得
代入λ1=d1T0,λ2=d4C0得


所以在D0中最大的不变集为

3.2 正平衡点稳定性分析
定理4若R0>1,正平衡点E*=(T*,I*,V*,C*)是全局渐近稳定的。
证明设(T(t),I(t),V(t),C(t))为模型(2)满足初始条件(3)的任一正解。为方便计算,构造正定的Lyapunov函数,
沿轨线求导得
代入
得

{(T,I,V,C)|T=T*,I=I*,V=V*,C=C*}。
基于LaSalle不变集原理,当R0>1时,正平衡点E*=(T*,I*,V*,C*)是全局渐近稳定的。
4 数值模拟
本节通过数值模拟来验证所得结果的有效性。
例1在模型(2)中取参数:λ1=40,d1=0.1,β=0.02,α=0.1,b=0.4,c=0.3,d2=2,q=0.5,N=15,d3=1,λ2=90,k=0.3,d4=0.3。经计算可得,基本再生数R0<1,所取参数满足定理3的条件,因此无病平衡点E0(400,0,0,300)为全局渐近稳定的(如图1所示)。
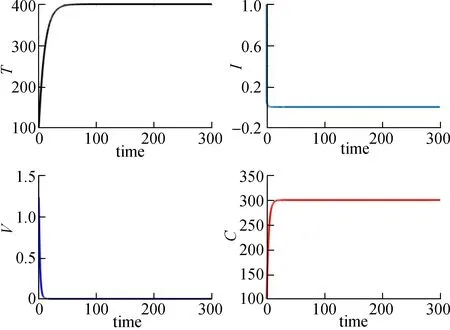
图1 无病平衡点E0稳定性的数值模拟
例2在模型(2)中取参数:λ1=200,d1=0.1,β=0.02,α=0.1,b=0.4,c=0.3,d2=2,q=0.5,N=15,d3=1,λ2=90,k=0.3,d4=0.3。经计算可得,基本再生数R0>1,所取参数满足定理4的条件,因此正平衡点E*(1 185.1,0.35,5.25,461.4)为全局渐近稳定的(如图2所示)。

图2 正平衡点E*稳定性的数值模拟
5 结语
本文提出了具有饱和发生率和饱和恢复率的HIV模型。利用Hurwitz判据和LaSalle不变集原理证得,当R0<1时,无病平衡点是局部渐近稳定的和全局渐近稳定的。通过构造正定的Lyapunov函数得,当R0>1时,正平衡点是全局渐近稳定的。讨论结果表明,虽然饱和恢复率不影响系统的动力学特性,但饱和恢复率影响基本再生数,从而影响到平衡点的全局稳定性,即加入饱和恢复率后使模型(2)的基本再生数减小,降低了T细胞被感染的风险,延缓了感染HIV的进程,并对延长患者生命和减少感染起到了积极作用。

