水面救生机器人天线耦合分析*

黄大志，徐慧丽，吕继方

(江苏海洋大学 海洋工程学院，江苏 连云港 222005)

0 引言

随着救援需求的不断发展，水面救生机器人应用越来越广泛。水面救生机器人的工作环境大多恶劣，救援工作要准确快速安全地进行，必须全程都能接收到信号且不能出现盲区，因此对于整个系统的可靠性要求较高。不同的水面情况对电磁波的反射能力不同，因此对天线的性能可能有着不同程度的影响，但总体影响较小，所以本文暂不考虑水面情况对天线的影响。随着现代社会新科技的不断发展，越来越多的电子设备搭载到面积有限的工作平台上，导致上面的天线数量增多，而这些天线有着各种不同的类型以及工作的各种频段等，使得平台上的电磁环境比较复杂。所以对于水面救生机器人平台来说，如何改善电磁兼容性是个绕不过的难题[1]。改善电磁兼容性有很多方法，本文采用对天线位置进行分析的方法来降低天线间的耦合度[2]。

电磁兼容在车载、机载等天线[3]上应用的案例比较丰富，研究者在研究如何使用天线的问题上常常使用数值仿真技术。越来越多的国内外学者研究复杂电磁环境中的电磁兼容性问题。文献[4]在分析民用飞机的天线布局时提出可以使用矩量法，文献[5]利用时域有限差分法，文献[6]从场的角度运用矩量法和时域有限差分法混合法，对多根天线在车辆上的电磁兼容性问题进行研究。关于水面救生机器人天线问题的研究相对较少，但是对于水面救生机器人同样也存在类似的问题，当多根天线作用时，天线与天线之间会相互影响，故而达不到想要的天线作用效果[7]。研究车载天线电磁兼容问题多使用广义S参数理论[8]，本文采用正在研究实验的产品并参考S参数理论，分析水面救生机器人天线间的耦合度，以期对布局水面救生机器人天线工作提供参考。

1 模型建立与分析

以水面救生机器人天线间的电磁兼容为对象，分析天线间的电磁耦合度。首先使用Solidworks软件画出简化后的水面救生机器人模型，尺寸约为1 165 mm×873 mm×280 mm，将得到的水面救生机器人简化模型导入到CST软件中，并在机器人上画出天线的模型，如图1所示。

图1 水面救生机器人三维简化模型

被救援人员要依附在小型尺寸的水面救生机器人上，对于天线的设计尺寸要尽可能小。设计频段为2～4 GHz的鞭状天线，半径为0.4 mm,长度为23 mm。由于水面救生机器人壳体以及内部器件会对天线产生影响，为了体现该影响将鞭状天线模型放置于有限大尺寸的理想导电平面上。如图2所示，导体平面尺寸取与水面救生机器人中心凹陷尺寸相近的矩形平面100 mm×100 mm，天线底端距离该平面0.5/2 mm。另外，天线的放置位置、天线的数量等都会对天线产生一定的影响[9]，通过仿真分析对比天线在上述情况下的天线图情况，为后续研究天线的耦合度提供参考。

图2 理想情况下鞭状天线模型

天线间的电磁耦合是指两副或两副以上的天线之间存在互感，使得天线间的电磁能量变化相互影响[10-12]。如图3所示，当接收天线接收到发射天线发射的电磁波时，两副天线之间会产生电磁耦合。通常用耦合度来表示：

图3 天线耦合示意图

(1)

即接收天线端口的净输出功率与发射天线端口的净输入功率之比。式中，C(dB)为天线间电磁耦合度；Pout为接收天线的净输出功率；Pin为发射天线的净输入功率。

如图4所示，根据微波网络知识，两副天线(收发天线)系统(见图3)可以等效为二端口网络。发射天线连接在端口1处，接收天线连接在端口2处，此时端口2处的天线有着网络匹配的状态。

图4 二端口等效网络

由图4可知，二端口网络的S参数矩阵为

(2)

端口2的输出功率为

(3)

端口1的输入功率为

(4)

由于端口2处于阻抗匹配状态，则

(5)

(6)

当端口1也匹配时，S11=0,由此可得天线间的耦合度为

C=10log(|S21|2)。

(7)

2 仿真结果与讨论

2.1 天线的放置位置、天线的数量对天线的影响

2.1.1 天线放置位置的影响 选取导电平面尺寸长为100 mm，宽为100 mm，材料选择理想导体材料PEC。如图2所示，首先将天线放置于导体平面的中间然后进行仿真分析。图5为天线放于平面中间3 GHz时E面、H面的方向图。当频率为3 GHz时，波长λ=100 mm，与导电平面尺寸相等，由于导电平面的长宽也相等，所以天线的能量基本不会沿着平面向下辐射，且沿x轴和y轴辐射的能量也大致相等，对天线的耦合程度也差不多。

a E面方向图

图6为天线分别在2.6，2.8，3.0,3.2,3.4 GHz时phi=0°的二维方向图。天线频率越高，波长越长，3.2 GHz和3.4 GHz时，此时波长大于导电平面尺寸，部分能量会辐射到导电平面之外，方向图的后瓣也开始增多，频率越高，后瓣会越多。

图6 phi=0°时天线二维方向图

图7为天线放置在导电平面边缘处的模型图。将天线放在平面的边角处(x轴和y轴的正半轴方向)，且与x轴、y轴导电平面的边缘距离均为10 mm。

图7 天线置于导电平面边缘处模型

图8为天线放置在导电平面边缘频率在3 GHz时的天线方向图。此时边缘天线的辐射将产生很大的变化。从图8a放置在边缘的三维图可以看出，导电平面对天线的辐射更集中在x轴的负半轴方向和y轴的负半轴方向，而靠近边缘的能量会向下辐射。因此从图8b可以看出存在很大后瓣[13]。

a 三维方向图

2.1.2 天线数量的影响 由于实际工程中均不止一副天线，所以分析多副天线的情况。上述分析了一副天线置于导电平面x轴y轴正半轴的天线情况，现将同样一副天线置于x轴负半轴、y轴正半轴方向，如图9所示。此时两副天线1#和2#关于yoz面对称，距离为80 mm。

图9 天线模型示意图

图10为1#天线在2～4 GHz频段最大增益曲线图。图10a为一副天线置于导电平面右上侧边缘时的最大增益曲线图，图10b为两副天线置于导电平面边缘时右上侧天线的最大增益曲线图。可以看出两副天线最大增益略大于只有一副的情况，所以当放置多副同种天线时，其最大增益会因为多副天线间的耦合作用而增加。

a 一副天线置于导电平面边缘时

通过上述分析，天线放置位置和天线数量等都对天线性能产生影响。位置不同时，天线方向图会有所变化；天线数量增加时，天线的最大增益会因为耦合作用而增加。

2.2 理想导体平面上收发天线的电磁耦合度

根据前述取两副同样的鞭状天线工作频率为2～4 GHz，同样将它们放在理想导体平面上，同时天线的结构尺寸与导体平面尺寸不变，上述1#天线和2#天线之间的距离为80 mm，现改变两根天线之间的距离，距离为x(如图11所示)，然后进行参数扫描，仿真得到如图12所示的天线间的耦合度。

图11 天线模型示意图

从图12可以看出，天线之间的距离与耦合度成反比，即随着两副天线之间的距离逐步减小，天线间的电磁耦合度增加。当1#天线与2#天线距离x≥40 mm时，在2～4 GHz天线间的电磁耦合度均小于-10 dB;当x一定时，在同一频段内，随着天线工作频率的变化，天线间的电磁耦合度呈非线性变化趋势，所以可以选择不同的工作频率来调整天线间的电磁耦合度[14]。

图12 理想导体平面上天线的电磁耦合度

2.3 水面救生机器人上收发天线的电磁耦合度

如图11所示，将相同两副天线放置在水面救生机器人上，开始时1#天线和2#天线之间的距离为80 mm。现改变两根天线之间的距离，同样距离为x，仿真得到如图13所示天线间的耦合度。

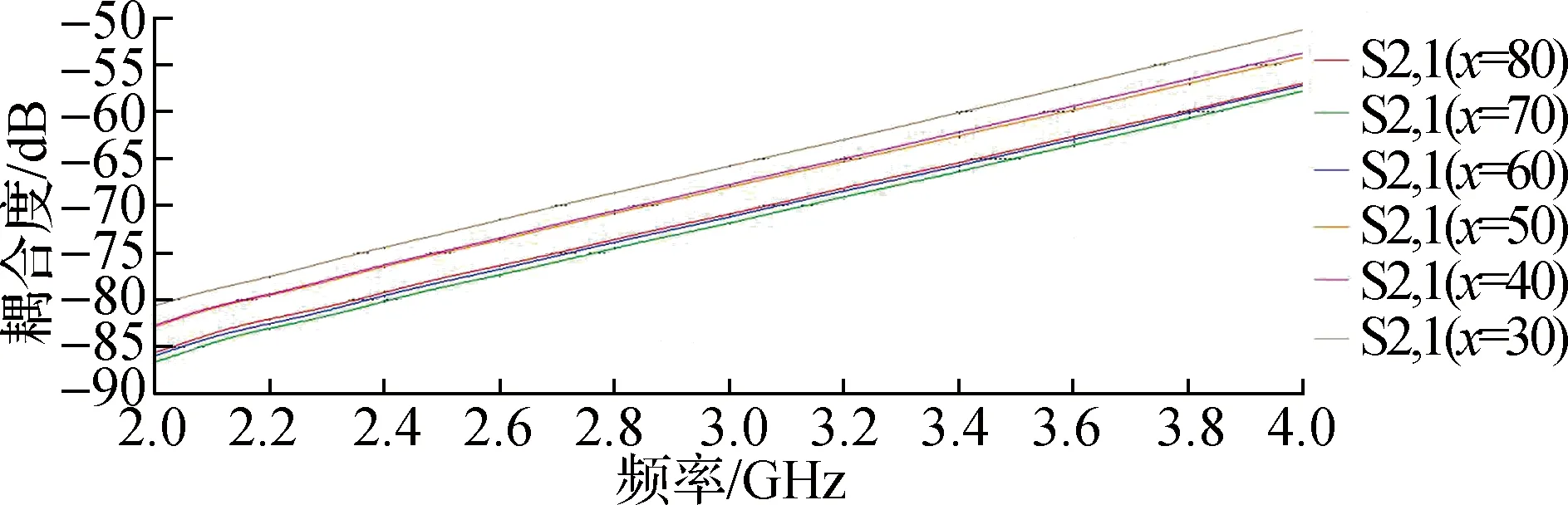
图13 水面救生机器人天线的电磁耦合度

从图13可以看出，总的趋势依旧是随着两副天线之间的距离逐步减小，天线间的电磁耦合度增加。当两副天线距离为70 mm时，此时耦合度达到最小。与图12对比可知，天线放置在水面救生机器人上时，由于水面救生机器人的材料相对介电常数较小，所以天线间的耦合度呈下降趋势。因此可知该水面救生机器人的材料对天线间耦合度的影响较小，所以对于后续水面救生机器人天线布局时，可只考虑天线间的耦合度关系。

最后根据天线本身的性能及上述仿真结果总结天线的设置参数以及放置位置：采用两副频段为2～4 GHz，半径为0.4 mm、长度为23 mm的天线，考虑到后续其他天线的布局，初步将此鞭状天线放置在水面救生机器人的边缘处。

3 结论

本文建立了水面救生机器人以及该机器人上天线的模型，然后根据S参数理论，得出接收天线和发射天线之间的电磁耦合度方程。利用CST仿真软件分析了天线放置在不同位置、天线的数量对天线方向图、增益等的影响，同时根据前面分析结果又分析了理想导体平面上天线的耦合度。结果表明，天线的放置位置、天线数量都对天线的方向图、增益等产生一定的影响以及天线间的耦合度随着天线的间距增大有减小的趋势。本文的建模过程与最后得到的结果，可为后续水面救生机器人天线的电磁兼容分析提供参考。