线性扰动条件下饱和土体扩张计算分析

张 泽，焦永刚，任永忠

( 1. 甘肃建投土木工程建设集团有限责任公司，甘肃 兰州 730070；2. 兰州工业学院 土木工程学院，甘肃 兰州 730050)

柱孔扩张原理被广泛应用于岩土工程中，该理论的提出能够解决沉桩、隧道工程及静力触探等问题。该理论模型较好的反映和帮助解决了一些岩土工程问题，与实际对象较为符合。岩土工程中小孔扩张理论最早由Vesic[1]提出，并进行了相关的试验验证。土体与连续介质有着非常大的差异，一方面散体性质使得描述土体破坏的强度理论与连续介质有着较大的区别，需要体现出土体之间的摩擦效应，因此Mohr-Coulomb在岩土工程中得到较多的应用；另一方面，土体的多相性，使得土体孔隙之间充满水，在外部荷载作用下其力学相应相比于固体介质要更加复杂，需要考虑到孔隙水压力的变化。岩土工程中的小孔扩张更为复杂，但受实际需求的牵引，这一问题得到了众多研究人员的广泛关注。李雨浓[2]等学者采用Tresca准则分析了扩张压力与扩底半径之间的关系，并提出了通过半径来判定土体应力状态的公式。邱敏[3]借助旁压试验去分析对比了3种小孔扩张理论下不排水强度结果，指出超固结比对粘土不排水强度的估算有影响，处于重度超固结的黏土，利用传统方法和有限元方法计算的结果较为接近。郑金辉[4]在扩张理论中引入了土体的破碎程度及剪胀特性，高初始应力会影响扩张过程中孔周土体的应力状态，对于土体屈服有着较大的影响。土体的各向异性特性以及应力历史均会对扩张过程中的应力分布及应力状态产生影响，并且对极限扩张压力的影响最为明显[5]。工程中沉桩过程会对孔壁土体产生扰动，导致土体自身的结构性产生变化，土体强度降低[6]。超孔隙水压力对于土体强度的影响较大，扩张过程中人们更为关心的是超孔隙水压力的大小与分布[7-11]。

目前，已有的研究成果推动了扩张理论的发展，为实际工程以及理论研究发展起到了积极作用。然而，软土中由于过高的含水率(接近于饱和状态)和较低的渗透性，使得扩张时模型基本不排水，采用不排水强度更为合理，此时Mohr-Coulomb屈服准则退化为Tresca准则，研究饱和软黏土扩张后超孔隙水压力的分布对于工程建设具有较强的实际意义。与此同时软土强度低，土颗粒结构易损性较强，极易受到外部施工扰动而导致土体强度发生变化，已有的研究并未考虑到外部扰动对土体强度的影响，使得应力状态会被高估，不利于工程安全。因此，在理论模型中引入扰动因素是十分必要的。本文基于经典Vesic理论，进行了不排水条件下饱和黏性土体的扩张研究，在计算中引入了扰动系数，使得扰动在塑性区范围内被定量化描述，基于扰动程度的线性模型，推导了该条件下的扩张过程，分析给出了对应的超孔隙水压力分布规律。

1 模型的建立

1.1 土体扰动影响的量化

在沉桩施工等过程中，机械器具的成孔以及构件产生的挤压效果均会对土体产生扰动。土体属于散体材料，颗粒之间的接触所形成的结构对于土体的物理、力学性质有着强烈的影响，扰动的产生必定会导致结构发生变化，进而使得土体的强度降低，如果不考虑这一影响，采用原始土体强度进行扩张计算，得到的结果对后期施工会带来很大的风险，不利于工程建设的安全。扩张过程中，由于应力分布的特性使得土体会产生明显的弹塑性分界面，越接近孔壁受到外部荷载的影响越大，应力幅值越高，距离孔壁越近的地方越先达到屈服状态。因此，考虑外部因素的扰动时本质上就是考虑对土体强度的影响，该扰动的影响只在塑性区内产生，越靠近扰动源强度损失程度越大，随着距离的增大扰动程度逐渐降低；而当处于弹塑性交界面处时，土体的强度应当恢复到扰动前的状态，塑性区以外由于土体应力状态处于弹性阶段，因此扰动不会对弹性区产生影响。

基于对扰动的上述分析，若取系数β为扰动程度，取值范围为[0,1]。β=0时表示此时扰动程度为0，而当β=1时则表示扰动程度达到最大，强度损失为100%。由于扰动带来的强度损失仅发生在塑性区阶段，可以在塑性区内进行线性插值，从而获得不同位置处扰动后的强度，土体扰动前原始强度记作τ0，塑性区内不同位置处的强度τ′通过式(1)计算。

(1)

式中：τ′为扰动后的强度；r为径向坐标；r0为孔壁处坐标；rp为塑性区半径。

1.2 弹性阶段计算

当土体处于弹性阶段时，满足弹性力学的基本方程[12]，其中平衡微分方程如式(2)，即

(2)

式中：σr为土体径向应力；σθ为土体环向应力；r为径向坐标。几何方程满足式(3)，以压为正有

(3)

式中：εr和εθ分别表示径向应变和环向应变；ur表示径向位移。

由于分析对象为轴对称模型，因此物理量与环向坐标θ无关，由几何方程可以得到应变表达的相容方程如式(4)，即

(4)

而物理方程仍然满足胡克定律，即

(5)

式中：E为土体弹性模量；μ为土体的泊松比。

将物理方程(5)代入式(4)，得到应力分量表示的相容方程，再结合平衡微分方程式(2)，得到弹性阶段关于应力分量的控制方程，即

(6)

在孔壁处r=r0，径向应力等于内压p，有σr=p；在r→∞处，内压影响趋近于0，此时径向应力为0。通过上述边界条件得到弹性区的应力解答式(7)，即

(7)

弹性状态下径向位移为式(8)，即

(8)

1.3 扰动条件下塑性阶段计算

随着内压p的增大，孔壁处的土体由于应力幅值最大，最先进入塑性阶段。对于饱和黏土而言，由于渗透性较差，孔隙水难以在短时间内排出，因此，采用不排水抗剪强度指标进行描述较为合理，即Mohr-Coulomb准则退化为Tresca准则，如式(9),即

(9)

随着内压的增大，模型中必定会首次出现屈服状态，并且孔壁处土体最先屈服，若记此时对应的内压为弹性极限扩张压力pe，由于该位置处于弹塑性临界状态，既满足弹性理论又满足塑性理论，由弹性应力解答式(7)结合屈服准则式(9)，得到

pe=Cu,

(10)

由此可知，只要径向应力达到土体的不排水强度，那么该位置就处于临界状态，即弹塑性交界面处满足该规律。

当扩张压力p继续增大，达到一个极限值，记此时为极限扩张压力pu。塑性区内土体满足屈服准则和平衡微分方程，由此得到塑性区内土体的应力解答如式(11)，即

(11)

此时极限扩张压力pu还是未知的，前述已经指出在临界状态时，径向应力必定等于土体不排水强度，在塑性区半径rp处同样成立，利用式(10)和前述的临界状态关系，可以得到求pu的表达式，即

(12)

由此，得到塑性区内土体的应力解答为

(13)

2 孔隙水压力分布计算

扩张过程中内压的作用，会使得土体产生超孔隙水压力，Henkel孔隙水压力理论指出超孔压的大小与土体的八面体应力之间有关系，满足如下关系式:

Δu=BΔσoct+αfΔτoct,

(14)

式中：B为Skempton 孔隙水压力系数，对饱和土而言，该系数为1；αf为 Henkel孔隙水压力系数，满足αf=0.707(3Af-1)，其中Af为土体破坏时的 Skempton 孔隙水压力系数，正常固结土在 0.5～1.0 之间。

平面应变问题中，在平面外方向应力分量并不为0，因此，在计算应力张量时需要将其包括在内，并且在不排水条件下，土体的泊松比为0.5，由此得到平面外的应力分量为σz=0.5(σr+σθ)。进而得到八面体应力，即

(15)

八面体剪应力为

(16)

将塑性区应力分量代入到式(15)和式(16)后得到塑性区内土体超孔隙水压力为

(17)

3 算例分析

前述内容给出了线性扰动模型下扩张后的应力解答以及产生的超孔隙水压力，为验证理论计算的合理性，进行算例的演示计算。计算模型中土体的弹性模量为1 500 kPa，Skempton孔压系数Af为2/3，扩张后小孔半径为0.1 m，土体未扰动前原始的不排水强度为15 kPa，扰动系数β分别取0.0、0.3、0.6、1.0。结合极限扩张压力及应力、超孔隙水压力的计算公式，将参数代入后得到算例的应力、孔压分布规律。

表1 极限扩张压力结果

不同扰动系数下径向应力的分布情况如图1所示，当β=0时，即为经典的Vesic理论结果，随着扰动程度的增大，径向应力幅值呈降低规律，扰动仅在塑性区范围内，因此弹性区应力是完全一致的，应力极值出现在孔壁处，分别达到67.598、57.513、47.428、33.981 kPa。土体强度损失越大，土体所能承受的极限扩张压力越小，则应力幅值必定也越小。

图1 径向应力分布曲线

超孔隙水压力是由外部附加荷载所引发的，塑性区内超孔隙水压力随着距孔壁的距离的增大而降低，塑性区内的超孔压变化速率要大于弹性区的。不同扰动系数下扩张结束时超孔隙水压力变化如图2所示。

图2 超孔隙水压力分布曲线

附加应力引起的超孔隙水水压力由Henkel理论进行描述，Af为Skempton孔压系数，不同的值会导致八面体剪应力的权重不同，从而导致超孔隙水压力分布产生变化。当不考虑扰动影响时，随着Af的增大，超孔压幅值是逐渐增大的，距离孔壁处越远，超孔压偏差越小，并且在弹塑性交界处超孔压偏差幅度最大。图3为扰动程度为1.0时，不同Af下超孔压的分布，与图4对比可以发现扰动程度越大，随着Af取值的增大，孔压增大幅度要大于不考虑扰动影响的结果，在弹塑性交界处最明显。总体上，八面体剪应力贡献越小，扩张后超孔隙水压力幅值越小。

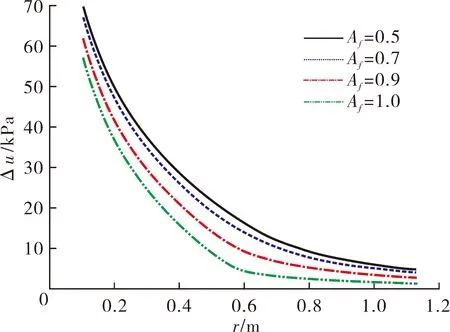
图3 不同Af取值下超孔隙水压力分布曲线(β=0.0)

图4 不同Af取值下超孔隙水压力分布曲线(β=1.0)

4 结论

1) 外部作用对土体的扰动主要体现为土体强度，因此，扩张时主要变化应限制在塑性区内，损伤系数的引入能够在塑性区进行插值从而反映出不同位置处的强度损失程度。

2) 考虑土体扰动的影响，扩张过程中极限扩张压力是要低于不考虑扰动情况下的，同时产生的超孔隙水压力值也随之降低。超孔隙水水压力随Skempton系数的增大而增大，偏差在弹塑性交界面处最明显。