细节保留目标下的自适应非局部均值图像降噪算法

於 平

(滁州城市职业学院 公共教学部， 安徽 滁州 239000)

在科学技术迅速发展的时代背景下，人们对图像质量提出了更高要求。由于图像在采集环节和传输环节皆容易受到多种因素干扰，为了得到高质量图像，采取降噪处理势在必行[1]。该处理方法是在保留图像细节的基础上，最大限度地去除图像中多余的噪声。目前，应用比较多的图像降噪方法有变换阈去噪法、空间阈去噪法等[2]。这些方法虽然可以去除一些噪声，但是对图像的原有细节影响较大，处理过程中会丢失部分图像细节信息，未能达到预期的图像处理效果[3]。另外，还有些研究学者提出采用小波变换等去噪方法，这些方法仅能够得到图像的集合特征，无法得到高质量图像[4-5]。为了弥补以往研究的不足，本文尝试提出了一种非局部均值NLM图像降噪方法与模糊边缘补足图像修正算法(FEC)结合的FEC-NLM算法。

1 图像降噪基本原理

1.1 非局部均值图像降噪

均值去噪图像处理方法与本文应用的NLM图像降噪方法相似，前者是取图像所有相似点，采取加和处理，而后求取平均值，从而达到降噪目的[6]。本文应用的NLM降噪方法是通过寻找相似像素点，为这些点赋予权重，最终达到降噪的目的。

假设噪声图像为φ，与之对应的像素点为φ(i)，求解φ(i)的非均值平均估计的计算公式如式(1)，即

NL[φ(i)]=∑j∈Ω(i)λ(i,j)φ(j)，

(1)

式中：λ(i,j)代表针对像素点φ(i)赋予的权重；Ω(i)代表以i为中心的搜索区域。其中，权重的赋予主要取决于2个像素点j和i，根据两者的相似性确定取值范围[0,1]，存在关系∑jλ(i,j)=1成立。以像素点i为中心，分割图像块，规格为λ×λ，记为Ni。同样的，以像素点j为中心，分割图像块，规格为λ×λ，记为Nj。通过求解两个分割块高斯加权欧式距离，确定像素点j、i的相似性。其中，涉及到的计算公式如式(2)，即

(2)

关于权重λ(i,j)的计算公式如式(3)，即

(3)

式中：Ga代表高斯核；h代表相似权重参数，该项参数的大小决定了图像平滑程度。其中，Ga在本算法中的作用是图像平滑度的预处理，以图像块相似度度量影响作为处理对象，去除与之对应的噪声，从而使得图像块的相似性度量精度得以提升。

1.2 模糊边缘补足图像修正处理

考虑到图像在降噪处理过程中可能存在部分图像丢失的情况，导致图像精准度下降。为了弥补这些降噪算法的不足，本文提出一种模糊边缘补足图像修正处理FEC算法。该方法建立在文献[7]的研究基础上，通过处理各个像素点，实现图像的修正。像素点处理计算如公式(4)，即

(4)

式中：μij代表图像像素点；U代表图像像素的最大值；i代表像素横坐标；j代表像素纵坐标。

确定中心点，而后取固定大小的窗口，按照FEC作业原理，对窗口中的像素采取锐化处理。按照该处理方法，取2个中心点，分别为像素点i、j，取固定大小的窗口λ×λ，窗口记为Q，对窗口Q采取锐化处理，计算公式如式(5)，即

(5)

式中：(x,y)代表位于窗口图像P内的像素坐标；λ与τ均代表缩放因子。

2 基于细节保留的自适应非局部均值图像降噪算法

以往提出的图像降噪算法在细节纹理保持方面薄弱，容易受噪声影响。所以，本文尝试修正相似图像块的权重，使得相似像素的权重得以提升。在此期间不相似像素的权重就会削弱，有助于图像块准确性的提高。

2.1 FEC处理下的降噪图像相似性权重

以往提出的NLM图像降噪方法，其作业原理是通过计算高斯加权欧式距离，根据计算结果采取相应图像处理，以此降低噪声对图像度量的影响。然而该处理方法应用期间伴随着纹理信息的平滑问题，导致图像细节未能被保留。为了弥补该降噪方法存在的不足，文献[8]提出一种非局部全变分的降噪方法(STNL)。该方法对非局部信息进行了优化，优化工具为结构张量相似性权重，以此保护边缘轮廓信息。另外，考虑到该方法的细节纹理信息保持能力不是很高,特别是噪声对结构张量造成的影响可能性较大，所以仍需要对STNL生成的图像进行修正。为此，本研究选取FEC方法作为研究工具，对图像块权重采取修正处理，使得图像相似像素权重得以提升，同时减小图像中不相似像素权重。经此算法处理产生的图像质量将有所提升，为图像纹理信息的保护给予保障。通过仿真测试可知，FEC方法能够检测到图像的纹理和边缘，操作期间不容易遭受各种因素的干扰。

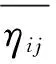
2.2 降噪图像相似性权重参数

1.1节的公式(2)中，h为相似权重参数，该参数属于常量，各个像素点赋予权重容易受此参数影响，导致图像降噪出现平滑问题。其中，h数值与平滑问题的严重性呈现正相关关系。为了避免图像边缘区域出现过大的平滑问题而降低图像质量，建议为h赋予较小值，对相似性权重参数采取以下处理。

定义相似性权重参数为h(i)，计算公式如式(6)，即

h(i)=ασ,

(6)

式中：σ参数数值取决于含噪图像噪声水平估计结果；α参数数值取决于图像内容。

2.1小节中提及的特征图像He有效处理了图像边缘纹理细节问题，所以本优化方案只需要在图像He基础上，采用像素映射方法，将He映射到区间[0,1]内，得到式(7)所求得的图像，即

(7)

式中：Ωe代表FEC图像去噪方法应用下的图像特征。为了有效区分图像内容，选取各个图像像素均值作为区分指标，Hηij可通过式(8)求得，即

(8)

式中：S代表搜索区域，该区域的中心为Hηij。

为eij设定数值区间，在不同区间下取值为α(Hηij)。其中，纹理区域赋予α(Hηij)中间值，平坦区域赋予α(Hηij)较大值，内容丰富区域赋予α(Hηij)最小值。按照上述方法，对相似性权重参数h采取修正处理，而后对修正后的图像噪声水平进行评估，评估计算方式如式(9)，即

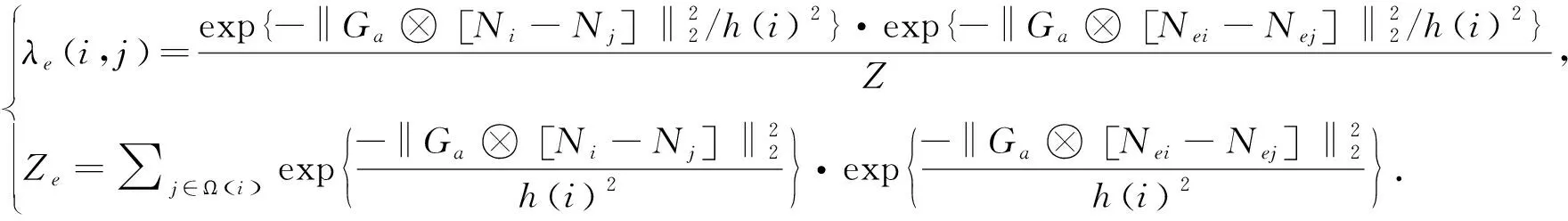
(9)

由此，本文提出的自适应非局部均值图像降噪算法可以用公式(10)来定义，即

NL[φ(i)]=∑j∈Ω(i)λ(i,j)φ(j).

(10)

2.3 降噪算法流程

第一步：图像信息初始化。将噪声图像读入算法中，开始对参数采取初始化处理。

第二步：对图像中的噪声水平进行评估。

第三步：取具有边缘纹理特征的图像。运用FEC算法对此部分图像加以降噪处理。

第四步：运用式(9)计算λe(i,j)数值。

第五步：运用式(10)计算降噪后的图像像素值。

第六步：按照步骤四和五的处理方法，循环计算各个像素点，从而得到完整的高质量图像。

3 实验测试分析

为检验本文所提FEC-NLM降噪方法的可靠性，选取5张图片作为测试对象，每一张图像的噪音不同。σ为高斯白噪声，设置2组不同参数下的高斯白噪声加入条件，运用不同降噪算法来处理这5张图片，统计图像去噪后的峰值信噪比，如表1所示。

表1 图像去噪后的峰值信噪比统计结果

表1中，σ=10条件下，FEC-NLM algorithm和STNL algorithm作用在Boat图片上的降噪处理效果相近，前者略显优势。与其他几种降噪算法相比，FEC-NLM的降噪优势较为突出；σ=20条件下，FEC-NLM algorithm和STNL algorithm作用在House图片上的降噪处理效果相近，前者略显优势，同样与其他几种降噪算法相比的优势更为显著。因此，本文所提的FEC-NLM图像降噪处理算法更为可靠，降噪处理图像效果如图1所示。

由图1可知，去噪前图像中花朵部分杂质较多、花蕊的细节表达不清晰、花瓣边缘分布大量明显的锯齿，不但影响观感而且容易传递有误图像信息，叶片图像也存在同类问题。基于FEC-NLM法去噪后，花朵的花蕊部分信息表达更加清晰，花蕊明暗变化显著、花瓣层次错落有致，立体感凸显；去噪后右图叶片上的细小破洞清晰的表达出来，叶片的杂质基本消失，由此可见，本文所提方法的去噪效果较为理想。

(a) 去噪前

4 结语

本文围绕图像降噪问题展开探究，在以往图像降噪算法的基础上，尽可能保留图像细节，对边缘纹理细节给予特殊处理，同时修正相似性权重参数h，形成FEC-NLM算法。以NLTV、NLM、STNL作为对照组，进行图像降噪算法测试对比分析。测试结果表明，FEC-NLM算法在不同高斯白噪声的影响条件下，皆可得到最好的图像降噪处理效果。