集成分区耦合策略的物理信息神经网络模拟共轭传热过程研究
陆至彬,李依梦,何畅,张冰剑,陈清林,潘明
(1 中山大学材料科学与工程学院,广东 广州 510006; 2 广东省石化过程节能工程技术研究中心,广东 广州 510006;3工数科技(广州)有限公司,广东 广州 510530)
引 言
热传递过程是自然界和工业界中普遍存在的基本现象,精确地构建其传热模型是设计高效率、低成本换热设备的关键步骤之一。在换热设备内部,热交换主要发生在气/液-固交界面,这种流体传热与固体导热相耦合的现象称为共轭传热。共轭传热过程机理可以通过控制方程(包括质量、动量和能量守恒方程)进行数学描述,通常表现为高度非线性的偏微分方程组(partial differential equations, PDE)。在实际应用中,PDE 往往难以直接解析求解,通常需要利用基于网格离散化的数值计算(如有限元法、有限差分法和有限体积法等)将计算域分散为有限个以节点连接的网格单元,并借助计算流体动力学(computational fluid dynamics,CFD)工具来获得节点处的数值解或近似解[1]。这时,网格的数量会同时影响数值计算结果的准确性和计算负荷,需要在保证计算准确性的前提下,对网格数量和计算负荷进行权衡。而实践中,某些新型换热设备具有复杂的几何形状,使共轭传热的数值模拟极为困难。同时,由于方程的高度耦合和非线性,数值模型很难与模块化流程仿真模型或数学规划模型直接集成,限制了数值模拟在实时预测、参数分析或优化设计等方向的应用。
随着数据和计算资源的爆炸式增长,深度学习在计算机视觉和自然语言处理等方面取得显著的成功[2]。人工智能领域学者将深度学习与科学计算结合,通过函数逼近理论的研究证明深度神经网络(deep neural networks, DNN)可作为通用的函数逼近工具,用于逼近任何连续函数及其导数[3]。得益于自动微分[4-5]技术的进步,理论上可以利用DNN 来近似逼近任意PDE 的解析解[6],最终替代传统的基于网格离散化的数值计算。2019 年,Raissi 等[7]提出利用物理信息神经网络(physics-informed neural network, PINN)来描述对底层物理定律进行数学编码的新方法。为了通过深度学习获得PDE 的近似解,PINN关键步骤是将PDE的残差直接加入到神经网络损失函数中来指导网络的训练[8]。PINN作为一种新兴的内嵌物理知识的深度学习方法,在流体力学和传热领域得到了广泛实践[9-10]。以参数化的二维稳态导热为例,Gao 等[11]开发的物理信息几何自适应的卷积神经网络PhyGeoNet 已成功用于预测不规则表面的温度分布。与单纯的热传导相比,流动传热涵盖了速度场和温度场,是典型的多物理场系统。陆至彬等[12]将软边界PINN 和硬边界PINN 分别应用于两个二维稳态传热问题——具有内热源的热传导和平板间对流传热,结果表明由硬边界PINN构建的参数化代理模型预测能力更优。Laubscher等[13]在稳态和瞬态不可压缩层流下,利用PINN 分别模拟了成直线排列的双加热圆管的流动传热,与商业CFD 模拟结果的对比证明了PINN 求解多物理场的能力。与此同时,Laubscher[14]将其进一步推广到物性参数可变的多组分流动和传热模拟问题,以矩形区域内的干空气加湿问题为例,该工作的创新点在于使用三个独立的神经网络(PINN-3)来分别模拟对应的速度场、温度场和浓度场。与传统的使用单个神经网络的PINN求解多物理场作比较,研究结果表明PINN-3不仅能达到更小的训练残差,而且其预测组分浓度分布的性能要远优于传统的PINN。
以上对PINN 在传热应用方面的研究工作基本都是在流体或固体内部的传热,有待开发基于真实物性条件下共轭传热PDE 的求解策略和算法。但是,由于共轭传热内在的耦合性,若利用PINN 直接求解,将出现难以收敛的情况[15]。为了解决上述问题,NVIDIA 公司的SimNet 团队[15-16]借鉴共轭传热耦合的经典处理方法做了初步尝试。本工作则在此基础上进一步完善计算流程和算法,将分区耦合策略与PINN 结合用于模拟真实场景下的共轭传热现象,并深入分析算法的收敛特性及模拟结果。
1 共轭传热理论
1.1 基本理论
共轭传热是描述固体和周围流体之间热交互关系的传热现象,整个换热过程是固体导热和流体传热的组合[17-18]。假设流体流动状态为层流,对于稳态不可压缩流体,流体流动通常由连续性方程和N-S方程控制,如式(1)、式(2)所示。
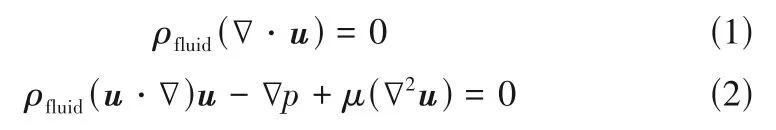
式中,u为流体速度,在三维空间x、y、z方向上的分量分别为u、v、w,即u=[u,v,w];ρfluid为流体的密度;p为压力;μ为流体的黏度。而流体传热则建立在流动的基础上,无内热源存在时,其控制方程描述如式(3)。
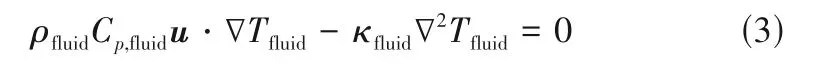
式中,Tfluid、Cp,fluid和κfluid分别为流体的温度、比定压热容和热导率。
在固体内部,仅存在热传导过程。对于无内热源存在的稳态热传导,可通过求解拉普拉斯方程来获得固体内部的温度场。

式中,Tsolid为固体温度;κsolid、ρsolid和Cp,solid分别代表固体的热导率、密度和比定压热容。
共轭传热涉及固体和流体的热交换。在流体和固体的界面处,温度和热通量传递的连续性[19]通过以下边界条件约束来控制。

式中,下角标sw和fw分别表示流固公共界面处的流体域壁面和固体域壁面。而热通量可通过温度梯度直接计算得出。
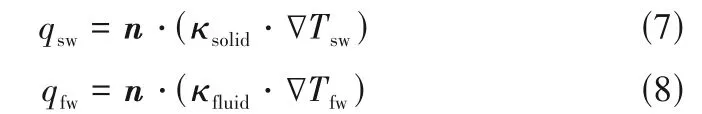
式中,n为壁面上向外的单位法向量;∇Tsw和∇Tfw分别为固体域壁面和流体域壁面的温度梯度。
1.2 分区耦合策略
分区耦合策略对流体域和固体域分别采用专门的求解器求解,并在两个域的界面上交换边界条件,通过迭代满足界面的耦合条件[20]。这种方法的优点是可利用现有的最先进的求解器分别独立求解流体域和固体域,但由于需要在两个域之间不断迭代,计算过程相对烦琐,耗时较长。
根据交换的边界条件(boundary condition, BC)的不同,分区耦合策略有不同的呈现形式。热边界条件可以分为以下三类:

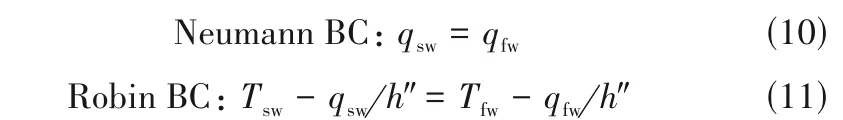
式中,h"为虚拟传热系数,并非物理意义上真实的局部传热系数,其在算法中的作用是辅助共轭传热问题收敛,可取任意数值,但取值时需兼顾计算时间和边界条件传递的稳定性[17]。
分区耦合策略的命名规则由Divo 等[21]提出,它规定流体域向固体域传递的方向为正向,固体域向流体域传递的方向则为反向。对于将流固界面处流体的热通量和温度作为固体域的Robin 边界条件、固体的温度作为流体域的Dirichlet 边界条件的情况,对应的耦合方法被称为传热系数正向温度反向 法(heat transfer coefficient forward temperature backward, hFTB)。

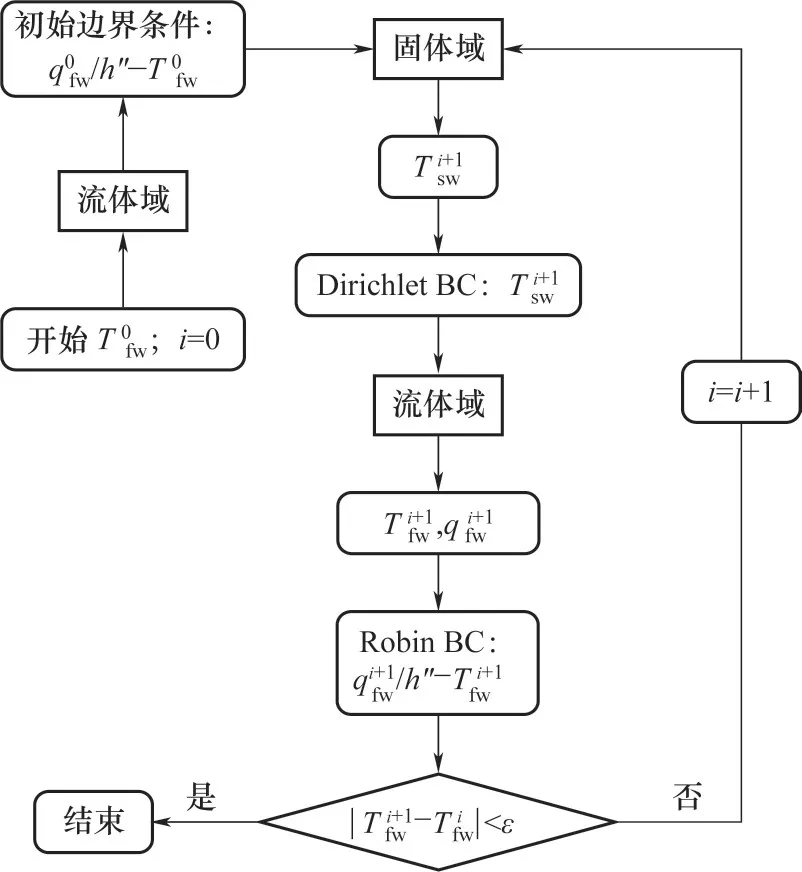
图1 hFTB方法的流程图Fig.1 Flow chart of the hFTB method

2 物理信息神经网络框架结构
上述共轭传热数值模型涉及的PDE 可用式(14)的通用形式表示。

式中,Г为非线性偏微分算子;f(x,λ)为原函数即PDE 的解;x和λ分别为域Ω上的空间坐标向量和参数向量(包括几何参数和操作参数)。若计算域为三维空间Ω⊂ℝ3,则x=[x,y,z];若为二维空间,则x=[x,y]。
求解上述PDE 需要指定边界条件,其通用表达如式(15)。

式中,B为涵盖Dirichlet、Neumann和Robin等边界条件的约束算子[6];∂Ω代表域Ω的边界;xb为边界∂Ω上的坐标点。
PINN 是建立在传统深度神经网络基础上的新型结构化神经网络,其基础框架见图2。根据框架结构和神经元连接方式的不同,神经网络可以分为全连接神经网络(FC-NN)、卷积神经网络、循环神经网络等[22]。由于FC-NN 能解决大多数的PDE 问题[23-26],本工作将利用其构建PINN。在FC-NN 结构中,每一层神经元的输出都作为下一层神经元的输入,这一前向传播过程的数学表达[12]为

图2中PDE的具体求解过程如下[6]。首先,构造一个输入为x和λ的神经网络f̂(x,λ;θ),拟将其作为PDE 的解析解f(x,λ)的代理模型,并可生成与f(x,λ)维数相同的输出向量。
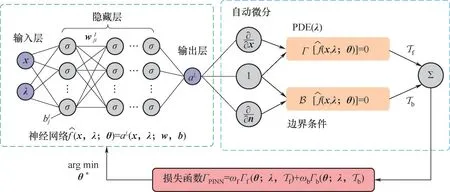
图2 PINN的经典框架示意图Fig.2 Schematic of a typical PINN framework

式中,θ={w,b}表示神经网络的权重矩阵和偏置向量;上角标L代表神经网络的输出层。
接下来,需要为神经网络提供样本量为|T|的训练数据集T={x1,x2,…,x|T|},它通常由两个相互独立的集合Tf⊂Ω和Tb⊂∂Ω组成,分别代表域内和边界上的样本集。为度量神经网络和约束之间的差异,PINN的损失函数ΛPINN(θ;λ,T)定义为PDE残差及边界残差的L2范数平方的加权求和,如式(19)所示。

式中,ωf和ωb为权重;xf为计算域内的坐标点;|Tf|和|Tb|分别为在域内和边界上采集的样本坐标点的个数。如式(19)所述,PINN 损失函数由两部分组成:Λf(θ;λ,Tf)用于约束描述物理定律的PDE,可称为“基于物理知识的损失”,Λb(θ;λ,Tb)则对应边界条件的损失。
最后,利用基于梯度的优化器(如SGD、Adam和L-BFGS)最小化损失函数来训练神经网络的权重和偏置θ= {w,b}。在训练过程中,PINN 还借助自动微分技术,可以方便地计算f̂(x,λ;θ)相对于输入x的梯度信息。当PINN 收敛到可接受的精度水平时,f̂(x,λ;θ*)可认为是数值模型f(x,λ)的代理模型。
3 案例研究
3.1 二维模型和三维模型
本工作以散热器系统作为研究对象,是基于一定假设的共轭传热模型[15,28]:带底座的三翅片散热器放置在横截面为矩形的通道内,组成的三维模型如图3 所示,图中下角标c 和b 分别代表通道和底座。散热器底座中央与芯片直接接触,芯片产生的热量传导给散热器。不可压缩流体从通道入口进入,流经散热器表面与其进行热交换。在三维建模中,以通道中心为原点(O)建立笛卡儿坐标系,三维模型关于xy坐标轴平面对称,二维模型的几何结构则选取其中的xy切面。
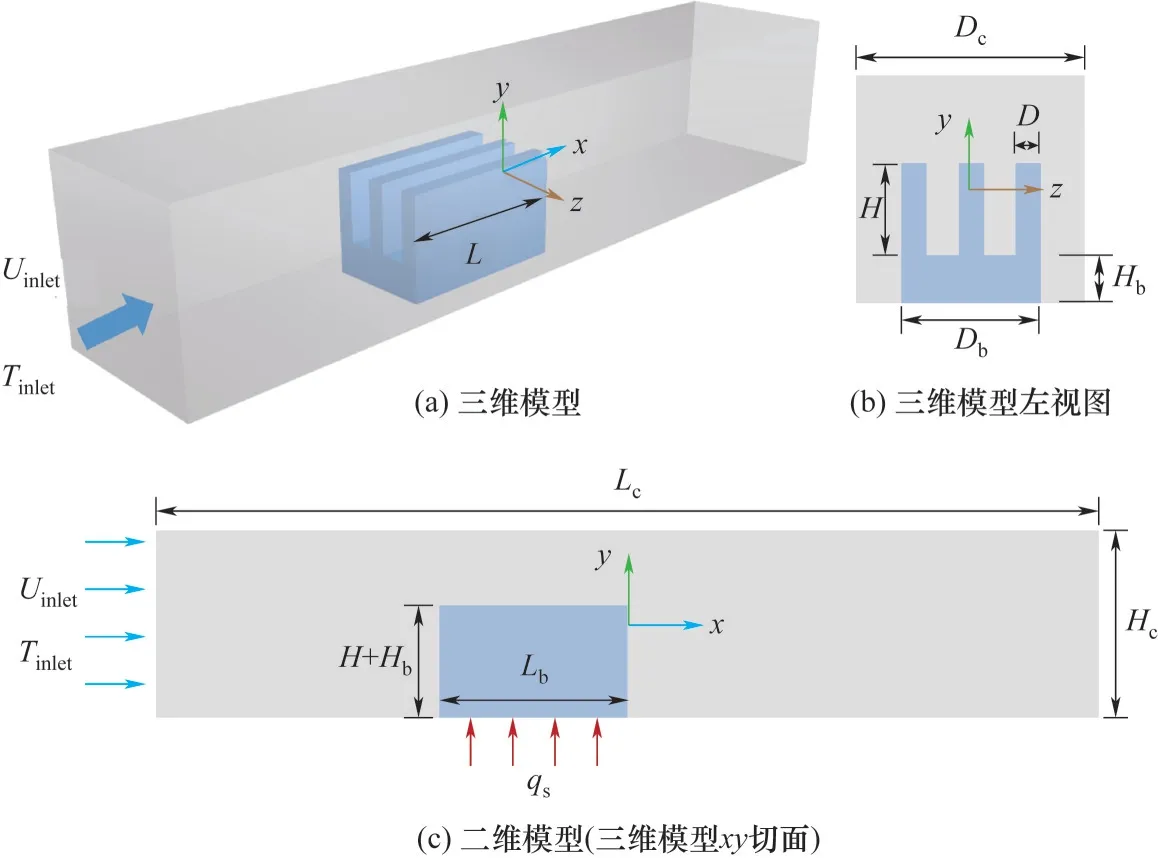
图3 共轭传热模型Fig.3 The conjugate heat transfer model
结合共轭传热基本理论,其数值模型由一系列PDE 共同控制,还需给定恰当的边界条件才能利用PINN进行求解。对于流动,假设流动状态为稳态层流,通道入口处流体速度已知(u=Uinlet,v= 0,w=0);通道出口处压力p= 0,通道和固体的壁面无滑移即u= 0。对于传热,假设通道入口处流体温度保持恒定,Tinlet= 293.15 K,通道壁面及出口处均被视为绝热,即[n· (κfluid·∇Tfluid) = 0]。最后,假设芯片在散热器底部产生均匀的热通量,指定输入系统的恒定热通量qs作为热边界条件。热边界条件的设置方式为

共轭传热模型的几何尺寸汇总在表1中。选取空气和铜分别作为流体和固体材料,假定物性不受温度影响且保持恒定不变,相应的物性数据在表2中列出[29]。需要指出的是,对于二维模型,相应的几何尺寸为三维模型尺寸的10倍,且固体底部整个区域施加均匀热源(即Ls=Lb),通道入口处的流体速度和输入热通量分别设为Uinlet= 0.1 m/s 和qs= 200 W/m2。而对于三维模型,通道入口处的流体速度和输入热通量分别指定为Uinlet= 1.0 m/s 和qs= 12000 W/m2。
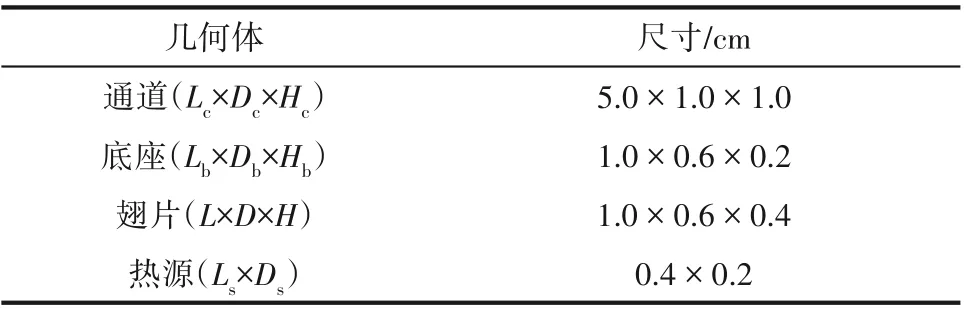
表1 共轭传热三维模型的几何尺寸Table 1 Geometric dimension of the 3-D conjugate heat transfer model
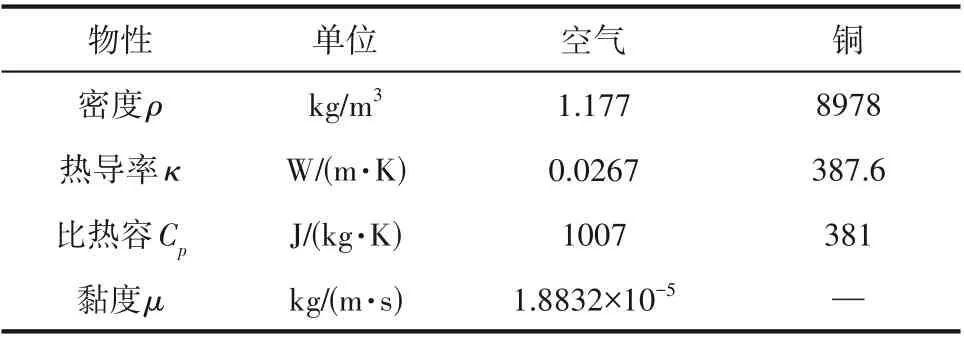
表2 流体和固体的物性Table 2 Fluid and solid properties used in the simulation
3.2 求解策略
综合上述分析,除了公共界面的热交互,传热过程在流体域和固体域都是相对独立的。鉴于hFTB 方法可利用求解器分别独立求解子域的特性[15],本工作提出分区耦合PINN 策略,其框架示意图如图4(a)所示。其中,由于在本工作中流体为不可压缩流体,流动和传热是单向耦合(one-way coupling),因此流体流动和传热可以分别单独训练。当流体流动网络flow_net 达到收敛标准后,其结果u*将作为训练流体传热网络heat_net_fluid 温度场的初始值。
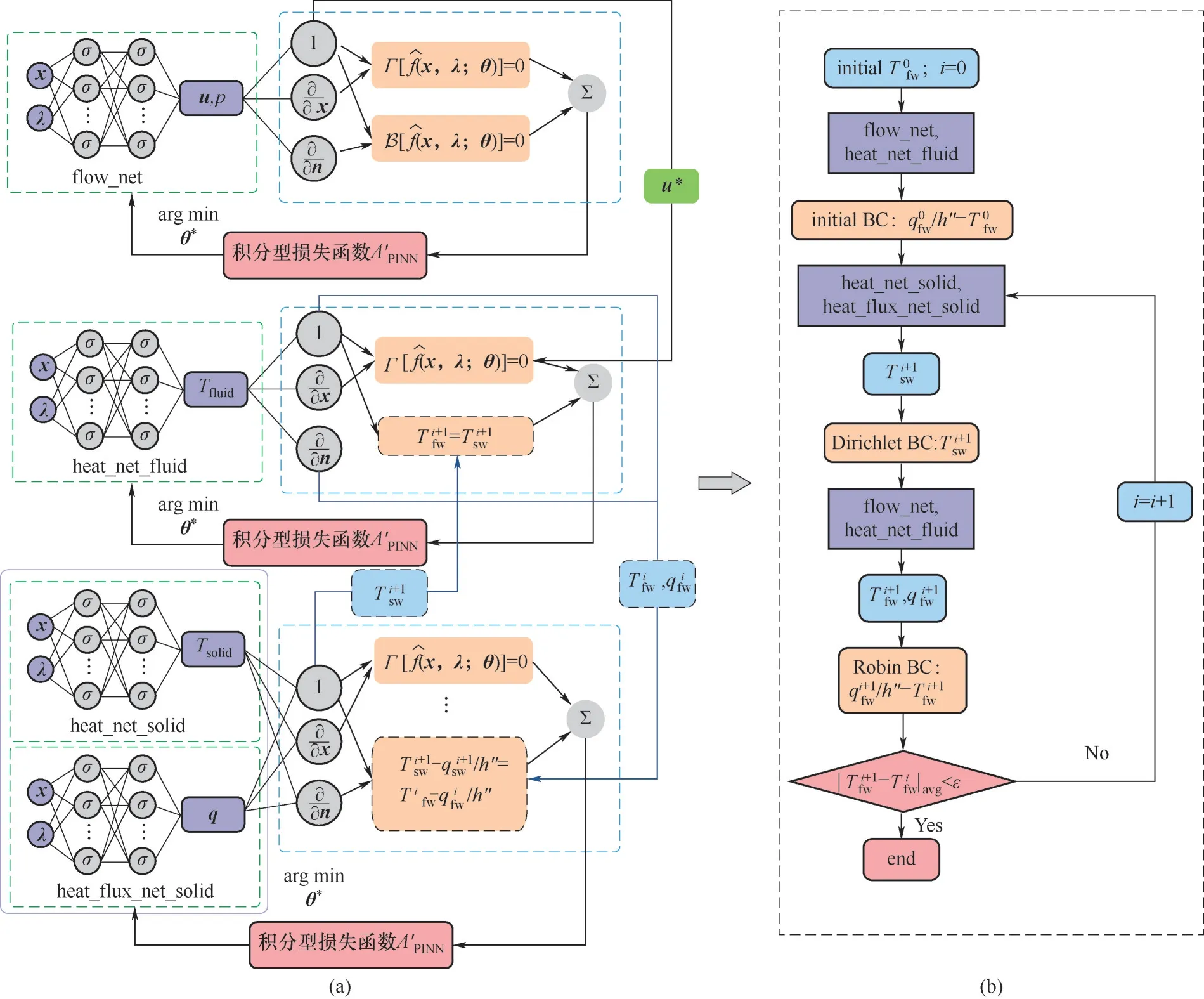
图4 PINN与hFTB方法集成的方法框架示意图和优化程序Fig.4 The partitioned coupling PINN strategy methodological framework and optimization procedure
在固体导热中,固体导热方程可展开为以下形式。

式中,q为与∇Tsolid维度相同的向量,在x,y,z方向上q= [qx,qy,qz]。与此同时,qx、qy、qz也满足二阶混合偏导数相等的定理约束,表达如式(24)。
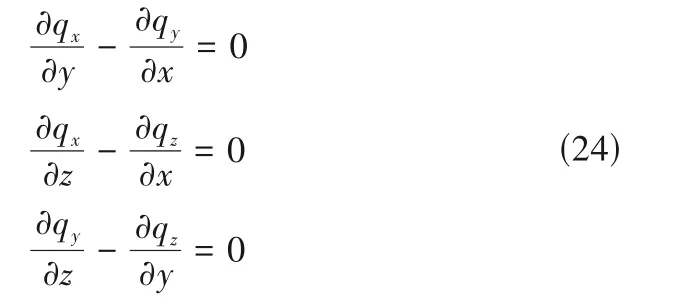
基于上述推导,本案例构造两个神经网络heat_net_solid、heat_flux_net_solid 来满足固体传热控制方程[式(22)~式(24)]的约束,其中heat_net_solid的输出为Tsolid,而heat_flux_net_solid 的输出为[qx,qy,qz],如图4(a)所示。值得注意的是,并不需要强制满足q和∇Tsolid之间等式约束,因此式(22)的处理方式打破了式(21)中固体温度梯度和二阶导数的强耦合关系。
为进一步提高PINN 求解物理模型的收敛性能,本工作采取Monte Carlo 积分(Monte Carlo integration)形式的损失函数来代替求和形式的损失[15],这一方法的好处在于确保域内单位空间内的损失一致,提高训练精度。
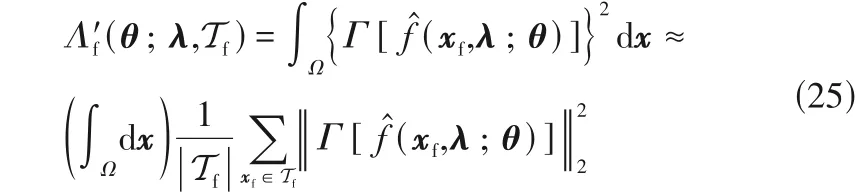
损失函数[式(19)]中权重ω的选择对于收敛至关重要。通常ω为不随空间位置变化的定值。然而,空间不同的位置梯度的变化程度不同,统一的权重显然不够合理。本工作通过引入几何体的符号距离函数(signed distance function, SDF)[30]改变不同空间位置的权重,其权重定义[31]如式(26)、式(27)。

式中,d(x)代表空间任意点x到域边界的最小欧几里得距离。根据函数定义可知,靠近域边界ω(x)会降低,而边界往往是梯度急剧变化的地方,因此SDF 加权有利于降低急剧梯度对收敛的影响,加快收敛速度的同时还可能提高精度。引入Monte Carlo积分和空间加权ω(x)后最终的PINN 损失函数形式如式(28)。

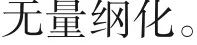

式中,上角标*表示经过无量纲化后的参数和变量;Lscale、tscale、Mscale和Tscale分别表示长度、时间、质量、温度四个与流体力学相关的基本物理量放缩的比例。类似地,所有物理量都是根据其对应的基本量纲的幂次表达进行处理。在本案例中选取的放缩比例在表3 中列出,其目的在于使得无量纲参数和变量范围在0~1内更有效地训练神经网络[15]。

表3 无量纲放缩比例参数Table 3 Non-dimensional scaling parameters
本研究中设置PINN 隐藏层为6 层,每层256 个神经元,激活函数为swish 函数,流体流动网络最大训练步数设置为1×106步以保证收敛。此外,流体传热和固体传热网络每次循环的最大训练步数均为3×105步,二维模型和三维模型的虚拟传热系数h"分别设为500 和600。PINN 训练过程基于NVIDIA Modulus 工具包所提供的深度学习集成平台[31],工作站配置为2块GeForce RTX 3070 GPU。
4 结果与讨论
二维模型的允许温度最大误差取ε=0.10 K,采集每次循环结束后流固界面处的温度用于监测收敛过程,收敛历史如图5 所示,其中|Ti+1-Ti|即为|T i+1fw-T ifw|avg,在经过20 次循环后,已满足循环终止条件,且在循环过程中流固界面处空气和铜的温度差异逐渐变小,在循环终止时已趋于相等,再次证明温度场已收敛。

图5 二维模型流固界面处温度收敛历史Fig.5 Temperature convergence records at the fluid-solid interface of the 2-D model
训练后的结果与COMSOL 模拟结果进行对比以验证PINN 模型的精度。为进一步定量比较PINN预测值与CFD 模拟值的差异,采用归一化平均绝对百分比误差(normalized mean absolute percentage error, NMAPE)作为量化指标[14],其计算公式如式(30)所示。
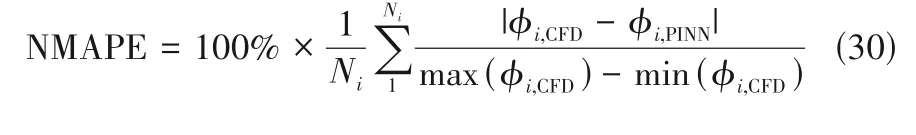
式中,ϕ代表物理量;下角标CFD 代表COMSOL的模拟结果,其中温度最小值统一取入口温度。
二维模型速度场、压力场和温度场的PINN 预测结果如图6 所示。从整体上看,多物理场的预测结果与COMSOL 模拟结果趋势一致,这证明了分区耦合PINN 求解真实场景下二维共轭传热的有效性。进一步对比NMAPE 可知,NMAPE 值均小于4%,其中固体温度的NMAPE 数值最小。尽管二维模型固体温度云图的对比观察到较为明显的差异,但需要注意到固体温度分布的变化范围很小(不超过0.06 K),且温度的绝对误差最大为0.19 K,因此PINN 仍相对准确地捕捉到了固体温度的分布。此外,速度场云图较大的差异主要集中在通道出口附近,除了速度分量v,速度分量u和压力场的预测误差都超过2%,最终造成流体温度更大的预测误差(约4%)。
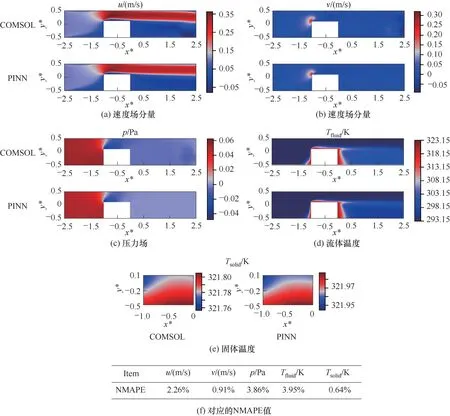
图6 二维模型结果对比Fig.6 Comparison of the results of the 2-D model
对于三维模型,考虑到计算精度可能会有所下降,故允许温度最大误差设置为ε=0.20 K,其收敛历史如图7 所示,在经过17 次循环后,已满足收敛准则。尽管循环开始时流固界面处空气和铜的温度差异很大,但在经过4次循环后两者便快速接近,之后则缓慢趋于相等。

图7 三维模型流固界面处温度收敛历史Fig.7 Temperature convergence records at the fluid-solid interface of the 3-D model
三维模型速度场、压力场和温度场的切面结果对比如图8 所示,为便于比较,流体域取y* = 0 处平行于xz平面的切面,固体域取经过散热器中心且平行于yz平面的切面。由图可知三维模型PINN 预测的速度场出现更长更明显的尾迹,但与二维模型相比NMAPE 的变化不大,这可能得益于压力分布预测精度的改善(三维模型压力的误差明显下降)。不同于二维模型,三维模型速度场预测精度的提高进一步降低了流体温度的预测误差,但是固体温度的误差则较为显著。与此同时,固体温度云图直观地表明了这一差异,其最大绝对误差为2.12 K,这可能是三维结构更为复杂所导致的,但NMAPE 计算结果仍小于4%。总地来说,分区耦合PINN 求解真实场景下三维共轭传热已实现较好的精度,但还需深入的研究来进一步降低固体温度的误差。

图8 三维模型结果对比Fig.8 Comparison of the results of the 3-D model
5 结 论
通过将分区耦合策略与PINN 相结合,本工作提出利用传热系数正向温度反向法来构建共轭传热问题的分区耦合PINN 模型。同时,本工作基于真实物性体系,提出分区耦合PINN 模型的通用收敛准则和算法,克服了PINN 直接求解共轭传热的收敛难题。以共轭传热二维模型和三维模型分别探究了分区耦合PINN 的预测精度,模拟得出二维模型和三维模型的固体温度最大绝对误差分别为0.19 K和2.12 K,NMAPE值均小于4%。结果表明分区耦合PINN 是解决真实场景下共轭传热问题的有效方法,为共轭传热参数化代理模型的构建提供了理论指导。

