基于分子热力学性质和密度峰聚类的脱硫汽油集总

李怀旭，孙晓岩，陶少辉，夏力，项曙光

（青岛科技大学化工学院，过程系统工程研究所，山东 青岛 266042）

引 言

随着石油加工领域进入分子管理时代，业内逐渐形成一套完整的油品分析模拟体系，即油品分子表征（重构）-组分集总（划分）-解集总（还原）体系。油品分子表征通过现代化分析仪器进行[1-3]，在此基础上依靠计算机辅助方式构建分子体系的模型化方法来进行分子重构[4-7]。油品真实分子组成在带来更丰富信息的同时，也极大增加了炼油过程模拟和优化模型的规模，导致计算量激增，因而如何在尽量保留油品真实分子组成信息的同时，有效减少组分数以提高炼油过程的模拟与优化效率，是石油分子管理体系亟待解决的关键问题之一。而集总过程则可以根据一定规则将油品分子划分为少数几个虚拟组分，是减小过程模拟计算规模的有效方式[8-9]。如在油藏模拟领域，Montel 等[10]首次提出通过迭代的动态聚类（dynamical clustering,DynC）算法将大量组分通过性质的相似性进行集总，将150 个组分用少于10 种虚拟组分替代，并提出了虚拟组分物性的计算方法。基于少量虚拟组分进行模拟后，为获得模拟结果中的产品真实组成，Leibovici 等[11]通过闪蒸计算实现解集总（delumping）来还原油品组分，封松等[12-13]在其构建的分子级组成模型中利用可逆集总方案的映射规则倒推产品分子组成。

Montel 等[10]对真实组分进行集总时，采用了需要事先指定类别数和初始聚类中心的迭代动态聚类算法，但针对特定体系，确定虚拟组分数目需要进行大量的分析和比较，且聚类结果对于初始中心的选择极为敏感[14-16]。这些弊端使得动态聚类在实际应用时难以产生稳定的结果，即使Montel 等提出通过人工选取类别数量最多的组分为中心可以使算法变得更稳定，但这是基于经验的，依赖于使用者对数据集的了解程度。对于过程模拟计算而言，往往希望得到一套稳健高效的集总计算模型，以适用于不同类型的数据。

基于此，本工作对油品分子的虚拟组分划分数目（即集总数目）对模拟计算的影响进行讨论分析，将机器学习领域中一种无须事先指定类别数和聚类中心的密度峰聚类（density peak clustering,DPC）[17]算法引入油品分子的集总过程，以真实分子的热力学性质为聚类变量，从而实现对表征汽油分子的集总，同时以相平衡与精馏计算对方法的有效性进行验证。

1 模型与方法

1.1 DPC算法原理

DPC 算法基于一个核心假设，即认为给定数据集的中心一定是该数据集中密度较大且互相远离（相对距离较大）的一些数据点。因而该算法的计算过程取决于数据集的距离矩阵dn×n（n为样本个数）和每个点的密度ρi。距离是聚类算法中常用的相似性度量标准，采用何种距离计算公式取决于不同种类的算法和目标数据集的分布情况。这里采用Montel等[10]提出的距离公式来度量数据点i与j间的差异，如式（1）所示。

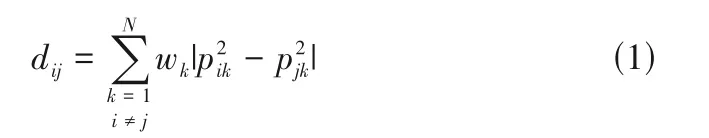
式中，wk为不同性质（维度）的权重值；pik与pjk为数据点的性质值；N为选取性质的个数（即数据集的维数）。采用式（1）度量性质之间的相似性旨在扩大性质间的微小差距。对于数据点的密度，本文采用高斯核计算数据点的局部密度[18-19]：

式中，dc为截断距离，其物理意义是用于判定数据点的疏密程度，定义为将距离矩阵的元素升序排列，其1%～5%处对应的距离。需要指出，dc为该算法唯一需要人工指定的参数，Rodriguez 等[17]的研究结果表明，其在一定范围内调节有助于更好地发现中心点。

相对距离δi定义为数据点i与所有密度大于点i的数据点之间的最小距离，对于密度最高的数据点，相对距离表达式为

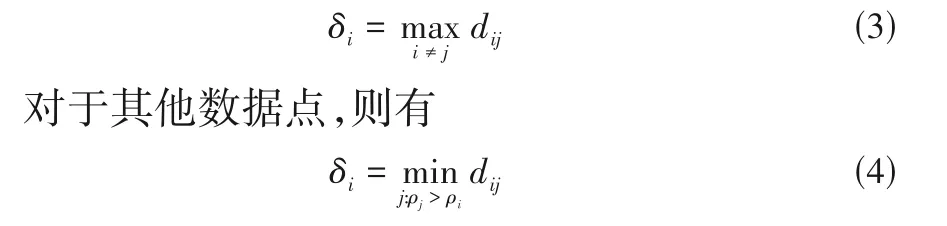
根据各数据点的ρ和δ可做出二维平面决策图，在图中明显离群的数据点即为类中心点，后文实例应用时将会详细展示如何寻找中心点。得到中心点后，将其余点分配给比其密度高的最近邻点所在的类别即可。DPC算法步骤如下所示。

（1） 对数据集进行标准化处理，将所有性质变量变换到[0,1]区间；

（2） 通过式（1）计算距离矩阵dn×n：

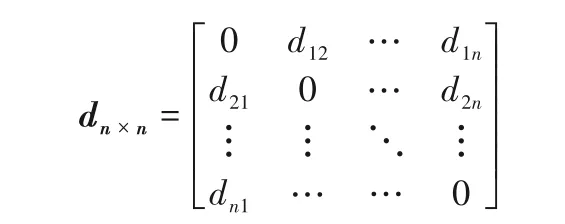
（3） 通过式（2）计算每个数据点的密度；

（4） 通过式（3）、式（4）计算所有数据点的δ；

（5） 做出决策图并选取类中心；

（6） 按照分配机制分配其他数据点。

由上述步骤可知，DPC 算法应用到油品分子的集总划分时的优点为：（1）无须预定中心点，这使得在确定虚拟组分数目时有足够的参考；（2）算法所得到的类中心是隶属于数据集的真实样本，且将每一类看作是数据空间中被低密度区域分割开的稠密区域，故能检测到任意形状的数据集，对于非球形数据集有很好的适用性，一些研究已经对此加以证明[20-25]；（3）DPC 算法流程中无迭代过程，类中心的发现和其余点的分配都是一次性完成的。这意味着在预先计算好距离矩阵后，DPC 算法效率不受数据集维度影响，而动态聚类法虽然在处理大量数据时有良好的伸缩性，但需要反复地迭代计算距离并重置中心点，且迭代结果受初始中心的影响很大，每次的聚类结果也都存在差异[26-28]。

1.2 集总性质选择

Montel 等[10]提出以Peng-Robinson（PR）状态方程参数a、b、m以及分子量四个参数作为集总性质，其中参数a、b、m分别通过式(5)～式(7)求得。

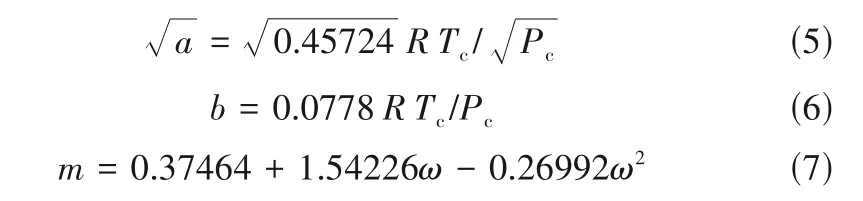
可见，参数a和b均由临界压力Pc和临界温度Tc求出，m由偏心因子ω求解，四个参数除了能很好地反映纯物质的临界特征和极性特征外，还能体现各个组分在热力学过程中的性质变化，且与进行模拟计算时选取的热力学计算方法保持一致。此外，Montel 等[10]建议a、b、m以及分子量（MW）在计算相似度时的权重值分别为1.0、1.0、0.1、0.5，这里也采用此权重值。

1.3 虚拟组分物性估算

对于集总得到的虚拟组分的物性计算，Leibovici 等[29]提出了集总系统特性估计方程对集总组分信息损失进行最小化处理，该方法准确且与使用的热力学模型完全一致。但在集总组分过多的情况下，该方法计算过程过于复杂，且本文侧重于研究集总划分方法而非热力学计算，故在虚拟组分物性计算方面，本文采用一组简单的石油馏分物性估算模型集合来进行计算，具体如下所述。

临界温度和临界压力采用Riazi-Daubert 模型计算，模型关联式如式（8）、式（9）所示[30]。

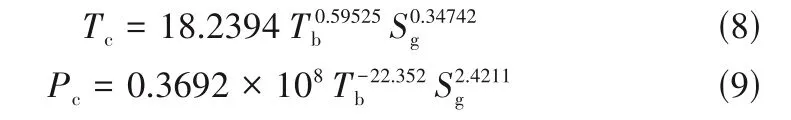
式中，Tb为正常沸点；Sg为相对密度。

偏心因子采用Lee-Kesler 模型计算，关联式如式（10）所示[31]。

式中，xi表示第i个组分；c为组分总数。相对密度（Sg）可以用分子量和沸点通过关联式估算，故这里不再收集每个组分的密度，其他诸如液相摩尔体积、水溶性、黏度、汽化潜热等性质的计算模型见文献[32]。

2 实例应用与讨论

2.1 数据来源

油品数据来源于某催化汽油吸附脱硫工艺体系的287 种真实组分，其中包括C2～C12烯烃、C3～C12正构烷烃、C4～C10异构烷烃、C5～C10环烷烃、C6～C12芳烃以及二十余种含硫烃类化合物。

为方便比较，以a、b、m和MW 四个参数为数据特征。图1 显示了287 个数据点的分布情况，每一个子图显示了两个性质间的相互关系。从对角线的直方图和其余散点图可以大致判断出由油品分子性质组成的数据集有三个主要特征：(1)a、b、m和MW 归一化数值都大量集中在0.25～0.75 之间；（2）组分两两性质之间的线性相关性较差（拟合优度在0.79～0.95 间）；(3) 数据集在二维平面上呈现出不规则的条状或椭圆状形态，大部分数据点处于高度密集且重叠的状态，不同类别之间没有明显的界限。显然这对于一般的聚类方法而言很不友好。

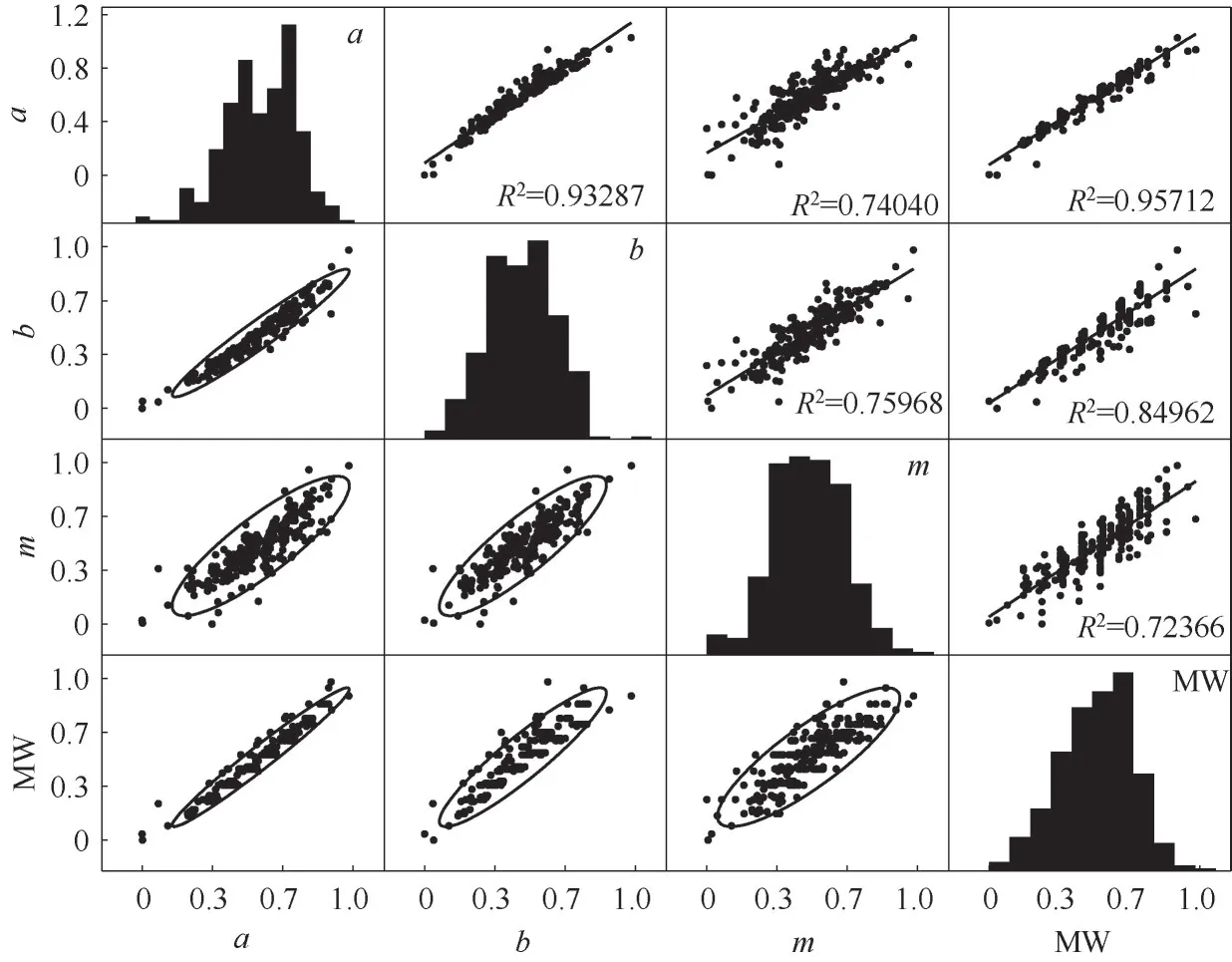
图1 标准化后的数据分布Fig.1 Standardized data distribution

2.2 集总数目对计算结果的影响

对于动态聚类而言，集总数目的选择会影响最终的集总效果，因此下文将通过指定压力（0.1 MPa）和汽化分率以计算物流温度的闪蒸过程，讨论不同集总数目对计算结果的影响。

图2 展示了使用动态聚类的集总方法将287 种真实组分分别集总为4、6、8、16、21种虚拟组分的闪蒸计算结果。显然，计算结果的准确性与集总数目密切相关。当集总数目为4 个时（4 components, 4 Comp），虚拟组分的闪蒸曲线的斜率小于真实组分，因为过少的集总数目会使得每个虚拟组分中包含许多性质差异较大的组分，从而使其热力学状态变化难以描述实际情况，同样6 Comp 时亦如此。再者，计算误差也会因系统中虚拟组分数量太少而扩大。随着集总数目的增加，真实组分得到更细致的分配，其闪蒸温度曲线的斜率更接近实际情况，但当集总数目太多时（21 Comp），许多本该属于同一类别的组分被强行分配到不同类别，特别是对于密集分布的数据集，这会导致集总类别之间出现链式效应，即相邻的每个虚拟组分的性质都会产生较大的误差。

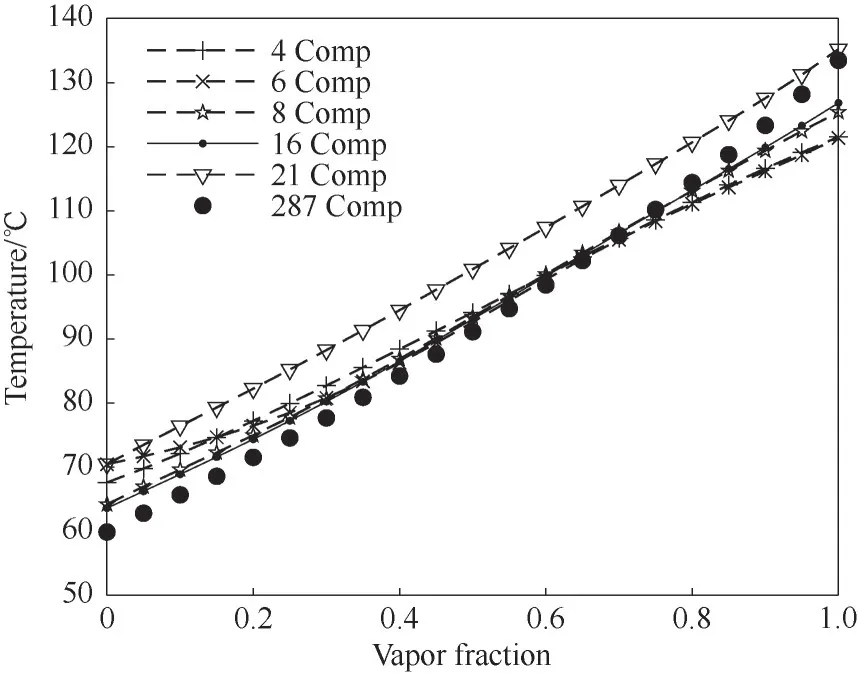
图2 不同集总数目在0.1 MPa下的闪蒸计算结果Fig.2 Flash calculation results at 0.1 MPa for different lumping

考虑多个集总数目下，不同汽化分率时的闪蒸温度的平均绝对误差（mean absolute deviation,MAE），得到如图3 所示的变化趋势（对0 个集总数目下的MAE做了缩小处理）。这说明集总结果的准确程度并不是随着集总数目的增加持续上升，这中间存在或大或小的波动。理论上，集总数目越多，计算规模便越大，复杂度自然也越大。本例中，集总数目在10～16 之间时，MAE 较小，集总数目持续上升至21时，MAE出现激增，而后又出现骤降。

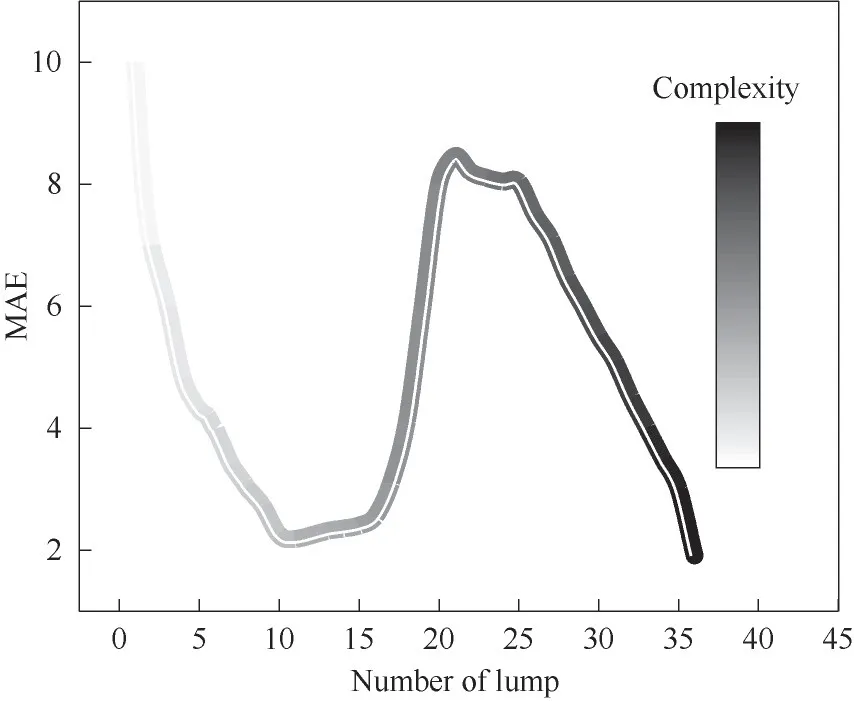
图3 闪蒸温度的平均绝对误差和计算复杂度随集总数目增加的变化Fig.3 Variation of MAE and computational complexity of the flash temperature with the increase of the number of lumps

一般地，以误差的大小衡量集总结果的准确性，得到图4（a）所示的变化趋势。Opt（optimal）代表最优集总数目，此时较少的虚拟组分数量却有较高的准确性；Lim（limit）代表极限集总数目，此时的集总数目等于组分个数，相当于每一个组分作为一个集总。小于Opt的部分代表许多性质差异大的组合更多地被集总在一起。Opt 到Lim 之间代表最优集总数目下的虚拟组分被拆开，其子组分先是被互相划分到与其性质差异较大的类别中，后又得到了更精细的组合，此时的复杂度也更大。图4（b）描述了一种简化情况来表示Opt-Lim 间虚拟组分的划分情况，P1,P2,P3 为Opt 中的某三个虚拟组分，实线圈起的部分代表原本正确的划分被拆开，虚线圈起的部分代表被拆开的子组分重新组合为新的虚拟组分（假设新的虚拟组分比之前划分的更加精细）。

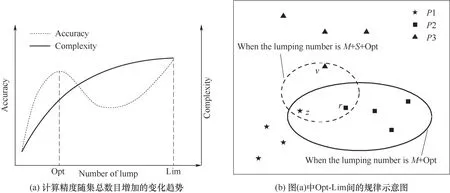
图4 计算精度与组分分配情况随集总数目变化的示意图Fig.4 Schematic diagram of the variation of calculation accuracy and component distribution with the number of lumps M, S—增加的集总数目; v, r, z—真实子组分

此发现具有一定意义，说明在组分集总过程中，确实存在一种兼顾效率和准确性的可能，而DPC 集总方法的作用就在于自适应地发现图中所示的Opt。需要指出，当物性估算模型依赖于摩尔分数权重时，这一规律并不明显。因为对于含量很少的组分，即使被错误分配，对虚拟组分的性质影响也不是很大。但对于含量高的组分（尤其是重组分），差距将会很明显。

2.3 DPC集总过程

首先根据式（1）、式（2）计算得到距离矩阵d287×287和局部密度ρi，其中dc取1%计算（经试验，本例dc在1%～5%内变化对最终聚类结果影响很小），再根据式（3）、式（4）得到δi，得到如图5（a）所示的平面决策图。图中彩色的数据点为明显离群的点，根据算法假设，这些数据点的共同特征是同时具有较大的δi和ρi，这意味着它们彼此相互远离且拥有各自的稠密区域，故将此视为数据集的10 个中心点。为了更清晰地展示类中心点与其他数据点区别，将每个数据点的ρ2和δ相乘，记作γ并降序排列，采用Lv 等[33]提出的一种通用阈值计算方法计算γ阈值（详细算法过程参见该文献），如图5（b）所示，从决策图中获取的10 个中心点在图5（b）中依然得到了突出显示。就此将油品中含有的287个烃类分子划分为10类，即10个虚拟组分。

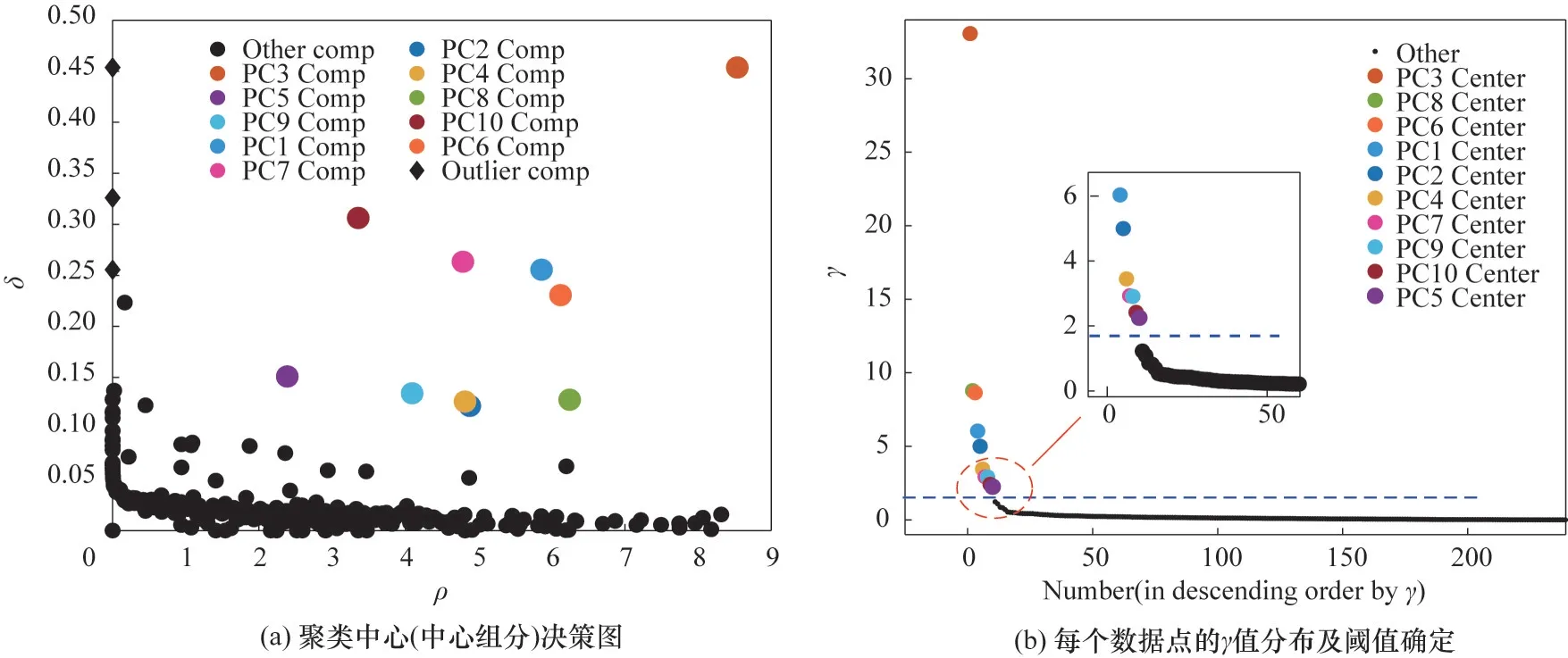
图5 集总数目及中心组分的决策图Fig.5 Decision diagram of the number of lumps and center components

此外，决策图中的黑色菱形标记也是数据集中明显离群的数据点，但与彩色的中心点不同，菱形点只有较大的δ，其ρ却异常小（接近于0），这说明此类数据点彼此孤立且相互远离，在整个数据集中不属于任何一类，本文将其定义为“离群组分”。对于其他ρ极小的点（紧靠纵坐标轴），因为其δ并不突出，故不能作为离群组分，这类点通常处于“团簇”的边缘。通过查找，3 个离群组分分别对应正十二烷、碳二苯并噻吩、1,4-二异丙苯（按δ值降序），其部分性质已经列于表1，与其他组分比较发现，它们具有个别较为突出的性质，因此将其视作“离群”是合理的。对于离群组分，本文的处理方式与算法要求不同（Rodriguez 等[17]认为每个离群点应单独为一类），本文建议两种处理方法：若离群组分数量太多，则将其归为一类，作为一个虚拟组分；若其数量较少、含量低，则将其包含在较近的类别中。本例中仅含2个离群组分，且为重组分，故采取第二种处理方法。

表1 离群组分的部分性质Table 1 Partial properties of outlier components

需要指出，本例中含有硫化氢气体和二氧化硫气体，其理论上也为离群组分，但算法并未侦测到两者，在此有必要做出解释：DPC 集总过程使用了式（1）来度量组分间的相似性，式（1）虽能扩大性质间的差异，但有一个潜在问题，即对于较小的数值并不灵敏。如图6 所示，点Ⅰ、Ⅲ代表两个离群组分，点Ⅱ代表某正常组分，且假设A、B、C为三个组分的性质。其中点Ⅰ的性质比点Ⅱ低50%（反向差距），点Ⅲ的性质比点Ⅱ高50%（正向差距），若采用欧氏距离计算空间中的真实距离，则两者与点Ⅱ的相似度是一致的，两者都应该计算出较小的ρ，进而得到较大的δ，最后形成孤立点。但当采用式（1）时，反向差距大的组分得不到较大的相对距离，即使它看起来与正向差距大的组分并无区别，这便导致了所有类似的组分不能在决策图中突出显示。本例中，H2S 和SO2具有很小的分子量，很低的临界温度和很大的临界压力，故其a、b、m、MW 均很小，算法没有对其进行挖掘。实际上，诸如SO2等不凝气或一些杂质气体往往单独从油品分子中划分出来，所以在检测离群组分时可以不考虑这一类反向差距很大的组分；相反，重组分的侦测更加重要，同时也更难侦测，而式（1）对于正向差距大的组分敏感性更强，故这种处理方法是合理的。

图7（a）为最终集总结果，图中的不同着色代表不同的类别，即反映不同真实组分所属的虚拟组分，对角线的直方图汇总了每种虚拟组分的性质分布情况。通过观察图1 发现，参数a、MW 相关性较其他更高，为更直观地显示集总结果，暂时忽略性质a，仅对b、m、MW 进行三维可视化，如图7（b）所示。经集总得到的虚拟组分的部分物性由式（8）～式（14）计算，与其中心组分的性质一并列于表2。

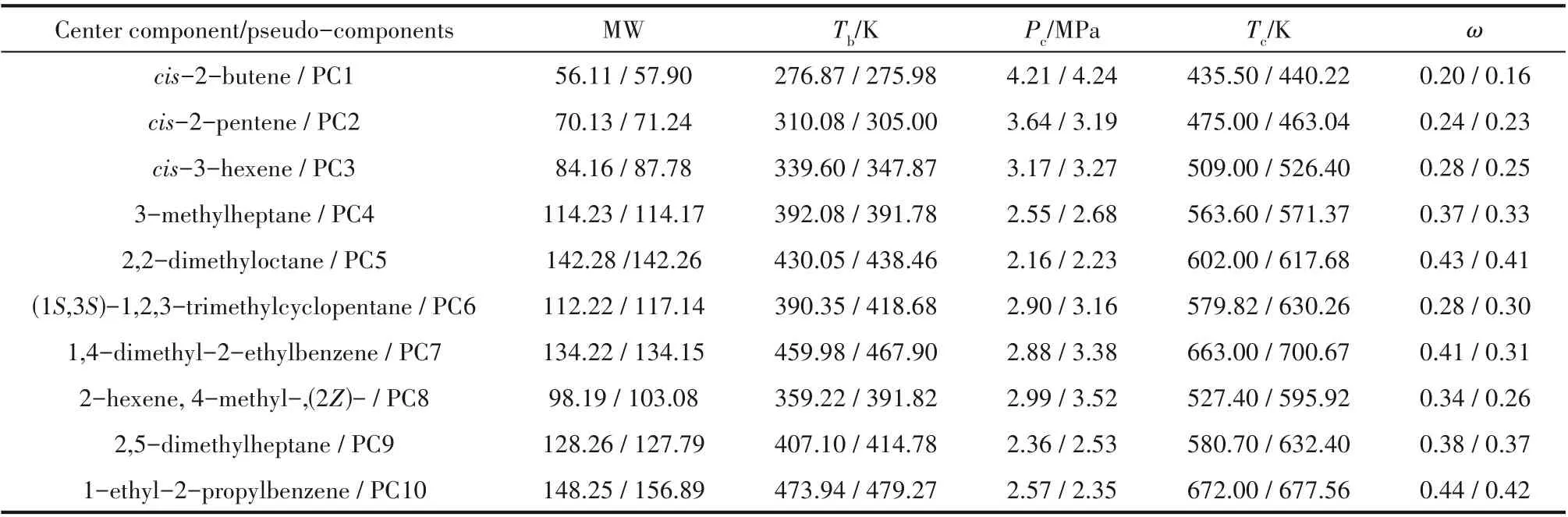
表2 中心组分与对应的虚拟组分的部分性质Table 2 Partial properties of center components and corresponding pseudo-components

图8展示了每个虚拟组分中子组分的分子类型和碳原子数。可见，PC4 和PC5 分别主要包含C8异构烷、C10异构烷，两者数量较少，即所谓的“小簇”。关注数据集中的“小簇”极为重要，这在一定程度上能反映算法对数据进行挖掘的彻底性。从图7（b）中又可以发现两个“小簇”都分布在PC6和PC10中，而PC6 包含较多C8～C9的异构烷及环烷，PC10 则主要为C11以上的芳烃。

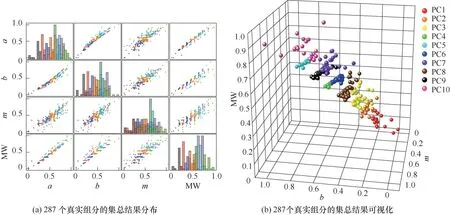
图7 287个组分的集总结果分布及结果可视化Fig.7 Lumped results of 287 components and visualization of results

表面上，不管从数据集分布形态还是具体组分来看，似乎PC4 应隶属于PC6。但实际发现，PC4 中10 个组分的平均偏心因子为0.38，而PC6 中39 个组分的平均偏心因子仅为0.30，且有近半数的组分的偏心因子小于0.30，这说明PC6 中组分的极性与PC4 有明显差距，将此团数据集分成两类是符合实际的。对于PC5 而言，结合图8（a）和图8（b）可以很直观地发现其与PC10 中的组分性质差距更大，PC10 以C11以上的芳烃为主，其极性较大，而PC5 以C10以下的异构烷烃为主，其极性要小于芳烃。再者，通过比较发现，PC5 中组分的平均临界压力为2.17 MPa，平均临界温度为337℃，而PC10 为2.52 MPa、415℃，两者存在明显差距。而DPC 集总方法恰好可以有效地对PC4 和PC5 进行挖掘，这得益于该算法擅长处理具有重叠性的非球形数据集。

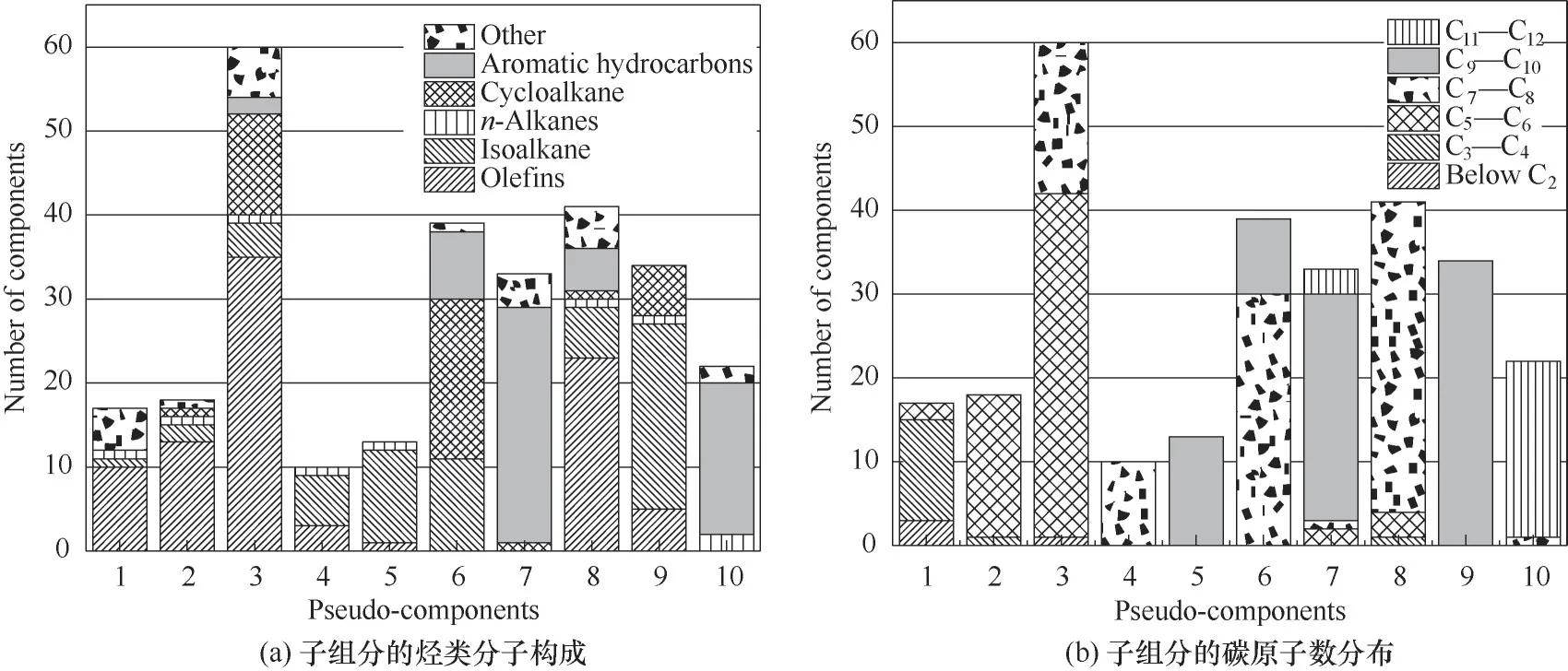
图8 虚拟组分中子组分的烃类分子构成和碳原子数分布Fig.8 Hydrocarbon composition and carbon number distribution of the subcomponents of pseudo-component

2.4 相平衡计算验证

本文重在考察虚拟组分在汽液相平衡计算中的表现。Leibovici 等[11]在其体系已证实了基于动态聚类的集总方法在闪蒸计算中的可靠性。需要指出，基于动态聚类的油品集总方案需要预先指定集总数目，为便于比较，将基于DPC 算法集总得到的10 个虚拟组分作为其预先设定的集总数目。下面展示了DPC 集总方法和动态聚类方法与真实组分的对比。

很明显，DPC 方法取得了预期效果。图9 中，其闪蒸温度曲线与真实组分的贴合程度较高；而采用动态聚类的集总方法即使预先给定了一个近乎合理的集总数目，其效果与DPC 方法相比也有一些差距，尤其是在接近露点温度时误差较大，原因是动态聚类无法捕捉不规则或具有层叠性的数据，故部分数据点被划分到了与自身性质差异较大的类别中，进而在宏观上引起了计算结果的差异。从图9得出，DPC 集总方法所得到的闪蒸温度的MAE 较动态聚类方法而言下降36.0%，计算精度有明显提升。

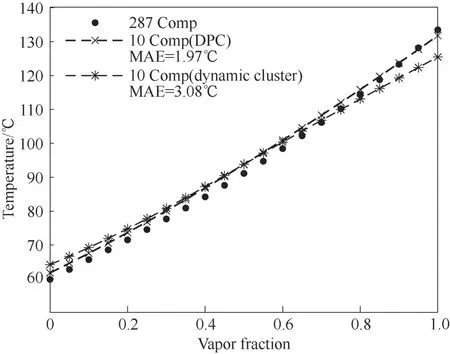
图9 不同集总方法在0.1 MPa下的闪蒸温度曲线对比Fig.9 Comparison of flash temperature curves at 0.1 MPa for different lumped methods

图10为不同集总方法在0.1 MPa下的闪蒸热负荷的绝对误差随汽化分率的变化。与真实情况相比，DPC 方法得到的各点误差均在较小范围之内，而基于动态聚类的方法只有在汽化分率0.7～0.8 之间才能达到与其持平的效果。从图10得出，DPC 集总方法所得到的闪蒸热负荷的MAE 较动态聚类方法而言下降64.2%，计算精度有明显提升。热负荷是对虚拟组分的热容、焓值等性质的综合考察，故此结果在一定程度上说明了DPC 集总方法的可靠性。

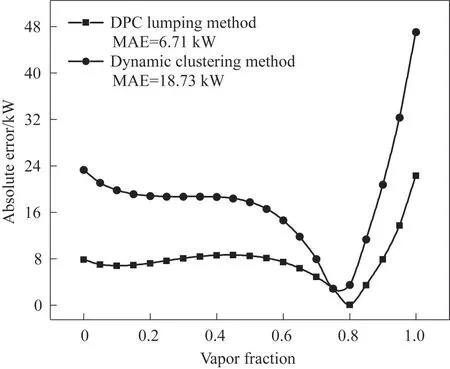
图10 不同集总方法下闪蒸热负荷的绝对误差（与真实组分下的热负荷相比）比较Fig.10 Comparison of the absolute error of the flash heat duty(compared to the heat load of the real component) of different lumped methods

2.5 中心组分和虚拟组分的比较

前文已述，通过DPC 算法得到聚类中心隶属于真实组分，其在一定程度上能代表子组分的性质，故有必要讨论中心组分是否可以表征油品分子的真实性质。图11、图12展示了中心组分和虚拟组分分别表征油品时的结果对比。由图可见，在汽化分率小于0.1 时，中心组分代替真实组分的效果尚好，但随着汽化分率的增大，其闪蒸温度总是低于真实情况，这说明中心组分中有过多的轻组分（相比于虚拟组分而言较轻）。从图12 的PT 包络图来看，临界条件的低估又说明中心组分的极性和沸点难以反映真实情况。表3中列出了每个虚拟组分与中心组分的沸点差距，可见PC6 的中心组分的沸点比虚拟组分低28.33 K，PC8 的中心组分的沸点比虚拟组分低32.60 K。

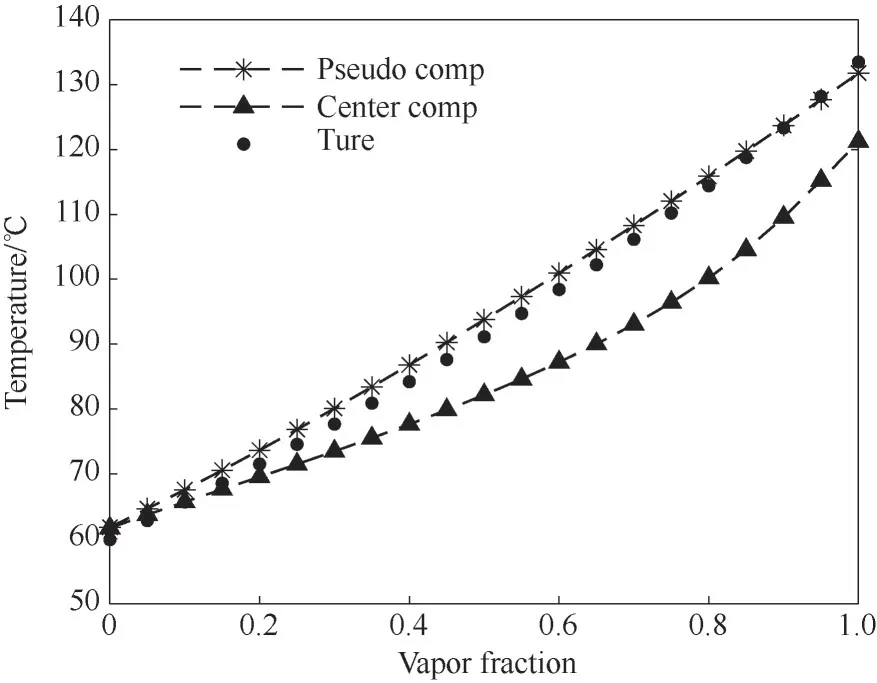
图11 中心组分与虚拟组分在不同汽化分率下的闪蒸温度对比（0.1 MPa）Fig.11 Comparison of the flash temperature of the center component and the pseudo-component at different vaporization fractions at 0.1 MPa

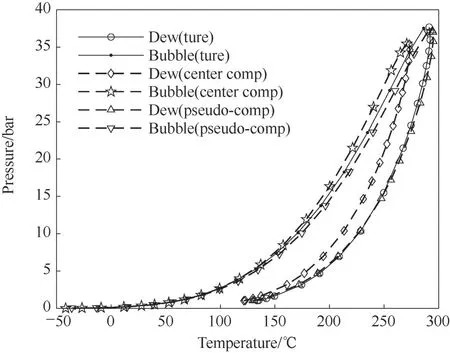
图12 中心组分与虚拟组分的PT相包络图对比（1 bar=0.1 MPa）Fig.12 Comparison of the PT phase envelopes of center component and pseudo-component

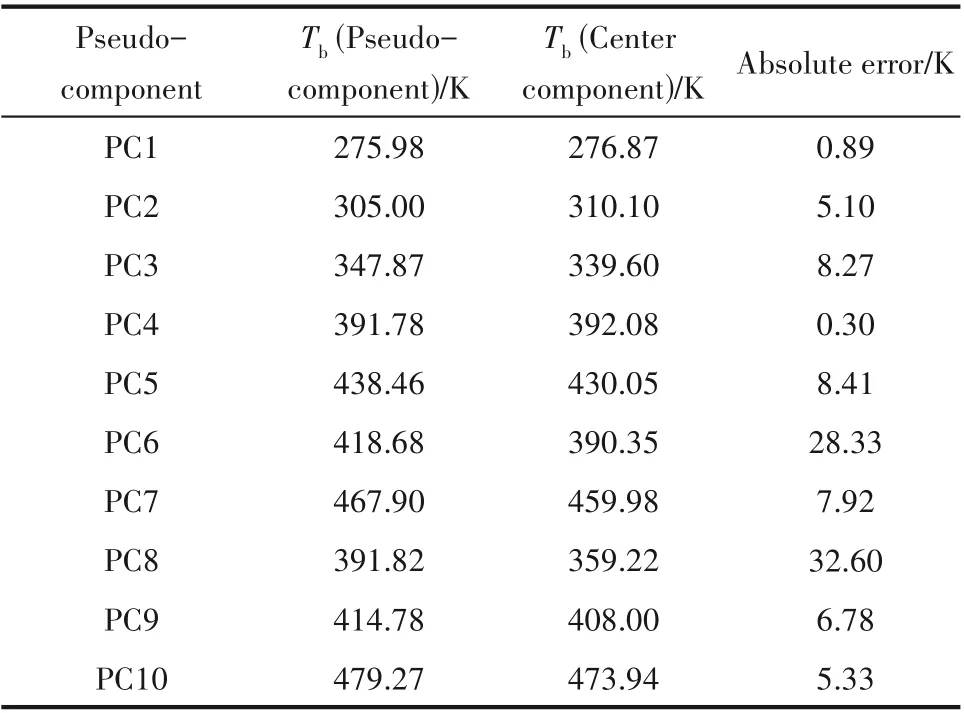
表3 各虚拟组分与其中心组分的沸点差距Table 3 Boiling point gap between each pseudocomponent and its center component

虽然中心组分目前不能完全反映虚拟组分的性质，但分析其中的原因尚有价值。实际上，通过算法得到的虚拟组分，可看作是空间中一块稠密程度从中心向周围不规则发散的区域。如图13（a）所示，以b和m为特征性质，将PC8 中子组分的局部密度ρ映射到气泡图中，图中面积最大的点为中心组分，可见，ρ较大的组分全部靠近中心组分，这些组分的性质与中心组分更相似；而ρ较小的组分距离中心组分较远，其与中心组分的相似度也就较差（相比于本类别中的ρ较大的组分而言）。更直观地，图13（b）的密度分布热力图展示了中心组分对其子组分的描述能力大小。热力图的核心部分（黑色区域）为中心组分，它对其周围的密度接近自己的点能很好反映；但对稍微远离的点（绿色及蓝色区域），其代表性是有限的。对于包含子组分较多的虚拟组分，由于当前数据分布的不规则性，其中心组分很难描述到每一个组分的性质。而用虚拟组分来表征真实油品时，实际上等同于用图中低密度的点去修正中心点，只是修正过程涉及了其区域中的全部点。

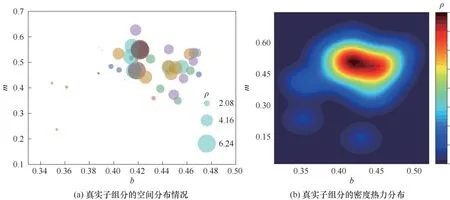
图13 PC8中每个真实组分的局部密度与所在空间位置的可视化Fig.13 Display of local density and spatial location of each real component in PC8

2.6 精馏模拟验证

下面使用ASPEN 进一步验证集总方法的性能。使用本文方法（DPC）和动态聚类法（DynC）分别得到的10个虚拟组分进行常压精馏模拟，并与真实组分的结果进行对比。此外，还将动态聚类法得到的两种不恰当集总的结果也加入比较。进料条件及塔参数设置如图14所示，模拟结果的对比展示于图15 中。显然，使用虚拟组分替代真实油品进行精馏模拟时，方法面临了严峻挑战：随着D/F（塔顶采出量与进料量之比）的增大，4 个集总结果的塔顶采出温度均被高估。其中DynC（10 Comp）方法的塔顶温度MAE 为5.03℃，塔釜温度MAE 为4.34℃，相比之下DPC 方法取得了更可令人接受的结果，其塔顶温度的MAE 为1.95℃，精度提高61.2%；塔釜温度的MAE 为2.01℃，精度提高53.7%，这为下一步的“组分还原”奠定了相对可靠的基础。

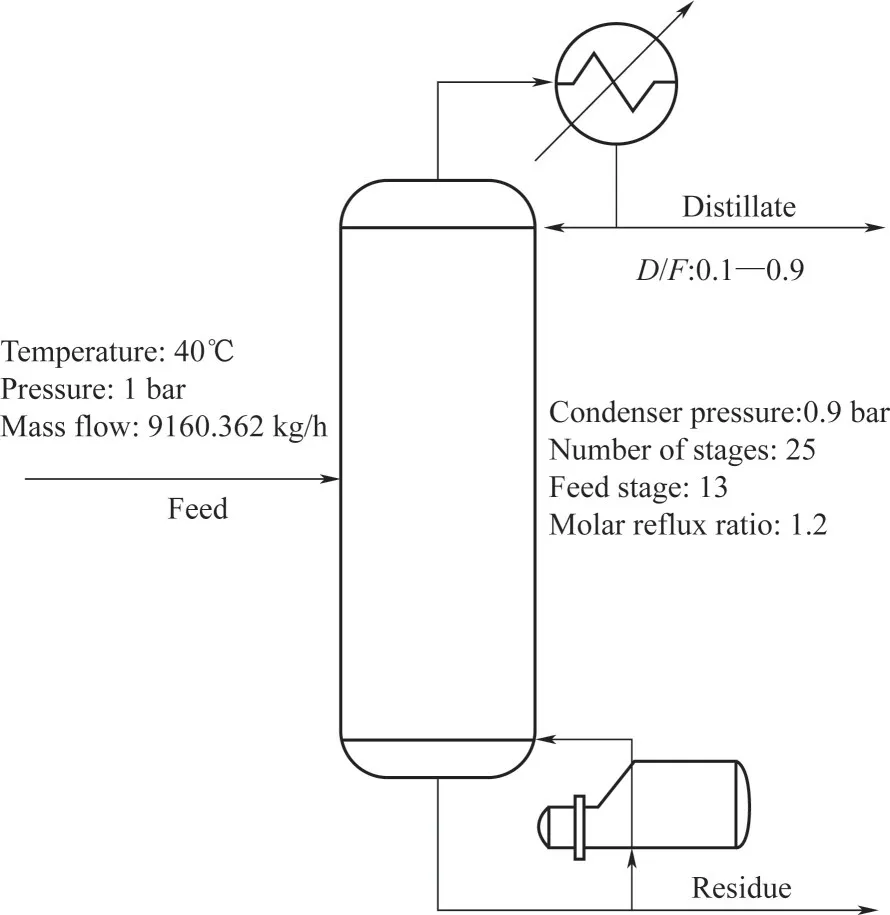
图14 进料条件及精馏塔参数设置Fig.14 Feeding conditions and distillation column parameter settings

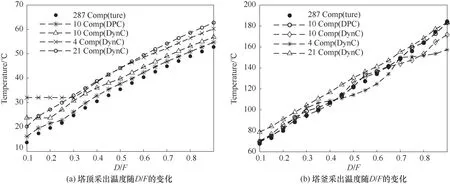
图15 不同集总结果下的精馏计算结果Fig.15 Calculation results of distillation of different lumped results

2.7 模拟计算效率

当组分数目增加时，精馏塔的待求方程组规模也随之增大，故采用少数虚拟组分代替大量真实组分进行模拟计算和调和设计时，在计算效率上无疑是有明显进步的。下面以ASPEN 为模拟计算工具，使用微型计算机对10 个虚拟组分和287 个真实组分的精馏计算时间(CPU 使用时间)进行比较（针对第2.6节中的流程），计算机的硬件配置如下。

通过MATLAB 与ASPEN 的通信功能获取到两种情况的计算时间(含程序的打开/关闭时间，每次计算前均保证CPU 占用一致)如下：287 个真实组分为47.856 s，10 个虚拟组分为9.671 s。显然两者存在显著差距。此外，若过程模拟涉及包含精馏塔的撕裂流收敛，或针对精馏塔进行优化，则计算效率的差距将更大。

3 结 论

将基于密度峰的聚类算法思想引入油品分子集总过程，实现了集总数目（中心组分）的自动侦测和脱硫汽油组成的可靠划分，并以某装置的脱硫汽油实例进行验证，得到以下结论。

（1）在油品分子集总过程中，存在一个兼顾效率和准确性的集总数目，而本研究提出的方法借助决策图即可简便地确定这个集总数目和少数离群组分，这在一定程度上克服了估计集总数目时的主观性和盲目性。此外，该方法可对油品性质数据集中分布不规则的数据或“小簇”进行有效挖掘，在一定程度上避免了传统划分方法造成的分配错误，从而使油品分子得到更精确的划分。

（2）中心组分代替真实油品的能力是有限的；而虚拟组分可综合其子组分（真实组分）的性质，更好地反映真实情况。但中心组分作为真实组分，其热力学计算相比于虚拟组分而言是严格的，关于中心组分描述真实油品的能力是否可以优化，还有待进一步讨论。

（3）实例验证结果表明，DPC 集总方法得到的虚拟组分可以满足相平衡计算的要求，该方法对于将来构建完整的石油组分分子水平划分具有较大潜力。

本工作在集总性质的选取方面，现阶段使用了固定的热力学性质组合及性质权重，并未考虑是否有更优的选择。考虑到不同炼油工艺过程可能对所需的性质组合和权重值要求不同，故之后的工作重点在于，通过优化性质组合提高集总结果对油品的可描述性以及不同需求下的最优权重设计。

符 号 说 明

c——虚拟组分中的子组分总数

dc——截断距离

dij——数据点i与数据点j的相互距离

MAE——平均绝对误差

MW——分子量

N——集总性质个数

n——油品真实组分总数

Pb——正常沸点下的压力，MPa

Pbr——正常沸点下对比饱和蒸气压

Pc——纯组分临界压力，MPa

pik——数据点i的第k个维度（性质）的值

R——气体常数，8.314 J/(mol·K)

Sg——相对密度

Tb——沸点，K

Tbr——对比正常沸点

Tc——纯组分临界温度，K

wk——维度（性质）k的权重值

γi——ρi与δi的乘积

δi——第i个数据点的相对距离

ρi——第i个数据点的局部密度

ω——偏心因子

下角标

i,j——组分的样本序号

k——性质的样本序号