考虑饱和特性的电动汽车双向变换器控制策略

张振波， 王海云*， 王维庆

(1.新疆大学电气工程学院, 乌鲁木齐 830047; 2.教育部可再生能源发电与并网控制工程技术研究中心, 乌鲁木齐 830047)

随着中国“双碳”目标的提出，能源问题日益严峻，在不久的未来，以化石能源为动力的燃油车将逐渐被清洁、环保的电动汽车取代。数量庞大的电动汽车作为移动式储能电站，通过双向功率变换器实现电网与汽车间能量双向流动：在白天用电高峰期将汽车多余电量回馈到电网，起到肖峰的作用；在夜间用电低谷期，利用电网过剩的发电量给电池充电，起到填谷的作用[1-3]。双向功率变换器作为能量流动的桥梁，对电网、汽车蓄电池起到至关重要的作用。

目前，汽车双向功率变换器结构主要分为单级式和多级式两种[4-5]：单级式双向变换器只有一个双向交流变直流(AC-DC)环节，实现整流逆变功能，双级式双向变换器包含有双向交流变直流和双向直流变直流(DC-DC)环节，其中直流变直流环节可以对直流电进行升降压变换。因此，相比于单级式结构，双级式结构功率变换器可以适应更宽范围的蓄电池电压[6]，在实际应用中得到快速发展。中外学者对双向功率变换器控制策略进行了广泛研究，文献[7]针对电流过大造成解耦不充分提出采用平均电流控制解耦，电压外环带宽窄，响应速度慢有效减弱干扰；电流内环带宽较宽，响应速度快有利于电流跟踪，平均电流解耦控制，可以有效降低大电流冲击造成的不充分解耦。但由于电压外环带宽窄，会造成响应延迟，影响响应速度。文献[8]提出一种基于双序前馈解耦控制策略，通过双旋转坐标系分离正负分量，消除一个分量在坐标的影响，然后采用单一坐标分量控制解耦，提高解耦精度。文献[9]提出一种电压定向的PR控制策略，将采集的旋转坐标系下的交流电压通过坐标变换转换成直角坐标系，再经过比例谐振(proportional resonance，PR)控制器，对交流电压分量进行无静差跟踪，从而获得精准调制的空间矢量脉宽调制波(space vector pulse width modulation， SVPWM)对开关管进行控制，实现电网与电动汽车能量的双向流动。但该控制策略引入了新的控制器，造成反馈调节次数增加，影响了动态响应速度。文献[10]采用一种适用于电动汽车充放电的虚拟同步机控制策略，在电网电压暂升暂降和网侧输入功率变换的情况下，对电动汽车充放电模式进行分析，验证了该控制策略的可靠性。但该控制策略只能针对单一电压等级的电池进行充放电，局限性较大。文献[11]提出一种基于卡尔曼滤波的电流内环解耦控制，采用电流解耦控制加比例式脉冲补偿控制的方法，能有效地解耦电流分量，该控制策略鲁棒性能和稳定性较好，同时还具有更低的总谐波失真值。文献[12]为了实现快速充放电，提出一种双闭环前馈解耦，采用脉冲充电和恒流放电进行汽车与电网能量交换，但未考虑电感饱和会造成的解耦不充分，造成控制精度下降。

针对上述研究现状，现首先介绍双向功率变换器的基本电路拓扑结构，并在此基础上提出一种基于二阶广义积分器(second-order general integrator，SOGI)的电流控制的车载双向功率变换器控制策略，该策略采用二阶广义积分器实现正交信号构造，相比于传统的延时构造法，提高系统响应速率，同时采用连续积分无电感解耦方法，避免电感饱和造成前馈解耦不充分，从而有效提高脉冲宽度调制(pulse width modulation，PWM)控制精度。采用不同大小的电流对电池进行充放电，实现快充与慢充相互切换的目的，使电池达到深度充电，避免长时间使用大电流充电导致电池过热，有利于延长电池寿命。最后，通过仿真和试验验证该控制策略的可行性；使得在充电电流较大时，电感仍能处于非饱和状态，准确控制充电电流，避免对汽车电池造成破坏，提升汽车使用年限。

1 双向功率变换器工作原理

车载双向功率变换器作为连接电网与电动汽车能量传输的纽带，通常由滤波模块、前级双向AC-DC模块、后级DC-DC模块和电池模块组成[13]。

变换器工作在充电状态时，前级AC-DC变换器从电网吸收电能，将交流电整流为直流电，并保持直流端母线输出电压恒定；后级DC-DC变换器工作于Buck降压斩波模式，将充电电压、电流控制在电池要求内。变换器工作在放电状态时，后级DC-DC变换器工作于Boost升压斩波模式，将电池电压升高至中间直流母电压；前级AC-DC变换器将直流电逆变成交流电，再反馈给电网[14]。其主电路与控制电路结构如图1所示。

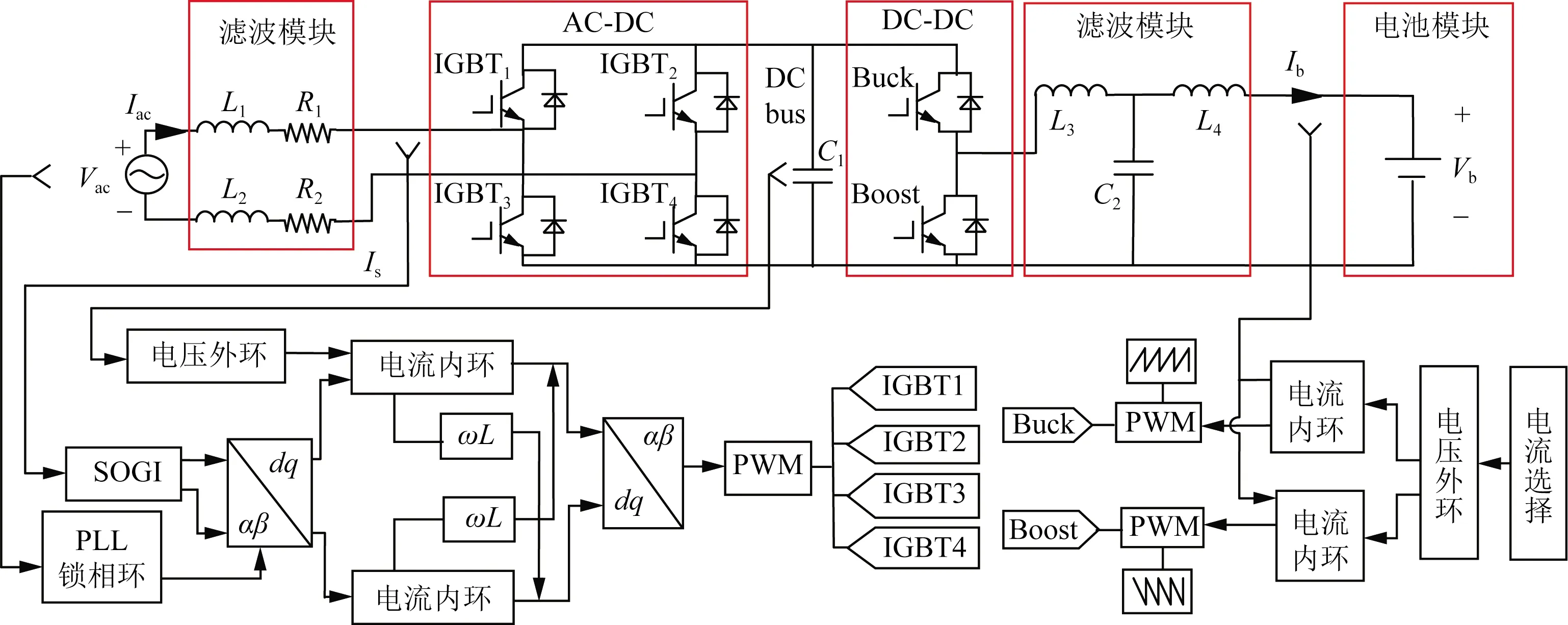
Iac为交流电源电流；Vac为交流电源电压；L为电感；R为电阻；C为电容；DCbus为直流母线；Buck为降压斩波信号；Boost为升压斩波信号；Ib为电池电流；Vb为电池电压；Is为交流侧电流；αβ、dq为帕克(Park)变换；ω为谐振频率；PWM为脉冲宽度调制信号；IGBT为开关管控 制信号图1 双向功率变换器拓扑图Fig.1 Topology of bidirectional power converte

2 双向变换器控制策略

2.1 SOGI控制

在前级AC-DC变换器的控制中，由于单相整流电路只存在一相电流，在进行闭环控制时，缺少一个自由度，所以无法进行同步坐标变换。传统电感解耦控制通过延时法获取彼此相位差为90°的一组电流信号，然后用于解耦控制，但该方法响应时间慢，在电网波动时极其不稳定，对系统稳定性产生影响。采用二阶广义积分器SOGI获取网侧电压电流相位，从而构造一组虚拟正交信号，进行坐标变换[15]，提高响应速度，增加系统稳定性。同时SOGI在产生一对正交信号时，还可以有效滤除电网谐波，提高响应速率。如图2所示。

k为阻尼系数；ω为谐振频率；Iα为电流Is在α轴的分量；Iβ为电 流Is在β轴的分量；s为变量符号，无实际意义图2 SOGI结构框图Fig.2 Structure block diagram of SOGI

由图2可知，SOGI的传递函数为

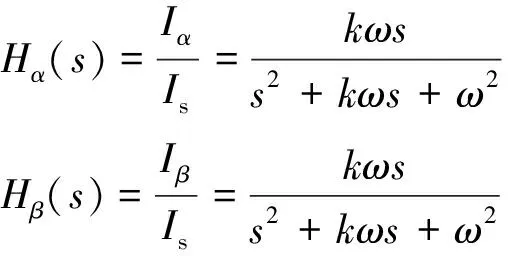
(1)

当谐振频率调至电网基波频率即(ω=ω0)，此时输出一对具有严格意义的正交信号，即

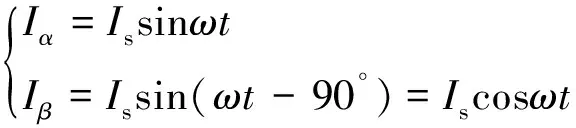
(2)

通过SOGI可以得到两个彼此相差90°的正弦信号Iα、Iβ，再通过Park变换得到d轴、q轴分量，其变换矩阵为

(3)

式(3)中：θ为锁相环相位角。将式(1)代入式(2)可得

(4)

将式(3)整理可得

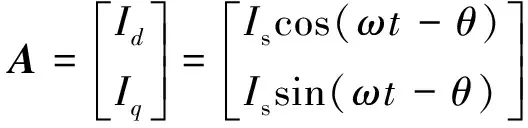
(5)

由式(5)可知，通过二阶广义积分器将单相电流分解为相位彼此相差90°的两相电流，用于后续解耦控制的反馈输入。

2.2 传统电感解耦控制

根据基尔霍夫电压定律(kirchhoff’s voltage law，KVL)方程得到单相AC-DC整流器在dq旋转坐标系下的数学模型：

(6)

式(6)中：ed、eq为电网电压在d轴、q轴的分量；ud、uq为交流侧电压在d轴、q轴的分量；Id、Iq为d轴、q轴的电流分量；R1为电路阻抗；t为时间。

由式(6)可知，单相整流器在dq坐标系下的数学模型与三相整流器相同，d轴分量与q轴分量相互耦合，将Id、Iq作为电流内环被控对象，进行比例积分(proportional integral，PI)控制，由于ed和eq中含有Id、Iq的耦合项，故需要对变量Id、Iq进行前馈解耦，传统的前馈解耦采用电感解耦模式，如图3所示。

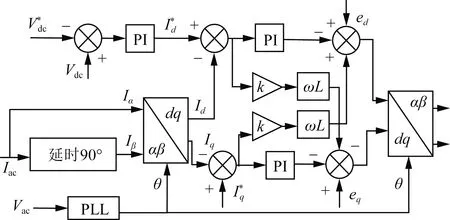
Vdc为直流母线参考电压；Vdc为直流母线实际电压；为d轴参考 电流分量；为q轴参考电流分量；PLL为锁相环图3 传统电感解耦控制框图Fig.3 Block diagram of traditional inductance decoupling control

前馈电感解耦控制为

(7)

式(7)中：Kip为比例控制系数；Kil为积分控制系数。

图3中，电网采集的交流电经过延时90°获得旋转坐标下的两项电流Iα、Iβ，再经过dq变换得到反馈值，用于电感解耦。但传统控制策略通过延时法构造两项电流，影响了控制速率，同时电感解耦控制在电流过大时会造成电感饱和，使系统不能完全解耦，从而造成控制精度下降。

2.3 改进型无电感解耦控制

改进型无电感控制通过在前馈解耦时采用连续积分模块，来避免电感L因电流过大导致饱和，造成解耦不充分。

由式(6)和式(7)联立得

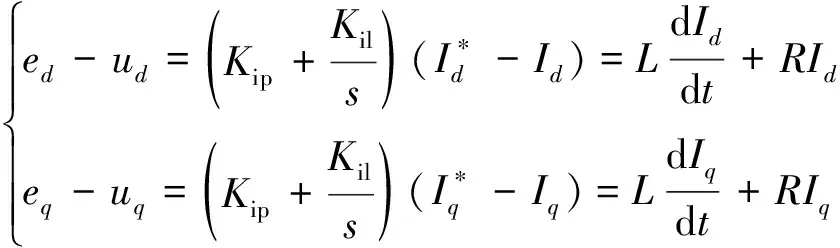
(8)

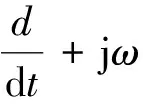
(9)

将jωLId作为一个整体，通过PI进行控制，设计PI控制为

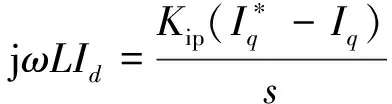
(10)

将式(9)和式(10)代入式(8)化简得

(11)

由式(11)可知，改进后的无电感解耦控制中ud、uq不含有电感L，通过PI控制系数与连续积分就可实现对电流的完全解耦，因此避免了电感饱和造成的不完全解耦，提高了控制精确性。其控制框图如图4所示。

后级DC-DC升降压斩波电路采用电流控制的PWM方式，是一种双闭环控制模式，相比较于电压控制的单闭环控制模式来说，电流控制具有动态响应快，稳态性能优越等特点。对输出电池侧电压进行采样，与设定参考电压Vref进行比较，将误差输入PI控制环路进行比例积分控制，输出结果加上电流参考值，作为电流基准值，将采集的电池侧电流与基

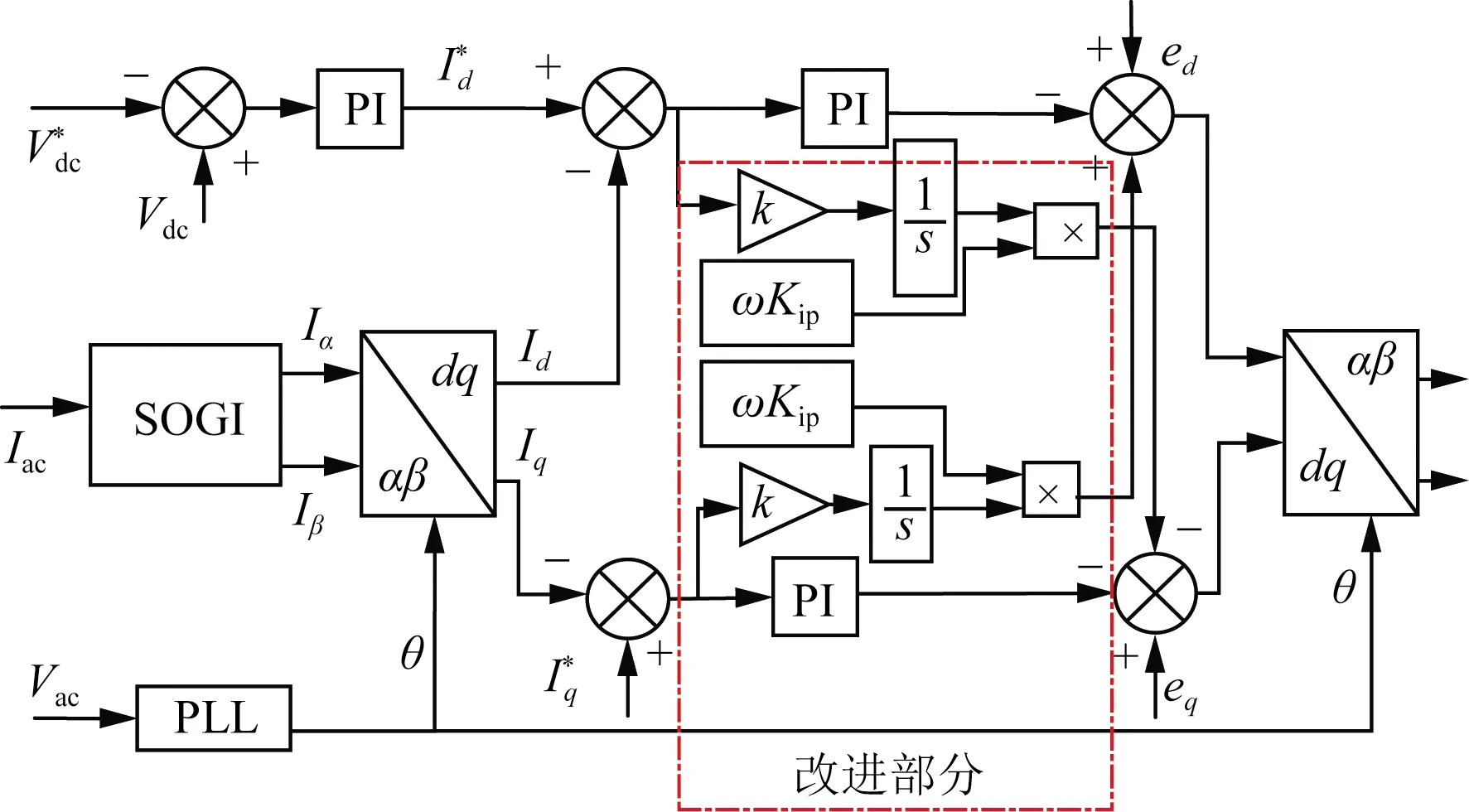
图4 改进型无电感解耦控制框图Fig.4 Improved non-inductive decoupling control block diagram

准值做误差，经PI控制器调节后，输出结果与锯齿波进行调制，生成驱动信号，控制电路开关管开通与关断。其控制结构框图如图5所示。

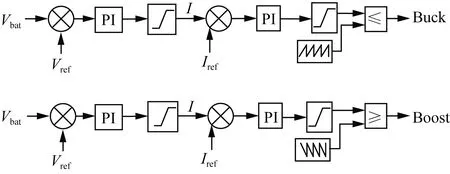
Vbat为电池电压；Vref为设定参考电压；Iref为设定参考电流；Buck为 降压斩波信号；Boost为升压斩波信号图5 双向功率变换器DC-DC控制框图Fig.5 DC-DC control block diagram of bidirectional power converter

3 仿真结果分析

在MATLAB/Simulink仿真平台下搭建双向功率变换器模型，分别对传统电感解耦控制和改进型无电感解耦控制进行仿真，并将改进型后的控制策略分别用于单向充放电、双向恒流充放电，双向变流充放电三种不同充电模式，验证本文所提控制策略的可行性。仿真系统参数如表1所示。

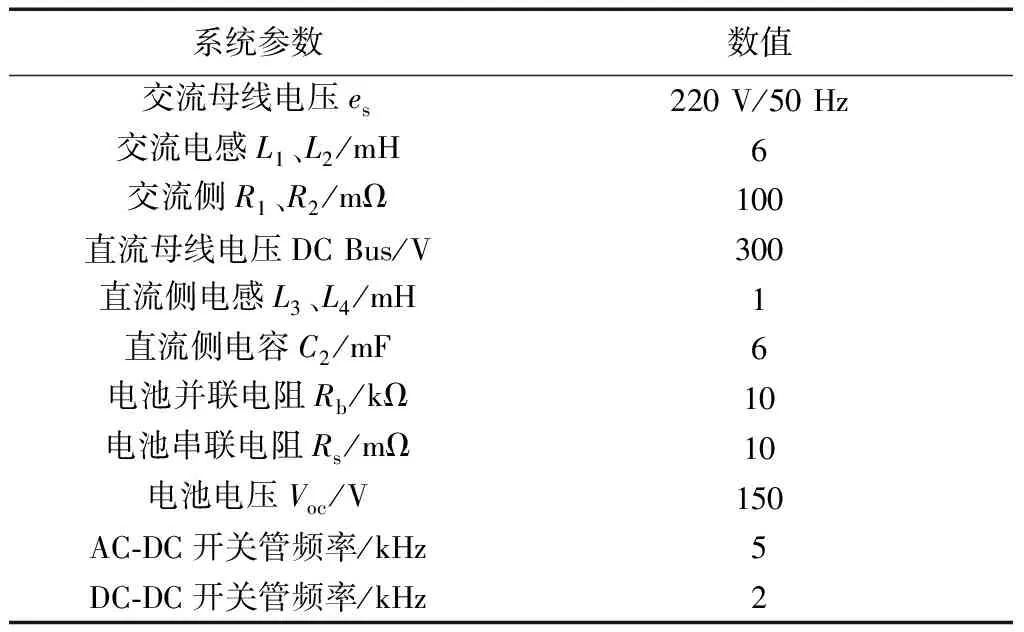
表1 系统参数Table 1 System parameters

3.1 电感解耦仿真

首先对传统电感解耦控制与改进型无电感解耦控制进行仿真，通过对比解耦后电流与解耦前参考电流，分析电感饱和对解耦的影响。

综上所述，当电流过大时，电感会产生饱和，造成解耦不充分，相比于传统电感解耦，改进型无电感解耦控制不含有电感项，采用积分模块避免了电感饱和造成的影响，有利于控制精度。

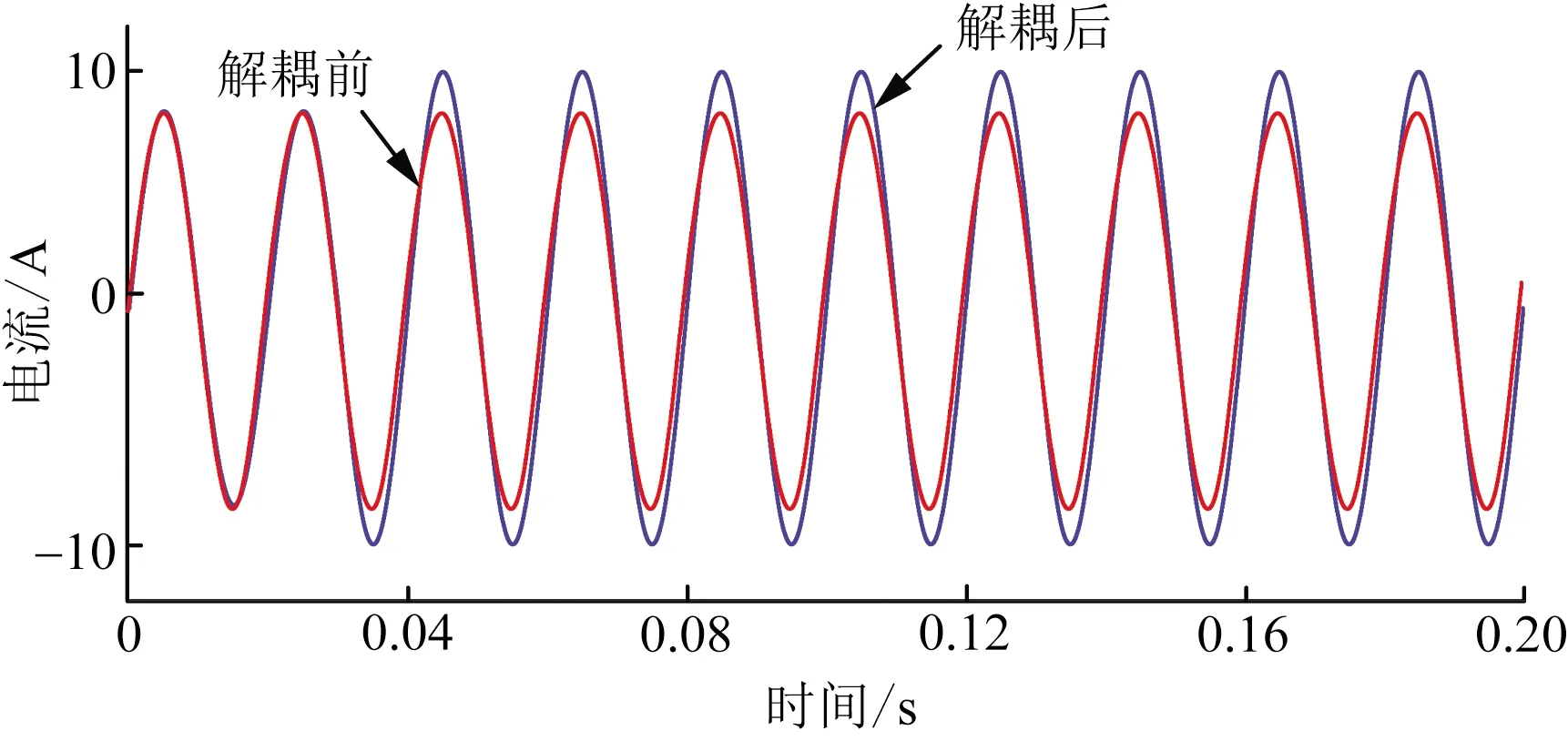
图6 改进型无电感解耦控制对比仿真图Fig.6 Simulation diagram of decoupling comparison under normal working conditions of power grid

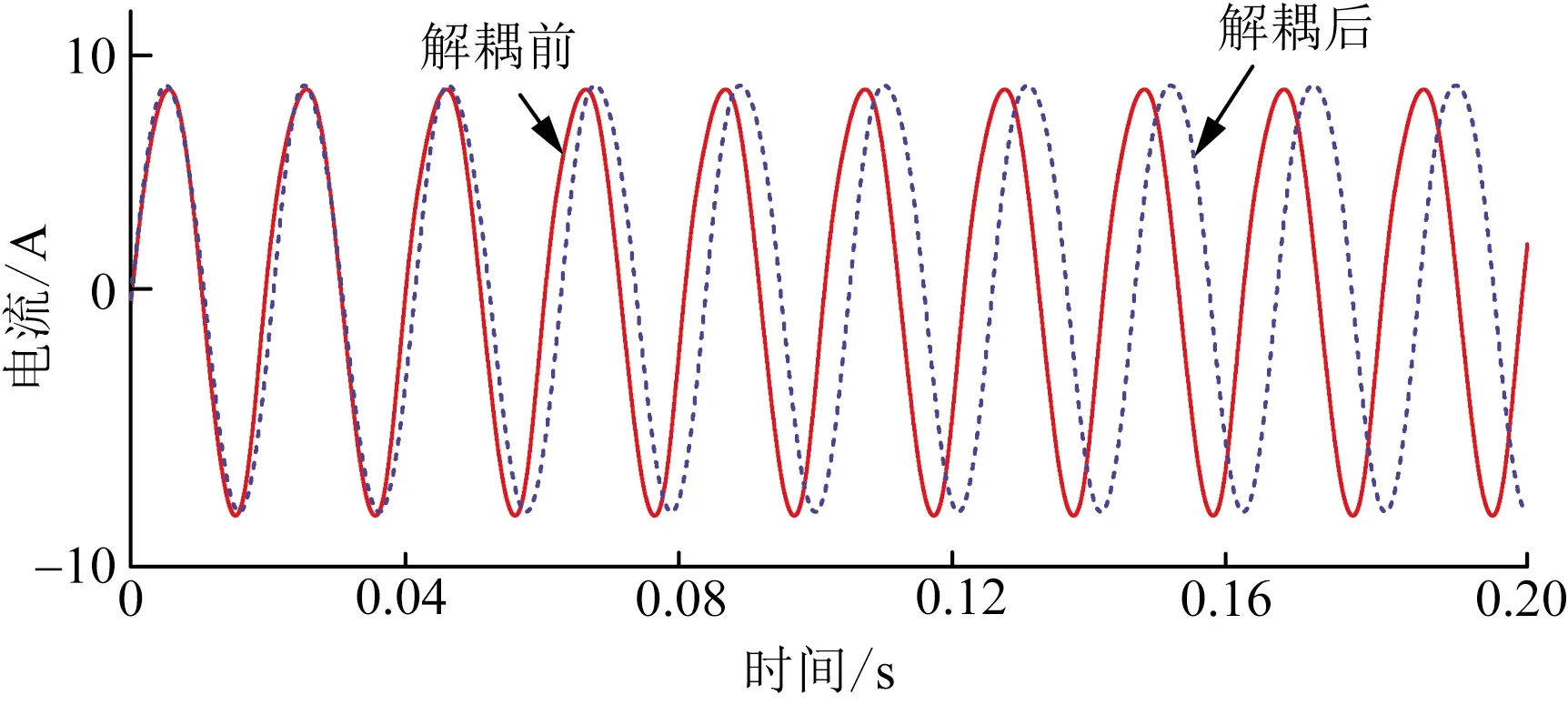
图7 传统有电感解耦控制对比仿真图Fig.7 Comparison simulation diagram of traditional inductive decoupling control

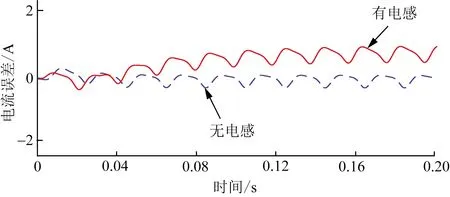
图8 两种控制误差对比仿真图Fig.8 Comparison simulation diagram of two control errors

3.2 单向充放电仿真

为了验证改进型无电感控制策略的可行性，通过单向充放电、双向充放电进行仿真验证。设定充放电电流为10 A，充放电时间为20 s,实现恒流充放电过程，电池冲放电流如图9(a)所示，电池内部充电时电流值为负，反之为正。充电过程中，双向功率变换器先进行整流，通过仿真结果可以看出在经过1 s超调后，电池以10 A的电流进行充电；放电过程中，电池直接放电，电池端不存在超调，以10 A的电流恒流放电。电池充放电时，电池两端电压大小如图9(b)所示，在充电状态下，经过20 s，电池电压从149 V上升至154 V；在放电状态下，负载电流在电池内阻上产生一定的压降，电池电压从149 V下降至146 V，并逐渐趋于缓和。电池初始SOC设定为50%充放电过程中电池荷电状态(state of charge，SOC)变换如图9(c)所示，经过20 s充电过程，电池SOC从50%提升至50.4%；放电过程中，电池荷电状态从50%下降至49.6%，完成放电全过程。图9(d)为单向充放电时，直流母线电压大小，充电状态下，经过1.5 s，直流母线电压达到300 V，且母线电压稳定在300 V；放电过程中，由于电池电压直接经升压斩波达到直流母线电压300 V,超调时间明显小于充电过程。

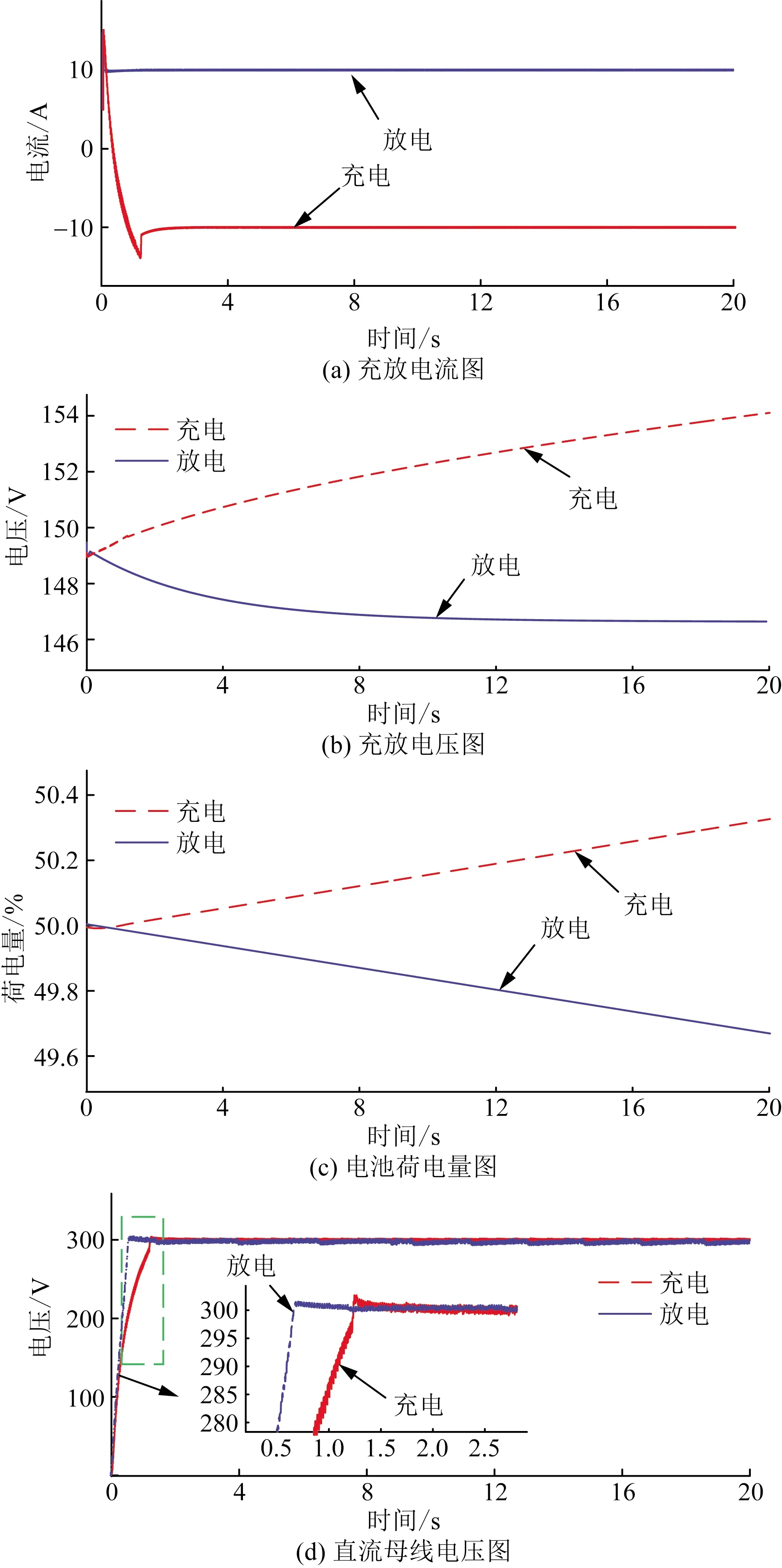
图9 单向充放电仿真图Fig.9 Simulation diagram of unidirectional charging and discharging

由上述分析可知，在单向充放电模式下，该控制策略能够实现电动汽车与电网的能量交换，对电池充放电电流进行控制，保证直流母线电压处于稳定状态，维持交流侧与直流侧功率平衡，提高传输效率。

3.3 双向充放电仿真

在双向充放电仿真中采用两种模式：双向恒流模式和双向变流模式。通过两种模式验证该控制策略的有效性。如图10(a)和图10(b)所示，为双向恒流充放电模式，在0～7 s时间内，双向功率变换器以10 A电流进行充电，电池两端电压从150 V上升至152 V，完成充电过程；在7～13 s时间内，双向功率变换器不进行充放电工作，充放电电流为0，由于电池内阻缘故，当停止充电时，电池两端电压开始逐渐跌落；在13～20 s时间内，双向功率变换器工作于放电状态，电池以10 A的电流大小进行放电，反馈给电网，电池两端电压由151 V开始回落。

图10(c)和图10(d)为双向变流充放电模式，在0～3 s内双向功率变换器以5 A的电流大小给电池充电，电池两端电压由150 V升至151 V,随后变换器充电电流升至10 A，在经过4 s后，电池两端电压升至152 V，增长速率更快，曲线斜率变大。在7～13 s内，充电电流为0，双向功率变换器无能量流动，电池内阻导致电池两端电压逐步下降，在13～15 s时间内，电池以5 A电流进行放电，变换器能量由电池端馈流给电网，15～20 s内，电池放电电流升至10 A，持续放电5 s,电池两端电压降至150 V。

图10(e)为双向充放电时电池SOC变化情况，从图10(e)中可以看出，充放电时电流大小不同，电池荷电量增长速率也不同，充电时，荷电量上升，放电时荷电量下降，由于仿真时长较短，荷电变化较小。

图10(f)为双向充放电过程中直流母线电压大小，充放电过程中直流母线电压始终维持在300 V,电压纹波控制在2%以内，误差为2 V。

由上述分析可得，在该控制策略下，功率变换器能实现恒流和变流充放电，通过调节充电电流大小，实现快充与慢充方式变换，在稳定直流母线电压的情况下，使电池达到深度充放电，延长电池使用寿命。

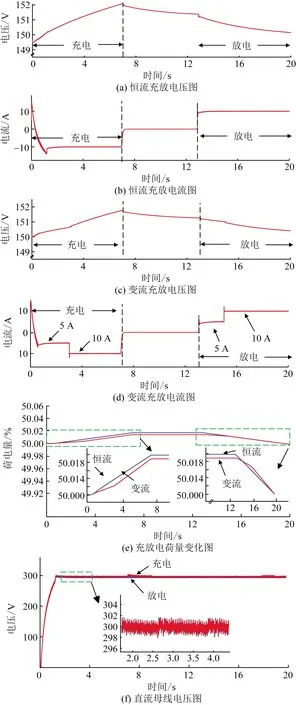
图10 双向充放电仿真图Fig.10 Two-way charge-discharge simulation diagram

4 实验结果分析

实验采用TI公司的TMS320F28335 DSP开发板进行控制策略实验验证，对比分析传统有电感解耦控制模式与改进型无电感解耦控制模式的输出电流波形，验证该控制策略可行性。

图11(a)为传统有电感解耦下的波形图，采样时间25 ms，幅值为每格500 mV。可以看出解耦后电流波形相比解耦前电流波形产生了一定延迟，相位发生变换，没有同步。这是由于电流过大，造成电感线圈饱和，导致解耦不充分引起的。图11(b)为改进型无电感解耦电流波形图，为了便于对比观察，将解耦后电流波形进行上移，分析可知解耦后的电流波形图与解耦前电流波形图同步，没有受到电感饱和的影响，相位未发生变化。

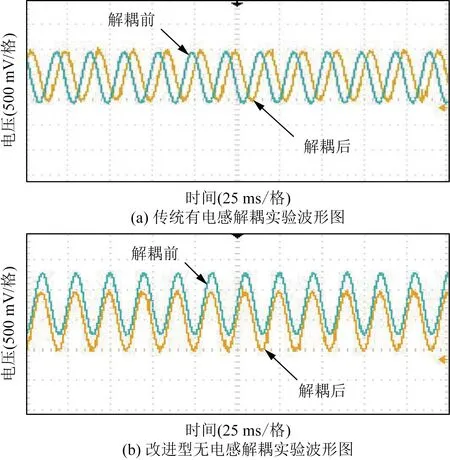
图11 解耦实验波形图Fig.11 Waveform of decoupling experiment

综合上述实验可以看出，采用无电感解耦的控制方法可以达到精确解耦，避免了由于电感线圈饱和造成的解耦不充分，提高了后续PWM控制的精度。

5 结论

针对车载双向功率变换器，提出一种改进型无电感解耦控制策略。通过SOGI发生器生成标准正交信号，用于坐标变换，代替传统延迟法构造，加快响应速度。采用改进型无电感解耦控制策略，避免了因电流过大造成电感饱引起的解耦不充分问题，提高了解耦精度。通过仿真与实验验证了该控制策略的可行性，能在单向充放电、双向恒流充放电、双向变流充放电，三种模式下，实现电网与电动汽车之间的能量交换，维持直流母线电压稳定，实现功率平衡，控制方法简单，效率高，便于数字信号处理器(digital signal processing，DSP)实现。